3、弹性地基梁理论
- 格式:ppt
- 大小:1.12 MB
- 文档页数:57




弹性地基梁法整体式平底板的平面尺寸远较厚度为大,可视为地基上的受力复杂的一块板。
目前工程实际仍用近似简化计算方法进行强度分析。
一般认为闸墩刚度较大,底板顺水流方向弯曲变形远较垂直水流方向小,假定顺水流方向地基反力呈直线分布,故常在垂直水流方向截取单宽板条进行内力计算。
按照不同的地基情况采用不同的底板应力计算方法。
相对密度Dr >0.5的砂土地基或粘性土地基,可采用弹性地基梁法。
相对密度Dr 0.5的砂土地基,因地基松软,底板刚度相对较大,变形容易得到调整,可以采用地基反力沿水流流向呈直线分布、垂直水流流向为均匀分布的反力直线分布法。
对小型水闸,则常采用倒置梁法。
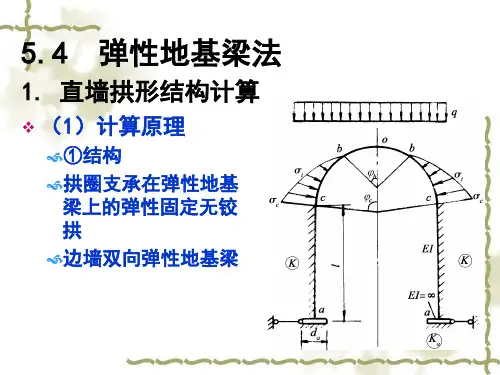
(一)弹性地基梁法该法认为底板和地基都是弹性体,底板变形和地基沉降协调一致,垂直水流方向地基反力不呈均匀分布(图1),据此计算地基反力和底板内力。
此法考虑了底板变形和地基沉降相协调,又计入边荷载的影响,比较合理,但计算比较复杂。
当采用弹性地基梁法分析水闸闸底板应力时,应考虑可压缩土层厚度T 与弹性地基梁半长L /2之比值的影响。
当L T 2小于0.25时,可按基床系数法(文克尔假定)计算;当L T 2大于2.0时,可按半无限深的弹性地基梁法计算;当2T /L 为0.25-2.0时,可按有限深的弹性地基梁计算。
弹性地基梁法计算地基反力和底板内力的具体步骤如下:(1)用偏心受压公式计算闸底纵向(顺水流方向)地基反力。
(2)在垂直水流方向截取单宽板条及墩条,计算板条及墩条上的不平衡剪力。
以闸门槽上游边缘为界,将底板分为上、下游两段,分别在两段的中央截取单宽板条及墩条进行分析,如图1(a )所示。
作用在板条及墩条上的力有:底板自重(q 1)、水重(q 2)、中墩重(G 1/b i )及缝墩重(G 2/b i ),中墩及缝墩重中(包括其上部结构及设备自重在内),在底板的底面有扬压力(q 3)及地基反力(q 4),见图1(b )所示。
图1作用在单宽板条上的荷载及地基反力示意图由于底板上的荷载在顺水流方向是有突变的,而地基反力是连续变化的,所以,作用在单宽板条及墩条上的力是不平衡的,即在板条及墩条的两侧必然作用有剪力Q 1及Q 2,并由Q 1及Q 2的差值来维持板条及墩条上力的平衡,差值ΔQ =Q 1-Q 2,称为不平衡剪力。

地下建筑结构第3章弹性地基梁理论
崔振东副教授IAEG, FICDM, FICCE cuizhendong@
中国矿业大学岩土工程研究所
3.3 按温克尔假定计算短梁z3.3.2 荷载引起的附加项
3.3.2 荷载引起的附加项(1)集中荷载P 引起的附加项
3.3.2 荷载引起的附加项(2)力矩荷载M 引起的附加项
3.3.2 荷载引起的附加项
(3)分布荷载q 引起的附加项
如视x 为常数,则d(x-u)=-d u
代入
a. 梁上有一段均布荷载的附加项
,0==du
dq q q
b. 梁上有一段三角形分布荷载的附加项
()3
4334,x x q du dq x u x x q q −Δ−=−−Δ=
c. 梁的全跨布满均布荷载的附加项
布满梁的全跨时,
当均布荷载q
=0,并且任一截面的坐标距
则x
3
x永远小于或等于x4。
d. 梁的全跨布满三角形荷载的附加项
当三角形荷载
=0,并且任一截面的坐标距
则x
3
x永远小于或等于
= =
(1)查双曲线三角函数K
=。

第 1 章绪论1、地下建筑结构是修建在地层中的建筑物。
它可以分为两大类:一类是修建在土层中的;一类是修建在岩层中的;广义上讲,任何结构物都是修建在相应的介质中的2、地下建筑结构的作用(1)地下建筑结构,即埋置于地层内部的结构。
修建地下建筑物时,首先按照使用要求在地层中挖掘洞室,然后沿洞室周边修建永久性支护结构——即衬砌结构。
而内部结构与地面建筑的设计基本相同(2)作用:衬砌结构主要是起承重和围护两方面的作用。
承重,即承受岩土体压力、结构自重以及其它荷载的作用;围护,即防止岩土体风化、坍塌、防水、防潮等。
3、地下建筑与地面建筑结构的区别(1)计算理论、设计和施工方法(2)地下建筑结构所承受的荷载比地面结构复杂。
(3)地下建筑结构埋置于地下,其周围的岩土体不仅作为荷载作用于地下建筑结构上,而且约束着结构的移动和变形。
所以,在地下建筑结构设计中除了要计算因素多变的岩土体压力之外,还要考虑地下结构与周围岩土体的共同作用。
这一点乃是地下建筑结构在计算理论上与地面建筑结构最主要的差别。
第 2 章地下建筑结构的荷载1、掌握地下建筑结构所承受的荷载类型及其组合原则。
按存在状态可分为:静荷载、动荷载和活荷载等静荷载:又称恒载。
是指长期作用在结构上且大小、方向和作用点不变的荷载,如结构自重、岩土体压力和地下水压力等;动荷载:要求具有一定防护能力的地下建筑物,需考虑原子武器和常规武器(炸弹、火箭)爆炸冲击波压力荷载,这是瞬时作用的动荷载;在抗震区进行地下结构设计时,应计算地震波作用下的动荷载作用活荷载:是指在结构物施工和使用期间可能存在的变动荷载,其大小和作用位置都可能变化,如地下建筑物内部的楼地面荷载(人群物件和设备重量)、吊车荷载、落石荷载等。
地面附近的堆积物和车辆对地下结构作用的荷载以及施工安装过程中的临时性荷载其它荷载:使结构产生内力和变形的各种因素中,除有以上主要荷载的作用外,通常还有:混凝土材料收缩(包括早期混凝土的凝缩与日后的干缩)受到约束而产生的内力;各种荷载对结构可能不是同时作用,需进行最不利情况的组合。



弹性地基梁计算模型研究一、本文概述《弹性地基梁计算模型研究》一文旨在深入探讨弹性地基梁的计算模型及其在实际工程中的应用。
文章首先介绍了弹性地基梁的基本概念,阐述了其在土木工程领域的重要性。
随后,文章综述了国内外关于弹性地基梁计算模型的研究现状和发展趋势,分析了现有模型的优缺点,指出了研究中存在的问题和挑战。
在此基础上,文章提出了一种新的弹性地基梁计算模型,该模型综合考虑了地基的弹性特性、梁的变形特性和外部荷载的作用,能够更准确地模拟实际工程中的弹性地基梁行为。
为了验证新模型的准确性和有效性,文章还进行了一系列的数值计算和实验验证,将新模型与现有模型进行了对比分析,得出了有益的结论。
文章总结了研究成果,展望了未来的研究方向和应用前景,为土木工程领域的相关研究提供了有益的参考和借鉴。
二、弹性地基梁基本理论弹性地基梁,也称为温克尔地基梁,是一种重要的工程结构形式,广泛应用于各种土木工程领域。
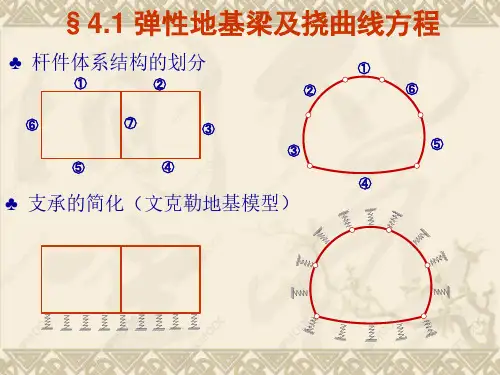
其基本理论建立在温克尔假设之上,即地基上任一点的反力与该点的沉降量成正比,而与其他点的沉降无关。
这种假设简化了地基的复杂性,使得弹性地基梁的分析和计算成为可能。
弹性地基梁的基本理论包括梁的平衡微分方程、变形协调方程以及地基反力方程。
平衡微分方程描述了梁在受到外力作用时的平衡状态,变形协调方程则描述了梁的变形与地基沉降之间的关系,而地基反力方程则根据温克尔假设表达了地基对梁的反力。
在弹性地基梁的分析中,通常采用有限元法、差分法或解析法等方法进行求解。
这些方法可以求解出梁的位移、应力、应变以及地基反力等关键参数,为工程设计和施工提供重要依据。
然而,弹性地基梁理论也存在一定的局限性。
由于温克尔假设忽略了地基的剪切变形和连续性,因此在实际应用中可能会产生一定的误差。
为了更准确地模拟地基的实际行为,研究者们提出了各种改进的地基模型,如双参数地基模型、非线性地基模型等。
这些模型在保留弹性地基梁理论优点的通过引入更多的参数或考虑非线性因素,提高了理论的适用性和准确性。