d4y
qx o
,即得对应齐次微分方程:
EI ky 0
dx 4
(3.7)
由微分方程理论知,上述方程的通解由四个线性无关的特解组合而成。 K
EI
或 4 K cos i sin
EI
由复数开方根公式得:
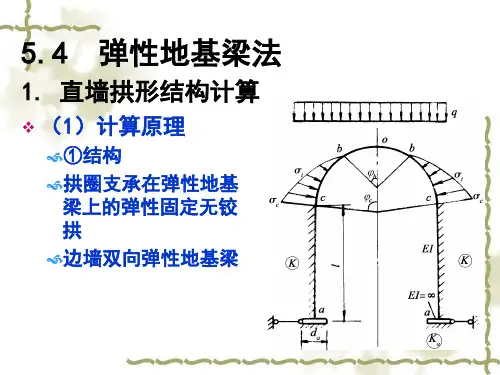
优点: 可以考虑梁本身的实际弹性变形,消除了反力直 线分布假设中的缺点。
缺点:
没有反映地基的变形连续性,故温克尔假设 不能全面反映地基梁的实际情况。
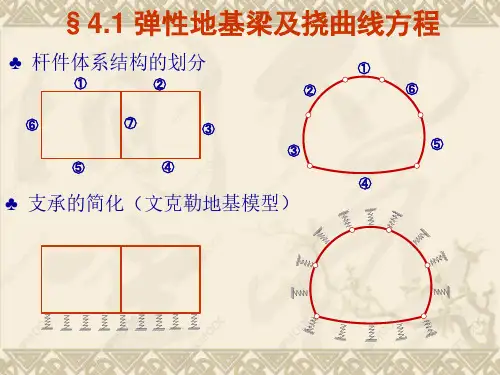
2. 半无限体弹性地基模型 假设:
把地基看作一个均质、连续、弹性的半无限体(所谓 半无限体是指占据整个空间下半部的物体,即上表面 是一个平面,并向四周和向下方无限延伸的物体)。
(二)用初参数表示积分常数
如图3.4所示,梁左端的四个边界 条件(初参数)为
图3.4 弹性地基梁作用的初参数
y x o yo
x o o
M x o Mo
Q x o Qo
(3.13)
将上式代入式(3.12),解出 积分常数得:
3. 初参数解
B1 yo
2. 对应齐次微分方程的通解
由上式(3.8),分别令时k=1,2,3时,即可得四个线性无关的特解,将其进行 组合并引入四个积分常数,即得齐次微分方程式(3.7)的通解;
y ex A1 cosx A2 sin x ex A3 cosx A4 sin x (3.10)
Y1 = e( + i)x, 由叠加原理, 知
Y2 = e( – i)x
y1
Y1
2
Y2
ex cos x
y2
Y1
Y2 2i