平口单峰函数(野猪)

2019-2020年高中数学第1讲优穴二单峰函数练习新人教A版选修、基础达标1. 关于单峰函数，有下列说法：①在区间［a, b］上的单峰函数就是只有一个极大值点的函数;②在区间［a，b］上的单调函数不是单峰函数；③对有关因素的最佳组合进行选择，这样的问题称为优选问题;④在试验范围内具有极值性的问题称为具有单峰性的问题其中正确的个数有()A.0个B.1个C.2个D.3个解析①②④错误，只有③正确•答案B2. 下列函数在区间［—10, 10］上是单峰函数的为()1A. y=B.y = cos xx + 1B.[ —1, 1]C. 12D.12解析 因为2为好点，舍去区间［3 , 4］，存优范围为［1 , 3). 答案［1 , 3) 5.在粉笔加工设计中，每支粉笔都要丢掉一段一定长的粉笔头，单就这一点来说，愈长愈好，但太长了，使用起来既不方便，也容易折断，每断一次，必然多浪费一个粉笔 头，反而不合适，因而就出现了“粉笔多长最合适”的问题，技术员王工在长度为 10cm 至15 cm 范围内经过多次尝试，最后发现 12 cm 长的粉笔最合适.根据上述描述，请回答下列问题：(1)这个问题的可控因素是 ___________ ； ⑵这个问题的最佳点是 ___________ .解析 (1)这个问题是优选问题.这个问题是寻找粉笔的合适长度，因此可控因素是粉笔 的长度. ⑵本题是寻找粉笔的合适长度，因此最佳点就是最合适的粉笔长度，即 12 cm.(1)粉笔的长度 (2)12 cmt >0,则函数y = t —： + 1的最佳点为2t — 4t + 1 1y = t= t +1—4>— 2（t >0）,当且仅当t = 1时，y min =— 2. 答案 1 、能力提升 7.说出下列优选问题中的可控因素 .① 购房者在选择适合自己的房屋时，会从房屋的位置、价格等不同特性进行对比，从中 选择合适的房子.② 调配葡萄酒时，需用两种原酒调配而成，如由赤霞珠、梅鹿辄组合成的干红葡萄酒， 经过多次试验，确定两种原酒的最佳比例③ 做馒头，碱放少了馒头会酸，碱放多了馒头会变黄、变绿且带碱味，碱放多少才合适 呢？④ 为了加强钢的强度，要在钢中加入碳，加入太多太少都不好，究竟加入多少碳，钢才 能达到最咼强度呢？解(1)中的可控因素是位置、价格等；⑵ 两种原酒的比例；(3)加入碱的量； ⑷ 加入碳的量.___ 328. 已知函数 f (x ) = x + 3ax + 3x + 1.答案 6.已知 解析⑴若f(x)在［0 ,+^)上单调，求a的取值范围•(2)若g(x) = f(x) —3x在［—1, 4］上是单峰函数，求a的取值范围•2 1解⑴由f '(x) = 3x + 6ax+ 3》0对任意x>0 恒成立，得—2a<x+-?x —2a<2? a>— 1.(2)由g'(x) = f '(x) —3= 3x2+ 6ax= 3x( x+ 2a)，由g'(x) = 0 可得x= 0 或x=—2a.•••0€ ( —1, 4)，所以一2a?( —1, 4),1•••—2a<—1 或一2a>4,即卩a>㊁或a w—2.一 1 、故a的取值范围是(一a,—2］U (2，+^ .9. 有甲、乙两种商品，经营销售这两种商品所能获得的利润依次为P万元和Q万元.它们与投入资金x万元的关系有经验公式P= 5x, Q= 5、x.现有3万元资金投入经营甲、乙两种商品，为获得最大利润，则对甲、乙两种商品的资金投入分别为多少？并说明此优选问题是否具有单峰性质.解设对甲种商品投资x万元，则乙种商品投资为(3 —x)万元，又设所获得的利润总额为y 万元，由题意有y = ~x + 5 -3—x, x€ ［0 , 3］.令3—x = t，贝U x= 3—t2, t € ［0 , 3］，从而y = 5(3 —12)+ 5t = —g t—+ 20, t € ［0, 3］.当t = ［0, ,3］时，y max21 9 3 3 9=20.即知x=3—4=4 3—x=3一4=j.因此，为获得最大利润，对甲、乙两种商品的资金投入应分别为0.75万元和2.25万元，获得的最大利润为1.05万元.这个优选问题中的目标函数，经过换元之后为有最大值的二次函数，而二次函数为单峰函数，因此这个优选问题具有单峰性质三、探究与创新10. 证明：若目标函数为单峰函数，则最佳点与好点必在差点的同侧证明下面仅对单峰函数f (x)上凸的情形进行证明.设点c为［a, b］上的单峰函数f (x)的最大值点，m, n €［a, b］，且f( n) >f (n).因为f (x)(1)设n€［a, c］，如图，因为为单峰函数，所以f (x)在［a, c］递增，在［c, b］递减.m€[n, b].因为n€[a, c]，所以c€[n, b].因此，点m c在点n的右侧.⑵设n€[ c, b].因为m n €[ a, b]，且f (nj > f ( n)，所以n?[ n, b]，即m^[a, n].因为n€[c, b]，所以c€[a, n].因此，点m c在点n的左侧.由⑴(2)可知点m c始终在点n的同侧. 2019-2020年高中数学第1讲优穴五其他几种常用的优穴一练习新人教A一、基础达标1. 下列说法中，正确的个数为()①分数法在确定下一个试点时，需要对前两个试点的试验结果进行比较；1②对分法、分数法、0.618法均做了2次试验后，才舍弃试验范围的3；③用对分法做试验较0.618法好，因为每次可以舍弃试验范围的一半；④若做一次试验，根据结果可以决定下次试验的方向，就可以用对分法A.1B.2C.3D.4解析①③④正确，所以正确答案有3个，选C.答案C2. 下列说法中，不正确的个数为()①影响盲人爬山法效果的因素为起点与步长；②盲人爬山法的原理就是单峰函数的最佳点与好点在差点的同侧；③盲人爬山法在实践中往往采取“两头大，中间小”，即先在各方向上用大步试探开始；④盲人爬山法应用于某些可变因素要调到某点，必须经过由小到大或由大到小的连续过程的问题.A.0B.1C.2D.3B.解析③应为“两头小，中间大”，而①②④正确，所以答案为答案B3. 用0.618法和对分法安排试验，找出蒸馒头时合适的放碱量，哪种方法更有效（）A.0.618法B.对分法C. 一样好D.无法确定解析对分法更简单，易操作•答案B4. 有一条1 000 m长的输电线路出现了故障，在线路的开始端A处有电，在末端B处没有电，现用对分法检查故障所在位置，则第二次检查点在（）A.500 m 处B.250 m 处C.750 m 处D.250 m 或750 m 处解析若在AB的中点测试有电，则第二次检查点为750 m处；若AB的中点检查没电，则第二次检查点为250 m处.答案D5. 用对分法进行试验，4次试验后精度为____________ .|1 4 1解析精度S 4= = ~.<2）16答案16. 用对分法寻找最佳点时，达到精度为0.01的要求至少需要_____________ 次试验.解析由2n三血？心7，•••至少需要7次.答案7二、能力提升7. 调试仪器中的可变电阻，可变电容常常采用的优选法为_______________ .答案盲人爬山法8. 看商品猜价格的具体规则：主持人出示一件物品，参与者每次估算出一个价格，主持人只能回答：“高了”、“低了”、“正确”.若猜中，则游戏结束，否则在规定时间内继续猜下去，直到猜中为止.若现在一个价格在范围为[1 000 , 2 000]（价格数为整数，单位为元）的商品，请你用对分法来猜.(1) 若第一次就能猜中，则这个商品的价格是多少？(2) 哪几个价格猜三次就可以猜到？1 500，故能解(1)由对分法知，每次都是取因素范围的中点值，第一次的中点值是次就猜中的价格是 1 500元.⑵第三次能猜中，即第三次取的试验点就是猜中的价格由第一次的中点值为 1 500，此时可得存优范围为［1 000，1 500］或［1 500，2 000］，第二次的中点值取上述两个范围内的中点值，即为 1 250或1 750，此时存优范围为［1000，1 250］，［1 250，1 500］，［1 500，1 750］，［1 750，2 000］中的任一个.故第三次的中点值可分别为 1 125，1 375，1 625，1 875，即猜三次就猜中的价格是 1 125元，1 375元，1 625元，1 875元中的一个.9. 某同学在借助计算器求“方程lg x = 2-x的近拟解(精确度为0.1) ”时，设f(x) = lg x+ x —2，算得f(1)<0 , f(2)>0 ;在以下过程中，他用“对分法”又取了4个x的值，计算了其函数值的正负，并得出判断，方程的近似解x-1.8，那么他取的x的4个值分别依次是_________ .解析••• f(1)<0 , f(2)>0 ,•••方程的根x € (1 , 2).1 + 2X1= — = 1.5，贝U f (1.5)<0，故方程的根x € (1.5 , 2).1 5 + 2X2= 2= 1.75，贝y f (1.75)<0，故方程的根x € (1.75 , 2).1.75 + 2X3= ~ = 1.875，贝U f (1.875)>0，故方程的根x € (1.75 , 1.875).1.75 + 1.875X4= = 1.812 5，贝U f(1.812 5)>0 ，故方程的根x€ (1.75 , 1.812 5).又|1.812 5 — 1.75|<0.1 ，故可把x-1.8作为其近似值答案 1.5 , 1.75 , 1.875 , 1.812 5三、探究与创新10. 程序设计中有一种折半查找检索算法，其原理与对分法类似，也有所不同，如查找范围［a, b］内某一值c(c€［a, b］, b> a)，且a, b, c都是正整数，先取m=，芦^ k式子［x］表示不超过x的最大整数)为试验点，比较c与m的大小，如果相等，则查找成功；如果c v m则查找范围为［a, n—1］;若c > m,则查找范围为［m^ 1, b］，按此下去,直至c= m为止.每比较一次称为查找一次，设找到c的查找总次数记为f (c).此时查找的次数为n 次，如f (1) = f (2n — 1) = n ,即卩f (x ) max = n .⑴若查找范围是［1 , 7］，求f ⑷，f (3) , f (7)的值.⑵ 设x € ［1 , 2n - 1］，你能得出f (x )的最大值与最小值吗?解⑴易知查找范围是［1，7］时，第一个试验点m r- ［4］ = 4,所以f (4) =1.求f (3)，由于第一次比较后的查找范围为 ［1 , 3］，接着第二个试验点为 呼2V 3,同理查找f (7)的查找范围依次为［1 , 7］ , ［5 , 7］ , ［7 , 7］，在［7 , 7］中找得第三个试验点为7,所以f (7) = 3.易知第一次查找的范围内的个数值为2n — 1个,第二次查找的范围是［1 , 2n — 1— 1］或［2 n — 1+ 1 , 2n — 1］，不论哪种情况，此时范围内的个 数为2n —1 — 1个.即查找一次，如果不成功，则查找范围变为原来的一半减半个 第三次查找的范围的个数是2n —2— 1个.最后到了 22— 1 = 3个时，比如此时存优范围是 ［1 , 3］，取中值m = 2,考虑查找次数最大 值的情况，再得到存优范围［1 , 1］或［3 , 3］.所以此时范围为［3 , 3］.由第三个试验点值为 73+ 3 I 2=［3］ = 3，查找结束，所以 f (3) = 3.(2)由(1)知，当x =1 +( 2n — 1)2=2n — 1 时, f (x )取最小值，此时 f ( X ) min = 1.再对范围为［1 , 1］或［3 , 3］再取一次就是.1C.y= 2xD.y = §x1 * 3- x2—3x解析根据单峰函数的定义及规定知只有y = 2x在区间［—10, 10］上为单峰函数.答案C3. 已知f(x) = 2x3—6x2+ m在区间［—3 , 2］上是单峰函数，则下列哪个存优范围最小( )A.[ —2, 2]2解析由f '( x) = 6x —12x= 0，知X1= 0, X2= 2,所以最佳点是x= 0，所以C选项排除，由A, B, D的区间范围可知D的范围最小，故选D项.答案D4. 若某单峰函数的存优范围是［1 , 4］，现在区间［1 , 4］上任取两点2, 3，通过比较，2与3相比，2是好点，则此时的存优范围是 _____________ .此时查找的次数为n次，如f(1) = f (2n—1) = n,即卩f (x) max= n.。

2.函数f(x)的图象:如下图所示:
-2-
冲A专题(1) 含绝对值的函数
知识提要
知识提要
专题考点
二、已知y=|f(x)-(kx+b)|在区间x∈[s,t]上的最大值为M,则M的最小
值是
.
这里仅通过类比或数形结合进行理解.
1.多点控制:|f(x)|在x∈[s,t]上的最大值的最小值问题(端点或切比雪
式为|x-t|≤1-tx2,即 tx2-1≤x-t≤1-tx2,
+1
1
且
t≥,
2 +1
+1
2+1
t∈[-1,
].
2
பைடு நூலகம்
化简得 t≤
解得
-7-
冲A专题(1) 含绝对值的函数
知识提要
专题考点
专题考点
3.(2019年6月浙江学考)已知f(x)是定义在R上的偶函数,且在[0,+∞)
上单调递增.若对任意x∈R,不等式f(a+|x-b|)≥f(|x|-2|x-1|)(a,b∈R)
冲A专题(1)
含绝对值的函数
-1-
冲A专题(1) 含绝对值的函数
知识提要
知识提要
专题考点
一、绝对值的意义
1.绝对值函数的代数表达:f(x)=|x-a|=
-, ≥ ,
-, < .
一般解决绝对值问题,常规方法是采用分类讨论去绝对值,比较适
合大题的解答;对选择填空,可采用几何意义或两边夹逼近的思想.
则f(x)≤4恒成立⇔M≤4.
(i)当a≤0时,由(2)可知,
对于任意的x∈[-1,1],f(x)≤a2-a+2恒成立,
所以M=a2-a+2.

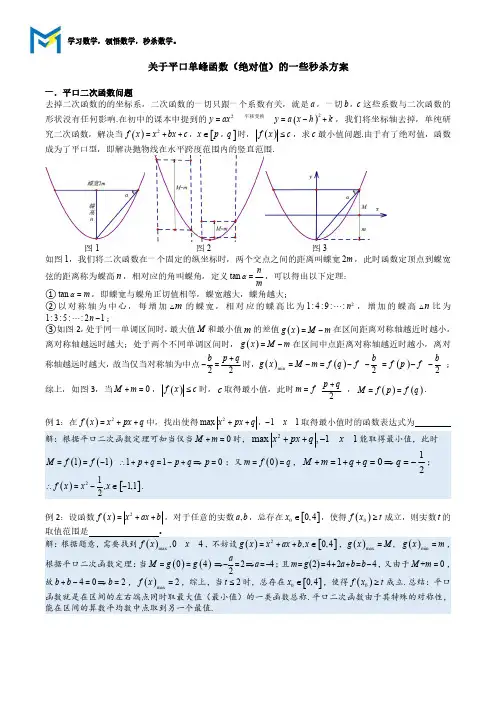
关于平口单峰函数（绝对值）的一些秒杀方案一．平口二次函数问题去掉二次函数的的坐标系，二次函数的一切只跟一个系数有关，就是a ，一切b c ，这些系数与二次函数的形状没有任何影响.在初中的课本中提到的()22y ax y a x h k 平移变换==-+，我们将坐标轴去掉，单纯研究二次函数，解决当()[]2f x x bx c x p q ，，=++Î时，()f x c £，求c 最小值问题.由于有了绝对值，函数成为了平口型，即解决抛物线在水平跨度范围内的竖直范围.图1图2图3如图1，我们将二次函数在一个固定的纵坐标时，两个交点之间的距离叫蝶宽2m ，此时函数定顶点到蝶宽弦的距离称为蝶高n ，相对应的角叫蝶角，定义tan nma =，可以得出以下定理：①tan m a =，即蝶宽与蝶角正切值相等，蝶宽越大，蝶角越大；②以对称轴为中心，每增加m 的蝶宽，相对应的蝶高比为21:4:9::n ，增加的蝶高n 比为1:3:5::21n -；③如图2，处于同一单调区间时，最大值M 和最小值m 的差值()g x M m =-在区间距离对称轴越近时越小，离对称轴越远时越大；处于两个不同单调区间时，()g x M m =-在区间中点距离对称轴越近时越小，离对称轴越远时越大，故当仅当对称轴为中点22b p q +-=时，()()()min 22b bg x M m f q f f p f =-=--=--；综上，如图3，当0M m +=，()f x c £时，c 取得最小值，此时2p qm f+=，()()M f p f q ==.例1：在()2f x x px q =++中，找出使得2max 11x px q x ，++-取得最小值时的函数表达式为解：根据平口二次函数定理可知当仅当0M m +=时，2max ,11x px q x ++-能取得最小值，此时()()11M f f ==-110p q p q p \++=-+Þ=；又()0m f q ==，1102M m q q q +=++=Þ=-；()[]21,1,12f x x x \=-Î-.例2：设函数()2f x x ax b =++，对于任意的实数,a b ，总存在[]00,4x Î，使得()0f x t ³成立，则实数t 的取值范围是。

构造“平口单峰”函数解决一些恼人的“切比雪夫最佳逼近直线”吴剑（野猪）1、1()42,(,)x x f x a b a b R +=+⋅+∈,若对任意的1[0,1],()2x f x ∈恒成立，则b =_______ 2、设函数4()||,f x ax x=−若*a R ∀∈总0[1,4]x ∃∈,使得0()f x m ,则实数m 的取值范围是_______ 3、设函数()||,,f x x ax b a b R =−−∈，若,a b R ∀∈，总0[0,4]x ∃∈,使得0()f x m 成立，则实数m 的取值范围为________4、已知函数2()||f x x ax b =++在区间[0,]x c ∈内的最大值为,(,,0M a b R c ∈>为常数)，且存在实数,a b 使得M 的最小值为2，则________a b c ++=5、已知2()(4)3f x x a x a =+−+−,[0,4]a ∀∈,均存在0[0,2]x ∈使得0|()|f x t 成立，则t的取值范围是______ 6、已知函数2()||f x ax b x=−−,若*,a b R ∀∈,总存在0[1,2]x ∈,使得0()f x m 成立，则实数m 的取值范围_______7、设函数2()||f x x ax b =++,若*,a b R ∀∈,总存在0[0,4]x ∈使得0()f x m 成立，则实数m 的取值范围是_______ 8、已知函数1()||f x x ax b x=+−−,当1[,2]2x ∈时设()f x 的最大值为(,)M a b ，则(,)M a b 的最小值为_______9、函数2()f x x px q =++中，找出使得2||,[1,1]max x px q x ++∈−取得最小值时的函数表达式10、（09湖北压轴）在R 上定义运算1:()()4(,3p q p c q b bc b c ⊗⊗=−−−+为常数)，记21()2f x x c =−2()2f x x b =−,x R ∈,令12()()()f x f x f x =⊗记()|()|,[1,1]g x f x x '=∈−的最大值为M 若M k 对任意的,b c 恒成立，试求k 的最大值 11、()ln(1),[0,1]f x x ax b x =+++∈,对任意的,a b R ∈,求|()|f x 的最大值的最小值 引理：若)(x f 为],[n m 上的连续单峰函数，且0),()(x n f m f =为极值点，则当b k ,变化时，b kx x f x g −−=)()(的最大值的最小值为2)()(0x f n f −.当且仅当2)()(,00x f n f b k +==时取得.这个引理的图像感受十分明显，但考虑到我也不是一个随便的人，还是写点废话证明一下 不妨以0(,)m x 上单调递减，0(,)x n 上单调递增为例：如图下面用反证法证明,km b kn b ++均等于0()()2f n f x +(1) 若两者其一小于0()()2f n f x +,不妨设0()()2f n f x kn b ++<此时0()()()()2f n f x f n kn b −−+>，矛盾(2) 若00()()()(),22f n f x f n f x km b kn b ++++>或00()()()(),22f n f x f n f x km b kn b+++>+ 则有00()()2f n f x kx b ++>此时000()()()2f n f x kx f x −−>矛盾所以0()()2f n f x km b kn b ++=+=,引理得证例题1、题目8、已知函数b ax xx x f −−+=1)(，当]2,21[∈x 时，设)(x f 的最大值为),(b a M ，则),(b a M 的最小值为 . 方法①：惊喜的发现xx 1+当]2,21[∈x 时已经是“平口单峰”函数，极值点为1，好幸运，所以),(b a M 的最小值为4122-221=+. 方法②：令)}2(),1(),21(max{),(f f f b a M t ==，即}2125,225,2max{),(b a b a b a b a M t −−−−+−==，则 b a t b a t b a t −−≥−−≥+−≥2125,225,2，所以 b a t b a t b a t 252,225,3366−−≥−−≥+−≥，所以2325656=+−≥t .所以41≥t .所以),(b a M 的最小值为41.例题2、题目7、设函数2()||f x x ax b =++,若*,a b R ∀∈,总存在0[0,4]x ∈使得0()f x m 成立，则实数m 的取值范围是_______解析：现在我们希望看到绝对值里面是一个“平口单峰”函数与一个一次函数，其实一次函数都是酱油，系数丑与不丑无所谓，所以可以考虑给2x 配凑一个一次式，使得2x x λ+成为[0,4]上的“平口单峰”函数，那么很明显，由0，4函数值相等可以求出4λ=−2()|4(4)|,f x x x a x b =−+++()f x 的最大值的最小值为0(4)22−−= 所以2m也可以顺便得到(4)0,2a b −+=−= 例题3、题目6：已知函数2()||f x ax b x=−−,若*,a b R ∀∈,总存在0[1,2]x ∈,使得0()f x m 成立，则实数m 的取值范围_______分析：（大神）很明显，我们需要给2x凑一个一次式，使得2x x λ+为[1,2]上的“平口单峰”函数。

平口单峰函数之倍角界定法满分秘籍：二倍角最值界定21cos cos 2+=αα，22cos 2cos 222cos 2cos 2)(2c a b a c a b a c bx ax x f +++≤+++=++=αααα，往往0220=+=ca b ，时，取得最值，这个方法通常在一些选填甚至解答压轴题中给你一种秒得很爽的感觉.例题1：设函数()2f x x ax b =++，对于任意的实数,a b ，总存在[]004x ，Î，使得()0f x t ³成立，则实数t 的取值范围是 ．例题2：（2018•呼和浩特期中）设函数(),,,f x ax b a b R -?若对于任意的实数,a b 总存在实数[]004x ，Î，使得()0f x m ³成立，则实数m 的取值范围为 ．例题3：已知函数()2f x x ax b=++，[]01x ∈，，若()f x 的最大值是M ，则M 的最小值是 ．满分秘籍：三倍角最值界定ααααααααααααα322sin 4sin 3sin )sin 21(cos sin 2sin 2cos cos 2sin )2sin(3sin -=-+=+=+=； αααααααααααααcos 3cos 4cos sin 2cos )1cos 2(sin 2sin cos 2cos )2cos(3cos 322-=--=-=+=；由此得到降幂公式：43cos cos 3cos 43sin sin 3sin 33αααααα+=-=， 当][m m x ，-∈时，可以设])0[(cos παα，∈=m x ，当]2[m m x ，-∈时，可以设])320[(cos παα，∈=m x ，以此类推；33|cos3+(+)cos +||cos3|+|(+)cos |+||4444a a a a b c b c αααα≤，往往0043==+c a b ，时取得最值.当ααααcos )3(2cos 3cos )(a c b a f +++=，且030>+>a c a ，，则0≤b 时，)()(min παf f =，当0≥b 时，)0()(max f f =α.例题1：已知函数 ()328f x x ax bx =--，是否存在任意实数a b 、，使得()2f x ≤对任意的[]11x ∈-，恒成立，若存在，求出a b 、，若不存在，说明理由．例题2：（2019•广东模拟）已知34a ≥-，0b ≥，函数3()f x x ax b =++，11x -≤≤，设|()|f x 的最大值为M ，且对任意的实数a ，b 恒有M K ≥成立，则实数K 的最大值为( ) A ．4B ．2C ．12D ．14例3：（2020•武汉3月调研）如果关于x 的不等式0123≥+-ax x 在]11[，-恒成立，则实数a 的取值范围是（ ）A ．0≤aB ．1≤aC ．2≤aD ．2233≤a例 4.（2019•武汉模拟）已知函数3()f x x ax b =++定义域为[12]-，，记|()|f x 的最大值为M ，则M 的最小值为( )A ．4B ．3C ．2D222例38.（2016•天津）设函数3()(1)f x x ax b =---，x R ∈，其中a ，b R ∈． （1）求()f x 的单调区间；（2）若()f x 存在极值点0x ，且10()()f x f x =，其中10x x ≠，求证：1023x x +=； （3）设0a >，函数()|()|g x f x =，求证：()g x 在区间[02]，上的最大值不小于14． 解：（1）函数3()(1)f x x ax b =---的导数为2()3(1)f x x a '=--， 当0a ≤时，()0f x '≥，()f x 在R 上递增；当0a >时，当1x >1x <()0f x '>，当11x <<+，()0f x '<，可得()f x 的增区间为(1-∞，，(1+)+∞，减区间为(11； （2）证明：0()0f x '=，可得203(1)x a -=，由322000000()(1)3(1)(1)(21)f x x x x b x x b =----=----，320000(32)(22)3(32)(1)f x x x x b -=-----2200000(1)(8896)(1)(21)x x x b x x b =---+-=----， 即为001(32)()()f x f x f x -==，即有0132x x -=，即为1023x x +=； （3）法一：证明：要证()g x 在区间[02]，上的最大值不小于14，只需证在[02]，上存在1x ，2x ，使得 121()()2f x f x -≥．当3a ≥时，()f x 在[0，2]递减，由(2)f 12a b =--，(0)1f b =--，得(0)(2)f f -12242a =-≥>，成立；当03a <<时，3(1((1f a b a b =--=+a b =-，3(1(1f a b a b =-+--a b =-， (2)f 12a b =--，(0)1f b =--，(2)f (0)22f a -=-，若304a <≤时，1(2)(0)222f f a -=-≥成立；若34a >时，1(1(12f f -=成立．综上可得，()g x 在区间[02]，上的最大值不小于14．法二平口单峰：根据第二问的结论，先构造()()()1121f x f x f -++=证明三次函数的对称中心为()()1,1f ，。

305专题5 关于平口单峰函数（绝对值）的一些秒杀方案秒杀秘籍：第一讲 平口二次函数问题去掉二次函数的的坐标系，二次函数的一切只跟一个系数有关，就是a ，一切b c ，这些系数与二次函数的形状没有任何影响．在初中的课本中提到的()22y ax y a x h k 平移变换=揪揪揪揪井=-+，我们将坐标轴去掉，单纯研究二次函数，解决当()[]2f x x bx c x p q ，，=++?时，()f x c £，求c 最小值问题．由于有了绝对值，函数成为了平口型，即解决抛物线在水平跨度范围内的竖直范围．图1 图2 图3如图1，我们将二次函数在一个固定的纵坐标时，两个交点之间的距离叫蝶宽2m ，此时函数定顶点到蝶宽弦的距离称为蝶高n ，相对应的角叫蝶角，定义tan nma =，可以得出以下定理： ①tan m a =，即蝶宽与蝶角正切值相等，蝶宽越大，蝶角越大；①以对称轴为中心，每增加m D 的蝶宽，相对应的蝶高比为21:4:9::n L ，增加的蝶高n D 比为1:3:5::21n L -； ①如图2，处于同一单调区间时，最大值M 和最小值m 的差值()g x M m =-在区间距离对称轴越近时越小，离对称轴越远时越大；处于两个不同单调区间时，()g x M m =-在区间中点距离对称轴越近时越小，离对称轴越远时越大，故当仅当对称轴为中点22b p q+-=时，()()()min 22b b g x M m f q f f p f 骣骣琪琪=-=--=--琪琪桫桫； 综上，如图3，当0M m +=，()f x c £时，c 取得最小值，此时2p qm f 骣+琪=琪桫，()()M f p f q ==． 【例1】在()2f x x px q =++中，找出使得2max 11x px q x ，++-＃取得最小值时的函数表达式为 ．【例2】设函数()2f x x ax b =++，对于任意的实数,a b ，总存在[]00,4x Î，使得()0f x t ³成立，则实数t 的取值范围是 ．秒杀秘籍：第二讲 平口对勾函数问题对勾函数涉及极值偏移，算数平均数的中点的值不代表最值，()[],,af x x b x p q x =++?时，()f x c £，求c 最小值问题，根据平口二次函数的推论，可以知道是()()f p f q =，如图4，求出参数a 以后再根据())0f p fa +=确定参数b ．306定理：当仅当a pq =时，对勾函数在区间[],p q 才能构成平口对勾函数，()f x 去最小值时取到了[],p q 的几何平均数中点．图4【例3】（2018•台州期末）已知()1f x x ax b x =+--，当1,22x 轾Î犏犏臌时，设()f x 的最大值为(),M a b ，则(),M a b 最小值为 ．【例4】（2018•青浦二模）设函数()2f x ax b x=--，对于任意的实数,a b ，总存在[]01,2x Î，使得()0f x m ³成立，则实数m 的取值范围是 ．秒杀秘籍：平口三次函数问题三次函数涉及到双峰问题，我们需要在给定的定义域内构造出单峰三次函数（即部分图像，通常是极大值到极大值等值点这一段），如下图，若[]12x ∈-，，我们可在此区间构造单峰函数．【例5】（2019•武汉调研）已知函数()3f x x ax b =++的定义域为[1,2]-，记()f x 的最大值为M ，则M 的最小值为（ ） A ．4B ．3C ．2D ．3秒杀秘籍：第三讲 关于平口函数的万能招数所有的平口函数()y f x =一定满足一个共性：出现求()maxmin f x ，[],x p q Î时，一定为平口函数，若()y f x =有一个极值点，也叫平口单峰函数，若()maxf x M =，()minf x m =，()()0f p f q M m ì=ïíï+=î此为平口单峰函数的万能招数．既然如此，再来几道题，都可以直接秒杀了．建议大家边写题边拍一下参考答案给的解法，对比一下，这种类型题能减少讨论是最好的．307【例6】（2018•呼和浩特期中）设函数(),,,f x x ax b a b R -?若对于任意的实数,a b 总存在实数[]00,4x Î，使得()0f x m ³成立，则实数m 的取值范围为 ．【例7】（2018•秋杭州期中）已知()ln f x x ax b =--，对于任意的0a <，b R Î，都存在[]01,x m Î使得()01f x ³成立，则实数m 的取值范围为 ．【例8】求()[]min max ln 101x ax b x a b R ，，、+++挝．下面给出一个平口单峰函数的解答题证明过程：若函数()f x 在区间[],p q 为连续的单峰函数，且()()f p f q =，此函数为平口单峰函数，0x 为其极值点．秒杀秘籍:()()max g x f x ax b =++的最小值为()()02f p f x -，当仅当0a =，()()02f p f x b +=-时取得．【例9】（2018•台州月考）已知函数()1f x x ax b x =+--，当122x ⎡⎤∈⎢⎥⎣⎦，时，设()f x 的最大值为()M a b ，，则()M a b ，的最小值是（ ）A ．2B ．21C ．4D ．41 秒杀秘籍：第四讲 构造平口函数若题目给的基本函数为非“平口单峰”，则我们需要构造“平口单峰”， 此处注意：构造平口单峰函数的后边应为一次函数．下面以几道最近模拟考非常火又颇有难度的题作为例题，秒杀之．【例10】（2019•济南二模）已知函数()22x f x ax bx -=--+，若对任意的实数a b ，，总存在[]012x ∈-，，使得()0f x m≥成立，则实数m 的取值范围是 ．A ．14⎛⎤-∞ ⎥⎝⎦，B ．12⎛⎤-∞ ⎥⎝⎦，C ．23⎛⎤-∞ ⎥⎝⎦，D ．(]1-∞，【例11】（2019•武汉调研）已知函数()3f x x ax b =++的定义域为[1,2]-，记()f x 的最大值为M ，则M 的最小值为（ ） A ．4B ．3C ．2D ．3【例12】（2019•青浦二模）设函数()()2f x ax b a R x=-+∈,若对任意的正实数a ，总存在[]01,2x ∈，使得()0f x m ≥，求实数m 的最小值为 ．308【例13】（2016•天津理）设函数3()(1)f x x ax b =---，x R ∈，其中a ，b R ∈． （1）求()f x 的单调区间；（2）若()f x 存在极值点0x ，且10()()f x f x =，其中10x x ≠，求证：1023x x +=； （3）设0a >，函数()|()|g x f x =，求证：()g x 在区间[0，2]上的最大值不小于14．秒杀秘籍：第五讲 常见方法之三点控制（多点控制）在这类求最大值的最小值问题中，多点控制也是一个非常好用的处理手段，这里给到大家一些总结，怎么取点控制：①对于二次函数一般用三点控制，这三点分别是区间的两个端点和区间中点；①对于平口打勾函数一般用三点控制，这三点分别是区间的两个端点和极值点，对于一般的打勾函数，这三点分别是区间的两个端点和打勾函数两区间端点连线平行且与打勾函数相切的直线与打勾函数的切点； ①对于一般的三次函数，一般需要四点控制，这四点分别是区间的两个端点和分别靠近两端点的两个四等分点．注意：对于缺少常数项的二次函数和缺项的三次函数，选取点的原则可能会发生改变，视情况而定． （注：此公式参考微信公众号《万卷归宗文献》） 【例14】已知函数()2f x x ax b=++，[]01x ∈，，若()f x 的最大值是M ，则M 的最小值是 ．【例15】已知函数 ()328f x x ax bx =--，是否存在任意实数a b 、，使得()2f x ≤对任意的[]11x ∈-，恒成立，若存在，求出a b 、，若不存在，说明理由．【例16】已知函数()f x x ax b -，a b R ∈、，若对任意的[]004x ∈，，使得()0f x M ≥，求实数M 的取值范围是 ．309达标训练1．（2018•永康模拟）记()()ln 0f x x ax b a =++>在区间[],2t t +（t 为正数）上的最大值为(),t M a b ，若(){},ln 2t b M a b a R ≥+=，则实数t 的最大值是（ ） A ．2B ．1C ．34D ．232．已知34a ≥-，0b ≥，函数()3f x x ax b =++，11x -≤≤，设()f x 的最大值为M ，对任意的,a b R ∈恒有M k ≥，则实数k 的最大值为（ ） A ．4B ．2C ．12D ．143．（2016•沙坪坝月考）已知函数()()3223(33)1,f x x x a x +b a b R =-+-≥∈，当[]0,2x ∈时，记()f x 的最大值为M ，有M k ≥，则实数k 的最大值为（ ） A ．1B ．2C ．3D ．44．（2018•诸暨二模）已知函数2()||f x x ax b =++在区间[0，]c 内的最大值为(M a ，b R ∈，0c >位常数） 且存在实数a ，b ，使得M 取最小值 2 ，则a b c ++= ． 5．（2017•温州二模）若存在]1,1[0-∈x 使得不等式0001|421|2x x x a +-⋅+…成立，则实数a 的取值范围是 ．6．（2016•浙江二模）设1()42(,)x x f x a b a b R +=+⋅+∈，若对于[0x ∀∈，1]，1|()|2f x …都成立， 则b = ． 7．函数()2f x x ax =-在[]01，上的最大值的最小值为 ，此时a = ．8．函数()2f x x ax =-在[]36，上的最大值的最小值为 ，此时a = ． 9．函数()2f x x ax =-在[]13，上的最大值的最小值为 ，此时a = ．10．若函数()224f x x ax b π⎛⎫+++ ⎪⎝⎭在302x π⎡⎤∈⎢⎥⎣⎦，上最大值为M ，则的M 最小值为 ． 11．已知函数()1f x x ax b x =+--，当122x ⎡⎤∈⎢⎥⎣⎦，时，设()f x 的最大值为M ，则的M 最小值为 ．12．若存在实数a b 、使得()221x ax b m x ++≤+对于任意的[]1,1x ∈-恒成立，则的m 最小值为 ．13．设函数()32f x x ax bx c a b c R=+++∈，、、，若对任意的实数a b c 、、，总存在[]00,4x ∈，使得不等式()0f x M≥成立，则实数M 的取值范围是 ．14．（2018•温州期末）已知函数2()(4)3f x x a x a =+-+-． （1） 若()f x 在区间[0，1]上不单调， 求a 的取值范围；（2） 若对于任意的(0,4)a ∈，存在0[0x ∈，2]，使得0|()|f x t …，求t 的取值范围 ．31015．（2009•湖北）在R 上定义运算：1()()4(3p q p c q b bc b ⊗=---+、c R ∈是常数），已知21()2f x x c =-，2()2f x x b =-，12()()()f x f x f x =⊗．（1）如果函数()f x 在1x =处有极值43-，试确定b 、c 的值；（2）求曲线()y f x =上斜率为c 的切线与该曲线的公共点；（3）记()|()|(11)g x f x x ='-剟的最大值为M ，若M k …对任意的b 、c 恒成立，试求k 的取值范围．（参考公式：323234()(2))x bx b x b x b -+=+-16．（2016•浙江二模）已知函数2()2(,)f x x ax b a b R =-+∈，记M 是|()|f x 在区间[0，1]上的最大值． （1）当0b =且2M =时，求a 的值； （2）若12M …，证明01a 剟．17．（2016•天津）设函数3()f x x ax b =--，x R ∈，其中a ，b R ∈． （1）求()f x 的单调区间；（2）若()f x 存在极值点0x ，且10()()f x f x =，其中10x x ≠，求证：1020x x +=； （3）设0a >，函数()|()|g x f x =，求证：()g x 在区间[1-，1]上的最大值不小于14．。

平口单峰函数一、定义平口单峰函数是指在一定区间内，函数值先增后减，在某处取得最大值，然后再逐渐减小到最小值的一个函数。

它的图像呈现出一个平缓的口形，并且只有一个峰顶。

二、特点1. 函数值先增后减，在某处取得最大值，然后再逐渐减小到最小值。

2. 只有一个峰顶，呈现出平缓的口形。

3. 通常用于模拟人体感知过程中的响应曲线。

三、数学表达式平口单峰函数可以用以下数学表达式表示：f(x) = (x-a)^2e^{-b(x-a)}\cos(c(x-a))其中a,b,c为常数，x为自变量。

该函数图像如下所示：四、Python实现下面给出Python实现平口单峰函数的代码：```pythonimport numpy as npimport matplotlib.pyplot as pltdef unimodal_function(x, a=0, b=1, c=1):return (x - a) ** 2 * np.exp(-b * (x - a)) * np.cos(c * (x - a))x = np.linspace(-5, 5, 1000)y = unimodal_function(x)plt.plot(x, y)plt.show()```五、参数调节通过调节参数a,b,c可以改变函数的形态。

下面给出一些例子：1. 增大参数b，使得函数在峰顶处更加陡峭。

```pythony = unimodal_function(x, b=5)```2. 增大参数c，使得函数在峰顶处更加平缓。

```pythony = unimodal_function(x, c=5)```3. 改变参数a，可以改变函数的位置。

构造“平口单峰”函数解决一些恼人的“切比雪夫最佳逼近直线”一、新增此方法的的简单推广（16天津卷）。

二：引理证明bug 修正。

下面这些问题相信长期混群的人都不陌生，提问频率颇高。

大多数时候的解答为绝对值不等式配凑以及“切比雪夫最佳逼近直线”。

然后，没有人对最佳逼近直线给过论证，只是一句话带过。

本文将给出一种极其简洁的做法及解释。

1.1()42,(,),x x f x a b a b R +=++∈，若对任意的[0,1]x ∈，1|()|2f x ≤都成立，则b=_____。

2.设函数4()||f x ax x=-，若对任意的正实数a,总存在0[1,4]x ∈，使得0()f x m ≥，则实数m 的取值范围是______。

3.设函数()|,,f x ax b a b R =-∈，若对任意实数a,b,总存在实数0[0,4]x ∈，使得0()f x m ≥成立，则实数m 的取值范围为_______。

4.已知函数2()||f x x ax b =++在区间[0,]x c ∈内的最大值为M ，(,,0)a b R c ∈>为常数，且存在实数,a b 使得M 的最小值为2，则a+b+c=_______。

5.已知2()(4)3f x x a x a =+-+-对任意[0,4]a ∈，均存在0[0,2]x ∈，使得0|()|f x t ≥成立，则t 的取值范围是______。

6.设函数2()||f x ax b x=--，若对于任意实数a,b ，总存在0[1,2]x ∈，使得0()f x m ≥成立，则实数m 的取值范围是_______。

7.设函数2()||f x x ax b =++，若对于任意实数a,b ，总存在0[0,4]x ∈，使得0()f x m ≥成立，则实数m 的取值范围是_______。

8.已知函数1()||f x x ax b x =+--，当1[,2]2x ∈时，设()f x 的最大值为(,)M a b ，则(,)M a b 的最小值为______。

平口单峰函数求最值平口单峰函数求最值在数学中，求最值是一个重要的概念，它可以帮助我们确定函数的最小值或最大值。

其中最常见的是寻找单峰函数的最值，这里我们将重点介绍如何求解单峰函数的最值。

一、什么是单峰函数单峰函数，又称为单谷函数，是指具有单一的极值的函数。

它有一个唯一的最大值或最小值，因此也可以称为单峰或单谷函数。

它的图像是一个峰或谷，而不是一个曲线，因此它又称为平口函数。

二、求解单峰函数的最值1. 首先，我们需要求出函数的一阶导数，如果一阶导数为0，则说明函数可能存在最值。

2. 然后，我们需要求出函数的二阶导数，如果二阶导数为正，则说明函数的最值为最大值，如果二阶导数为负，则说明函数的最值为最小值。

3. 最后，我们可以求出函数的最值，即求出函数在最大值或最小值处的函数值。

三、平口单峰函数求最值实例下面我们来看一个具体的例子，求解平口单峰函数的最值。

首先，我们来看一个平口单峰函数：f(x)=x³-3x²+2。

接着，我们可以求出它的一阶导数：f'(x)=3x²-6x。

求出一阶导数后，我们可以观察一下它的值，当x=-2或x=2时，f'(x)=0，这说明函数可能存在最值。

接着，我们可以求出函数的二阶导数：f"(x)=6x-6。

求出二阶导数后，我们可以看出f"(x)=-6，这说明函数的最小值为最值，即当x=-2时，函数值最小，f(-2)=2。

最后，我们可以求出函数的最小值：f(-2)=2。

四、总结以上就是关于如何求解平口单峰函数的最值的介绍。

总的来说，我们需要先求出函数的一阶导数和二阶导数，当一阶导数为0时，函数可能存在最值，当二阶导数为正时，函数的最值为最大值，当二阶导数为负时，函数的最值为最小值，最后我们可以求出函数的最值。

单峰映射python-概述说明以及解释1.引言1.1 概述单峰映射是一种在数学和计算机领域中常见的概念，它描述了一个函数在定义域上存在且仅存在一个极值点或者局部最值点的映射关系。

在实际应用中，单峰映射常常用于优化问题的求解，例如在遗传算法、模拟退火算法等优化算法中的应用较为广泛。

本文将重点介绍单峰映射在Python编程语言中的应用。

通过对单峰映射的概念和原理进行深入剖析，我们将探讨如何利用Python编程实现单峰映射，并通过实际案例加以说明。

最后，我们还将总结单峰映射的重要性，归纳Python中实现单峰映射的方法，以及展望单峰映射在未来的应用前景。

通过本文的阐述，读者将能够更好地理解和应用单峰映射这一重要概念。

1.2 文章结构文章结构部分主要介绍了整篇文章的框架和组成部分，包括引言、正文和结论三个部分。

在引言部分，我们会对单峰映射这一概念进行概述，介绍文章的结构和目的。

在正文部分，我们将深入探讨单峰映射的定义、在Python中的应用以及实际案例。

最后在结论部分，我们将总结单峰映射的重要性，总结Python中实现单峰映射的方法，并展望单峰映射在未来的应用前景。

整篇文章将以逻辑清晰、内容丰富的方式呈现给读者，让他们更好地了解和掌握单峰映射在Python中的应用。

1.3 目的：本文旨在介绍单峰映射在Python中的应用以及实际案例，旨在帮助读者更好地理解和应用单峰映射这一概念。

通过深入探讨单峰映射的概念和原理，读者可以了解其在数据处理、优化算法等领域中的重要性和实际应用场景。

同时，本文还将介绍Python中实现单峰映射的方法，帮助读者通过具体的实例更好地掌握相关知识和技能。

通过本文的阅读，读者可以深入了解和学习单峰映射这一概念，了解其在Python编程中的应用，从而为进一步学习和应用相关算法奠定基础。

希望本文能够帮助读者更好地理解单峰映射，激发读者对该领域的兴趣，为其在相关领域的研究和实践提供帮助和指导。

构造“平口单峰”函数解决一些恼人的“切比雪夫最佳逼近直线”一、新增此方法的的简单推广（16天津卷）。

二：引理证明bug 修正。

下面这些问题相信长期混群的人都不陌生，提问频率颇高。

大多数时候的解答为绝对值不等式配凑以及“切比雪夫最佳逼近直线”。

然后，没有人对最佳逼近直线给过论证，只是一句话带过。

本文将给出一种极其简洁的做法及解释。

1.1()42,(,),x x f x a b a b R +=++∈，若对任意的[0,1]x ∈，1|()|2f x ≤都成立，则b=_____。

2.设函数4()||f x ax x=-，若对任意的正实数a,总存在0[1,4]x ∈，使得0()f x m ≥，则实数m 的取值范围是______。

3.设函数()|,,f x ax b a b R =-∈，若对任意实数a,b,总存在实数0[0,4]x ∈，使得0()f x m ≥成立，则实数m 的取值范围为_______。

4.已知函数2()||f x x ax b =++在区间[0,]x c ∈内的最大值为M ，(,,0)a b R c ∈>为常数，且存在实数,a b 使得M 的最小值为2，则a+b+c=_______。

5.已知2()(4)3f x x a x a =+-+-对任意[0,4]a ∈，均存在0[0,2]x ∈，使得0|()|f x t ≥成立，则t 的取值范围是______。

6.设函数2()||f x ax b x=--，若对于任意实数a,b ，总存在0[1,2]x ∈，使得0()f x m ≥成立，则实数m 的取值范围是_______。

7.设函数2()||f x x ax b =++，若对于任意实数a,b ，总存在0[0,4]x ∈，使得0()f x m ≥成立，则实数m 的取值范围是_______。

8.已知函数1()||f x x ax b x =+--，当1[,2]2x ∈时，设()f x 的最大值为(,)M a b ，则(,)M a b 的最小值为______。

单峰拟合函数选取（原创实用版）目录1.介绍单峰拟合函数选取的背景和重要性2.阐述单峰拟合函数的定义和特点3.描述单峰拟合函数选取的方法和过程4.分析单峰拟合函数选取的优缺点5.总结单峰拟合函数选取的意义和应用前景正文1.介绍单峰拟合函数选取的背景和重要性在数据分析和建模领域，单峰拟合函数选取是一个关键环节。

在实际应用中，我们常常需要根据一组数据来拟合一个函数，以便更好地理解数据背后的规律。

在这个过程中，选择一个合适的拟合函数对于获得准确的拟合结果至关重要。

单峰拟合函数作为一种特殊的拟合函数，具有良好的性质和广泛的应用场景，因此对其选取方法的研究具有重要的理论和实践意义。

2.阐述单峰拟合函数的定义和特点单峰拟合函数是指能够最好地拟合一组数据的函数，其特点是在数据集上只有一个局部极小值。

根据这一特点，单峰拟合函数可以分为凸函数和非凸函数两类。

其中，凸函数具有唯一的全局极小值，因此容易求解；非凸函数则可能有多个局部极小值，求解起来较为复杂。

在实际应用中，根据数据的特性和问题的需求，可以选择不同类型的单峰拟合函数进行拟合。

3.描述单峰拟合函数选取的方法和过程选取单峰拟合函数的方法可以分为两类：基于梯度的方法和基于牛顿法的方法。

（1）基于梯度的方法：这类方法主要利用函数的梯度信息来进行搜索。

常见的算法有梯度下降法、拟牛顿法、梯度提升树等。

这些方法在求解过程中，通过不断地更新参数，使得目标函数值逐渐收敛到最小值。

（2）基于牛顿法的方法：这类方法利用牛顿迭代公式来进行搜索。

具体来说，通过二阶导数信息来构造搜索方向，从而加速收敛过程。

基于牛顿法的方法有牛顿法、拟牛顿法等。

4.分析单峰拟合函数选取的优缺点单峰拟合函数选取方法具有一定的优点，例如求解速度快、收敛性能好等。

然而，它也存在一些缺点，如容易受到初始值影响、对于非凸函数求解困难等。

因此，在实际应用中，需要根据具体情况选择合适的方法。

5.总结单峰拟合函数选取的意义和应用前景单峰拟合函数选取在数据分析和建模领域具有重要意义，它可以帮助我们更好地理解数据背后的规律，从而为实际问题提供有效的解决方案。

平口单峰之我见--北京张立祥武汉四调一出，平口单峰再现江湖，到底什么是平口单峰呢，好多老师觉得不太理解，遇到有人问题也只是甩下“平口单峰”，好像就已经解决了一样，听得问题人一脸蒙蔽，觉得自己见识太浅，不敢再问。

由于这种情况的增多，小编决定把自己理解的平口单峰分享给大家（特别感谢杨岸杰老师给出的不断指导）首先，这个名词是由重庆南开野猪（吴剑）老师提出，后被群内推广。

首先看一个题例1、已知函数b ax x x f --=2)(,当]2,2[-∈x 时设()f x 的最大值为(,)M a b ，则(,)M a b 的最小值为_______这里的(,)M a b 我们可以理解为函数]2,2[,2-∈=x x y 和直线b ax y +=的铅锤距离的最大值，由于b a ,没有限制，所以我们可以规定任意直线.比如我们先假设直线有斜率，此时M 应该为图中所标长度1d 还是2d 呢？应该是2d ，因为这两个函数是同一个x ，所以要求横坐标相等的时候纵坐标的差最大，此时M=5;那么我们再来看下图，此时M 等于多少呢？应该是图中的1d 长度，具体等于多少需要计算.有人可能有疑问，在2d 的右侧有没有可能有一条直线比1d 还长呢？其实是有可能的，这时候的计算方法应该是用直线的解析式减去抛物线的解析式再求解，但是M 会大于2.我们再来几个图来感受一下也就是说，在斜率存在情况下，M 的值总会比2大，读者可自行再多画几个体会一下.此时我们再来体会一下当斜率为0的情况下，M 的变化过程。

此时我们发现M 有最小值可以为2，由于b a ,没有限定，所以我们可以令2,0==b a ，此时(,)M a b 的最小值为2.也就是对于两端点相等的单峰曲线，铅锤距离最大值的最小值应该在两端点连线和最低点平行的直线的中间产生.（我并没有给出证明，读者可自行百度野猪平口单峰进行参考）到此，我们就可以试着理解平口单峰了，若)(x f 为],[n m 上的连续单峰函数，且0),()(x n f m f =为极值点，则当b k ,变化时，b kx x f x g --=)()(的最大值的最小值为2)()(0x f n f -（也就是21（最大-最小））。

专题16函数与导数常见经典压轴小题全归类【命题规律】1、导数的计算和几何意义是高考命题的热点，多以选择题、填空题形式考查，难度较小．2、应用导数研究函数的单调性、极值、最值多在选择题、填空题靠后的位置考查，难度中等偏上，属综合性问题．【核心考点目录】核心考点一：函数零点问题之分段分析法模型核心考点二：函数嵌套问题核心考点三：函数整数解问题核心考点四：唯一零点求值问题核心考点五：等高线问题核心考点六：分段函数零点问题核心考点七：函数对称问题核心考点八：零点嵌套问题核心考点九：函数零点问题之三变量问题核心考点十：倍值函数核心考点十一：函数不动点问题核心考点十二：函数的旋转问题核心考点十三：构造函数解不等式核心考点十四：导数中的距离问题核心考点十五：导数的同构思想核心考点十六：不等式恒成立之分离参数、分离函数、放缩法核心考点十七：三次函数问题核心考点十八：切线问题核心考点十九：任意存在性问题核心考点二十：双参数最值问题核心考点二十一：切线斜率与割线斜率核心考点二十二：最大值的最小值问题（平口单峰函数、铅锤距离）核心考点二十三：两边夹问题和零点相同问题核心考点二十四：函数的伸缩变换问题【真题回归】1．（2022·全国·统考高考真题）当1x =时，函数()ln bf x a x x=+取得最大值2-，则(2)f '=（ ） A ．1-B ．12-C ．12D ．12．（2022·全国·统考高考真题）函数()()cos 1sin 1f x x x x =+++在区间[]0,2π的最小值、最大值分别为（ ）A ．ππ22-，B ．3ππ22-， C ．ππ222-+，D ．3ππ222-+， 3．（多选题）（2022·全国·统考高考真题）已知函数3()1f x x x =-+，则（ ） A ．()f x 有两个极值点B ．()f x 有三个零点C ．点(0,1)是曲线()y f x =的对称中心D ．直线2y x =是曲线()y f x =的切线4．（2022·天津·统考高考真题）设a ∈R ，对任意实数x ，记(){}2min 2,35f x x x ax a =--+-．若()f x 至少有3个零点，则实数a 的取值范围为______.5．（2022·全国·统考高考真题）已知1x x =和2x x =分别是函数2()2e x f x a x =-（0a >且1a ≠）的极小值点和极大值点．若12x x <，则a 的取值范围是____________．6．（2022·全国·统考高考真题）若曲线()e x y x a =+有两条过坐标原点的切线，则a 的取值范围是________________．7．（2022·浙江·统考高考真题）已知函数()22,1,11,1,x x f x x x x ⎧-+≤⎪=⎨+->⎪⎩则12f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭________；若当[,]x a b ∈时，1()3f x ≤≤，则b a -的最大值是_________．8．（2022·全国·统考高考真题）曲线ln ||y x =过坐标原点的两条切线的方程为____________，____________． 9．（2022·北京·统考高考真题）设函数()()21,,2,.ax x a f x x x a -+<⎧⎪=⎨-≥⎪⎩若()f x 存在最小值，则a 的一个取值为________；a 的最大值为___________．【方法技巧与总结】1、求分段函数的函数值，要先确定要求值的自变量属于哪一段区间，然后代入该段的解析式求值，当出现()()f f a 的形式时，应从内到外依次求值；当给出函数值求自变量的值时，先假设所求的值在分段函数定义区间的各段上，然后求出相应自变量的值，切记要代入检验，看所求的自变量的值是否满足相应段自变量的取值范围．2、含有抽象函数的分段函数，在处理时首先要明确目标，即让自变量向有具体解析式的部分靠拢，其次要理解抽象函数的含义和作用（或者对函数图象的影响）．3、含分段函数的不等式在处理上通常有两种方法：一种是利用代数手段，通过对x 进行分类讨论将不等式转变为具体的不等式求解；另一种是通过作出分段函数的图象，数形结合，利用图象的特点解不等式．4、分段函数零点的求解与判断方法：（1）直接法：直接根据题设条件构造关于参数的不等式，再通过解不等式确定参数范围； （2）分离参数法：先将参数分离，转化成球函数值域的问题加以解决；（3）数形结合法：先将解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．5、动态二次函数中静态的值：解决这类问题主要考虑二次函数的有关性质及式子变形，注意二次函数的系数、图象的开口、对称轴是否存在不变的性质，二次函数的图象是否过定点，从而简化解题．6、动态二次函数零点个数和分布问题：通常转化为相应二次函数的图象与x 轴交点的个数问题，结合二次函数的图象，通过对称轴，根的判别式，相应区间端点函数值等来考虑．7、求二次函数最值问题，应结合二次函数的图象求解，有三种常见类型： （1）对称轴变动，区间固定； （2）对称轴固定，区间变动； （3）对称轴变动，区间也变动．这时要讨论对称轴何时在区间之内，何时在区间之外．讨论的目的是确定对称轴和区间的关系，明确函数的单调情况，从而确定函数的最值．8、由于三次函数的导函数为我们最熟悉的二次函数，所以基本的研究思路是：借助导函数的图象来研究原函数的图象．如借助导函数的正负研究原函数的单调性；借助导函数的（变号）零点研究原函数的极值点（最值点）；综合借助导函数的图象画出原函数的图象并研究原函数的零点…具体来说，对于三次函数()()32 0f x ax bx cx d a =+++＞，其导函数为()()232 0f x ax bx c a '=++＞，根的判别式()243b ac ∆=-．增区间：(), x -∞，0∆≤恒成立，三次函数()f x 在R 上为增函数，没有极值点，有且只有一个零点；（2）当0∆≥时，()0f x '=有两根1x ，2x ，不妨设12x x ＜，则1223b x x a+=-，可得三次函数()f x 在()1, x -∞，()2, x +∞上为增函数，在()12, x x 上为减函数，则1x ，2x 分别为三次函数()32f x ax bx cx d=+++的两个不相等的极值点，那么：① 若()()120f x f x ⋅＞，则()f x 有且只有1个零点； ② 若()()120f x f x ⋅＜，则()f x 有3个零点； ③ 若()()120f x f x ⋅=，则()f x 有2个零点．特别地，若三次函数()()32 0f x ax bx cx d a =+++＞存在极值点0x ，且()00f x =，则()f x 地解析式为()()()20f x a x x x m =--．同理，对于三次函数()()32 0f x ax bx cx d a =+++＜，其性质也可类比得到．9、由于三次函数()()32 0f x ax bx cx d a =+++≠的导函数()232f x ax bx c '=++为二次函数，其图象变化规律具有对称性，所以三次函数图象也应当具有对称性，其图象对称中心应当为点, 33bb faa ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，此结论可以由对称性的定义加以证明．事实上，该图象对称中心的横坐标正是三次函数导函数的极值点．10、对于三次函数图象的切线问题，和一般函数的研究方法相同．导数的几何意义就是求图象在该店处切线的斜率，利用导数研究函数的切线问题，要区分“在”与“过”的不同，如果是过某一点，一定要设切点坐标，然后根据具体的条件得到方程，然后解出参数即可．11、恒成立（或存在性）问题常常运用分离参数法，转化为求具体函数的最值问题．12、如果无法分离参数，可以考虑对参数或自变量进行分类讨论，利用函数性质求解，常见的是利用函数单调性求解函数的最大、最小值．13、当不能用分离参数法或借助于分类讨论解决问题时，还可以考虑利用函数图象来求解，即利用数形结合思想解决恒成立（或存在性）问题，此时应先构造函数，作出符合已知条件的图形，再考虑在给定区间上函数图象之间的关系，得出答案或列出条件，求出参数的范围．14、两类零点问题的不同处理方法利用零点存在性定理的条件为函数图象在区间[a ，b ]上是连续不断的曲线，且()()0f a f b ⋅<．．①直接法：判断-一个零点时，若函数为单调函数，则只需取值证明()()0f a f b ⋅<．②分类讨论法：判断几个零点时，需要先结合单调性，确定分类讨论的标准，再利用零点存在性定理，在每个单调区间内取值证明()()0f a f b ⋅<．15、利用导数研究方程根（函数零点）的技巧（1）研究方程根的情况，可以通过导数研究函数的单调性、最大值、最小值、变化趋势等． （2）根据题目要求，画出函数图象的走势规律，标明函数极（最）值的位置．（3）利用数形结合的思想去分析问题，可以使问题的求解有一个清晰、直观的整体展现． 16、已知函数零点个数求参数的常用方法（1）分离参数法：首先分离出参数，然后利用求导的方法求出构造的新函数的最值，根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围．（2）分类讨论法：结合单调性，先确定参数分类的标准，在每个小范围内研究零点的个数是否符合题意，将满足题意的参数的各小范围并在一起，即为所求参数范围．【核心考点】核心考点一：函数零点问题之分段分析法模型 【典型例题】例1．（2023·浙江奉化·高二期末）若函数322ln ()x ex mx xf x x -+-=至少存在一个零点，则m 的取值范围为（ ） A ．21,e e ⎛⎤-∞+ ⎥⎝⎦B ．21,e e ⎡⎫++∞⎪⎢⎣⎭C ．1,e e ⎛⎤-∞+ ⎥⎝⎦D ．1,e e ⎡⎫++∞⎪⎢⎣⎭例2．（2023·天津·耀华中学高二期中）设函数()322ln f x x ex mx x =-+-，记()()f xg x x=，若函数()g x 至少存在一个零点，则实数m 的取值范围是 A ．21,e e ⎛⎤-∞+ ⎥⎝⎦B ．210,e e ⎛⎤+ ⎥⎝⎦C ．21e ,e ⎛⎫++∞ ⎪⎝⎭D ．2211e ,e e e ⎛⎤--+ ⎥⎝⎦例3．（2023·湖南·长沙一中高三月考（文））设函数()22x xf x x x a e=--+（其中e 为自然对数的底数），若函数()f x 至少存在一个零点，则实数a 的取值范围是（ ） A ．1(0,1]e+B ．1(0,]e e +C ．1[,)e e ++∞D ．1(,1]e-∞+核心考点二：函数嵌套问题 【典型例题】例4．（2023·全国·高三专题练习）已知函数2()(1)x f x x x e =--，设关于x 的方程25()()()f x mf x m R e-=∈有n 个不同的实数解，则n 的所有可能的值为A ．3B ．1或3C ．4或6D ．3或4或6例5．（2023·全国·高三专题练习（文））已知函数()||12x f x e =-，()()11,021ln ,0x x g x x x x ⎧+≤⎪=⎨⎪->⎩若关于x 的方程()()0g f x m -=有四个不同的解，则实数m 的取值集合为（ ） A ．ln 20,2⎛⎫ ⎪⎝⎭B ．ln 2,12⎛⎫⎪⎝⎭C ．ln 22⎧⎫⎨⎬⎩⎭D ．()0,1例6．（2023·河南·高三月考（文））已知函数()ln x f x x=，若关于x 的方程()()210f x af x a ++-=⎡⎤⎣⎦有且仅有三个不同的实数解，则实数a 的取值范围是( ) A ．()2e,1e --B ．()1e,0-C ．(),1e -∞-D ．()1e,2e -核心考点三：函数整数解问题 【典型例题】例7．（2023·福建宁德·高三）当1x >时，()41ln ln 3k x x x x --<-+恒成立，则整数k 的最大值为（ ） A ．2-B ．1-C ．0D ．1例8．（2023·江苏·苏州大学附属中学高三月考）已知a Z ∈，关于x 的一元二次不等式260x x a -+≤的解集中有且仅有3个整数，则所有符合条件的a 的值之和是（ ） A ．13B ．21C ．26D ．30例9．（2023·江苏宿迁·高一月考）用符号[x ]表示不超过x 的最大整数（称为x 的整数部分），如[﹣1.2]=﹣2，[0.2]=0，[1]=1，设函数f （x ）=（1﹣ln x ）（ln x ﹣ax ）有三个不同的零点x 1，x 2，x 3，若[x 1]+[x 2]+[x 3]=6，则实数a 的取值范围是（ ） A ．10,e ⎛⎫⎪⎝⎭B ．ln 31,3e ⎛⎫⎪⎝⎭ C ．ln 21,2e ⎡⎫⎪⎢⎣⎭ D ．ln 2ln 3,23⎡⎫⎪⎢⎣⎭ 核心考点四：唯一零点求值问题 【典型例题】例10．（2023·安徽蚌埠·模拟预测（理））已知函数()()()2ln 1ln f x x x a x =-+--有唯一零点，则a =（ ）A ．0B ．12-C ．1D ．2例11．（2023·辽宁沈阳·模拟预测）已知函数()(),g x h x 分别是定义在R 上的偶函数和奇函数，且()()x g x h x e x +=+，若函数()()12216x f x g x λλ-=+--有唯一零点，则正实数λ的值为（ ）A ．12B ．13C ．2D ．3例12．（2023·新疆·莎车县第一中学高三期中）已知函数()g x ，()h x 分别是定义在R 上的偶函数和奇函数，且()()sin xg x h e x x x ++=-，若函数()()20202320202x f g x x λλ-=---有唯一零点，则实数λ的值为 A ．1-或12B ．1或12-C ．1-或2D ．2-或1核心考点五：等高线问题 【典型例题】例13．（2023·陕西·千阳县中学模拟预测（理））已知函数2()log 1f x x =-，若方程()f x a =(0)a >的4个不同实根从小到大依次为1x ，2x ，3x ，4x ，有以下三个结论：①142x x +=且232x x +=；②当1a =时，12111x x +=且34111x x +=；③21340x x x x +=．其中正确的结论个数为（ ） A ．0 B ．1 C ．2 D ．3例14．（2023·江苏省天一中学高三月考）已知函数2()(2)x f x x x e =-，若方程()f x a =有3个不同的实根()123123x x x x x x <<，，，则22ax -的取值范围为（ ） A ．10e⎡⎫-⎪⎢⎣⎭，B．1e⎡-⎢⎣⎭C．()D．(例15．（2023·浙江·高一单元测试）已知函数(){}2max ,32f x x x =-，其中{},max ,,p p q p q q p q ≥⎧=⎨<⎩，若方程()()302f x ax a =+>有四个不同的实根1x 、2x 、3x 、()41234x x x x x <<<，则1423x x x x ++的取值范围是（ ）A ．93,102⎫⎛-- ⎪⎝⎭B ．193,102⎫⎛-- ⎪⎝⎭C ．39,210⎫⎛- ⎪⎝⎭D ．319,210⎫⎛- ⎪⎝⎭核心考点六：分段函数零点问题 【典型例题】例16．（2023·山东青岛·高三期末）已知函数2|ln(1),1()(2),1x x f x x x ⎧+-=⎨+≤-⎩，若方程()0f x m -=有4个不相同的解，则实数m 的取值范围为（ ） A ．(0,1]B ．[0,1)C ．(0,1)D ．[0,1]例17．（2023·全国·高三专题练习）已知函数2log ,1()11,14x x f x x x >⎧⎪=⎨+≤⎪⎩，()()g x f x kx =-，若函数()g x 有两个零点，则k 的取值范围是（ ） A ．10,4⎛⎤⎥⎝⎦B ．10,ln 2e ⎛⎫ ⎪⎝⎭C ．10,e ⎡⎫⎪⎢⎣⎭D ．11,42eln ⎡⎫⎪⎢⎣⎭例18．（2023·江苏·高三专题练习）已知函数22,0()log ,0x x f x x x ⎧≤=⎨>⎩，函数()()g x f x x m =++，若()g x 有两个零点，则m 的取值范围是（ ）． A ．[1,)-+∞B ．(,1]-∞-C ．[0,)+∞D ．[1,0)-核心考点七：函数对称问题 【典型例题】例19．（2023·安徽省滁州中学高三月考（文））已知函数()22ln ,03,02x x x x f x x x x ->⎧⎪=⎨--≤⎪⎩的图象上有且仅有四个不同的点关于直线1y =的对称点在10kx y +-=的图象上,则实数k 的取值范围是A ．1,12⎛⎫⎪⎝⎭B ．13,24⎛⎫ ⎪⎝⎭C ．1,13⎛⎫ ⎪⎝⎭D ．1,22⎛⎫ ⎪⎝⎭例20．（2023·全国·高一课时练习）若直角坐标平面内的两点P ，Q 满足条件：①P ，Q 都在函数()f x 的图象上；②P ，Q 关于原点对称，则称点对[],P Q 是函数()f x 的一个“友好点对”（注：点对[],P Q 与[],Q P 看作同一个“友好点对”）．已知函数()22log ,04,0x x f x x x x >⎧=⎨--≤⎩，则此函数的“友好点对”有（ ）A ．0个B ．1个C ．2个D ．3个例21．（2023·福建·厦门一中高一竞赛）若函数y ＝f (x )图象上存在不同的两点A ，B 关于y 轴对称，则称点对[A ，B ]是函数y ＝f (x )的一对“黄金点对”（注：点对[A ，B ]与[B ，A ]可看作同一对“黄金点对”）已知函数2229,0()4,041232,4x x f x x x x x x x +<⎧⎪=-+≤≤⎨⎪-+>⎩，则此函数的“黄金点对”有（ ）A ．0对B ．1对C ．2对D ．3对核心考点八：零点嵌套问题 【典型例题】例22．（2023·湖北武汉·高三月考）已知函数2()()(1)()1x x f x xe a xe a =+-+-有三个不同的零点123,,x x x .其中123x x x <<，则3122123(1)(1)(1)x x x x e x e x e ---的值为（ ）A ．1B ．2(1)a -C ．1-D ．1a -例23．（2023·全国·模拟预测（理））已知函数2()e e x x x ax f x a ⎛⎫=+- ⎪⎝⎭有三个不同的零点123,,x x x （其中123x x x <<），则3122312111e e ex x x x x x ⎛⎫⎛⎫⎛⎫--- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭的值为 A ．1B ．1-C ．aD ．a -例24．（2023·浙江省杭州第二中学高三开学考试）已知函数()()()2ln ln f x ax x x x x =+--，有三个不同的零点，（其中123x x x <<），则2312123ln ln ln 111x x x x x x ⎛⎫⎛⎫⎛⎫---⎪ ⎪⎪⎝⎭⎝⎭⎝⎭的值为 A ．1a - B ．1a - C ．-1 D ．1核心考点九：函数零点问题之三变量问题 【典型例题】例25．（2023·全国·高三）若存在两个正实数x 、y ，使得等式3(24)(ln ln )0x a y ex y x +--=成立，其中e 为自然对数的底数，则实数a 的取值范围是（ ）．A ．()0-∞，B ．3(0)[)2e-∞⋃+∞，， C ．3(0]2e，D ．3[)2e+∞， 例26．（2023·山东枣庄·高二期末）对于任意的实数[1,e]x ∈，总存在三个不同的实数y ，使得ln 0ye xy x ay y--=成立，其中e 为自然对数的底数，则实数a 的取值范围是A ．2(,)4e -∞-B ．2(,0)4e -C ．2[,)4e -+∞D ．2(,)4e -+∞例27．（2023·四川省新津中学高三月考（理））若存在两个正实数,x y ，使得等式330yx x e ay -=成立，其中e 为自然对数的底数，则实数a 的取值范围为A ．2[,)8e +∞B ．3(0,]27eC ．3[,)27e +∞D ．2(0,]8e核心考点十：倍值函数 【典型例题】例28．（河南省郑州市第一中学2022-2023学年高三上学期期中考试数学（理）试题）对于函数()y f x =，若存在区间[],a b ，当[],x a b ∈时的值域为[](),0ka kb k >，则称()y f x =为k 倍值函数.若()2xf x e x =+是k倍值函数，则实数k 的取值范围是（ ） A ．()1,e ++∞B ．()2,e ++∞C ．1,e e ⎛⎫++∞ ⎪⎝⎭D ．,e e 2⎛⎫++∞ ⎪⎝⎭例29．（2023·四川·内江市教育科学研究所高二期末（文））对于函数()y f x =，若存在区间,a b ，当[],x a b ∈时，()f x 的值域为[],ka kb ，则称()y f x =为k 倍值函数.若()xf x e =是k 倍值函数，则k 的取值范围为（ ）A ．10,e ⎛⎫⎪⎝⎭B ．()1,eC ．(),e +∞D ．1,e ⎛⎫+∞ ⎪⎝⎭例30．（2023·吉林·长春十一高高二期中（理））对于函数()y f x =，若存在区间[],a b ，当[],x a b ∈时，()f x 的值域为[],ka kb ，则称()y f x =为k 倍值函数．若()ln f x x x =+是k 倍值函数，则k 的取值范围为（ ） A ．10,e ⎛⎫ ⎪⎝⎭B ．1,e ⎛⎫+∞ ⎪⎝⎭C ．11,1e ⎛⎫+ ⎪⎝⎭D ．11,e ⎛⎫++∞ ⎪⎝⎭核心考点十一：函数不动点问题 【典型例题】例31．（2023·广东海珠·高三期末）设函数()f x a R e ∈，为自然对数的底数），若曲线y x x =上存在点00()x y ，使得00()f y y =，则a 的取值范围是（ ） A ．1e[1]e-, B ．1e[e 1]e-+， C ．[1e 1]+， D ．[1,e]例32．（2023·山西省榆社中学高三月考（理））若存在一个实数t ，使得()F t t =成立，则称t 为函数()F x 的一个不动点.设函数()1(xg x e x a =+-(a R ∈，e 为自然对数的底数)，定义在R 上的连续函数()f x 满足()()2f x f x x -+=，且当0x ≤时，()f x x '<.若存在01|()(1)2x x f x f x x ⎧⎫∈+-+⎨⎬⎩⎭，且0x 为函数()g x 的一个不动点，则实数a 的取值范围为（ ）A ．⎛⎫-∞ ⎪ ⎪⎝⎭ B ．⎡⎫+∞⎪⎢⎪⎣⎭ C ．⎛⎤⎥ ⎝⎦ D ．⎛⎫+∞⎪ ⎪⎝⎭例33．（2023·四川自贡·高二期末（文））设函数()()1ln 2=+-∈f x x x a a R ，若存在[]1,b e ∈(e 为自然对数的底数)，使得()()f f b b =，则实数a 的取值范围是（ ） A ．1,122⎡⎤--⎢⎥⎣⎦eB ．e 1,ln 212⎡⎤--⎢⎥⎣⎦C ．1,ln 212⎡⎤--⎢⎥⎣⎦D ．1,02⎡⎤-⎢⎥⎣⎦核心考点十二：函数的旋转问题 【典型例题】例34．（2023·上海市建平中学高三期末）双曲线2213x y -=绕坐标原点O 旋转适当角度可以成为函数f （x ）的图象，关于此函数f （x ）有如下四个命题，其中真命题的个数为（ ） ①f （x ）是奇函数；②f （x ）的图象过点32⎫⎪⎪⎝⎭或32⎫-⎪⎪⎝⎭； ③f （x ）的值域是33,,22⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭；④函数y ＝f （x ）－x 有两个零点． A ．4个B ．3个C ．2个D ．1个例35．（2023·山东青岛·高三开学考试）将函数2([3,3])y x =∈-的图象绕点(3,0)-逆时针旋转(0)ααθ≤≤，得到曲线C ，对于每一个旋转角α，曲线C 都是一个函数的图象，则θ最大时的正切值为（ ）A ．32B ．23C ．1D 例36．（2023·浙江·高三期末）将函数π2sin 0,22x y x ⎛⎫⎡⎤=∈ ⎪⎢⎥⎣⎦⎝⎭的图像绕着原点逆时针旋转角α得到曲线T ，当(]0,αθ∈时都能使T 成为某个函数的图像，则θ的最大值是（ ）A ．π6B ．π4C ．3π4D ．2π3核心考点十三：构造函数解不等式 【典型例题】例37．（2023·江西赣州·高三期中（文））已知函数()()f x x R ∈满足(1)1f =，且()f x 的导数1()2f x '>，则不等式||1(||)22x f x <+的解集为（ ） A ．(,1)-∞-B ．(1,)+∞C ．(1,1)-D ．(,1][1,)-∞-+∞例38．（2023·全国·高二课时练习）设定义在R 上的函数()f x 的导函数为()'f x ，若()()'2f x f x +<，()02021f =，则不等式()22019x x e f x e >+（其中e 为自然对数的底数）的解集为（ ） A ．()0+∞，B ．()2019+∞，C ．()0-∞，D ．()()02019-∞+∞，，例39．（2023·全国·高二课时练习）已知()f x 的定义域为0,，()'f x 为()f x 的导函数，且满足()()f x xf x '<-，则不等式()()()2111f x x f x +>--的解集是（ ）A ．0,1B ．2,C ．1,2D ．1,核心考点十四：导数中的距离问题 【典型例题】例40．（2023春•荔湾区期末）设函数22()()(22)f x x a lnx a =-+-，其中0x >，a R ∈，存在0x 使得04()5f x 成立，则实数a 的值是( ) A ．15B ．25C ．12D ．1例41．（2023•龙岩模拟）若对任意的正实数t ，函数33()()()3f x x t x lnt ax =-+--在R 上都是增函数，则实数a 的取值范围是( )A ．1(,]2-∞B ．(-∞C ．(-∞D ．(-∞，2]例42．（2023•淮北一模）若存在实数x 使得关于x 的不等式2221()22x e a x ax a -+-+成立，则实数a 的取值范围是( ) A ．1{}2B ．1{}4C ．1[2，)+∞D ．1[4，)+∞核心考点十五：导数的同构思想 【典型例题】例43．（2023·全国·高三专题练习）已知关于x 的不等式ln ln(1)0x e mx x m ---+≥在(0,)+∞恒成立，则m 的取值范围是（ ） A ．(]1,1-B ．(]1,1e --C ．(]1,1e -D ．(]1,e例44．（2023·安徽·合肥一中高三月考（理））设实数0m ＞，若对任意的()1,x ∈+∞，不等式2ln 20mxxe m-≥恒成立，则实数m 的取值范围是（ ） A ．1,2e ⎡⎫+∞⎪⎢⎣⎭B ．1,2⎡⎫+∞⎪⎢⎣⎭C ．[)1,+∞D ．[),e +∞例45．（2023·宁夏·石嘴山市第一中学高二月考（理））若对任意()0,x ∈+∞，不等式ln 0ax ae x ->恒成立，则实数a 的取值范围为（ ）A ．1,e e ⎛⎫- ⎪⎝⎭B ．1,e⎛⎫+∞ ⎪⎝⎭C ．1e e ⎛⎫ ⎪⎝⎭,D ．(),e +∞核心考点十六：不等式恒成立之分离参数、分离函数、放缩法 【典型例题】例46．（2023·浙江·高三月考）已知函数2()1x f x xe =-，不等式()ln f x mx x ≥+对任意(0,)x ∈+∞恒成立，则实数m 的取值范围是（ ） A ．(,2]-∞B ．[0,2]C ．(2,e 1⎤-∞-⎦D ．20,1e ⎡⎤-⎣⎦例47．（2023·四川省资中县第二中学高二月考（理））关于x 的不等式()32ln 113x x a x xe x+++-≥对任意0x >恒成立，则a 的取值范围是（ ）． A ．(],1-∞-B ．(){},1e -∞⋃C ．[],1e --D ．(],0-∞例48．（2023·全国·高三专题练习）已知,a b ∈R ，若关于x 的不等式2ln 0x a x a b -+-≥恒成立，则ab 的最大值为_______．核心考点十七：三次函数问题 【典型例题】例49．（2023·全国·高三课时练习）设函数()y f x ''=是()y f x '=的导数，经过探究发现，任意一个三次函数()()320ax bx d a f x cx =+++≠的图象都有对称中心()()00,x f x ，其中0x 满足()00f x ''=，已知函数()3272392f x x x x =-+-，则12320212022202220222022f f f f ⎛⎫⎛⎫⎛⎫⎛⎫+++⋅⋅⋅+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭（ ） A ．2021 B ．20212C ．2022D ．40212例50．（2023·安徽·东至县第二中学高三月考（理））人们在研究学习过程中，发现：三次整式函数()f x 都有对称中心，其对称中心为00(,())x f x （其中0''()0f x =）.已知函数32()345f x x x x =-++.若()4,()10f m f n ==，则m n +=（ ） A ．1B ．32C ．2D ．3例51．（2023·全国·高三月考（文））已知m ，n ，p ∈R ，若三次函数()32f x x mx nx p =+++有三个零点a ，b ，c ，且满足()()3112f f -=<，()()022f f =>，则111a b c ++的取值范围是（ ）A ．1,13⎛⎫ ⎪⎝⎭B ．11,43⎛⎫ ⎪⎝⎭C ．11,42⎛⎫⎪⎝⎭D ．11,32⎛⎫ ⎪⎝⎭核心考点十八：切线问题 【典型例题】例52．（2023·云南红河·高三月考（理））下列关于三次函数32()(0)()f x ax bx cx d a x R =+++≠∈叙述正确的是（ ）①函数()f x 的图象一定是中心对称图形； ②函数()f x 可能只有一个极值点； ③当03bx a≠-时，()f x 在0x x =处的切线与函数()y f x =的图象有且仅有两个交点； ④当03bx a≠-时，则过点()()00,x f x 的切线可能有一条或者三条． A ．①③B ．②③C ．①④D ．②④例53．（2023·江西·南昌二中高三月考（文））若函数2()1f x x =+的图象与曲线C:()21(0)x g x a e a =⋅+>存在公共切线，则实数a 的取值范围为 A ．220,e ⎛⎤ ⎥⎝⎦B ．240,e ⎛⎤ ⎥⎝⎦C ．21,e ⎡⎫+∞⎪⎢⎣⎭D ．23,e ⎡⎫+∞⎪⎢⎣⎭例54．（2023·全国·高二单元测试）若过点(),a b 可以作曲线e x y =的两条切线，则( ) A ．e b a <B ．e b a >C ．0e b a <<D ．0e a b <<核心考点十九：任意存在性问题 【典型例题】例55．（2023·河南·郑州外国语中学高三月考（理））若不等式()()()221212log 1log 3,,13x xa x x ++-≥-∈-∞恒成立，则实数a 的范围是（ ） A ．[0,)+∞B ．[1,)+∞C ．(,0]-∞D ．(,1]-∞.例56．（2023·全国·高三专题练习）已知函数2()=++f x x px q 对,∀∈p q R ，总有0[1,5]∃∈x ，使()0f x m≥成立，则m 的范围是（ ） A ．5,2⎛⎤-∞ ⎥⎝⎦B ．(,2]-∞C ．(,3]-∞D ．(,4]-∞例57．（2023·全国·高二课时练习）已知()()1ln f x x x =+，若k ∈Z ，且()()2k x f x -<对任意2x >恒成立，则k 的最大值为（ ） A ．3B ．4C ．5D ．6核心考点二十：双参数最值问题 【典型例题】例58．（2023·浙江·宁波市北仑中学高三开学考试）已知,a b ∈R ，且0ab ≠，对任意0x >均有()()(ln )0x a b x a x b ----≥，则（ ） A ．0,0a b <<B ．0,0a b <>C ．0,0a b ><D ．0,0a b >>例59．（2023·山西运城·高三期中（理））已知在函数()()0,0f x ax b a b =+>>，()()ln 2g x x =+，若对2x ∀>-，()()f x g x ≥恒成立，则实数ba的取值范围为（ ）A ．[)0,+∞B ．[)1,+∞C ．[)2,+∞D ．[),e +∞例60．（2023·黑龙江·鹤岗一中高三月考（理））当(1,)x ∈+∞时，不等式ln(1)230(x ax b a --+，b R ∈，0)a ≠恒成立，则ba 的最大值为（ ）A ．1eB ．2C ．43D ．2e核心考点二十一：切线斜率与割线斜率 【典型例题】例61．（2023·广东·佛山一中高三月考）已知函数2()ln (1)1h x a x a x =+-+(0)a < ，在函数()h x 图象上任取两点,A B ，若直线AB 的斜率的绝对值都不小于5，则实数a 的取值范围是（ ）A ．(,0)-∞B ．⎛-∞ ⎝⎦C ．,⎛-∞ ⎝⎦D ．⎫⎪⎪⎝⎭例62．（2023·山西大同·高一期中）已知函数(),()f x g x 是定义在R 上的函数，且()f x 是奇函数，()g x 是偶函数，()()f x g x +=2x ax +，记2()()()g x h x xf x x =+，若对于任意的1212x x <<<，都有()()12120h x h x x x -<-，则实数a 的取值范围为（ ） A ．1,02⎡⎫-⎪⎢⎣⎭B ．(0,)+∞C ．(,1]-∞-D ．(0,2]例63．（2023·全国·高一课时练习）已知函数(),142,12x a x f x a x x ⎧≥⎪=⎨⎛⎫-+< ⎪⎪⎝⎭⎩，若对任意的1x ，2x ，且12x x ≠，都有()()12120f x f x x x ->-成立，则实数a 的取值范围是（ ）A ．()1,+∞B ．[)1,8C ．()4,8D ．[)4,8核心考点二十二：最大值的最小值问题（平口单峰函数、铅锤距离） 【典型例题】例64．设二次函数2()(2)32f x a x ax =-++在R 上有最大值，最大值为m （a ），当m （a ）取最小值时，(a =) A ．0B ．1C ．12D例65．（2023春•绍兴期末）已知函数2()||||f x x a x b =+++，[0x ∈，1]，设()f x 的最大值为M ，若M 的最小值为1时，则a 的值可以是( ) AB ．0 CD ．1例66．（2023•济南模拟）已知函数2()||2x f x ax b x -=--+，若对任意的实数a ，b ，总存在0[1x ∈-，2]，使得0()f x m 成立，则实数m 的取值范围是( ) A ．1(,]4-∞B ．(-∞，1]2C ．(-∞，2]3D ．(-∞，1]核心考点二十三：两边夹问题和零点相同问题 【典型例题】例67．（2023春•湖州期末）若存在正实数x ，y 使得不等式22414lnx x lny ln y -++-成立，则(xy += ) ABCD 例68．（2023•上饶二模）已知实数x ，y 满足2(436)326x y ln x y e x y +-+--+-，则x y +的值为( ) A ．2B ．1C ．0D ．1-例69．（2023•崇明区期末）若不等式(||)sin()06x a b x ππ--+对[1x ∈-，1]恒成立，则a b +的值等于() A ．23B ．56C ．1D ．2核心考点二十四：函数的伸缩变换问题 【典型例题】例70．（2023·天津一中高三月考）定义域为R 的函数()f x 满足()()22f x f x +=，当[]0,2x 时，()[)[)232,0,11,1,22x x x x f x x -⎧-∈⎪⎪=⎨⎛⎫-∈⎪ ⎪⎪⎝⎭⎩，若当[)4,2x ∈--时，不等式()2142m f x m ≥-+恒成立，则实数m 的取值范围是（ ） A ．[]2,3 B ．[]1,3 C ．[]1,4D ．[]2,4例71．（2023·浙江·杭州高级中学高三期中）定义域为R 的函数()f x 满足(2)3()f x f x +=，当[0,2]x ∈时，2()2f x x x =-，若[4,2]x ∈--时，13()()18≥-f x t t恒成立，则实数t 的取值范围是( ) A ．(](],10,3-∞-B．((,0,3⎤-∞⎦C ．[)[)1,03,-+∞D ．))3,⎡⎡+∞⎣⎣例72．（2023届山西省榆林市高三二模理科数学试卷）定义域为R 的函数()f x 满足()()22f x f x +=，当[)0,2x ∈时，()[)[)2213,0,1{ln ,1,2x x x f x x x x -+∈=∈，若当[)4,2x ∈--时，函数()22f x t t ≥+恒成立，则实数t 的取值范围为（ ） A ．30t -≤≤B ．31t -≤≤C ．20t -≤≤D ．01t ≤≤【新题速递】一、单选题1．（2023·广西南宁·南宁二中校考一模）已知函数()2,01,011x x f x x x x ⎧≤⎪=-≤<⎨≥，若函数()()()22231g x m f x mf x =-+，存在5个零点，则m =（ ） A ．1B ．12C ．1或12D ．1-2．（2023春·陕西西安·高三统考期末）已知函数()e ,03,0x x f x x x ⎧≥=⎨-<⎩， 若函数()()()g x f x f x =--，则函数()g x 的零点个数为（ ）A ．1B ．3C ．4D ．53．（2023·江西景德镇·统考模拟预测）已知函数()11,041,0x xf x x x ⎧+<⎪⎪=⎨⎪->⎪⎩，若()()12f x f x =，则12x x -的最小值为（ ） A ．4B ．92C ．143D ．54．（2023春·内蒙古赤峰·高三统考阶段练习）已知实数0a >，0b >，1a b +=，则下列说法中，正确的是（ ）． A ．114a b+≤B ．存在a ，b ，使得223a b +≥C ．22log log 1a b ⋅≤D ．存在a ，b ，使得直线10ax by 与圆224x y +=相切5．（2023·全国·高三专题练习）已知()0,2A ，()(),00B t t <，动点C 在曲线T ：()2401y x x =≤≤上，若△ABC 面积的最小值为1，则t 不可能为（ ） A ．4-B ．3-C ．2-D ．1-6．（2023·浙江温州·统考模拟预测）已知P 为直线=1y x --上一动点，过点P 作抛物线2:2C x y =的两条切线，切点记为A ，B ，则原点到直线AB 距离的最大值为（ ） A ．1BCD ．27．（2023春·江西赣州·高三赣州市赣县第三中学校考期中）已知0a >，0b >，直线2e y x b -=+与曲线ln y x a =-相切，则11a b+的最小值是（ ） A ．16B ．12C ．8D ．48．（2023春·江苏苏州·高三苏州中学校考阶段练习）若关于x 的不等式(41ln )ln 3k x x x x --<-+对于任意(1,)x ∈+∞恒成立，则整数k 的最大值为（ ） A ．-2 B ．-1 C ．0 D ．1二、多选题9．（2023·江苏苏州·苏州中学校考模拟预测）已知函数()e xf x x =-，()lng x x x =-，则下列说法正确的是（ ）A ．()e xg 在()0,∞+上是增函数B ．1x ∀>，不等式()()2ln f ax f x ≥恒成立，则正实数a 的最小值为2eC ．若()f x t =有两个零点12,x x ，则120x x +>D ．若()()()122f x g x t t ==>，且210x x >>，则21ln t x x -的最大值为1e10．（2023春·重庆·高三统考阶段练习）已知函数32()e 3xf x ax =-有三个不同的极值点1x ，2x ，3x ，且123x x x <<，则下列结论正确的是（ ）A ．2e 8a >B ．11x <-C ．2x 为函数()f x 的极大值点D ．()23e 3f x <11．（2023春·福建宁德·高三校考阶段练习）已知函数()3f x x ax b =++，其中a ，b 为实数，则下列条件能使函数()f x 仅有一个零点的是（ ） A ．3a =-，3b =-B ．3a =-，2b =C ．0a =，3b =-D ．1a =，2b =12．（2023春·山东潍坊·高三统考期中）定义在R 上的函数()f x 的导函数为()f x '，对于任意实数x ，都有2()e ()x f x f x -=，且满足22()()21e x f x f x x -'+=+-，则（ ）A ．函数()e ()x F x f x =为偶函数B ．(0)0f =C ．不等式e ()e e x xxf x +<的解集为(1,)+∞ D ．若方程2()()0f x x a x--=有两个根12,x x ，则122x x a +> 13．（2023·浙江温州·统考模拟预测）若函数()y f x =的图象上存在两个不同的点P ，Q ，使得()f x 在这两点处的切线重合，则称函数()y f x =为“切线重合函数”，下列函数中是“切线重合函数”的是（ ） A ．sin cos y x x =+ B ．(sin c s )o y x = C ．sin y x x =+D ．2sin y x x =+14．（2023春·江苏南京·高三统考阶段练习）已知双曲线C ：224x y -=，曲线E ：2y ax x b =++，记两条曲线过点()1,0的切线分别为1l ，2l ，且斜率均为正数，则（ ） A ．若=0a ，1b =，则C 与E 有一个交点 B ．若=1a ，=0b ，则C 与E 有一个交点C ．若0a b ，则1l 与E 夹角的正切值为7-D ．若==1a b ，则1l 与2l 三、填空题15．（2023·河南郑州·高三阶段练习）正实数a ，b 满足1e 4a a +=+，()ln 3b b +=，则b a -的值为____________． 16．（2023·全国·高三校联考阶段练习）已知函数()234202312342023x x x x f x x =+-+-++，()234202312342023x x x x g x x =-+-+--，设()()()53F x f x g x =+⋅-，且函数()F x 的零点均在区间[](a b a b <，，a ，)b Z ∈内，则b a -的最小值为__________．17．（2023春·广东广州·高三统考阶段练习）方程e 0x ax a -+=有唯一的实数解，实数a 的取值范围为__________．18．（2023春·山东·高三山东省实验中学校考阶段练习）已知函数()()23e ,? 0e ,? 0x x xf x x a x ⎧->=⎨-≤⎩，若()()12f x f x =，且12x x -的最大值为4，则实数a 的值为_______．19．（2023·全国·高三专题练习）若存在0a >，0b >，满足(2e )ln (2e )ln a t b a b t b a a +-=-，其中e 为自然对数的底数，则实数t 的取值范围是___________．20．（2023·四川资阳·统考模拟预测）若2224ln x ax a x ->，则a 的取值范围是______．。

压轴题03函数与导数常见经典压轴小题1、导数的计算和几何意义是高考命题的热点，多以选择题、填空题形式考查，难度较小．2、应用导数研究函数的单调性、极值、最值多在选择题、填空题靠后的位置考查，难度中等偏上，属综合性问题．考向一：函数、零点嵌套问题考向二：函数整数解问题考向三：等高线问题考向四：零点问题考向五：构造函数解不等式考向六：导数中的距离问题考向七：导数的同构思想考向八：最大值的最小值问题（平口单峰函数、铅锤距离）1、分段函数零点的求解与判断方法：（1）直接法：直接根据题设条件构造关于参数的不等式，再通过解不等式确定参数范围；（2）分离参数法：先将参数分离，转化成球函数值域的问题加以解决；（3）数形结合法：先将解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．2、由于三次函数的导函数为我们最熟悉的二次函数，所以基本的研究思路是：借助导函数的图象来研究原函数的图象．如借助导函数的正负研究原函数的单调性；借助导函数的（变号）零点研究原函数的极值点（最值点）；综合借助导函数的图象画出原函数的图象并研究原函数的零点，具体来说，对于三次函数()()32 0f x ax bx cx d a =+++＞，其导函数为()()232 0f x ax bx c a '=++＞，根的判别式()243b ac ∆=-．a ＞()232f x ax bx c'=++判别式∆＞0∆=0∆＜图象()32f x ax bx cx d=+++单调性增区间：()1, x -∞，()2, x +∞；减区间：()12, x x 增区间：(), -∞+∞增区间：(), -∞+∞图象（1）当0∆≤时，()0f x '≥恒成立，三次函数()f x 在R 上为增函数，没有极值点，有且只有一个零点；（2）当0∆≥时，()0f x '=有两根1x ，2x ，不妨设12x x ＜，则1223bx x a+=-，可得三次函数()f x 在()1, x -∞，()2, x +∞上为增函数，在()12, x x 上为减函数，则1x ，2x 分别为三次函数()32f x ax bx cx d =+++的两个不相等的极值点，那么：①若()()120f x f x ⋅＞，则()f x 有且只有1个零点；②若()()120f x f x ⋅＜，则()f x 有3个零点；③若()()120f x f x ⋅=，则()f x 有2个零点．特别地，若三次函数()()32 0f x ax bx cx d a =+++＞存在极值点0x ，且()00f x =，则()f x 地解析式为()()()20f x a x x x m =--．同理，对于三次函数()()32 0f x ax bx cx d a =+++＜，其性质也可类比得到．3、由于三次函数()()32 0f x ax bx cx d a =+++≠的导函数()232f x ax bx c '=++为二次函数，其图象变化规律具有对称性，所以三次函数图象也应当具有对称性，其图象对称中心应当为点, 33bb faa ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，此结论可以由对称性的定义加以证明．事实上，该图象对称中心的横坐标正是三次函数导函数的极值点．4、恒成立（或存在性）问题常常运用分离参数法，转化为求具体函数的最值问题．5、如果无法分离参数，可以考虑对参数或自变量进行分类讨论，利用函数性质求解，常见的是利用函数单调性求解函数的最大、最小值．6、当不能用分离参数法或借助于分类讨论解决问题时，还可以考虑利用函数图象来求解，即利用数形结合思想解决恒成立（或存在性）问题，此时应先构造函数，作出符合已知条件的图形，再考虑在给定区间上函数图象之间的关系，得出答案或列出条件，求出参数的范围．7、两类零点问题的不同处理方法利用零点存在性定理的条件为函数图象在区间[a ，b ]上是连续不断的曲线，且()()0f a f b ⋅<．．①直接法：判断-一个零点时，若函数为单调函数，则只需取值证明()()0f a f b ⋅<．②分类讨论法：判断几个零点时，需要先结合单调性，确定分类讨论的标准，再利用零点存在性定理，在每个单调区间内取值证明()()0f a f b ⋅<．8、利用导数研究方程根（函数零点）的技巧（1）研究方程根的情况，可以通过导数研究函数的单调性、最大值、最小值、变化趋势等．（2）根据题目要求，画出函数图象的走势规律，标明函数极（最）值的位置．（3）利用数形结合的思想去分析问题，可以使问题的求解有一个清晰、直观的整体展现．9、已知函数零点个数求参数的常用方法（1）分离参数法：首先分离出参数，然后利用求导的方法求出构造的新函数的最值，根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围．（2）分类讨论法：结合单调性，先确定参数分类的标准，在每个小范围内研究零点的个数是否符合题意，将满足题意的参数的各小范围并在一起，即为所求参数范围．1．（2023·江西宜春·统考模拟预测）已知函数()()()ln 1,ln (0)1m xf x xg x x m x m=+-=+>+，且()()120f x g x ==，则()2111em x x -+的最大值为（）A ．1B ．eC ．2eD ．1e【答案】A【解析】()()()()()ln 10,ln 10,1ln 1,11m mf x x x m x x x x =+-=+-==++++()ln0,e ,x xg x x m x m=+==由题意知，()()21121ln 1e ,x x x x m ++==即()()2221121ln 1e e ln e ,x x xx x x m ++===因为0m >，所以21e 1,11xx >+>，设()ln ,1p x x x x =>，则()1ln 0p x x '=+>，()()211e ,xp x p m +==所以211e x x +=，所以()22121111e e e ex m m m x x x m---+==，1(),0e m m t m m -=>，则11(),e m m t m --'=当01m <<时，()0;t m '>当1m >时，()0;t m '<所以()t m 在()0,1时单调递增，在()1,+∞时单调递减，所以max ()(1)1,t m t ==故选：A.2．（2023·湖南岳阳·统考二模）若函数()22ln 2e 2ln x xf x a x ax -=-+有两个不同的零点，则实数a 的取值范围是（）A ．(),e -∞-B ．(],e -∞-C ．()e,0-D ．()【答案】A【解析】函数()f x 的定义域为(0,)+∞，()()222ln 22ln 2e 2ln e 2ln x x x x f x a x ax a x x --=-+=+-，设2()2ln (0)h x x x x =->，则22(1)(1)()2x x h x x x x+-'=-=，令()01h x x '>⇒>，令()001h x x '<⇒<<，所以函数()h x 在(0,1)上单调递减，在(1,)+∞上单调递增，且(1)1h =，所以min ()(1)1h x h ==，所以()1h x ≥，函数()f x 有两个不同的零点等价于方程()0f x =有两个不同的解，则()222ln 2ln 22e e 2ln 02ln x x x x a x x a x x--+-=⇒-=-，等价于函数y a =-与22ln 2e 2ln x xy x x-=-图象有两个不同的交点.令22ln x x t -=，()1e ,tg t tt =>，则函数y a =-与()1e ,tg t tt =>图象有一个交点，则()()22e 1e e 0tt t t t g t t t '--==>，所以函数()g t 在(1,)+∞上单调递增，所以()()1e g t g >=，且t 趋向于正无穷时，()e tg t t=趋向于正无穷，所以e a ->，解得e a <-.故选：A.3．（2023·江西吉安·统考一模）已知,R,0,0x y x y ∈>>，且2x y xy +=，则8e y x-的可能取值为（）（参考数据： 1.1e 3≈， 1.2e 3.321≈）A ．54B ．32C ．e 1-D ．e【答案】D【解析】由2x y xy +=，可得844x y =-且1y >，所以84e e 4y yx y-=+-，令()()4e 4,1,yg y y y =+-∈+∞，可得()24e y g y y='-，令()24e yh y y =-，可得()38e 0yh y y '=+>，()h y 为单调递增函数，即()g y '单调递增，又()()1.1 1.222441.1e 0, 1.2e 01.1 1.2g g =--'<'=>，所以存在()0 1.1,1.2y ∈，使得()00204e 0yg y y =-='，所以()()0min 002000444e 44, 1.1,1.2yg g y y y y y ==+-=-∈，设()0200444f y y y =+-，则()0320084f y y y =--'，因为()0 1.1,1.2y ∈，所以()00f y '<，所以()0f y 在()1.1,1.2上单调递减，所以()()0191.229f y f >=>，又因为()22e 2e g =->，()g y 在()0,y ∞+上递增，所以D 正确.故选：D.4．（2023·河南开封·开封高中校考一模）若存在[)1,x ∞∈+，使得关于x 的不等式11e x ax +⎛⎫+≥ ⎪⎝⎭成立，则实数a 的最小值为（）A ．2B ．1ln2C ．ln21-D ．11ln2-【答案】D 【解析】由11e x ax +⎛⎫+≥ ⎪⎝⎭两边取对数可得 1()ln 11x a x ⎛⎫++≥ ⎪⎝⎭①，令11,t x +=则11x t =-，因为[)1,x ∞∈+，所以(1,2]t ∈，则①可转化得1ln 11a t t ⎛⎫+≥⎪-⎝⎭，因为ln 0t >，11ln 1a t t ∴≥--因为存在[)1,x ∞∈+，使得关于x 的不等式11e x ax +⎛⎫+≥ ⎪⎝⎭成立，所以存在(1,2]t ∈，11ln 1a t t ≥--成立，故求11ln 1t t --的最小值即可，令11(),(1,2]ln 1g x x x x =-∈-2211()(ln )(1)g x x x x '∴=-+⋅-2222(ln )(1)(1)(ln )x x x x x x ⋅--=-2222222(1)1(ln )(ln )2(1)(ln )(1)(ln )x x x x x x x x x x ----+==--，令()h x 21(ln )2,(1,2]x x x x=--+∈212ln 11()2ln 1x x x h x x x xx-+'∴=⋅-+=，令1()2ln ,(1,2]x x x x xϕ=-+∈，2222121()1x x x x x x ϕ-+-'∴=--=22(1)0x x --=<，所以()ϕx 在(1,2]上单调递减，所以()(1)0x ϕϕ<=，()0h x '∴<，所以()h x 在(1,2]上单调递减，所以()(1)0,()0,h x h g x '<=∴<()g x ∴在(1,2]上单调递减，1()(2)1ln 2g x g ∴≥=-，11ln 2a ∴≥-，所以实数a 的最小值为11ln 2-故选：D5．（2023·河北石家庄·统考一模）已知210x x a -=在()0,x ∈+∞上有两个不相等的实数根，则实数a 的取值范围是（）A ．10,2e ⎛⎤ ⎥⎝⎦B ．10,2e ⎛⎫⎪⎝⎭C ．12e 1,e ⎛⎤ ⎥⎝⎦D ．12e 1,e ⎛⎫ ⎪⎝⎭【答案】D【解析】由()0,x ∈+∞，则210x x a =>，故2ln ln xa x=，要使原方程在()0,x ∈+∞有两个不等实根，即2ln ()xf x x =与ln y a =有两个不同的交点，由432ln 12ln ()x x x x f x x x --'==，令()0f x '>，则120e x <<，()0f x '<，则12e x >，所以()f x 在12(0,e )上递增，12(e ,)+∞上递减，故12max 1()(e )2e f x f ==，又x 趋向于0时，()f x 趋向负无穷，x 趋向于正无穷时，()f x 趋向0，所以，要使()f x 与ln y a =有两个不同的交点，则10ln 2ea <<，所以12e 1e a <<.故选：D6．（2023·吉林·统考三模）已知不等式22e ln ln x x λλ+≥在()0,x ∈+∞上恒成立，则实数λ的取值范围是（）A ．10,2e ⎛⎤ ⎥⎝⎦B ．10,4e ⎛⎤ ⎥⎝⎦C ．1,2e ∞⎡⎫+⎪⎢⎣⎭D ．1,4e ⎡⎫+∞⎪⎢⎣⎭【答案】C【解析】由22e ln ln x x λλ+≥得22e ln ln lnxxx λλλ≥-=，即22e lnxxxx λλ≥，令()e t f t t =，()0,t ∈+∞，则()()1e 0tf t t '=+>，所以()e tf t t =在()0,∞+上单调递增，而ln22e lnlne xxxxxx λλλλ≥=等价于()2ln x f x f λ⎛⎫≥ ⎪⎝⎭，∴2lnxx λ≥，即2e xx λ≥令()2e x g x x =，()0,x ∈+∞，则()212e xg x x-'=，所以()g x 在10,2x ⎛⎫∈ ⎪⎝⎭时()0g x '>，为增函数；在在1,2x ⎛⎫∈+∞ ⎪⎝⎭时()0g x '<，为减函数，所以()g x 最大值为1122e g ⎛⎫= ⎪⎝⎭，∴12e λ≥．故选：C7．（2023·黑龙江哈尔滨·哈尔滨三中校考二模）设()f x 是定义在R 上的可导函数，()f x 的导函数为()f x '，且()()32f x f x x '⋅>在R 上恒成立，则下列说法中正确的是（）A ．()()20232023f f <-B ．()()20232023f f >-C ．()()20232023f f <-D ．()()20232023f f >-【答案】D【解析】由题设32()()4f x f x x ⋅>'，构造24()()g x f x x =-，则3()2()()40g x f x f x x =-'>'，所以()g x 在R 上单调递增，则(2023)(2023)g g >-，即2424(2023)2023(2023)(2023)f f ->---，所以22(2023)(2023)f f >-，即()()20232023f f >-.故选：D8．（2023·四川广安·统考二模）若存在[]01,2x ∈-，使不等式()022002e 1ln e 2ex ax a x +-≥+-成立，则a 的取值范围是（）A ．21,e 2e ⎡⎤⎢⎥⎣⎦B ．221,e e ⎡⎤⎢⎥⎣⎦C ．421,e e ⎡⎤⎢⎥⎣⎦D ．41,e e ⎡⎤⎢⎥⎣⎦【答案】D【解析】()022002e 1ln e 2e x a x a x +-≥+-⇔()()222e 1ln e 12e x a a x ---≥-()()()000022222 e 1ln e 1ln e 2 e 1ln 2e e x x x x a a a a e ⇔---≥-⇔-≥-令ex at =，即()2e 1ln 220t t --+≥，因为0[1,2]x ∈-，所以21,e e a a t -⎡⎤∈⎢⎥⎣⎦，令()2()e 1ln 22f t t t =--+.则原问题等价于存在21,e e a a t -⎡⎤∈⎢⎥⎣⎦，使得()0f t ≥成立.()22e 12e 1()2t f t t t---'=-=令()0f t '<，即()2e 120,t --<解得2e 12t ->，令()0f t '>，即()2e 120,t -->解得2e 102t -<<，所以()f t 在2e 10,2⎛⎫- ⎪⎝⎭上单调递增，在2e 1,2⎛⎫-+∞⎪⎝⎭上单调递减.又因为()()2222(1)0,e e 1ln e 2e 2f f ==--+222e 22e 20=--+=而22e 11e 2-<<，∴当21e t ≤≤时，()0f t ≥.若存在21,e e a a t -⎡⎤∈⎢⎥⎣⎦，使得()0f t ≥成立.只需22e e a ≤且11e a -≥，解得4ea ≤且1e a ≥，所以41e ea ≤≤.故a 的取值范围为41,e e ⎡⎤⎢⎥⎣⎦.故选：D9．（2023·河南郑州·统考二模）函数()ln ,01,0x x x f x x x >⎧=⎨+≤⎩，若关于x 的方程()()()210f x m f x m -++=⎡⎤⎣⎦恰有5个不同的实数根，则实数m 的取值范围是（）A ．10em -<<B ．10em -<≤C ．10em -≤<D ．10em -≤≤【答案】A【解析】由()2[()]1()[()][()1]0f x m f x m f x m f x -++=--=，可得()f x m =或()1f x =，令ln y x x =且定义域为(0,)+∞，则ln 1y x ¢=+，当1(0,ex ∈时0'<y ，即y 递减；当1(,)ex ∈+∞时0'>y ，即y 递增；所以min 1e y =-，且1|0x y ==，在x 趋向正无穷y 趋向正无穷，综上，根据()f x 解析式可得图象如下图示：显然()1f x =对应两个根，要使原方程有5个根，则()f x m =有三个根，即(),f x y m =有3个交点，所以10em -<<.故选：A10．（2023·贵州·统考模拟预测）已知函数()f x 在R 上满足如下条件：（1）()()0f x f x -+=；（2）()20f -=；（3）当()0,x ∈+∞时，()()f x f x x'<.若()0f a >恒成立，则实数a 的值不可能是（）A ．3-B ．2C ．4-D ．1【答案】B 【解析】设()()f x g x x =，则()()()2xf x f x g x x'-'=，因为当()0,x ∈+∞时，()()f x f x x'<，所以当0x >时，有()()0xf x f x '-<恒成立，即此时()g x '<0，函数()g x 为减函数，因为()f x 在R 上满足()()0f x f x -+=，所以函数()f x 是奇函数，又()20f -=，所以()20f =，又()()()()()f x f x f x g x g x x x x---====--，故()g x 是偶函数，所以()()220g g =-=，且()g x 在(),0x ∈-∞上为增函数，当0a >时，()0f a >，即()()0f a ag a =>，等价为()0g a >，即()()2g a g >，得02a <<；当a<0时，()0f a >，即()()0f a ag a =>，等价为()0g a <，即()()2g a g <-，此时函数()g x 为增函数，得2a <-，综上不等式()0f a >的解集是()(),20,2-∞- ，结合选项可知，实数a 的值可能是3-，4-，1.故选：B11．（2023·广西·统考三模）已知2()cos f x x x =+，若3441e ,ln ,54a f b f c f -⎛⎫⎛⎫⎛⎫===- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则a ，b ，c 的大小关系为（）A ．b c a <<B ．c a b<<C ．c b a<<D ．a c b<<【答案】A【解析】因为2()cos ,R f x x x x =+∈，定义域关于原点对称，()22()()cos()cos f x x x x x f x -=-+-=+=，所以()f x 为R 上的偶函数，当0x ≥时,()2sin ,f x x x '=-，设()2sin g x x x =-，则()2cos g x x =-'，1cos 1x -≤≤ ，()0g x '∴>，所以()g x 即()f x '在[0,)+∞上单调递增，所以()(0)0f x f ''≥=,所以()f x 在[0,)+∞上单调递增，又因为()f x 为偶函数,所以()f x 在(,0]-∞上单调递减，又因为41ln0,054<-<,所以445ln ln ln 554b f f f ⎛⎫⎛⎫⎛⎫==-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,1144c f f ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭又因为31411ee e 4-->=>,因为141ln e 4=,41445e e, 2.4e 4⎛⎫⎛⎫=≈< ⎪ ⎪⎝⎭⎝⎭，所以145e 4>,所以145ln e ln 4>，即15ln 44>,所以3415eln 44->>,所以3441e 5ln 4f f f -⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎝⎭⎝⎭⎝⎭,即a c b >>.故选：A.12．（2023·天津南开·统考一模）已知函数()()216249,1,11,1,9x x x f x f x x ⎧-+≤⎪=⎨->⎪⎩则下列结论：①()1*9,Nn f n n -=∈②()()10,,x f x x∞∀∈+<恒成立③关于x 的方程()()R f x m m =∈有三个不同的实根，则119m <<④关于x 的方程()()1*9N n f x n -=∈的所有根之和为23n n +其中正确结论有（）A ．1个B ．2个C ．3个D ．4个【答案】B【解析】由题意知，()()()()1211111219999n n f n f n f n f n n --=-=-==--=⎡⎤⎣⎦ ，所以①正确；又由上式知，要使得()()10,,x f x x∞∀∈+<恒成立，只需满足01x <≤时，()1f x x <恒成立，即2116249x x x-+<，即321624910x x x -+-<恒成立，令()(]32162491,0,1g x x x x x =-+-∈，则()248489g x x x '=-+，令()0g x '=，解得14x =或34x =，当1(0,4x ∈时，()0g x '>，()g x 单调递增；当13(,)44x ∈时，()0g x '<，()g x 单调递减；当3(,)4x ∈+∞时，()0g x '>，()g x 单调递增，当14x =时，函数()g x 取得极大值，极大值11101444g f ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭，，所以②不正确；作出函数()f x 的图象，如图所示，由图象可知，要使得方程()()R f x m m =∈有三个不同的实根，则满足()()21f m f <<，即119m <<，所以③正确；由()1(1)9f x f x =-知，函数()f x 在(),1n n +上的函数图象可以由()1,n n -上的图象向右平移一个单位长度，再将所有点的横坐标不变，纵坐标变为原来的19倍得到，因为216249y x x =-+的对称轴为34x =，故()09f x =的两根之和为32，同理可得：()19f x =的两个之和为322+， ，()19nf x -=的两个之和为32(1)2n +-，故所有根之和为23333(2)[2(1)]2222n n n +++++-=+，所以④不正确.故选：B.13．（2023·山东济南·一模）函数()()()221xxx f x a a a =++-+（0a >且1a ≠）的零点个数为（）A ．1B ．2C ．3D ．4【答案】B【解析】由()0f x =可得22011x x a a a a +⎛⎫⎛⎫+-= ⎪ ⎪++⎝⎭⎝⎭，即11112011x xa a ⎛⎫⎛⎫-++-= ⎪ ⎪++⎝⎭⎝⎭，因为0a >且1a ≠，则1110,,1122a ⎛⎫⎛⎫∈ ⎪ ⎪+⎝⎭⎝⎭，令11t a =+，令()()()112x xg x t t =-++-，则()()010g g ==，()()()()()1ln 11ln 1xxg x t t t t '=--+++，令()()()()()1ln 11ln 1xxh x t t t t =--+++，则()()()()()221ln 11ln 10xxh x t t t t '=--+++>⎡⎤⎡⎤⎣⎦⎣⎦，所以，函数()g x '在R 上单调递增，因为()()()()20ln 1ln 1ln 1ln10g t t t'=-++=-<=，()()()()()11ln 11ln 1g t t t t '=--+++，令()()()()()1ln 11ln 1p t t t t t =--+++，其中01t <<，则()()()ln 1ln 10p t t t '=+-->，所以，函数()p t 在()0,1上单调递增，所以，()()()100g p t p >'==，由零点存在定理可知，存在()00,1x ∈，使得()00g x '=，且当0x x <时，()0g x '<，此时函数()g x 单调递减，当0x x >时，()0g x '>，此时函数()g x 单调递增，所以，()()()0010g x g g <==，所以，函数()g x 的零点个数为2，即函数()f x 的零点个数为2.故选：B.14．（2023·陕西榆林·统考二模）已知函数()()25e xf x x x =+-，若函数()()()()222g x f x a f x a =---⎡⎤⎣⎦恰有5个零点，则a 的取值范围是（）A ．()3e,0-B ．470,e ⎛⎫ ⎪⎝⎭C ．473e,e ⎛⎫- ⎪⎝⎭D ．()0,3e 【答案】B【解析】函数()g x 恰有5个零点等价于关于x 的方程()()()2220f x a f x a ⎡⎤---=⎣⎦有5个不同的实根．由()()()2220f x a f x a ⎡⎤---=⎣⎦，得()f x a =或()2f x =-．因为()()25e x f x x x =+-，所以()()234e x f x x x '=+-()()41e xx x =+-，由()0f x ¢>，得<4x -或1x >，由()0f x '<，得41x -<<，则()f x 在(),4-∞-和()1,+∞上单调递增，在()4,1-上单调递减．因为()474e f -=，()13e f =-，当x →+∞时，()f x →+∞，当x →-∞时，()0f x →，所以可画出()f x 的大致图象：由图可知()2f x =-有2个不同的实根，则()f x a =有3个不同的实根，故470,e a ⎛⎫∈ ⎪⎝⎭，故A ，C ，D 错误.故选：B.15．（2023·山东枣庄·统考二模）已知()f x =，a ∈R ，曲线cos 2y x =+上存在点()00,x y ，使得()()00f f y y =，则a 的范围是（）A ．()8,18ln 3+B ．[]8,18ln 3+C ．()9,27ln 3+D ．[]9,27ln 3+【答案】B【解析】因为[]cos 1,1x ∈-，所以[]cos 21,3y x =+∈，由题意cos 2y x =+上存在一点()00,x y 使得()()00f f y y =，即[]01,3y ∈，只需证明()00f y y =，显然()f x =假设()00f y y c =>，则()()()()000f f y f c c y f y ==>>不满足()()00f f y y =，同理()00f y c y =<不满足()()00f f y y =，所以()00f y y =，那么函数()[]1,3f x =即函数()f x x =在[]1,3x ∈有解，x =，可得[]2ln 9,1,3x x a x x +-=∈，从而[]2ln 9,1,3x x x a x +-=∈，令()[]2ln 9,1,3h x x x x x =+-∈，则()2119292x x h x x x x+-'=+-=，令()0h x '=，即21920x x +-=，解得12993,044x x -=>=（舍去），()0h x '>时03x <<<()0h x '<时x >所以()h x 在[]1,3单调递增，所以()()()13h h x h ≤≤，()1ln1918h =+-=，()3ln 3279ln 318h =+-=+，所以()h x 的取值范围为[]8,ln 318+，即a 的取值范围为[]8,ln 318+.故选：B.16．（2023·四川绵阳·盐亭中学校考模拟预测）已知()(0)ln kxx k xϕ=>，若不等式()11e kxxx ϕ+<+在()1+∞，上恒成立，则k 的取值范围为（）A ．1e⎛⎫+∞ ⎪⎝⎭，B ．()ln2+∞，C ．()0,eD ．()0,2e 【答案】A【解析】由题意知，(1,)x ∀∈+∞，不等式11e ln kx x kx x+<+恒成立，即()(1,),1eln e(1)ln kxkxx x x ∀∈+∞+>+成立.设()(1)ln (1)f x x x x =+>，则()e ()kxf f x >.因为11()ln ln 10x f x x x x x+'=+=++>，所以()f x 在()1+∞，上单调递增，于是e kx x >对任意的()1x ∈+∞，恒成立，即ln xk x >对任意的()1x ∈+∞，恒成立.令ln ()(1)x g x x x=>，即max ()k g x >.因为21ln ()xg x x-'=，所以当(1,e)x ∈时，()0g x '>;当()e x ∈+∞，时，()g x '<0，所以()g x 在(1,e)上单调递增，在()e ，+∞上单调递减，所以max 1()(e)eg x g ==，所以1ek >.故选：A .17．（2023·江西·校联考模拟预测）已知()ee 1ln x x a x+>有解，则实数a 的取值范围为（）A ．21,e ⎛⎫-+∞ ⎪⎝⎭B ．1,e⎛⎫-+∞ ⎪⎝⎭C ．()1,-+∞D ．1,e⎛⎫-∞ ⎪⎝⎭【答案】A【解析】不等式()e e 1ln x x a x+>可化为()e ln 1x a x x x ++>，()()e ln e 1x x a x x +>，令e x t x =，则ln 1at t +>且0t >，由已知不等式ln 1t at +>在()0,∞+上有解，所以1ln ta t ->在()0,∞+上有解.令()1ln t f t t -=，则()2ln 2t f t t ='-，当20e t <<时，()0f t '<，()f t 在()20,e 上单调递减；当2t e >时，()0f t '>，()f t 在()2e ,+∞单调递增，所以()min f t =()221e e f =-，所以21e a >-，所以a 的取值范围为21,e ⎛⎫-+∞ ⎪⎝⎭，故选：A.18．（2023·辽宁朝阳·校联考一模）设0k >，若不等式()ln e 0xk kx -≤在0x >时恒成立，则k 的最大值为（）A ．eB ．1C ．1e -D ．2e 【答案】A【解析】对于()ln e 0xk kx -≤，即()e ln x kx k≤，因为()ln y kx =是e xy k =的反函数，所以()ln y kx =与e xy k =关于y x =对称，原问题等价于e x x k≥对一切0x >恒成立，即e xk x≤；令()e x f x x =，则()()'21e x x f x x -=，当01x <<时，()()'0,f x f x <单调递减，当1x >时，()()'0,f x f x >单调递增，()()min 1e f x f ==，e k ∴≤；故选：A.19．（2023·四川南充·统考二模）已知函数()()2ln ln 1212x x h x t t x x ⎛⎫=--+- ⎪⎝⎭有三个不同的零点123,,x x x ，且123x x x <<．则实数11ln 1x x ⎛-⎝）A ．1t -B ．1t -C ．－1D ．1【答案】D 【解析】令ln x y x =，则21ln xy x-'=，当(0,e)x ∈时0'>y ，y 是增函数，当(e,)x ∈+∞时0'<y ，y 是减函数；又x 趋向于0时y 趋向负无穷，x 趋向于正无穷时y 趋向0，且e 1|ex y ==，令ln xm x=，则2()()(12)12h x g m m t m t ==--+-，要使()h x 有3个不同零点，则()g m 必有2个零点12,m m ，若11(0,e m ∈，则21em =或2(,0]m ∞∈-，所以2(12)120m t m t --+-=有两个不同的根12,m m ，则2Δ(12)4(12)0t t =--->，所以32t <-或12t >，且1212m m t +=-，1212m m t =-，①若32t <-，12124m m t +=->，与12,m m 的范围相矛盾，故不成立；②若12t >，则方程的两个根12,m m 一正一负，即11(0,)em ∈，2(,0)m ∞∈-；又123x x x <<，则12301e x x x <<<<<，且121ln x m x =，32123ln ln x x m x x ==，故11ln 1x x ⎛⎫- ⎪⎝⎭(()()221111m m m =-=--12121()1m m m m =-++=.故选：D20．（2023·陕西咸阳·武功县普集高级中学统考二模）已知实数0a >，e 2.718=…，对任意()1,x ∈-+∞，不等式()e e 2ln xa ax a ⎡⎤++⎣⎦≥恒成立，则实数a 的取值范围是（）A ．10,e ⎛⎤⎥⎝⎦B ．1,1e⎡⎫⎪⎢⎣⎭C ．20,e⎛⎫⎪⎝⎭D ．2,1e⎛⎫ ⎪⎝⎭【答案】A【解析】因为()e e 2ln xa ax a ⎡⎤++⎣⎦≥，所以()()1e2ln 2ln 2ln ln(1)x a ax a a a ax a a a a a x -⎡⎤++=++=+++⎣≥⎦，即11e 2ln ln(1)x a x a-⋅++≥+，即1ln 11ln e e 2ln ln(1)e 2ln ln(1)x x a a a x a x ---⋅+++⇔+≥++≥，所以1ln e 1ln ln(1)1x a x x a x --+≥--+++，令()e ,(1,)x f x x x =+∈-+∞，易知()f x 在()1,x ∈-+∞上单调递增，又因为ln(1)[ln(1)]e ln(1)1ln(1)x f x x x x ++=++=+++，所以(1ln )[ln(1)]f x a f x --≥+，所以1ln ln(1),(1,)x a x x --≥+∈-+∞，所以ln 1ln(1),(1,)a x x x ≤--+∈-+∞，令()1ln(1),(1,)g x x x x =--+∈-+∞，则1()111x g x x x '=-=++，所以当(1,0)x ∈-时，()0g x '<，()g x 单调递减；当,()0x ∈+∞时，()0g x '>，()g x 单调递增；所以min ()(0)1g x g ==-，所以ln 1a ≤-，解得10ea <≤.故选：A21．（2023·陕西榆林·统考二模）已知函数()()25e xf x x x =+-，若函数()()()()0g x f f x a a =->，则()g x 的零点个数不可能是（）A ．1B ．3C ．5D ．7【答案】D【解析】令()0g x =，即()()f f x a =，因为()()25e xf x x x =+-，所以()2()34e x f x x x '=+-，由()0f x ¢>，得<4x -或1x >，由()0f x '<，得41x -<<，则()f x 在(),4-∞-和()1,+∞上单调递增，在()4,1-上单调递减，因为()474e f -=，()13e f =-，当+x →∞时，()+f x →∞，当x →-∞时，()0f x →，令()0f x =，解得1212x -=或1212x -=，所以可画出()f x 的大致图像，设()t f x =，则()f t a =，第一种情况：当470e a <<时，()f t a =有三个不同的零点1t ，2t ，3t ，不妨设123t t t <<，则14t <-，2142t -<<-，312t ->，①讨论()1f x t =根的情况：当13e t <-时，()1f x t =无实数根，当13e t =-时，()1f x t =有1个实数根，当13e 4t -<<-时，()1f x t =有2个实数根，②讨论()2f x t =根的情况：因为2142t -<<-，所以()2f x t =有2个实数根，③讨论()3f x t =根的情况：因为3t >47e>，所以()3f x t =只有1个实数根，第二种情况：当47e a =时，()f t a =有2个实数根44t =-，51212t ->，则()4f x t =有2个实数根，()5f x t =有1个实数根，故当47ea =时，()()f f x a =有3个实数根；第三种情况：当47e a >时，()f t a =有一个实数根612t ->，则()6f x t =有1个实数根，综上，当470ea <<时，()()f f x a =可能有3个或4个或5个实数根；当47e a =时，()()f f x a =有3实数根；当47e a >时，()()f f x a =有1个实数根；综上，()g x 的零点个数可能是1或3或4或5．故选：D ．22．（多选题）（2023·河北唐山·开滦第二中学校考一模）若关于x 的不等式1ln ln e e ex m xm -+≥在(),m +∞上恒成立，则实数m 的值可能为（）A ．21e B ．22e C ．1eD ．2e【答案】CD【解析】因为不等式1ln ln ee e x m x m -+≥在(),m +∞上恒成立，显然0x m >>，1x m >，ln 0xm>，因此ln 1ln ln 1ee ln e ln e ln e e e xx x x x mm x x x x x m x x m m m m m-+≥⇔≥⇔≥⇔≥⋅，令()e ,0x f x x x =>，求导得()(1)0x f x x e '=+>，即函数()f x 在(0,)+∞上单调递增，ln e ln e ()(ln xxm x x x f x f m m ≥⋅⇔≥，于是ln x x m ≥，即e e xx x x m m ≥⇔≥，令(),0e x xg x x =>，求导得1()ex x g x -'=，当01x <<时，()0g x '>，当1x >时，()0g x '<，因此函数()g x 在(0,1)上单调递增，在(1,)+∞上单调递减，max 1()(1)eg x g ==，因为0x m >>，则当01m <<时，()g x 在(,1)m 上单调递增，在(1,)+∞上单调递减，1()(1)eg x g ≤=，因此要使原不等式成立，则有11em ≤<，当m 1≥时，函数()g x 在(,)m +∞上单调递减，()()()11eg x g m g <≤=，符合题意，所以m 的取值范围为1[,)e+∞，选项AB 不满足，选项CD 满足.故选：CD23．（多选题）（2023·山东·沂水县第一中学校联考模拟预测）已知函数()()()32e 04610x x f x x x x ⎧<⎪=⎨-+≥⎪⎩，其中e 是自然对数的底数，记()()()2h x f x f x a =-+⎡⎤⎣⎦，()()()3g x f f x =-，则（）A ．()g x 有唯一零点B ．方程()f x x =有两个不相等的根C ．当()h x 有且只有3个零点时，[)2,0a ∈-D ．0a =时，()h x 有4个零点【答案】ABD【解析】因为32()461(0)f x x x x =-+≥，所以2()121212(1)(0)f x x x x x x '=-=-≥，所以(0,1)x ∈时，()0f x '<，(1,)x ∈+∞时，()0f x '>所以()()()32e04610x x f x x x x ⎧<⎪=⎨-+≥⎪⎩的图像如下图，选项A ，因为()()()3g x f f x =-，令()f x t =，由()0g x =，得到()3f t =，由图像知，存在唯一的01t >，使得()3f t =，所以0()1f x t =>，由()f x 的图像知，存在唯一0x ，使00()f x t =，即()()()3g x f f x =-只有唯一零点，所以选项A 正确；选项B ，令()g x x =，如图，易知()g x x =与()y f x =有两个交点，所以方程()f x x =有两个不相等的根，所以选项B 正确；选项C ，因为()()()2h x f x f x a =-+⎡⎤⎣⎦，令()f x m =，由()0h x =，得到20m m a -+=，当()h x 有且只有3个零点时，由()f x 的图像知，方程20m m a -+=有两等根0m ，且0(0,1)m ∈，或两不等根12,m m ，1210,1m m -<<>，或121,1m m =-=（舍弃，不满足韦达定理），所以140a ∆=-=或Δ140(0)0(1)0(1)0a f f f =->⎧⎪<⎪⎨->⎪⎪<⎩即14a =或14020a a aa ⎧<⎪⎪⎪<⎨⎪-<⎪<⎪⎩，所以14a =或20a -<<，当14a =时，12m =，满足条件，所以选项C 错误；选项D ，当0a =时，由()0h x =，得到()0f x =或()1f x =，由()f x 的图像知，当()0f x =时，有2个解，当()1f x =时，有2个解，所以选项D 正确.故选：ABD.24．（多选题）（2023·全国·模拟预测）已知函数()21ln 1f x a x x =++．若当()0,1x ∈时，()0f x >，则a 的一个值所在的区间可能是（）A ．()12,11--B ．()0,1C ．()2,3D ．()24e ,e 【答案】ABC 【解析】设21t x =，因为01x <<，所以1t >，则211ln 1ln 12a x t a t x ++=-+．设()1ln 12g t t a t =-+，则()12ag t t'=-．若2a ≤，则()0g t '>，所以()g t 在()1,+∞上单调递增，所以()()120g t g >=>，则A ，B 符合题意．若2a >，则当1,2a t ⎛⎫∈ ⎪⎝⎭时，()0g t '<，所以()g t 单调递减；当,2a t ⎛⎫∈+∞ ⎪⎝⎭时，()0g t '>，所以()g t 单调递增．所以()ln 12222a a a ag t g ⎛⎫≥=-+ ⎪⎝⎭．设()()ln 11h x x x x x =-+>，则()ln 0h x x '=-<，所以()h x 在()1,+∞上单调递减，且3533ln 02222h ⎛⎫=-> ⎪⎝⎭，所以若()2,3a ∈，则()30222a a g t g h h ⎛⎫⎛⎫⎛⎫≥=>> ⎪ ⎪⎝⎭⎝⎭⎝⎭，当()0,1x ∈时，()0f x >，C 符合题意．因为()h x 在()1,+∞上单调递减，且()22e e 10h =-+<，所以若()24e ,e a ∈，则24e e ,222a ⎛⎫∈ ⎪⎝⎭，取22e a =，则()2e 022a a g h h ⎛⎫⎛⎫=<< ⎪ ⎝⎭⎝⎭，此时存在()1,t ∈+∞，使得()0g t <，即存在()0,1x ∈时，使得()0f x <，D 不符合题意．故选：ABC ．25．（多选题）（2023·全国·本溪高中校联考模拟预测）已知函数()f x 是定义在()0,∞+上的函数，()f x '是()f x 的导函数，若()()122e xx f x xf x '+=，且()e 22f =，则下列结论正确的是（）A ．函数()f x 在定义域上有极小值．B ．函数()f x 在定义域上单调递增．C ．函数()()eln H x xf x x =-的单调递减区间为()0,2．D ．不等式()12e e 4x f x +>的解集为()2,+∞．【解析】令()()m x xf x =，则()()()m x f x xf x ''=+，又()()22e xx f x xf x '+=得：()()2e xf x xf x x'+=，由()()m x f x x =得：()()()()()()()22222e xm x x m x xf x x f x m x m x f x x x x ''⋅-+--'===，令()()2e xh x m x =-得：()()2222e e e 2e 222x x x xx h x m x x x -''=-=-=⎛⎫ ⎪⎝⎭，当()0,2x ∈时，()0h x '<，()h x 单调递减；当()2,x ∈+∞时，()0h x '>，()h x 单调递增，所以()()()()2e 2e 220h x h m f ≥=-=-=，即()0f x '≥，所以()f x 单调递增，所以B 正确，A 不正确；由()()eln H x m x x =-且定义域为()0,∞+得：()()2e e e x H x m x xx-''=-=，令()0H x '<，解得02x <<，即()H x 的单调递减区间为()0,2，故C 正确．()12ee 4xf x +>的解集等价于()2e e 4x x x xf x +>的解集，设()()2e e 44xx x x m x ϕ=--，则()()222ee ee e 11424424x xx x x x m x x ϕ⎛⎫⎛⎫''=-+-=-+- ⎪ ⎪⎝⎭⎝⎭2282e e 84x x x x --=⋅-，当()2,x ∈+∞时，2820x x --<，此时()0x ϕ'<，即()x ϕ在()2,+∞上递减，所以()()()22e 0x m ϕϕ<=-=，即()2e e 4x x x xf x +<在()2,+∞上成立，故D 错误．26．（多选题）（2023·山东泰安·统考一模）已知函数()()()ln f x x x ax a =-∈R 有两个极值点1x ，2x ()12x x <，则（）A ．102a <<B ．2112x a<<C ．21112x x a->-D ．()10<f x ，()212f x >-【答案】ACD【解析】对于A ：()()()ln f x x x ax a =-∈R ，定义域()0,x ∈+∞，()()ln 120f x x ax x '=+->，函数()f x 有两个极值点1x ，2x ，则()f x '有两个变号零点，设()()ln 120g x x ax x =+->，则()1122axg x a xx-'=-=，当0a ≤时，()0g x '>，则函数()f x '单调递增，则函数()f x '最多只有一个变号零点，不符合题意，故舍去；当0a >时，12x a <时，()0g x '>，12x a>时，()0g x '<，则函数()f x '在10,2a ⎛⎫⎪⎝⎭上单调递增，在1,2a ⎛⎫+∞⎪⎝⎭上单调递减，若()f x '有两个变号零点，则102f a ⎛⎫'> ⎪⎝⎭，解得：12a <，此时x 由正趋向于0时，()f x '趋向于-∞，x 趋向于+∞时，()f x '趋向于-∞，则()f x '有两个变号零点，满足题意，故a 的范围为：102a <<，故A 正确；对于B ：函数()f x 有两个极值点1x ，2x ()12x x <，即()f x '有两个变号零点1x ，2x ()12x x <，则1212x x a<<，故B 错误；对于C ：当102a <<时，()1120f a '=->，则12112x x a <<<，即212x a >，11x ->-，则21112x x a->-，故C 正确；对于D ：()f x '有两个变号零点1x ，2x ()12x x <，且函数()f x '先增后减，则函数()f x 在()10,x 与()2,x +∞上单调递减，在()12,x x 上单调递增，121x x << ，且102a <<，()()()()1210112f x f a f x f a ⎧<=-<⎪∴⎨>=->-⎪⎩，故D 正确；故选：ACD.27．（多选题）（2023·吉林·东北师大附中校考二模）已知函数()ln xf x a a =，()()ln 1g x a x =-，其中0a >且1a ≠．若函数()()()h x f x g x =-，则下列结论正确的是（）A ．当01a <<时，()h x 有且只有一个零点B ．当1e 1e a <<时，()h x 有两个零点C ．当1e e a >时，曲线()yf x =与曲线()yg x =有且只有两条公切线D ．若()h x 为单调函数，则e e 1a -≤<【答案】BCD【解析】对A ，()ln ln(1),x h x a a a x =--令()10,ln ln(1),log (1)x x a h x a a a x a x -=∴=-∴=-，令111,164a x =-=，或111,162a x =-=1log (1)x a a x -=-都成立，()h x 有两个零点，故A 错误；对B ，1ln ln(1),x a a x -=-令1ln ,(1)ln ln ,ln(1),1x ta t x a t t x x -=∴-=∴⋅=--ln (1)ln(1)t t x x ∴=--，（1t >）.考虑ln (),()ln 10,y x x F x F x x '===+=11,()(1),e x x F a F x -∴=∴=-所以函数()F x 在1(0,e单调递减，在1(,)e +∞单调递增，1()(1),x F a F x -∴=-1ln(1)1,ln 1x x a x a x --∴=-∴=-.考虑2ln 1ln (),()0,e,x xQ x Q x x x x -'=∴==∴=所以函数()Q x 在(0,e)单调递增，在(e,)+∞单调递减，1(e),eQ =当1ln1e ()e 0,1e eQ ==-<x →+∞时，()0Q x >,所以当10ln e a <<时，有两个零点.此时1e 1e a <<，故B 正确；对C ，设21ln ,(),()e 1x ak a f x a k g x x ''=>=⋅=-，1t x =-.设切点1122111222(,()),(,()),()()(),()()(),x f x x g x y f x f x x x y g x g x x x ''∴-=--=-所以12111222()()()()()()f x g x f x x f x g x x g x ''''=⎧⎨-=-⎩.①111122222211,,11x x t a a k a k a k x x t -=∴==--。

高中数学平口单峰函数(绝对值)的一些一．平口二次函数问题去掉二次函数的的坐标系，二次函数的一切只跟一个系数有关，就是a ，一切b c ，这些系数与二次函数的形状没有任何影响.在初中的课本中提到的()22y ax y a x h k 平移变换==-+，我们将坐标轴去掉，单纯研究二次函数，解决当()[]2f x x bx c x p q ，，=++Î时，()f x c £，求c 最小值问题.由于有了绝对值，函数成为了平口型，即解决抛物线在水平跨度范围内的竖直范围.图1图2图3如图1，我们将二次函数在一个固定的纵坐标时，两个交点之间的距离叫蝶宽2m ，此时函数定顶点到蝶宽弦的距离称为蝶高n ，相对应的角叫蝶角，定义tan nma =，可以得出以下定理：①tan m a =，即蝶宽与蝶角正切值相等，蝶宽越大，蝶角越大；②以对称轴为中心，每增加m 的蝶宽，相对应的蝶高比为21:4:9::n ，增加的蝶高n 比为1:3:5::21n -；③如图2，处于同一单调区间时，最大值M 和最小值m 的差值()g x M m =-在区间距离对称轴越近时越小，离对称轴越远时越大；处于两个不同单调区间时，()g x M m =-在区间中点距离对称轴越近时越小，离对称轴越远时越大，故当仅当对称轴为中点22b p q +-=时，()()()min 22b bg x M m f q f f p f =-=--=--；综上，如图3，当0M m +=，()f x c £时，c 取得最小值，此时2p qm f+=，()()M f p f q ==.例2：设函数()2f x x ax b =++，对于任意的实数,a b ，总存在[]00,4x Î，使得()0f x t ³成立，则实数t 的解题技巧二．平口对勾函数问题对勾函数涉及极值偏移，算数平均数的中点的值不代表最值，()[],,af x x b x p q x=++Î时，()f x c £，求c 最小值问题，根据平口二次函数的推论，可以知道是()()f p f q =，如图4，求出参数a 以后再根据()0f p f+=确定参数b ；定理：当仅当a pq =时，对勾函数在区间[],p q 才能构成平口对勾函数，()f x 去最小值时取到了[],p q 的几何平均数中点.图4例3：（2018台州期末）已知()1f x x ax b x =+--，当1,22x Î时，设()f x 的最大值为(),M a b ，则(),M a b三．平口三次函数问题三次函数涉及到双峰问题，我们需要在给定的定义域内构造出单峰三次函数（即部分图像，通常是极大值到极大值等值点这一段），如下图，若[]12x ∈-，，我们可在此区间构造单峰函数.【例5】（2019•武汉调研）：已知函数()3f x x ax b =++的定义域为[1,2]-，记()f x 的最大值为M ，则M 的最小值为（）A.4B.3C.2D.秒杀秘籍：关于平口函数的万能招数例6：（2018呼和浩特期中）设函数(),,,f x ax b a b R =-Î若对于任意的实数,a b 总存在实数[]00,4x Î，使得f x m ³成立，则实数m 的取值范围为。

{}m in m ax ()()f x p x -型问题——切比雪夫最佳函数逼近理论应用一、知识点设函数()f x 在[],a b 上有二阶导数，且()f x ''在[],a b 上不变号(即恒为正或负)，则存在()f x 在[],a b 上的线性最佳一致逼近多项式()1p x 。

（其中1()p x 指1次最佳逼近，简称为一次函数、一次多项式）①理论证明与计算：略②几何意义计算：直线()1y p x =与弦MN 平行,且过线段MQ 的中点D ，其方程为221()()()()()22f a f xa x fb f a p x x b a ++-⎛⎫=+⋅- ⎪-⎝⎭说明：根据理论，Q 为()()1f x p x -的极值点，且仅有1个。

∴212()()0f x p x ''-=，而12()MN p x k '=，所以2()MNf x k '=∴Q 点的几何特征是：过点Q 的直线l MN 且l 与()y f x =相切此时：{}1min max ()()max ()()a xb a x b f x p x f x p x <<<<-=-其中的一个核心要素：会求Q 的横坐标方法1：结合几何特征，利用()2MNf x k '=方法2：结合特殊图像，可以得出的一些结论①若()f x 的图像是平口单峰函数，显然易知此时图像特征为（示意图为张口朝上）：（ⅰ）0MN k =，Q 就为()f x 极值点；（ⅱ）()()f a f b =；（ⅲ）直线l 处于正中间；（ⅳ）{}()()2min max ()()a x b f a f x f x p x <<--=②若()f x 的图像不是平口单峰函数，构造为平口单峰函数二、典例分析【2016~2017台州高三上期末】【例题1】.已知函数()()1,f x x ax b a b R x =+--∈，当1,22x ⎡⎤∈⎢⎥⎣⎦时，()f x 的最大值记为(),M a b ，则(),M a b 的最小值为_________。