当前位置：文档之家 › 控制工程根轨迹法详解教程

控制工程根轨迹法详解教程

  • 格式：ppt
  • 大小：1.47 MB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

4-4 第四节 控制系统的根轨迹分析法 自动控制原理课件

4-4 第四节 控制系统的根轨迹分析法 自动控制原理课件

时间。这些性能指标和闭环极点的关系如下：
% e 1 2 100% ectg 100%
ts
3
n
3
(为极点实部 )
n
j 1 2n
%和 的关系如下图 %
80
60
若闭环极点落在下图中红线包围
的区域中，有：
% ectg 和ts
3
40
20
0 30 60 90
上述结论也可应用于具有主导极点的高阶系统中。如下例：
是稳定的（为什么？）；
kg 64 kg 14
当 kg 195和14 kg 64 时， 系统是不稳定的。
kg 14 kg 64
kg 195
左图是用Matlab工具绘
制的。
条件稳定系统：参数在一定的范围内取值才能使系统稳定，这 样的系统叫做条件稳定系统。
下面的系统就是条件稳定系统的例子：
A B
这是一个三阶系统，从根轨迹上看出，随着kg 的增加， 主导极点越显著。所以可以用二阶系统的性能指标近似计
算。 下面计算超调量和阻尼角的关系。由于：
% ectg1 100%, 当 % 18%时解得： 60
在根轨迹图上画两条与实轴夹角为 60的直线，与根轨 迹交与A、B两点。 则A、B两点就是闭环共轭主导极点， 这时系统的超调量为18%。通过求A、B两点的坐标，可以 确定这时的根轨迹增益kg ，进而求得开环放大系数k。
[例4-12]单位反馈系统的开环传递函数为：Gk
(s)
s(s
kg 4)( s
6)
若要求闭环单位阶跃响应的最大超调量 % 18% ，试确定 开环放大系数。
[解]：首先画出根 轨迹如右。由图 可以看出：根轨 迹与虚轴的交点 为+j5,-j5，这时的 临界增益 kgp 240 当 kg 240 时， 闭环系统不稳定。

第4章控制工程根轨迹法V11

第4章控制工程根轨迹法V11

K
1
M
s s2
K 1s
[S]
K s s2
1 j 1 j 2
-2
0
1 j 1 j 2 2 2
K
N
K 1 2
4.2 绘制根轨迹的基本法则
根轨迹的分支数； 根轨迹的对称性； 根轨迹的起点与终点
实轴上的根轨迹 根轨迹的渐进线 根轨迹的起始角与终止角 分离点的坐标 根轨迹与虚轴的交点
Apj s pj
pj s pj
i 1,2, m j 1,2, n
m
n
因此有：幅角条件 zi pj 1802k 1
i 1
j 1
k 0,1,2,
m
Azi
幅值条件
K
i 1 n
1
Apj
j 1
可见，幅角条件与K 无关;
而幅值条件与K 有关，且K 由0 ~ 。
因 此 ， 复 平 面[ S ]上 所 有 满 足 幅 角 条 件 的点 都 是
二、根轨迹的对称性 因为开环极点、零点或闭环极点都
是实数或共轭复数，它们在[S]平面上的 分布对称于实轴，所以根轨迹也对称于 实轴。
[S]
三、根轨迹的起点与终点 根轨迹起始于开环极点，终止于开环
零点 如果开环零点数m小于开环极点数n ,
则有(n-m)条根轨迹终止于无穷远处。
[S]
n4
m2
nm 2 有2条根轨迹终止于处
2、K=0.5时，系统处于临界阻尼状 态；
K<0.5时，系统处于过阻尼状态； K>0.5时，系统处于欠阻尼状态；
4.1.2 根轨迹方程及幅角、幅值条件
典型反馈控制系统的闭环传递函数为
Xo Xi
s s
1

根轨迹法(自动控制原理)ppt课件精选全文完整版

根轨迹法(自动控制原理)ppt课件精选全文完整版
1 K (s z1 )( s z2 )....( s zm ) 0 (s p1 )( s p2 )....( s pn )
课程：自动控制原理
第4章 根轨迹法
➢ 以K为参变量的根轨迹上的每一点都必须满足以上方程， 相应地，称之为‘典型根轨迹方程’。
也可以写成
m
n
(s zl ) K (s pi ) 0
可见，根轨迹可以清晰地描绘闭环极点与开环增益K之间的 关系。
课程：自动控制原理
第4章 根轨迹法
2.根轨迹的基本条件
❖ 考察图示系统，其闭环传递函数为:
Y(s) G(s) R(s) 1 G(s)H(s)
闭环特征方程为：
1 G(s)H(s) 0
➢ 因为根轨迹上的每一点s都是闭环特征方程的根，所以根轨 迹上的每一点都应满足：
l 1
i 1
对应的幅值条件为：
相角条件为：
n
( s pi ) K i1
m
(s zl )
l 1
m
n
(s zl ) (s pi ) (2k 1)180
k 1,2,
l 1
i 1
课程：自动控制原理
第4章 根轨迹法
❖ 上述相角条件，即为绘制根轨迹图的依据。具体绘制方法 是：在复平面上选足够多的试验点，对每一个试验点检查 它是否满足相角条件，如果是则该点在根轨迹上，如果不 是则该点不在根轨迹上，最后将在根轨迹上的试验点连接 就得到根轨迹图。
显然，位于实轴上的两个相邻的开环极点之间一定有分离 点，因为任何一条根轨迹不可能开始于一个开环极点终止 于另一个开环极点。同理，位于实轴上的两个相邻的开环 零点之间也一定有分离点。
课程：自动控制原理
第4章 根轨迹法

自动控制原理第四章根轨迹法.

自动控制原理第四章根轨迹法.

(s z j ) pi )
m
lim
sm s
n
s
lim
1
s s nm
0
即其余的 n-m 条根轨迹终止于无穷远处，即终止于系 统的n-m个无穷大零点。
回章首 回节首
18
4-2-5 实轴上的根轨迹 实轴上根轨迹的判别方法。 在实轴上选取实验点si， 如果实验点 si 的右方实轴上的开环 零点数和极点数的总和为奇数，则 实验点 si 所在的实验段是根轨迹， 否则该实验段不是根轨迹。 图中， [-1,0]段和[-∞,-5]段是根轨迹。 而(-5,-1)段和(0,+∞)段不是根轨迹。
第四章 根轨迹法
§4-1 根轨迹法的基本概念 §4-2 绘制根轨迹图的基本法则 §4-3 控制系统根轨迹的绘制
§4-4 控制系统的根轨迹法分析
退出
.R.Evans）提出了一种在复平面上由系 统的开环极、零点来确定闭环系统极、零点的图 解方法，称为根轨迹法。 意义：可以分析系统的性能，确定系统应有的结 构和参数，也可用于校正装置的综合。
回章首 回节首
22
分离点或会合点位置的计算
(1) 重根法 数条根轨迹在复平面上某点相遇又分开，该点 必为特征方程的重根。 如两条根轨迹相遇又分开，该点为二重根。 三条根轨迹相遇又分开，该点为三重根等等。 重根的确定可以借助于代数重根法则。
回章首
回节首
23
代数重根法则
已知n次代数方程为
f ( x) x n an1x n1 ... a1x a0 0

根轨迹法是一种简便的图解方法，在控制工 程上得到了广泛的应用。
回章首
2
§4-1 根轨迹法的基本概念

第四章控制系统的根轨迹法

第四章控制系统的根轨迹法
9
应掌握的内容
180度，0度根轨迹的绘制 参数根轨迹的绘制 增加开环零、极点对根轨迹和系统性能的影响 分析系统的稳定性 分析系统的瞬态和稳态性能 对于二阶系统（及具有闭环主导共轭复数极点的高阶 系统），根据性能指标的要求在复平面上划出满足这一 要求的闭环极点（或高阶系统主导极点）应在的区域。
10
[例4-1]系统的开环传递函数为：Gk (s)
由根轨迹图可知，当0 k 0.858时，闭环系统有一对
不等的负实数极点，其瞬态响应呈过阻尼状态。当 0.858 k 29.14 时，闭环系统有一对共轭复数极点，其瞬 态响应呈欠阻尼状态。当29.14 k 时，闭环系统又有一 对不等的负实数极点，瞬态响应又呈过阻尼状态。
14
[例4-3]控制系统的结构图如下图所示。试绘制以a为参变 量时的根轨迹。
解得 k 5, 5 由图可知当k 5 时直线OB与圆相切，系统的阻 尼比 1 ，特征根为 5 j5 。
2
13
对于分离点 2.93 ，由幅值条件可知
2.93 5 2.93 k1 10 2.93 0.858
对于会合点17.07 ，有
45
17.07 5 17.0 k2 10 17.07 29.14
论过，利用根轨迹可清楚地看到开环根轨迹增益或其他参 数变化时，闭环系统极点位置及其瞬态性能的改变情况。
利用根轨迹确定系统的有关参数 对于二阶系统（及具有闭环主导共轭复数极点的高阶系 统），通常可根据性能指标的要求在复平面上划出满足 这一要求的闭环极点（或高阶系统主导极点）应在的区 域。如下页图所示，具有实部 和阻尼角 划成的左区域 满足的性能指标为：
17
例4-4（续2）
其分离回合点计算如下：
N(s) s2 3s, N ' (s) 2s 3

自动控制原理第四章根轨迹法

自动控制原理第四章根轨迹法

第四章 根轨迹法
第一节 根轨迹与根轨迹方程 根轨迹 系统的某个参数（如开环增益K）由0到∞变化时， 闭环特征根在S平面上运动的轨迹。
例： GK(S)= K/[S(0.5S+1)] = 2K/[S(S+2)] GB(S)= 2K/(S2+2S+2K) 特征方程：S2+2S+2K = 0
-P1)(S-P2)…(S-Pn)
单击此处可添加副标题
当n＞m时，只有m条根轨迹趋向于开环零点，还有（n-m）条？ m，S→∞，有: (S-Z1)(S-Z2)…(S-Zm) -1 -1 ———————-— = —— = —— P1)(S-P2)…(S-Pn) K* AK 可写成：左边 = 1/Sn-m = 0 当K=∞时，右边 = 0 K=∞（终点）对应于S→∞（趋向无穷远）. 即：有（n-m）条根轨迹终止于无穷远。
分解为：
03
例：GK(S)= K/[S(0.05S+1)(0.05S2+0.2S+1)] 试绘制根轨迹。 解： 化成标准形式： GK(S)= 400K/[S(S+20)(S2+4S+20)] = K*/[S(S+20)(S+2+j4)(S+2-j4)] K*=400K——根迹增益 P1=0，P2=-20，P3=-2+j4，P4=-2-j4 n=4，m=0
一点σa。
σa= Zi= Pi
ΣPi-ΣZi = (n-m)σa
σa= (ΣPi-ΣZi)/(n-m)
绘制根轨迹的基本法则
K*(S-Z1)(S-Z2)…(S-Zm)
—————————— = -1 (S-P1)(S-P2)…(S-Pn)

控制系统的根轨迹分析方法 自控原理 教学PPT课件

控制系统的根轨迹分析方法 自控原理 教学PPT课件

P3×
分别起始于p1, p2, p3,4，
P2
终止于无穷远。
×
-2
Im(s)
× 0 P1
Re(s)
根据规则四、实轴上存在
根轨迹是从-2到0之间。
P4×
例4-2-6
p1=0, p2= -2, p3,4= -1±j2
根据规则五、n-m=4条渐近线
与实轴交点： 渐近线相角分别为：
P3×
Im(s)
P2 ×
j5.66
×
-j5.66
例4-2-5 作
的根轨迹。
该系统 n=3 ，m=1。
有三个开环极点：
一个零点：
根据规则一、二、三： 该根轨迹有三个分支,
分别起始于p = 0(两条)和p = -12处，
有一个分支终止于z = -1,
另两个分支趋于无穷远。
× -12 -6 -4
根据规则四：
实轴上存在根轨迹是从-12到-1之间。
s1是分离点，s2是会合点。 ×
-12 -6
作完业整：的A绘-4-出7，根A轨-4-迹11，如图4-9所示。
看书p130，表4-1常规根轨迹。
●× -4 -2
图4-9
例4-2-6
分析：n=4，m=0。
根据规则一、二、三、有四个极点：
p1=0, p2= -2, p3,4= -1±j2
该根轨迹共有四个分支，
例如系统的开环零、极点分布如图。
要判断 和 之间的线段是否存
在根轨迹，取实验点
开环共轭极点和零点提供的相角 相互抵消，G(s0)的相角由实轴上的 开环零极点决定。 。
×
● ● × ××
﹣5
﹣2 ﹣1 0
处在G(s0)左边的开环零极点提供的角度 × 均为零， 相角条件由其右边的零极点决定。

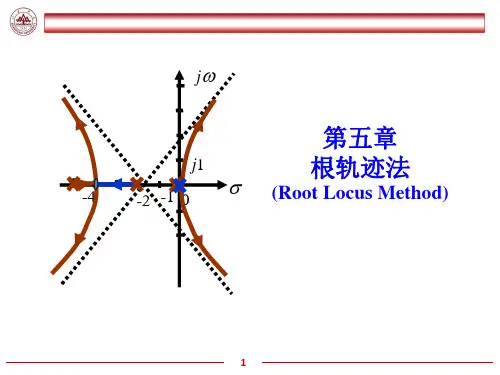
自动控制第五章根轨迹法

自动控制第五章根轨迹法
研究下图所示负反馈控制系统的一般结构： R(s) 系统的闭环传递函数为：
C(s)
G(s) H(s)
+
C ( s) G( s) ( s) R( s) 1 G ( s) H ( s)
﹣
该系统的特征方程为:
或， 上式称为系统的根轨迹方程。
7
二、根轨迹方程
系统的开环传递函数G(s)H(s)写成如下形式：
8
绘制根轨迹的基本条件
s p
根轨迹的幅值条件：
n
sz
j 1
i 1 m
i
K1
j
负反馈根轨迹的相角条件：
(s z ) (s p ) (2q 1)
j 1 j i 1 i
m
n
满足此式的根轨迹，称为1800根轨迹；
正反馈根轨迹的相角条件：
(s z ) (s p ) (2q)
根轨迹方程左边 lim
s
(s z ) (s pi )
i 1 j 1 n j
m
lim n m
s i 1
1
i
1 根轨迹方程右边 lim 0 K1 k1
(s p )
0
我们称系统有n-m个无限远零点。有限值零点加无穷远零点 的个数等于极点数。 那么，n-m支根轨迹是如何趋于无限远呢？
幅值条件确定K1

i 1 m j 1
n
s pi
j
p3
K1 12.15
11
z1
p2
p1 0

sz
第二节 绘制根轨迹的基本规则
法则1：根轨迹的分支数和对称性：根轨迹的分支数等于闭环特 征根的个数，也等于系统的阶数。闭环系统的特征根只有实根和 共轭复根两类，因此根轨迹对称于实轴。

控制工程根轨迹法详解教程23页PPT

控制工程根轨迹法详解教程23页PPT

56、书不仅是生活，而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次，但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许，为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处， 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
控制工程根轨迹法详解教程
16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以后的事， 只想现 在的事 。现在 有成就 ，以后 才能更 辉煌。
18、敢于向黑暗宣战的人，心里必须 充满光 明。 19、学习的关键--重复。
20、懦弱的人只会裹足不前，莽撞的 人只能 引为烧 身，只 有真正 勇敢的 人才能 所向披 靡。
拉
60、生活的道路一旦选定，就要勇敢地 走

(完整版)第四章根轨迹法

(完整版)第四章根轨迹法

j
8K * (1 K * )2 j
2
2
(1 K * ) K * 2 1
2
2 8K * (1 K * )2 8(2 1) 4 2 2 4 2
4
4
2 4 4 2 2
( 2)2 2
第四章 根轨迹法
自动控制原理课程的任务与体系结构
时域：微分方程 复域：传递函数 频域：频率特性
描述
控制系统
校正
时域法 复域法 频域法
评价系统的性能指标 稳定性 快速性（动态性能） 准确性（稳态性能）
分析
自动控制原理
§4 根轨迹法
§4.1 根轨迹法的基本概念 §4.2 绘制根轨迹的基本法则 §4.3 广义根轨迹 §4.4 利用根轨迹分析系统性能
• s平面上满足相角条件的点（必定满足模值条件） 一定在根轨迹上。 满足相角条件是s点位于根轨迹上的充分必要条件。
• 根轨迹上某点对应的 K* 值，应由模值条件来确定。
§4.2
m
绘制根轨迹的基本法则（1） G(s)H(s) =
K* s - z1 L s - zm s - p1 s - p2 L s - pn
K*
(s zi )
i 1 n
1
(s pj)
— 模值条件
j 1
m
n
G(s)H (s) (s zi ) (s p j ) (2k 1)
i 1
j1
— 相(s)H(s) =
K* s - z1 L s - zm s - p1 s - p2 L s - pn
§4 根 轨 迹 法
根轨迹法: 三大分析校正方法之一
特点： （1）图解方法，直观、形象。 （2）适合于研究当系统中某一参数变化时，系统性能的变化

控制系统根轨迹分析

控制系统根轨迹分析

控制系统根轨迹分析简介控制系统根轨迹分析是一种经典的控制系统稳定性分析方法。

通过分析系统的特征根轨迹，可以评估系统的稳定性、阻尼比、过渡时间等性能指标，从而设计合适的控制器来实现系统的稳定和性能要求。

根轨迹的定义控制系统的根轨迹是由系统的特征根在复平面上随参数变化所形成的轨迹。

特征根是系统传递函数的零点，它们决定了系统的动态特性。

根轨迹对应于特征根的运动轨迹，可以直观地反映系统的稳定性和相应的频率响应。

根轨迹的绘制方法步骤一：计算系统的传递函数首先，需要获得系统的传递函数。

传递函数通常是通过将系统的微分方程进行拉氏变换得到的。

传递函数是 Laplace 域中的函数，它描述了输入和输出之间的关系。

步骤二：确定系统的开环极点和零点根轨迹是由系统的特征根构成的，而特征根由系统的开环极点和零点决定。

开环极点指的是系统传递函数的分母多项式的根，而开环零点指的是系统传递函数的分子多项式的根。

通过确定系统的极点和零点，可以得到系统的特征根。

步骤三：绘制根轨迹根轨迹的绘制可以通过手工计算或数值模拟方法实现。

手工计算方法需要根据系统的传递函数进行复杂的计算，而数值模拟方法可以借助计算机软件进行自动计算和绘制。

绘制根轨迹时，需要遵循以下基本规则： - 根轨迹始于系统的零点。

如果系统有多个零点，那么根轨迹将从每个零点开始。

- 根轨迹与实轴交点的个数等于零点的个数减去极点的个数，这一性质被称为根轨迹的零点和极点计数法则。

- 根轨迹在系统的极点位置是不连续的，并且与极点的关联程度取决于极点的幅度和阶数。

根轨迹的稳定性分析通过观察根轨迹图形，可以评估控制系统的稳定性。

根轨迹的稳定性分析方法主要有以下几种：1. 判据法判据法是判断根轨迹稳定性的基本方法之一。

根轨迹的稳定性与根轨迹图形与实轴的关系有关。

如果根轨迹图形位于实轴的左侧，则系统是稳定的；如果根轨迹图形经过实轴，则系统是不稳定的。

2. Astrom法Astrom法是一种根据根轨迹图形的形态特征进行稳定性判断的方法。

自动控制课件第四章根轨迹法.ppt

自动控制课件第四章根轨迹法.ppt
第四章
根轨迹法
1
主要内容
4-1 根轨迹与根轨迹方程 4-2 绘制根轨迹的基本法则 4-3 开环零、极点变化时的根轨迹 4-4 系统闭环零、极点分布与阶跃
响应的关系 4-5 系统阶跃响应的根轨迹分析
返回主目录
2
基本要求
1.正确理解开环零、极点和闭环零、极点以及主导极 点、偶极子等概念。
2.正确理解和熟记根轨迹方程(模方程及相角方程)。 熟练运用模方程计算根轨迹上任一点的根轨迹增益 和开环增益。
f
(s zi )
K
* G
i 1 q
(s pi )
i 1
（4-5）
12
K
G
为前向通道增益，K
* G
为前向通道根轨迹增益
KG*
KG
1
2…
2
T1 T22…
（4-6）
l
(s z j)
H
(s)
K
* H
j 1 h
(s p j)
j 1
（4-7）
式中：K
* H
为反馈通道的根轨迹增益。
13
f
l
(s zi) (s z j)
G
(s)H
(s)
K
* G
K
* H
i1 q
j1 l
(s pi ) (s p j)
i1
i1
f
l
(s zi ) (s z j)
K*
i1 q
j1 h
(s pi ) (s p j)
i1
j1
（4-8）
14
闭环传递函数
f h
(s zk )
(s)
K
* G
k 1 n

控制工程基础第五章控制系统的根轨迹法

控制工程基础第五章控制系统的根轨迹法

解 系统的开环极点为0和-2，开环零点为-3。
由根轨迹的辐角条件
m
n
(s
zi)
(s
p
)
j
(2
p
1)
i1
j 1
得
(s 3) s (s 2) (2q 1)
s为复数。将s=σ+jω代入上式，则有
( j 3) ( j) ( j 2) (2q 1)
即
arctan arctan 180 arctan
a nm
30
取式中的q=0，1，2，得φa=π/3，π，5π/3。
p z 渐近线与实轴的交点为
1n [
m
] (0 1 2) 1。
a n m j1
j
i
i1
3
3条渐近线如图5-4中的虚线所示。
（3）实轴上的根轨迹位于原点与-1点之间及-2点的左边，如图中 的粗实线所示。
（4）确定分离点。
系统的特征方程为 s3 3 s2 2s 2K 0 ,即
规则4 根轨迹的渐近线。n-m条趋向无穷远的根轨迹可由渐近线决
定。
渐近线的倾角为： (2q 1) q 0,1,2,
a
nm
渐近线与实轴的交点为
n
m
p
z i
i1
j 1
a
nm
j
开环极点的实部之和 开环玲点的实部之和 开环极点数 开环零点数
【例5-3】设控制系统的开环传递函数为
G(s)H (s)
是根据系统的开环零点、极点去绘制的。
在下面的讨论中，假定所研究的变化是根轨迹增益值K0，但是当可
变参数为系统的其他参数时，这些基本法则仍然适用。这些基本法则绘
出的根轨迹，其相位遵循180°+2kπ条件的，称为180°根轨迹；其相位

控制系统根轨迹应用

控制系统根轨迹应用

控制系统根轨迹应用根轨迹法是一种用于控制系统分析与设计的有效方法。

通过观察系统根轨迹的形状和位置，我们可以对系统的稳定性、响应速度以及性能进行评估和优化。

本文将介绍控制系统根轨迹应用的原理、步骤以及实际案例，帮助读者更好地理解和应用该方法。

一、根轨迹法原理根轨迹法是利用开环传递函数的零点和极点信息来描述系统根轨迹的方法。

在复平面上，系统根轨迹与系统的极点和零点之间的关系密切相关。

根轨迹上的每一个点，都是系统极点的轨迹，表明系统在此处的稳定性、响应速度等性能。

二、根轨迹法步骤1. 确定系统的开环传递函数在应用根轨迹法之前，需要先获取系统的开环传递函数。

开环传递函数是表示系统输入与输出关系的函数，通常呈现为一个多项式的比值形式。

2. 求解系统的极点和零点根据系统的开环传递函数，可以求解系统的极点和零点。

极点和零点的数量和位置对于系统的稳定性和性能有重要影响。

3. 绘制根轨迹根据系统的极点和零点，可以绘制系统的根轨迹。

根轨迹通常表示为一条或多条曲线，反映了系统在不同极点和零点配置下的稳定性和响应特性。

4. 分析根轨迹特性通过观察根轨迹的形状和位置，可以评估系统的稳定性、响应速度以及性能。

例如，我们可以通过根轨迹分析来决定增益的合适取值，以达到系统性能的要求。

三、实际应用案例为了更好地理解根轨迹法的应用，我们以控制系统的位置环为例进行说明。

假设有一个控制系统，其开环传递函数为G(s) = K / (s+1)(s+2)。

我们希望通过根轨迹法来评估和设计该系统。

首先，我们求解系统的极点和零点。

根据开环传递函数，可以得到系统的零点为0，极点为-1和-2。

接下来，我们绘制根轨迹。

根据根轨迹的定义，我们可以确定系统在复平面上的轨迹。

在该例中，根轨迹呈现为一条从零点0开始，向左下方逐渐趋于极点-1和-2的曲线。

通过分析根轨迹的形状和位置，我们可以得出以下结论：- 系统的稳定性：根轨迹没有进入右半平面，因此系统是稳定的。

控制系统的根轨迹法分析

控制系统的根轨迹法分析

可得
s2 20s 50 0
解得
s1,2 10 5 2
因此，分离点为-2.93，会合点为-17.07。
分离角和会合角分别 为 ， 90 根轨迹为圆，如下图所示。
（2）当 2 时，阻尼角
2Hale Waihona Puke 45，表示 45角的直线为OB，其方程为
，
代入特征方程整理后得
(5 k) 10k j(2 2 5 k ) 0
解：（1）起点：有三个开环极点，所以起点为
p1 0, p2 2 j2 3, p3 2 j2 3
（2）终点：因没有有限零点，所以三条根轨迹都将趋于无穷远。
（3）实轴上的根轨迹：根轨迹存在的区间为（－∞，0］。
（4
（5
①渐近线的倾角：根据渐近线计算公式得
φα
180 (1 2μ) 2
60 ,60 ,180
例：单位反馈控制系统的开环传递函数为
K
G (s)
K
s(s 4)(s 6)
若要求闭环系统单位阶跃响应的最大超调量
σ%≤18%，试确定系统的开环增益。
解：绘出 K由零变化到∞时系统的根轨迹如图所示。当K＝17时，根轨迹在实轴
上有分离点。当K≥240时，闭环极点是不稳定的。根据σ%≤18 %的要求，求得阻尼 角应为β≤60°，在根轨迹图上作β＝60 °的射线，并以此直线和根轨迹的交点A ， B作为满足性能指标要求的闭环系统主导极点，即闭环系统主导极点为
闭环系统的极点为
s 2 1
1, 2
n
n
图中阻尼角β与阻尼比ζ的关 系为
cos1
根据根轨迹我们可以确定系统工作在根轨迹上任一点时所对应的ζ，ωn 值，再根据暂态指标的计算公式
% 12 100%

控制工程根轨迹法详解教程

控制工程根轨迹法详解教程
2、系统稳定K值：K 6 3、 因 s1, 2 j 3 可得：s3 2
j (s) 6(s 1) /(s 2)(s 2 3)
课堂练习：教材P.116的4-3。
1）
j
2）
d 1.71
j
5
2
0
1
0 .5
0
d 0.85
d1 0.29
j
3）
d 0.91
1、常规根轨迹（以增益K为参变量）
K
法则1：根轨迹起于开环极点，终于开环零点。 终点
j
K 0
1
K 如前例开环传递函数： G ( s ) s (0.5s 1)
开环零点：有限零点和无限零点。等于开环 极点数。K 0ຫໍສະໝຸດ 20起点K
法则2：根轨迹分支数等于开环极点数n ，根 轨迹是连续的并对称于实轴。
分离角：根轨迹进入分离点的切线与离开分离点切线之间的夹交。 由： j (2k 1) / l 确定。
K G 例4-1、已知单位反馈系统的开环传递函数为： ( s ) s ( s 2)(s 3)
，试绘制系统根轨迹。 解：应用上述的根轨迹绘制法则： 1）开环零、极点 2）实轴上的根轨迹 3）渐进线
2、常规根轨迹和参数根轨迹 常规根轨迹 参数根轨迹
常规根轨迹和参数根轨迹的绘制法则是相同的。 课堂练习：教材P117，4-5，4-6。 4-5： 1） s 3 2s 2 3s Ks 2 K 0 G ( s ) 4-6： 1） G ( s )
1 G( s) 0
2
20 ( s 4)(s b)
s(2s 1)
s( s 0.5)
相角方程：
( s 2) s ( s 0.5) (2k 1)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2、系统稳定K值：K 6 3、 因 s1, 2 j 3 可得：s3 2
j (s) 6(s 1) /(s 2)(s 2 3)
课堂练习：教材P.116的4-3。
1）
j
2）
d 1.71
j
5
2
0
1
0 .5
0
d 0.85
d1 0.29
j
3）
d 0.91
通过上述系统分析，可见根轨迹图与系统性能有着密切的联系。
4-1-3 根轨迹方程
1、闭环零、极点与开环零、极点之间的关系 考虑单位反馈系统，即：H ( s ) 1
R(s)
G(s) 闭环传递函数： ( s ) 1 G(s) H (s ) K 式中： G ( s ) v G0 ( s ) 则： m s m K ( i s 1) ( i s 1) i 1 ( s ) n v i 1 m G0 ( s) n s v (T j s 1) K ( i s 1) (T j s 1) j 1 i 1
解： 1） 开环传递函数为 根轨迹如图所示。 2） 闭环特征方程为：
K (1 0.5s) G( s) s( s 1)
j
K
10(1 K t s) 1 G( s) 1 0 s( s 1) s 2 s 10 10Kt s 0 10 K t s 1 2 0 s s 10 Kt* 10Kt 等效开环传递函数： 10 K t s Ge ( s ) 2 s s 10 Kt* 10Kt 根轨迹如图所示。
2、根轨迹方程
由闭环特征方程： G( s) H ( s) s v 1
(T s 1) K ( s 1) 0
j i j 1 i 1
n v
m
K ( s 1) 得： i S v (T j s 1)
j 1 i 1 n
m

K * ( s zi )
K ( s 2) s 3 2 s 2 3s
s bs 4s 4b 20 0 Ge ( s )
b( s 4) s 2 4 s 20
4-3 根轨迹法的系统设计
4-3-1根轨迹与系统性能 1、根轨迹图的信息 如右图单位反馈系统例所示： 1）稳定性
5
2
j
0
分离角：根轨迹进入分离点的切线与离开分离点切线之间的夹交。 由： j (2k 1) / l 确定。
K G 例4-1、已知单位反馈系统的开环传递函数为： ( s ) s ( s 2)(s 3)
，试绘制系统根轨迹。 解：应用上述的根轨迹绘制法则： 1）开环零、极点 2）实轴上的根轨迹 3）渐进线
30 K 0
d 0.79
sj j 6
j 6
K j 30
K 5 2 j (6 2 ) 0
也可以令 s j 代入特征方程，得：
( j )3 5( j ) 2 6 j K 0
例4-2、已知单位反馈系统开环传递函数为：G ( s )
s(2s 1)
s( s 0.5)
相角方程：
( s 2) s ( s 0.5) (2k 1)
模值方程：
K* s 2 s s 0 .5
1
设： s j 代入方程
( j 2) ( j ) ( j 0.5) (2k 1)
0 K 7
核算！
d 0.85
K计算！
2）闭环极点： 负实根 0 K 0.41 相等实根 K 0.41 共轭复根
0.41 K 7
3）系统类型和稳态误差 v 1 2、时域描述
2
1
0
j
3.12
0 .5
0
3.12
在系统同一特征方程下，根据需要，由除K以外 的参数置于K位置导出的传递函数称为等效开环传递函数。
根轨迹绘制小结：
1、根轨迹 闭环根随开环传递函数中某参数变化在S平面上 变化的轨迹。根轨迹上的点满足根轨迹方程。 开环增益K变化时的根轨迹 非K外的其他参数变化时的根轨迹
C (s )
K 2.5
K 1 K 0
s2 1 1 2K
2
j
系统特征方程： G( s) 0 1
1 K 0.5 K 0
K 1 0 s ( 1)
s 2 2s 2 K 0
2
1
0
1 2
根轨迹
K 1
K 2.5
4-1-2 根轨迹与系统性能
1
d 0.45
a (3 1 (1)) /(3 1) 0.5 5）虚轴交点 s 3 2s 2 ( K 3)s K 0 a (2k 1) / 2 / 2, / 2 由劳斯判据： K j 6, j 3 4）分离点
1 1 1 1 d d 1 d 3 d 1 试探得： d 0.45
j 1
G (s )
C (s )
分析闭环和开环零、极点的关系：
1）闭环极点由 1 G( s) s
2）闭环零点=开环零点。
v
(T s 1) K ( s 1) 0 确定。
j i j 1 i 1
n v
m
根轨迹法 3）闭环增益=开环增益。 对单位反馈系统，上述三个特点为确定闭环传递函数提供了基础。非 单位反馈不具有上述特点。
z j zi
p j zi
j 1
上述计算公式看似复杂，但很容易由相角方程获得。
法则7：根轨迹与虚轴的交点（根轨迹穿过虚轴）。
求法：1）劳斯判据（全零行），求得： K j , j . 2）在闭环特征方程中，令： s j ，然后由实部 和虚部为0，求得：K j , j . 虚轴交点 K
1、常规根轨迹（以增益K为参变量）
K
法则1：根轨迹起于开环极点，终于开环零点。 终点
j
K 0
1
K 如前例开环传递函数： G ( s ) s (0.5s 1)
开环零点：有限零点和无限零点。等于开环 极点数。
K 0
2
0
起点
K
法则2：根轨迹分支数等于开环极点数n ，根 轨迹是连续的并对称于实轴。
第四章 根轨迹法
本章主要介绍：根轨迹概念、根轨迹绘制和根轨迹应用。 4-1 根轨迹法的基本概念 开环传递函数中的某一参数从零变化到无穷时， 4-1-1根轨迹概念 闭环系统特征方程的根在S平面上变化的轨迹。 研究下述系统： 特征根为： s1 1 1 2K
R(s)
K s (0.5s 1)
i 1
m
(s p
j 1
n
1
根轨迹方程
j
)
K
K*
开环增益 根轨迹增益
相角方程：
m n
1 1 e j ( 2 k 1)
K * K in 1 ( s zi ) ( s p j ) (2k 1) i 1 j 1 k 0,1,2,... Tj
1）稳定性 因当K从0变化到无穷时，闭环根均在S左
K 2.5
K 1 K 0
2
j
1 K 0.5 K 0
半平面，所以系统稳定。
2）动态性能 当0<K<0.5时，闭环根为实根，系统为过阻尼。
2
K 1
1
0
1 2
K 2.5
当K=0.5时，系统临界阻尼，闭环根为重根。
当K>0.5后，闭环根为复根，系统为欠阻尼。 3）静态性能 在原点有一开环极点，说明系统为1型。K为静态速度误差系数。在 e 单位斜坡信号作用下的稳态误差为： ss 1 / K v .
v
闭环特征方程：1 G( s) H ( s) s
(T s 1) K ( s 1) 0
j i j 1 i 1
n v
m
1）以K为参数绘制的闭环根轨迹称为常规根轨迹；
2）以K以外参数 i , T j 绘制的根轨迹称为参数根轨迹。
以例说明： 1、等效开环传递函数 K (1 K t s) G( s) 设单位反馈系统开环传递函数： s( s 1) 试绘制：1）Kt 0.5 2） K 10 时的根轨迹。 Kt 为参数 K为参数
2 1
j
分离角
K 0
nm
(2k 1) nm
渐进线的交角： a
0
a 1,a / 2
法则5：根轨迹的分离点。两条以上根轨迹
n
K
在S平面相遇又分开的点，称为根轨迹的分离点，分离点d可 求下述方程的解：
m 1 1 d p j 1 d z i 1 i j 1 1 0 如图分离点计算： d 1 0 d d 2

j 1
m
i
K
模值方程：
*
sz
i 1 j
m
i
s p
j 1
n
1 根轨迹必须满足这两个方程。
举例：设单位反馈系统开环传递函数为： ( s ) K (0.5s 1) G 写出根轨迹方程。
s(2s 1)
解： 因： G ( s ) K (0.5s 1) 0.25K ( s 2) K * 0.25K
2、常规根轨迹和参数根轨迹 常规根轨迹 参数根轨迹
常规根轨迹和参数根轨迹的绘制法则是相同的。 课堂练习：教材P117，4-5，4-6。 4-5： 1） s 3 2s 2 3s Ks 2 K 0 G ( s ) 4-6： 1） G ( s )
1 G( s) 0
2
20 ( s 4)(s b)
K K 0 K 0