22.1.2二次函数的图象和性质

22.1.2 二次函数y=ax²的图象与性质说课稿一、教学目标1.知识与能力：•了解二次函数y=ax²的基本函数图象特点；•掌握二次函数图象的平移、伸缩和翻转变换；•理解二次函数和一次函数的区别。

2.过程与方法：•激发学生对二次函数的兴趣；•引导学生通过观察、探究并总结出二次函数y=ax²的图象特点；•通过实例分析，引导学生掌握二次函数图象的平移、伸缩和翻转变换。

3.情感态度与价值观：•培养学生观察问题、分析问题、解决问题的能力；•引导学生在学习数学的过程中培养耐心和毅力。

二、教学重点和难点1.教学重点：•二次函数y=ax²的基本图象特点；•二次函数图象的平移、伸缩和翻转变换。

2.教学难点：•引导学生通过观察、探究并总结出二次函数y=ax²的图象特点。

三、教学准备1.教学工具：•PowerPoint；•讲师笔记。

2.教学材料：•教材《人教版数学九年级上册》；•预习资料。

四、教学过程第一步：导入新知1.通过展示数学九年级上册预习资料中的图像，激发学生对二次函数的兴趣，并引出本节课的主题。

2.引导学生回顾一次函数y=ax+b的定义和性质，并引出二次函数y=ax²的定义。

第二步：展示二次函数y=x²的图象特点1.在白板上画出二次函数y=x²的图象。

2.通过观察图象，引导学生总结出二次函数y=x²的特点：•对称轴为y轴；•顶点坐标为(0, 0)；•图象开口向上。

3.引导学生思考：如果改变a的值，对图象会有什么影响？设置不同的a值进行观察和比较。

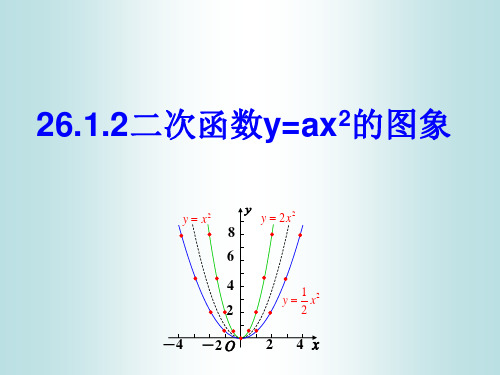
第三步：引入二次函数y=ax²的图象变换1.通过展示不同a值的二次函数y=ax²的图象，引导学生观察并比较，总结出不同a值对图象的影响：•a>1时，图象变瘦长；•0<a<1时，图象变胖矮；•a<0时，图象分别在x轴的上方和下方对称。

教 学 内 容一、探索新知：画二次函数y ＝x 2的图象． 列表：x … －3 －2 －1 0 1 2 3y ＝x 2…描点，并连线由图象可得二次函数y ＝x 2的性质：1．二次函数y ＝x 2是一条曲线，把这条曲线叫做______________． 2．二次函数y ＝x 2中，二次函数a ＝_______，抛物线y ＝x 2的图象开口______． 3．自变量x 的取值X 围是____________．4．观察图象，当两点的横坐标互为相反数时，函数y 值相等，所描出的各对应点关于________对称，从而图象关于___________对称．5．抛物线y ＝x 2与它的对称轴的交点（ ， ）叫做抛物线y ＝x 2的______． 因此，抛物线与对称轴的交点叫做抛物线的_____________． 6．抛物线y ＝x 2有____________点（填“最高”或“最低”） ． 二、例题分析例1 在同一直角坐标系中，画出函数y ＝12x 2，y ＝x 2，y ＝2x 2的图象．解：列表并填：x…－4 －3 －2 －112341．填表：开口方向顶点 对称轴有最高或最低点最值y ＝23 x 2当x ＝____时，y 有最_______值，是_y ＝－8x 22．若二次函数y ＝ax 2的图象过点（1，－2），则a 的值是___________． 3．二次函数y ＝(m －1)x 2的图象开口向下，则m____________． 4．如图，① y ＝ax 2② y ＝bx 2③ y ＝cx 2 ④ y ＝dx 2比较a 、b 、c 、d 的大小，用“＞”连接．___________________________________七、目标检测1．函数y ＝37x 2的图象开口向_______，顶点是__________，对称轴是________，当x ＝___________时，有最_________值是_________． 2．二次函数y ＝mx22 m 有最低点，则m ＝___________．3．二次函数y ＝(k ＋1)x 2的图象如图所示，则k 的取值 X 围为___________．4．写出一个过点（1，2）的函数表达式_________________． 六、教学效果追忆:。

第二十二章二次函数22.1二次函数的图像和性质22.1.1 二次函数知识点一 二次函数的定义1.二次函数的定义:一般地，形如)0a ,,(2≠++=是常数，c b a c bx ax y 的函数，叫做二次函数.2.任何一个二次函数的解析式都可化成)0a ,,(2≠++=是常数，c b a c bx ax y 的形式，因此，把)0a ,,(2≠++=是常数，c b a c bx ax y 叫做二次函数的一般式3.二次函数)0a ,,(2≠++=是常数，c b a c bx ax y 中y x ,是变量，c b a ,,是常量.自变量x 的取值范围是全体实数，b 和c 可以是任意实数，a 必须是不等于 0的实数.知识点二 实际问题中的二次函数22.1.2二次函数2ax y =的图像和性质理解 题意 分析问题中的变量和常量及它们之间的关系列函数 关系式22.1.3二次函数()k h x a y +-=2的图像和性质第一课时 二次函数k ax y +=2的图像和性质第二课时 二次函数()2h x a y -=的图像和性质第三课时 二次函数()k h x a y +-=2的图像和性质22.1.4 二次函数)0a ,,(2≠++=是常数，c b a c bx ax y 的图象和性质第一课时 二次函数c bx ax y ++=2的图象和性质知识点一 二次函数c bx ax y ++=2与()k h x a y +-=2之间的关系 利用二次函数图象平移的规律求平移后的函数的解析式，首先要把函数解析式化为顶点式:()k h x a y +-=2知识点二 二次函数c bx ax y ++=2的图象和性质 1. 二次函数c bx ax y ++=2的图象是一条抛物线，与抛物线2ax y =的形状相同，位置不同，利用配方法可以将c bx ax y ++=2转化成顶点式，即a b ac a b x a c bx ax y 442222-+⎪⎭⎫ ⎝⎛+=++= 2. 二次函数c bx ax y ++=2的性质（1）当0>a 时，抛物线开口向上，对称轴为直线a bx 2-=，顶点坐标为⎪⎪⎭⎫ ⎝⎛--a b ac ab 44,22c bx ax y ++=20>a0<a开口方向 向上 向下对称轴 直线ab x 2-= 直线ab x 2-= 顶点坐标⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22 ⎪⎪⎭⎫⎝⎛--a b ac a b 44,22 增减性当a b x 2->时，y 随x 的增大而增大；当a b x 2-<时，y 随x 的增大而减小当abx 2->时，y 随x 的增大而减小；当abx 2-<时，y 随x 的增大而增大最值当ab x 2-=时，ab ac y 442-=最小值当ab x 2-=时，ab ac y 442-=最大值知识点三 二次函数c bx ax y ++=2的图象与系数c b a ,,之间的关系 系数 图像的特征 系数的符号a开口向上 0>a 开口向下0<a b对称轴为y 轴 0=b对称轴在y 轴左侧同号b a ,对称轴在y 轴右侧 异号b a ,c经过原点0=c 与y 轴正半轴相交 0>c 与y 轴负半轴相交0<c第二课时 用待定系数法求二次函数的解析式知识点一 用待定系数法求二次函数的解析式根据已知条件确定二次函数解析式，通常利用待定系数法，用待定系数法求二次函数的解析式必须根据题目的特点，选择适当的形式，才能使解题便捷。