线性代数43二次型与对称矩阵的有定性
- 格式:ppt
- 大小:1.02 MB
- 文档页数:13

对称矩阵与二次型对称矩阵和二次型是线性代数中非常重要的概念,它们在各种数学和工程领域都有广泛的应用。
本文将介绍对称矩阵的定义和特性,以及与之相关的二次型的概念和性质。
一、对称矩阵的定义与特性在线性代数中,对称矩阵是指满足矩阵的转置等于其自身的矩阵。
具体定义如下:定义1:对称矩阵设A是一个n×n的矩阵,如果满足A^T=A,则称A为对称矩阵。
对称矩阵的一些特性如下:特性1:主对角线上的元素对称矩阵的主对角线上的元素都相等,即a_ij = a_ji。
特性2:特征值对称矩阵的特征值都是实数。
特性3:特征向量对称矩阵的特征向量对应不同特征值的特征向量是正交的。
特性4:对角化对称矩阵可以被对角化,即可以通过相似变换得到对角矩阵。
二、二次型的定义与性质二次型是对称矩阵与向量的乘积,它是一个函数,将向量映射为实数。
具体定义如下:定义2:二次型设f(x) = x^TAx是一个定义在R^n上的函数,其中A是一个n×n的对称矩阵,x是一个n维列向量。
称f(x)为二次型。
二次型有一些重要的性质:性质1:对称性二次型的矩阵A是对称矩阵,即A^T=A。
性质2:标准型对于任意二次型f(x),都存在一个正交变换,将其化为标准型。
标准型的形式为f(x) = λ_1y_1^2 + λ_2y_2^2 + ... + λ_ny_n^2,其中λ_1, λ_2, ..., λ_n为实数,y_1, y_2, ..., y_n为变量。
性质3:正定、负定与半正定二次型可以根据其对应的矩阵A的特征值判定其正定、负定与半正定。
当A的所有特征值均为正时,二次型为正定;当A的所有特征值均为负时,二次型为负定;当A的特征值既有正又有负时,二次型为不定;当A的特征值既有非负又有非正时,二次型为半正定。
三、对称矩阵与二次型的关系对称矩阵与二次型之间有紧密的联系,通过对称矩阵可以定义出二次型,同时对于任意一个二次型,都可以找到对应的对称矩阵。



一、逆序数:在一个n级排列中,如果有较大的数排在较小的数前面(<),则称与构成一个逆序,一个n级排列中逆序的总数,称为它的逆序数,记为N(*奇排序:逆序数是奇数;偶排序:逆序数是偶数(一)任意一个排序经过一个对换后奇偶性改变(二)n个数码(n>1)共有n!个排列,其中奇偶排列各占一半二、n阶行列式=(按行顺序取)n级行列式的一般项:(当)为偶数时取正号,奇数取负号)D的一般项:三、转置行列式:将行列式D的行与列互换后得到的行列式,记为或(一)将行列式转置,行列式的值不变,即(二)交换行列式的两行(列),行列式的值变号,即(三)如果行列式中有两行(列)对应的元素相同,此行列式的值为零四、用数k乘行列式的某一行(列),等于以数k乘此行列式,即:(一)如果行列式某行(列)的所有元素有公因子,则公因子可以提到行列式外面(二)如果行列式有两行(列)元素成比例,则行列式的值等于零五、如果将行列式中的某一行(列)的每一个元素都写成两个数的和,则此行列式可以写成两个行列式的和,这两个行列式分别以这两个数为所在行(列)对应位置的元素,其他位置的元素与原行列式相同,即:六、将行列式某一行(列)的所有元素同乘以数k后加于另一行(列)对应位置的元素上,行列式的值不变七、余子式:在n阶行列式D=中去掉元素所在的第i行和第j列后,余下的n-1阶行列式被称为D中元素的余子式,记为,即:代数余子式:(一)n阶行列式D=等于它的任意一行(列)的各元素与其对应代数余子式乘积的和,即:或(二)n阶行列式D=的某一行(列)的元素与另一行(列)对应元素的代数余子式乘积的和等于零,即:或(i≠s;j≠t)八、范德蒙行列式:九、克莱姆法则:线性方程组当其系数行列式D≠0时,有且仅有唯一解其中是将系数行列式中第j列元素对应地换为方程组的常数项后得到的行列式(一)如果齐次线性方程组的系数行列式D≠0,则它仅有零解(二)如果齐次线性方程组的系数行列式D=0,则方程组有非零解十、零矩阵:所有元素均为0的矩阵(行数与列数不都相同的两个零矩阵是不同的零矩阵)非负矩阵:所有元素均为非负数的矩阵十一、以数k乘矩阵A的每一个元素所得到的矩阵,称为数k与矩阵A的积,记作k A,如果A=,那么k A=十二、负矩阵:-A=十三、矩阵运算律:(一)(二)(三)(四)(五)(六)(七)(八)十四、矩阵的乘法:如果矩阵A的列数等于矩阵B的行数,则A与B的乘积C中第i行第j列的元素,等于矩阵A的第i行元素与矩阵B的第j对应元素乘积的和,并且矩阵C的行数等于矩阵A的行数,矩阵C的列数等于矩阵B的列数,即:(一)矩阵乘法一般不满足交换律(二)两个非零矩阵相乘,结果可能是零矩阵(三)矩阵乘法不满足消去律(四)矩阵乘法性质:1、2、3、4、十五、矩阵可交换:如果两矩阵A和B相乘,有AB=BA,则称矩阵A与矩阵B可交换十六、有线性方程组,系数矩阵元未知量矩阵系数矩阵十七、转置矩阵:将m*n矩阵A的行与列互换,得到的m*n矩阵,称为矩阵A的转置矩阵,记为或(一)(二)(三)(四)十八、n阶矩阵/n阶方阵:矩阵的m=n十九、方阵的幂:个(一)(二)(三)当AB可交换时,二十、方阵的行列式:由n阶矩阵(方阵)A的所有元素按原来次序构成的n阶行列式称为方阵A的行列式,记作,或(det A)(一)(二)(三)(四)二十一、特殊矩阵(一)对角矩阵:若AB为同阶对角矩阵,则kA,A+B,AB仍为同阶对角矩阵;(二)数量矩阵:数量矩阵左乘或右乘一个矩阵B,其乘积等于以数a乘矩阵B(三)单位矩阵:(四)三角形矩阵(五)对称矩阵:n阶矩阵满足1、2、数乘对称矩阵及同阶对称矩阵之和仍为对称矩阵3、当且仅当A与B可交换时,AB是对称的二十二、分块矩阵(一),(二)二十三、逆矩阵:对于n阶矩阵A,如果存在n阶矩阵B,使得AB=BA=I,那么矩阵A称为可逆矩阵,简称A可逆,并称B为A的逆矩阵,逆矩阵是唯一的,把唯一的逆矩阵记作(一)n阶矩阵可逆的充分必要条件是A非奇异,且当A可逆时,有(二)证明A可逆或证明B是A的逆矩阵,只要验证AB=I(三)逆矩阵的性质:1、若矩阵A可逆,则也可逆,且2、若矩阵A可逆,数k≠0,则kA也可逆,且3、两个同阶可逆矩阵A,B的乘积是可逆矩阵,且4、若矩阵A可逆,则A的转置矩阵5、若矩阵A可逆,则(四)(五)若AB=C,且A为非奇异,则B= C二十四、非奇异:若n阶矩阵A的行列式,则称A为非奇异的二十五、伴随矩阵:由行列式的元素的代数余子式所构成的矩阵二十六、矩阵的初等变换:(一)1、交换矩阵的两行(列)2、以一个非零的数k乘矩阵的某一行(列)3、把矩阵的某一行(列)的l倍加于另一行(列)上(二)初等矩阵:对单位矩阵I施以一次初等变换得到的矩阵(三)设,对A的行施以一次某种初等变换得到的矩阵,等于用同种的m 阶初等矩阵左乘A,对A的列施以一次某种初等变换得到的矩阵,等于用同种的n阶初等矩阵右乘A(四)任意一个矩阵经过若干次初等变换后均可以化为下面形式的矩阵:矩阵D称为矩阵A的等价标准形(五)如果矩阵A经过有限次初等变换可化为矩阵B,则称矩阵A与矩阵B等价(六)如果A为n阶可逆矩阵,则(七)n阶矩阵A为可逆的充分必要条件是它可以表示为一些初等矩阵的乘积二十七、k阶子式:从A中任取k行k列,位于这些行和列的相交处的元素,保持它们原来的相对位置所构成的k阶行列式二十八、矩阵的秩:如果A中不为零的子式的最高阶数为r,即存在r阶子式不为零,而任何r+1阶子式皆为零,则称r为矩阵A的秩,记作r(A)=r(一)满秩矩阵:r(A)=n(二)矩阵经初等变换后,其秩不变(三)二十九、增广矩阵:系数矩阵A和常数项矩阵构成的矩阵线性方程组有解的充分必要条件是齐次线性方程组有非零解的充分必要条件是→当m<n,齐次线性方程组有非零解三十、向量(一)(二)(三)(四)(五)(六)k((七)(八)三十一、向量组的线性组合线性方程组可以表示为,即常数列向量与系数列向量的线性关系,被称为方程组的向量表示,其中,于是,线性方程组是否有解,就相当于是否成立(一)如果成立,则称向量是向量组的线性组合,或称向量可以由向量组线性表示(二)向量可由向量组线性表示的充分必要条件是:以为列向量的矩阵与以为列向量的矩阵有相同的秩(三)如果组A:中每一向量都可由组B:线性表示,则称向量组A可由向量组B线性表示1、向量组A可由向量组B线性表示,向量组B又可由向量组C线性表示,则向量组A可由向量组C线性表示2、如果向量组A和向量组B可以相互线性表示,则称向量组A和向量组B等价(四)如果线性相关,而线性无关,则向量可由向量组线性表示且表示法唯一三十二、线性相关性:齐次线性方程组可以写成零向量与系数列向量的如下线性关系式:,被称为齐次线性方程组的向量形式。






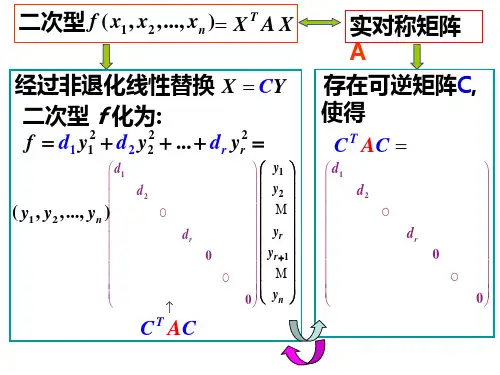
实二次型与实对称矩阵的定性分析摘 要: 本文以矩阵理论在二次型理论中的应用为基础,重点讨论了正定矩阵、负定矩 阵、半正定矩阵、半负定矩阵的若干等价命题,并给出详细的证明,得到了一些有一定价值的 结论.关键词:实二次型; 实对称矩阵; 正定矩阵1 引言数域R 上一个n 元实二次齐次多项式:j ni nj i ij n x x a x x x f ∑∑===1121),,,(Λ可表示成矩阵形式:AX X x x x f T n =),,,(21Λ其中A 是由f 的系数构成的实对称矩阵.反之,若A 是数域R 上n 阶实对称矩阵,则可得R 上的一个n 元实二次型.所以,数域R 上n 元实二次型与数域R 上n 阶实对称矩阵一一对应.因此要研究实二次型,只要研究该实二次型的矩阵即可.事实上, 实二次型的等价分类问题与矩阵的合同分类问题本质上是同一个问题.设实二次型AX X x x x f T n =),,,(21Λ,A 是实对称矩阵,若对于任意的实非零列向量X 有0>AX X T ,则称A 和f 是正定的;若对于任意的实非零列向量X 有0<AX X T ,就称A 和f 是负定的;若对于任意的实非零列向量X 有0≥AX X T ,就称A 和f 是半正定的;若对于任意的实非零列向量X 有0≤AX X T ,就称A 和f 是半负定的;若存在两个实向量),,,(21n c c c Λ和),,,(21n d d d Λ,使0),,,(21>n c c c f Λ和0),,,(21<n d d d f Λ则称f 是不定实二次型,A 便是不定的.2 实二次型性质的简单分析2.1 线性替换实二次型j ni nj i ij n x x a x x x f ∑∑===1121),,,(Λ经过非退化线性替换⎪⎪⎩⎪⎪⎨⎧++=++=++=nnn n n n n n n y c y c x y c y c x y c y c x ΛΛΛΛΛΛ112121211111化为标准形2222211n n y d y d y d +++Λ 实二次型的上述过程相当于在实二次型的矩阵表示式AX X x x x f T n =),,,(21Λ中,对于实对称矩阵A 通过寻找一个可逆矩阵C ,使⎪⎪⎪⎪⎪⎭⎫⎝⎛=n T d d d AC C O21. 2.2 正定实二次型的有关结论(1) 正定实二次型经过实满秩线性替换后仍为正定实二次型.(2) 实二次型2222211n n y d y d y d +++Λ是正定的充分必要条件是.,,2,1,0n i d i Λ=>(3) n 元实二次型),,,(21n x x x f Λ正定的充分必要条件是),,,(21n x x x f Λ 的正惯性指数为n .2. 3 负定实二次型的有关结论(1) 负定实二次型经过实满秩线性代换后仍为负定实二次型.(2)实二次型2222211n n y d y d y d +++Λ是负定的充分必要条件是.,,2,1,0n i d i Λ=<(3) n 元实二次型),,,(21n x x x f Λ负定的充分必要条件是),,,(21n x x x f Λ的 负惯性指数为n .2. 4 半正定实二次型的有关结论),,,(21n x x x f Λ的正惯性指数p 等于实二次型的秩.2. 5 半负定实二次型的有关结论),,,(21n x x x f Λ的负惯性指数q 等于实二次型的秩.3 实对称矩阵的等价条件和证明3.1 正定矩阵设)(R M A n ∈是实对称矩阵,则以下命题等价 (1) A 是正定的;(2) A 的正惯性指数等于矩阵的阶数; (3) A 合同于单位矩阵;(4) 存在可逆矩阵C ,使C C A T =;(5) A 的所有顺序主子式全大于0,特别地A 的行列式大于0.证明)2()1(⇒: 由于A 是正定矩阵,所以二次型AX X T 正定.设n 元实二次型),,,(21n x x x f Λ经过非退化线性替换变成2222211n n y d y d y d +++Λ.),,,(21n x x x f Λ正定当且仅当2222211n n y d y d y d +++Λ正定,而我们知道实二次型2222211n n y d y d y d +++Λ是正定的当且仅当n i d i ,,2,1,0Λ=>.即正惯性指数为n ,且矩阵A 的秩为n .)3()2(⇒: 设n 元实二次型),,,(21n x x x f Λ所对应的系数矩阵为A ,A 的正惯性指数为n ,则),,,(21n x x x f Λ经过非退化线性替换变为规范形式22221n y y y +++Λ,所以A 与单位矩阵合同.)4()3(⇒: A 与单位矩阵合同,则存在可逆矩阵C ,使C C EC C A T T ==. )5()4(⇒: 因为C C A T =,其中C 是可逆矩阵,所以A 是正定矩阵,则A 所对应的实二次型j n i nj i ij n x x a x x x f ∑∑===1121),,,(Λ是正定二次型.对于每一个n k k ≤≤1,令j ki kj i ij k x x a x x x f ∑∑===1121),,,(Λ,我们来证明),,,(21k x x x f Λ是k 元的正定二次型对于任意一组不全为零的实数k c c c ,,,21Λ,有0)0,,0,,,,(),,,(211121>==∑∑==ΛΛΛk j ki kj i ij k c c c f c c a c c c f .因此),,(21k x x x f Λ是正定的,有上面的推论),,,(21k x x x f Λ的矩阵的行列式n k a a a a kkk k,,2,1,01111ΛΛM O M Λ=>.这就证明了矩阵A 的顺序主子式全大于零.)1()5(⇒: 对n 作数学归纳,设j ni nj i ij n x x a x x x f ∑∑===1121),,,(Λ,其中n j i a A ij ,,2,1,),(Λ==当1=n 时,21111)(x a x f =,由条件知011>a ,所以0)(1>x f ,),,,(21n x x x f Λ是正定二次型,矩阵对应)(11a A =是正定矩阵. 假设上述论断对于1-n 元实二次型已经成立.现在来证n 元的情形,令⎪⎪⎪⎭⎫⎝⎛=----1,11,11,1111n n n n a aa a A ΛM OM Λ,⎪⎪⎪⎭⎫ ⎝⎛=-n n n a a ,1,1M α于是矩阵A 可以分块写成⎪⎪⎭⎫⎝⎛=n n T a AA ,1αα,既然A 的顺序主子式全大于零,当然1A 的顺序主子式也全大于零.由归纳假设,1A 是正定矩阵.换句话说,有可逆的1-n 级矩阵G ,使11-=n T E G A G ,这里1-n E 代表1-n 级单位矩阵. 令⎪⎪⎭⎫ ⎝⎛=1001GC 于是 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=-nn T T n nn T TT a GG E Ga A G AC C αααα1111100100 再令 ⎪⎪⎭⎫⎝⎛-=-1012αT n G E C , ⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=---10101112112ααααT n nn T T n T n T T G E a G G E GE C AC CC ⎪⎪⎭⎫ ⎝⎛-=-ααT T nnn GG a E 001于是令21C C C =就有⎪⎪⎪⎪⎪⎭⎫⎝⎛=a AC C T 11O,再两边同时取行列式a A C =2条件0>A ,因此0>a ,显然⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛a a a 111111111OOOO这就是说,A 矩阵与单位矩阵合同,因此A 是正定矩阵.3.2 负定矩阵根据定义: 设A 负定, 任给)(1,R M X n ∈,且0≠X .有0<AX X T 于是0)(>-X A X T ,同时A 也为实对称矩阵,因此得(-A )是正定矩阵.设)(R M A n ∈是实对称矩阵,则以下命题等价 (1) A 是负定的;(2) A 的负惯性指数等于矩阵的阶数;((-A )的正惯性指数即为A 的负惯性指数)(3) A 合同于(-E );(由E T A T T =-)(,即得E AT T T -=) (4) 存在可逆矩阵C ,使C C A T =-;(5) A 的所有顺序主子式k A 满足:0)1(>-k k A ,特别地0>-A .((-A )的k 阶主子式即为k k A )1(-)证明)2()1(⇒: 由于A 是负定矩阵,所以二次型AX X T 负定.设n 元实二次型),,,(21n x x x f Λ经过非退化线性替换变成.2222211n n y d y d y d +++Λ ),,,(21n x x x f Λ负定当且仅当.2222211n n y d y d y d +++Λ负定,而我们知道二次型.2222211n n y d y d y d +++Λ是负定的当且仅当n i d i ,,2,1,0Λ=<.即负惯性指数为n ,且矩阵A 的秩为n .)3()2(⇒: 设n 元实二次型),,,(21n x x x f Λ所对应的系数矩阵为A ,A 的负惯性指数为n ,则),,,(21n x x x f Λ经过非退化线性替换变为规范形式22221n y y y ----Λ,所以A 与负单位矩阵合同.)4()3(⇒: A 与负单位矩阵合同,则存在可逆矩阵C ,使C C C E C A T T -=-=)(.)5()4(⇒: 因为C C A T =-,其中C 是可逆矩阵,因此A -是正定矩阵,故A-的一切顺序主子式全大于零,从而0212222111211>---------kkk k kka a a a a a a a a ΛΛΛΛΛΛΛ,即0)1(>-k k A 且有0>-A .)1()5(⇒: 对n 作数学归纳,设j ni nj i ij n x x a x x x f ∑∑===1121),,,(Λ,其中n j i a A ij ,,2,1,),(Λ==.当1=n 时,21111)(x a x f =,由条件知011<a ,所以当01≠x 时,0)(1<x f ,因此)(1x f 是负定二次型,对应矩阵)(11a A = 是负定矩阵.假设上述论断对于1-n 元二次型已经成立.现在来证n 元的情形,令⎪⎪⎪⎭⎫⎝⎛=----1,11,11,1111n n n n a aa a A ΛM OM Λ,⎪⎪⎪⎭⎫ ⎝⎛=-n n n a a ,1,1M α于是矩阵A 可以分块写成⎪⎪⎭⎫⎝⎛=n n T a AA ,1αα,既然A 的顺序主子式A n)1(-全大于零,当然1A 的顺序主子式k k A )1(-也全大于零.由归纳假设,1A 是负定矩阵.换句话说,有可逆的1-n 级矩阵G ,使11--=n T E G A G ,这里1-n E 代表1-n 级单位矩阵.令⎪⎪⎭⎫⎝⎛=1001GC 于是 再令⎪⎪⎭⎫⎝⎛=-1012αT n G E C , ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=---10101112112ααααT n nn T T n T n T TG E a GG E GE C AC CC ⎪⎪⎭⎫⎝⎛+-=-ααT T nnn GG a E 001 令21C C C =就有⎪⎪⎪⎪⎪⎭⎫⎝⎛--=a AC C T 11O其中ααT T nn GG a a +=再两边同时取行列式a A Cn 12)1(--=由条件0)1(>-n n A ,因此0)1(12>--a n ,即0>-a ,所以0<a 且有⎪⎪⎪⎪⎪⎭⎫⎝⎛-⎪⎪⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎪⎪⎭⎫⎝⎛--a a a 111111111O O O O 这就是说,矩阵A 与负单位矩阵合同,因此A 是负定矩阵,或者说),,,(21n x x x f Λ是负定的.3.3 半正定矩阵⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=-nn T T n nn T T T a G G E Ga A G AC C αααα1111100100设)(R M A n ∈是实对称矩阵, (1) A 是半正定的; (2) 正惯性指数p 等于秩r ;(3) 存在可逆矩阵),(R n GL T ∈使得n r E AT T rT ≤⎪⎪⎭⎫⎝⎛=,000; (4) 存在实矩阵)(R M S n ∈,使得S S A T =; (5) A 的所有主子式都大于或等于0.证明)2()1(⇒:实对称矩阵A 一定合同于对角矩阵)0(),0,,0,1,,1,1,,1(n r p diag B ≤≤≤--=ΛΛΛ(其中r 为A 的秩,p 为A 的正惯 性指数)即B AT T T =,),(R n GL T ∈,若r p <,令⎪⎪⎪⎭⎫ ⎝⎛=n x x X M 1,其中1,1,01=+<=+p i x p i x 则一定有0<BX X T ,也就是:0)()(<TX A TX T ,且0≠TX .这与A 为半正定矩阵矛盾,于是得p r =.即)2()1(⇒得证.)3()2(⇒:由上面的证明得,p r =,⎪⎪⎭⎫ ⎝⎛==000)0,,0,1,,1(rTE diag AT T ΛΛ, n r ≤且),(R n GL T ∈,即)3()2(⇒得证.)4()3(⇒:由⎪⎪⎭⎫ ⎝⎛=000rT E AT T ,)(000000)()(000)(1111----⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=T E E T T E T A rrT rT 只要令)(0001-⎪⎪⎭⎫ ⎝⎛=T E S r,即得S S A T=,且易见S 为n 阶实矩阵. )1()4(⇒:若存在)(R M S n ∈,使得S S A T =,则任取)(1,R M X n ∈,有0)()(22221≥+++==n T T y y y SX SX AX X Λ,设⎪⎪⎪⎭⎫⎝⎛=n y y SX M 1,由X 的任意性可知,矩阵A 是半正定矩阵.)5()1(⇒:令⎪⎪⎪⎪⎪⎭⎫ ⎝⎛==kk k k k k i ii i i i i i i i i ii i i i i i i k k k a a a a a a a a a i i i i A A ΛΛΛΛΛΛΛΛΛ212221212111),,;,,(11 取⎪⎪⎪⎭⎫ ⎝⎛=n x x X M 1,令k j i i j x ,,,01Λ≠=.由矩阵A 的半正定性知:0≥AX X T ,也即0≥k k Tk X A X i ,记⎪⎪⎪⎭⎫ ⎝⎛=k i i k x x X M 1且k X 是任意的,于是得i k A 是半正定的,则据结论3有:⎪⎪⎭⎫⎝⎛=000rk T E T A T i ,k r ≤.两边取行列式得:02≥=i i k k T A T T A T ,因此0≥i k A ,而i k A 正是矩阵A 的任意k 阶主子式.至此)5()1(⇒得证.)1()5(⇒:考察矩阵)(A E +λ的k 阶顺序主子式)(k k A E +λ,任给0>λ.而k k k k k a a A E +++=+-Λ11λλλ,m a 为A 的全部m 阶主子式和.由结论(5)0≥m a ,又0>λ,所以0>+kk A E λ,且k 是任意的,于是)(A E +λ的所有顺序主子式大于0,从而)(A E +λ是正定的.再者,λ为任意大于0的数,即得:任给一实非 零列向量X ,必有0≥AX X T 成立.(否则,若存在实非零列向量0X ,使得000<=a AX X T,那么只要取0λ使之满足0000X X a T<<λ,就有0)(000<+X A E X Tλ 成立,与A E +λ是正定的矛盾)由此可知,A 是半正定矩阵.3.4 半负定矩阵由定义,任给)(1,R M X n ∈,有0≤AX X T从而0)(≥-X A X T ,即(A -)为半正定矩阵.比较可得如下等价判别条件: 设A 是实对称矩阵,(1)A 是半负定的;(2)A 的负惯性指数p r -等于秩r ;(A -)的正惯性指数即为A 的负惯性指数(p 是A 的正惯性指数);(3)存在可逆矩阵),(R n GL T ∈使得⎪⎪⎭⎫⎝⎛=-000)(rT E T A T ,n r ≤.也即为⎪⎪⎭⎫⎝⎛-=000rT E AT T ,n r ≤; (4)存在实矩阵)(R M S n ∈,使得S S A T =-; (5)A -的所有主子式都大于或等于0.证明)2()1(⇒:由于实对称矩阵A 一定合同于对角矩阵)0,,0,1,,1,1,,1(ΛΛΛ--=diag B ,)0(n r p ≤≤≤(其中r 为A 的秩,p n -为A 的负惯性指数.)即B AT T T =,),(R n GL T ∈,若r p r <-,则1≥p ,令11=x ,0=i x ,n i ≤≤2.则一定有0>BX X T ,也就是:0)()(>TX A TX T ,且0≠TX 这与A 为半负定矩阵矛盾,于是得p r r -=.即)2()1(⇒得证.)3()2(⇒: 由上面的证明得p r r -=,即0=p 则⎪⎪⎭⎫⎝⎛-=--=000)0,,0,1,,1(rT E diag AT T ΛΛ,n r ≤,且),(R n GL T ∈,即)3()2(⇒证.)4()3(⇒:由⎪⎪⎭⎫ ⎝⎛-=000rT E AT T ,得 )(000000)()(000)(1111----⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=-T E E T T E T A rrT rT . 只要令)(0001-⎪⎪⎭⎫ ⎝⎛=T E S r,即得S S A T=-,且易见S 为n 阶实矩阵. )1()4(⇒:若存在)(R M S n ∈,使得S S A T =-,则任取)(1,R M X n ∈,有0)()()(22221≤+++-=-=n T T y y y SX SX AX X Λ,设⎪⎪⎪⎭⎫⎝⎛=n y y SX M 1,由X 的任意性可知,矩阵A 是半负定矩阵.)5()1(⇒:设A 半负定,则A -应是半正定矩阵,由半正定矩阵的性质知A -的所有主子式都大于或等于零.)1()5(⇒:考察矩阵)(A E -λ的k 阶顺序主子式)(k k A E -λ,对于0>λ,有k k k k k a a A E +++=--Λ11λλλ,m a 为A 的全部m 阶主子式的和.由条件(5)知0≥m a ,又0>λ,所以0>-kk A E λ,且k 是任意的,于是)(A E -λ的所有顺序主子式大于0,从而)(A E -λ是正定的.再者,λ为任意大于0的数,即得任给一实非零列向量X ,必有0)(≥-X A X T 成立.(否则,若存在实非零列向量0X ,使得000<=a AX X T ,那么只要取0λ使之满足0000X X a T<<λ,就有0)(000<-X A E X Tλ成立,与)(A E -λ是正定矛盾)由此可知,A -是半正定矩阵,故A 是半负定矩阵.4 应用例1]2[实二次型32312221321),,(x x x x x x x x x f +++=是_____二次型. 解方法1:任找两点(1,0,0)和(1,0,-2)代入),,(321x x x f ,得0)0,0,1(>f ,0)2,0,1(<-f ,所以f 是不定二次型.方法2:设二次型的系数矩阵是A ,则⎪⎪⎪⎪⎭⎫⎝⎛=0212121102101A ,由033=a ,而A 中有二阶主子式0021211<,可得f 是不定二次型. 例2]2[k 为何值时才能使二次型323121232221310x x x x x kx x x x +++++为正定的.解二次型的矩阵为⎪⎪⎪⎪⎭⎫⎝⎛=12352312521k kA 由于A 有一个二阶主子式045491123231<-=-=故知无论k 为何值,二次型都不能是正定的. 例3]7[判断二次型jnnj i ini i xx x ∑∑≤<≤=+112是否为正定二次型.解该二次型的矩阵⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=1212121211212121211212121211ΛΛΛΛΛΛΛΛΛA ,A 的k 阶顺序主子式 0)211(211212121*********>-+==-k A k k ΛΛΛΛΛΛΛ,.,,2,1n k Λ= 该二次型是正定二次型.例4]2[证明设A 是实对称矩阵,证明(1)当正实数t 充分大时,A tE +是正定矩阵;(2)当正实数t 充分小时,tA E +是正定矩阵;证明(1)首先,由于A 是实对称矩阵,故对任意的实数t ,A tE +显然也是实对称矩阵.其次,令)(1t f ,)(2t f ,)(,t f n Λ为A tE +的顺序主子式,它们都是首项系数为1的实系数多项式,于是由分析学知,对充分大的正实数t ,可使n i t f i ,,2,1,0)(Λ=>.因此对充分大的正实数t ,可使A tE +为正定矩阵.(2)由于对任何正实数t ,都有)1(A E tt tA E +=+.而当t 充分小时,t 1为充分大的正数,因此由(1)知A E t+1为正定矩阵,从而tA E +为正定矩阵. 例5]1[证明若实对称矩阵A 的特征根均在闭区间[b a ,]上,则当b t >时,tE A -是负定矩阵;则当a t <时,tE A -是正定矩阵.证明设n 阶实对称矩阵A 的全部特征值为n λλ,,1Λ,),,2,1(,n i b a i Λ=≤≤λ设tE A -的全部特征值为n μμμ,,,21Λ,则t i i -=λμ,),,2,1(n i Λ=由),,2,1(,n i b a i Λ=≤≤λ知,),,2,1(,n i t b t a i Λ=-≤≤-μ当b t >时,则有0<i μ,),,2,1(n i Λ=.所以tE A -为负定的.当a t <时,则有0>i μ,),,2,1(n i Λ=.所以tE A -为正定矩阵.参考文献:[1]杨子胥. 高等代数习题集[M]. 济南:山东科技出版社,2003,390~507.[2]钱吉林. 高等代数解题精粹[M]. 北京:中央民族出版社,2002,.224,227,255.[3]北京大学数学系几何与代数教研室代数小组编. 高等代数[M]. 高等教育出版社,1987,.232~236.[4]秦少青. 二次型与实对称矩阵的正定性[J]. 晋东南师范专科学校学报,2002(5):7~59.[5]杜琦. 有关实对称矩阵的若干问题[J].华东师范大学学报,2004,56~58.[6]李伟. 二次型判别的一个方法[J]. 合肥学院学报(自然科学版),2006,12.16卷.[7]李桂荣. 高等代数习题的方法研究[M]. 香港亚太经济出版社.[8]徐丽媛,孟道冀. 关于实对称矩阵的惯性定理[J]. 2007,10.21卷10期.[9]李永乐,李正元. 数学复习全书一(理工类)[M]. 国家行政学院出版社,2006,427.[10]RogerA.Horn.Topics inMatrix Analysis[M]. 北京民邮电大学出版社,2005.Analysis for Properties ofReal Quadratic Forms and RealSymmetric MatrixesAbstract:On the basis of applications of matrix theory to quadratic form theory, this paper mainly discusses and proves in detail somepropositions equivalenteach other on positive definite matrixes, negative definite matrixes,semi-positive matrixes and semi-negative matrixes, and obtain some valuable results.Key words:Real quadratic form;Real symmetric matrix;Positive definite matrix。