当前位置：文档之家 › U634-线性代数-5.2 二次型与对称矩阵的标准形 (2)

U634-线性代数-5.2 二次型与对称矩阵的标准形 (2)

  • 格式：ppt
  • 大小：298.00 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

对称矩阵与二次型_OK

对称矩阵与二次型_OK

f a11x12 a12 x1x2 a1n x1xn a21x2 x1 a22 x22 a2n x2 xn an1 xn x1 an2 xn x2 ann xn2
2021/9/4
2
a11 a12
故“二记次型与一x个1,对x称2 ,矩阵, x一n，一则aa对2n11应”aa。n222，
化为标准形，并指出 f x1, x2 , x3 1表示何种二次
曲面 。
5 1 3
解：二次型f的矩阵
A
1
5
3, r A 2,
由于
3 3 3
5 1 3
A E 1 5 3 4 9
3 3 3
2021/9/4
12
故矩阵A的特征值为1 0, 2 4, 3 9 ，各特征值
a1n x1 a2n x2
ann xn
例如，二次型
的
A (aij )nn , x x1, x2, , xn T
f xT Ax
矩阵
。
f x12 x22 x42 2x2 x3 x2 x4
1 0 0 0
A
0 0 0
1
1
1 2
1 0 0
1 2
01
2021/9/4
2021/9/4
30
例5.7 若 f = x12 2x22 x32 2x1x2 2tx1 x3为正定二次型，
则t应满足什么条件？
解：二次型f的矩阵为
由于
1 A 1t
a11 1,
1 t
2 0
10 ,
11 A1 2
t0
a11
a12
1
1 1,
a21 a22 1 2
t 0 1 2t2 1

对称矩阵与二次型

对称矩阵与二次型

对称矩阵与二次型对称矩阵和二次型是线性代数中非常重要的概念，它们在各种数学和工程领域都有广泛的应用。

本文将介绍对称矩阵的定义和特性，以及与之相关的二次型的概念和性质。

一、对称矩阵的定义与特性在线性代数中，对称矩阵是指满足矩阵的转置等于其自身的矩阵。

具体定义如下：定义1：对称矩阵设A是一个n×n的矩阵，如果满足A^T=A，则称A为对称矩阵。

对称矩阵的一些特性如下：特性1：主对角线上的元素对称矩阵的主对角线上的元素都相等，即a_ij = a_ji。

特性2：特征值对称矩阵的特征值都是实数。

特性3：特征向量对称矩阵的特征向量对应不同特征值的特征向量是正交的。

特性4：对角化对称矩阵可以被对角化，即可以通过相似变换得到对角矩阵。

二、二次型的定义与性质二次型是对称矩阵与向量的乘积，它是一个函数，将向量映射为实数。

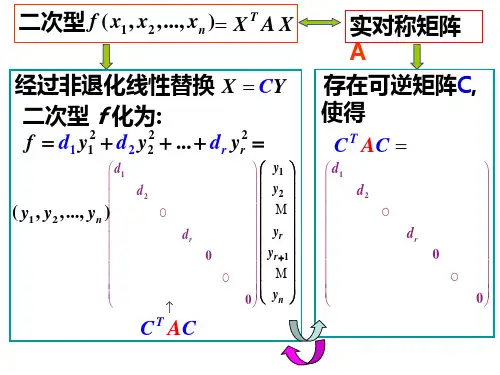
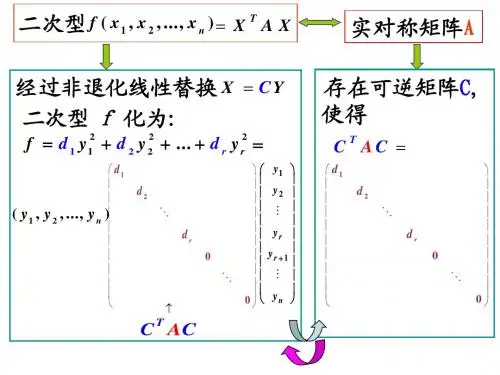
具体定义如下：定义2：二次型设f(x) = x^TAx是一个定义在R^n上的函数，其中A是一个n×n的对称矩阵，x是一个n维列向量。

称f(x)为二次型。

二次型有一些重要的性质：性质1：对称性二次型的矩阵A是对称矩阵，即A^T=A。

性质2：标准型对于任意二次型f(x)，都存在一个正交变换，将其化为标准型。

标准型的形式为f(x) = λ_1y_1^2 + λ_2y_2^2 + ... + λ_ny_n^2，其中λ_1, λ_2, ..., λ_n为实数，y_1, y_2, ..., y_n为变量。

性质3：正定、负定与半正定二次型可以根据其对应的矩阵A的特征值判定其正定、负定与半正定。

当A的所有特征值均为正时，二次型为正定；当A的所有特征值均为负时，二次型为负定；当A的特征值既有正又有负时，二次型为不定；当A的特征值既有非负又有非正时，二次型为半正定。

三、对称矩阵与二次型的关系对称矩阵与二次型之间有紧密的联系，通过对称矩阵可以定义出二次型，同时对于任意一个二次型，都可以找到对应的对称矩阵。

42二次型与对称矩阵的标准形

42二次型与对称矩阵的标准形

0 0
9
4
1 1

0 0
0
1 2
0
0 0 9
C

x x 6 x x 2 x x 例 求可逆线性替换, 化二次型 2 1 2 2 3 1 3 1 1 0 为标准形. T B C AC 解 二次型对应的矩阵为 A 1 0 3 B
其中 r 为二次型f的秩, p 为二次型f 的正惯性指标, r p 为二次型f 的负惯性指标. 且规范形由二次型 唯一决定. ' 任一实对称矩阵A 都与对角矩阵 定理 4.4 1 p 合同 , 其中 1 的个数为 1 r p －1的个数为 1 1和－1的个数共有 r 个, 1 r 为二次型的秩.
y1 z1 z 3 y1 y 3 z1 1 0 1 z 2 z y 令 y 2 y z YC 0 1 2Z 2 2 3 2 3 2 2Z 2 y z y z 3 3 3 0 0 1 3 1 1 3 C 亦即 X C Y 1 1 Z CZ | C | 2 0 1C 2Z 1 1 0 0 1
C
2 2 2 f(x , x , x ) x 3 x 4 x 2 x x 2 x x 6 x x 1 2 3 1 2 3 1 2 1 3 2 3
令
2 ( x x x ) 2 x x 4 x 1 2 3 2 3 3
2
2
2 2 2 2 y1 x x x 2 ( 2 x ) y f 4 y y 3 1 2 3 1 3 2 2 2 2 标准形唯一吗？ y 2 2x2 x3 f y y y

[全]线性代数之化二次型为标准形的方法总结[下载全]

[全]线性代数之化二次型为标准形的方法总结[下载全]

线性代数之化二次型为标准形的方法总结
线性代数考研中的两道大题是线性方程组，二次型和相似轮流来的。

由于二次型与它的实对称矩阵式一一对应的，所以二次型的很多问题都可以转化为它的实对称矩阵的问题，可见正确写出二次型的矩阵式处理二次型问题的一个基础。

二次型的标准型：
二次型的标准型
化二次型为标准型：
化二次型为标准型
用正交变换化二次型为标准型的解题步骤为：（1）把二次型表示成矩阵形式；
（2）求矩阵A的特征值及对应的特征向量；（3）对重根对应的特征向量作施密特正交化；（4）全体特征向量单位化；
（5）将正交单位特征向量合并成正交矩阵；（6）令x=Qy。

题型一：化二次型为标准型
例1：用正交变换把如下二次型化为标准型：
解题思路：按照上面用正交变换化二次型为标准型的方法来求解。

解：
总结：用正交变换把二次型化为标准型的题型是考研必考的大题，所以同学们一定要熟练掌握。

二次型与对称矩阵的标准形

二次型与对称矩阵的标准形

y1 y2
O
n
yn
例 利用正交替换法化二次型
f ( x1, x2 , x3 ) x12 2 x22 3 x32 4 x1 x2 4 x2 x3
为标准形. 解对应的
矩阵为A
1 02
2 0
1 2
2 2
23
E A
2 2
02
0 2
3
特征值 1, 2, 5
( 1)( 2)( 5)
2 3
2 3
y2 y3
1
( y1
y2
y3 )
0 0
0 2 0
0 y1
0 5
y2 y3
Q
y12 2 y22 5 y32
例 用正交替换 化二次型
f 2x12 5x22 5x32 4x1 x2 4x1 x3 8x2 x3 2 2 2
为标准形, 并写出所作的线性替换. 解 二次型对应的矩阵为
yn
实对称矩阵 A
存在可逆矩阵C, 使得
CT AC
d1
d2
O
dr
0
O
0
二次型通过非退化线性替换化成标准形 有三种方法: (一) 用配方法化二次型为标准形 (二) 用初等变换法化二次型为标准形
(三)用正交替换法化二次型为标准形
3.用正交替换法 化二次型为标准形
二次型 f ( x1, x2 ,..., xn ) X T A X 实对称矩阵A
1 2 0
二次型对应的矩阵为
A
2
2
2
2 2 1
0 2 3
3 3 3
1 0 0
Q
2 3
1
1 3
2
2 3
是正交矩阵，QT

线性代数二次形及其标准型

线性代数二次形及其标准型

5 4 2 A4 5 2
2 2 2
A的特征多项式 5 4
2
I A 4 5 2 ( 1)2( 10)
2 2 2
A的特征值为 1 1(二重)， 2 10
f xT Ax (Qy)T A(Qy) yT (QT AQ) y yT y
1
y2 1
2
y2 2
n
y2 n
线性代数 第五章
111
例4
通 过 正 交 变 换化 二 次 型
f 5 x12 5 x22 2 x32 8 x1 x2 4 x1 x3 4 x2 x3
成 标 准 形.
解 二次型矩阵
nn
f ( x) aij xi x j
x cy
i1 j1
x cy
f xT Ax
f
(
y)
d1
y2 1
d2
y2 2
dn
y2 n
.
f yT By
因为有 f xT Ax (Cy)T A(Cy) yT (C T AC ) y yT By
所以经满秩线性变换后，新旧二次型的矩阵的关系：B CT AC.
写 成 矩 阵 形 式.
解
f
(
x1 ,
x2
,
x3
)
x1 ,
x2
,
x3
0½
½
2
½ x1
32 x2
½ 32
0
x3
注
aij
a ji (i
j
)为
交
叉
项xi
x
的
j
系
数
的
一
半
，
aii为 平 方 项xi2的 系 数,

二次型的标准型和规范型

二次型的标准型和规范型



2. 正交变换法 正交变换：x Qy,其中Q为正交矩阵.
Th5.3(1)实对称矩阵A, 正交矩阵Q,使QT AQ为对角矩阵. (2)任一二次型都可经正交变换化为标准形,即 二次型f (x) xT Ax, 正交变换x Qy(Q为正交矩阵),
将其化为标准形g( y1, y2 ,, yn ) 1 y12 2 y22 n yn2 , 其中 1, 2 ,, n为A的n个特征值.


小结 : 设A为实对称矩阵, (1)求一可逆矩阵P, 使P1AP为对角矩阵. (2)求一正交矩阵Q, 使Q1AQ为对角矩阵. (3)求一可逆矩阵P,使PT AP为对角矩阵. (4)求一正交矩阵Q,使QT AQ为对角矩阵.


2. 初等变换法
准备知识： (1)化二次型f (x) xT Ax为标准形 化实对称矩阵A为对角矩阵. (2)任一方阵均可利用对等的初等行、列变换化为对角矩阵. 这里, " 对等"指的是作一次初等行变换后, 立即再作一次同种的初等列变换.
特征值的个数分别相同.


5.2 over


5.2 二次型的标准形与规范形
二次型的标准形:
二次型f (x) xT Ax 可逆 的线性变换xCy 标准形 : g( y) yT (CT AC) y d1 y12 d2 y22 dn yn2.
d1

标准形的矩阵:
B

CT
ቤተ መጻሕፍቲ ባይዱAC



d2
为正交矩阵其中qqy化为标准形将二次型其中将其化为标准形为正交矩阵正交变换二次型变换化为标准形任一二次型都可经正交为对角矩阵正交矩阵实对称矩阵标准形化为将二次型为可逆矩阵求一可逆的线性变换即可化为标准形将二次型为正交矩阵求一正交变换即可求一正交矩阵方法为对角矩阵求一可逆矩阵为实对称矩阵求一正交矩阵为对角矩阵求一可逆矩阵为对角矩阵求一正交矩阵为对角矩阵求一可逆矩阵为实对称矩阵小结aq等列变换立即再作一次同种的初指的是作一次初等行变对等这里对角矩阵的初等行列变换化为任一方阵均可利用对等为对角矩阵化实对称矩阵为标准形化二次型准备知识

5.2 二次型与对称矩阵的标准形

5.2 二次型与对称矩阵的标准形
2 f = d1 y12 + d 2 y2 + ... + d r yr2 =
d1 y1 y d2 2 ⋮ ⋱ ( y1 , y2 ,..., yn ) y dr r yr +1 0 ⋱ ⋮ yn 0 ↑
利用正交替换 正交替换法 例 利用正交替换法 化二次型
2 2 2 f ( x1 , x2 , x3 ) = x1 + 2 x2 + 3 x3 − 4 x1 x2 − 4 x2 x3
为标准形. 为标准形. 2 1 −2 0 λ −1 解 对应的 −2 2 −2 λ E − A = 2 λ − 2 A= 矩阵为
λ1 λ1 −1 λ2 λ2 T Q AQ = Q AQ = ⋱ ⋱ 定理4.14 定理4.14 λn λn ↑ A的所有特征值
存在正交矩阵Q, 存在正交矩阵Q,使得 正交矩阵
存在正交矩阵Q, 存在正交矩阵Q, 使得 正交矩阵
f ( x1 , x2 ,..., xn )= X T A X 二次型
实对称矩阵A 实对称矩阵A 存在可逆矩阵C 存在可逆矩阵C, 使得
C T AC =
d1 d2 ⋱ dr 0 ⋱ 0
经过非退化线性替换 X = CY 化为: 二次型 f 化为:
β 1 , β 2 ,α 3 两两正交
2 1 −2 2 它们单位化 单位化： 将它们单位化： 5 3 5 3 5 4 2 1 x = 15 4 = 3 5 λ3 = 10:x 3 = 3 λ1 = 1: x1 = 2 3 5 5 令 β5 5 − 2 3 1 3 −2 3 2 5 1 3 0 3 5 25 3 2 5 1 y1 1 4 2 3 x1 Q =5 3 5 3 4 2 X == 1 QY 5 3 5 3 y2 −2 经正交替换 x2 0 35 3 5 −2 y x 0 3 3 3 3 是正交矩阵. Q是正交矩阵. 1 y1 二次型化为 1 0 0 T T (Q T AQ ( y1 y2 Y3 ) Y 1 B )Yy2 y T1 − = Λ Q AQ = 0 1 0 2 y3 10 2 2

二次型和对称矩阵

二次型和对称矩阵
3 0 A4 0 0 0 6 0 0 0 0
8 3
2
0 0 , 2 3 2
0 1 P4 0 0
1 0 0 1
2 3

2 1
2 3
0 0 1 2
1 2
最后，以 －3/4 乘 A4的第三列加到第四列上, 再以－3/4 乘第三行加到第四行上，并且对 p4 的列 施行同样的初等变换，我们得到
将（5）代入（3）就得到 （6）
矩阵P称为线性变换（4）的矩阵.如果P是非奇异 的，就称（4）是一个非奇异线性变换.因为A是对 称矩阵，所以 ( PAP ) PAP PAP. PAP 也是对称矩阵.
定理9.1.1 设 aij xi x j 是数域F上的一个以A为
n
n
矩阵的n元二次型.对它的变量施行一次以P为矩 阵的线性变换后所得到的二次型的矩阵是 P AP .
3 0 A2 0 0 0 0 0 3 0 0 0 4 0 3 , 4 0 0 1 P2 0 0 1 0 0 0 0 2 1 0 0 0 0 1
把 A2 的第四列加到第二列，第四行加到第二 行，同时把 P2 和第四列加到第二列，得
c2
即F上的一个n阶对称矩阵都与一个对角形式矩阵合 同.
证 我们将利用矩阵的初等变换来证明这个定 理.回忆一下5.2里所定义的三种初等矩阵 Pi j , Di ( k )和Tij ( k )容易看出，
Pij Pi j ; Di ( k ) Di ( k ); Tij ( k ) Tij ( k )
2
(1)
2
把(1)代入一般方程得标准方程 ax cy d ,是 一个不错的方法,但是,如果类似这样的方程不是平面上 的,甚至是在任意欧氏空间中的,我们如何去化它为标准 形呢?

二次型的标准形

二次型的标准形

以 1 与2 正交，只需单位化得 p1
1 1
1 2
(1，1，0)T
，
p2
2 2
(0 ，0 ，1)T ．
②
当 3 0 时，由 Ax 0 得基础解系为 3 (1，1，0)T ，直接单位化得
p3
3 3
1 (1，1，0)T ． 2
1.1 用正交变换化二次型为标准形
1
2
（4）令
P
(
p1
，p2
，p3
应用线性代数
二次型的标准形
若二次型 f (x1 ，x2 ， ，xn ) 经过可逆线性变换 x Cy 可化为只含平方项的形式 f b1 y12 b2 y22 bn yn2 ， 则称上式为二次型 f (x1 ，x2 ， ，xn ) 的标准形， B diag(b1 ，b2 ， ，bn ) 为标准形矩阵．
T
，1
，再将
2
，3
单位化得
p2
2 2
(
2 5
，1 5
，0)T
，
p3
3 3
( 2 ， 4 ， 5 )T ． 35 35 35
1
3
（4）令
P
(
p1
，p2
，p3
)
2 3
2
3
2 5
1 5
0
2 35
4 35 5
，
x
x1 x2 x3
，
y
y1 y2 y3
，则正交变换
解
二次型
f
( x1
，x2
，x3 ) 不含平方项，令
x1 x2
y1 y1
y2 ，
y2
，即
x1 x2
1

线性代数—二次型和对称矩阵的有定性

线性代数—二次型和对称矩阵的有定性

证
( AT A)T = AT A , 故 AT A 是 n 阶对称矩阵。 因为 阶对称矩阵。
仅有零解， 又 r ( A) = n ， 可知齐次线性方程组 AX = 0 仅有零解，
所以对任意 X ≠ 0 ，必有 AX ≠ 0 ，于是 所以对
X T ( AT A) X = ( AX )T ( AX ) > 0 ,
代入二次型， 代入二次型，得 f ( 0, ⋯ ,1, ⋯ ,0) = d k ≤ 0 ，
正定矛盾。 与二次型 f ( y1 , y2 ,⋯, yn ) 正定矛盾。
2
(1) 二 次型 f ( y1 , y2 ,⋯, yn ) = d y + d y + ⋯+ d y 正定
2 1 1 2 2 2 2 n n
（2）若恒有 f ( X ) < 0 ，则称 f (X) 是负定二次型， 负定二次型， A 称为 负定矩阵 ； 称为负定矩阵 负定矩阵；
半负定二次型， （3）若恒有 f ( X ) ≤ 0 ，则称 f (X) 是半负定二次型， A 称为半负定矩阵。 称为半负定矩阵 半负定矩阵。
如果二次型不是有定的，就称为不定二次型。 如果二次型不是有定的，就称为不定二次型。 不定二次型
正定矩阵。 这是因为： 正定矩阵。 这是因为：
A 与它的转置 AT 有相同的特征值； 有相同的特征值； 矩阵
A λ ( A ) = 1 λ ( A) ; λ ( A ) = . λ ( A)
−1
∗
4
例1 判别二次型
2 2 2 f ( x 1 , x 2 , x 3 ) = x 1 + 2 x 2 + 3 x 3 − 2 x1 x 2 − 2 x 2 x 3

线性代数—二次型的标准形和规范形课件

线性代数—二次型的标准形和规范形课件
题目3
已知二次型$f(x_1, x_2, x_3) = x_1^2 + 4x_2^2 + 4x_3^2 + 4x_1x_2 - 4x_1x_3$，求其标准形。
解答部分
答案3：略
答案2：略
答案1：略
01
03 02
THANKS
感谢您的观看
详细描述
二次型可以用矩阵表示，通过将二次型中的系数排列成一个矩阵，可以方便地 研究二次型的性质和变化。这种矩阵称为二次型的矩阵表示。通过矩阵运算， 可以方便地计算二次型的值、求导数、求解方程等。
二次型的性质
总结词
二次型具有一些重要的性质，如对称性、正定性、负定性等，这些性质决定了二次型在数学和工程领域的应用价 值。
二次型用于描述物理系统的能量关系，如弹簧振荡器、谐振腔等系统的能 量形式。
二次型在物理学中用于建立数学模型，如线性方程组、微分方程等，以解 决实际问题。
二次型在经济学中的应用
01
二次型在经济学中常用于描述成本、收益和利润等 经济量之间的关系。
02
二次型用于描述经济系统的最优化问题，如生产、 消费和投资的最优配置问题。
特征值与特征向量
总结词
特征值和特征向量是二次型的重要属性 ，它们可以通过线性变换来获得。
VS
详细描述
特征值是二次型在某个特定变换下的不变 值，而特征向量则是与该特征值对应的向 量。通过特征值和特征向量，可以进一步 了解二次型的性质和结构。例如，特征值 可以用于判断二次型的正定性、负定性或 零定性，而特征向量可以用于构建二次型 的标准形。
详细描述
二次型具有对称性，即对于任意实数$x, y$，都有$f(x, y) = f(y, x)$。此外，二次型还具有正定性、负定性等性 质，这些性质决定了二次型在数学和工程领域的应用价值。例如，在物理学中，二次型用于描述物体的运动状态 和受力情况；在经济学中，二次型用于描述成本和收益的关系等。

《线性代数及其应用》第七章 对称矩阵和二次型

《线性代数及其应用》第七章 对称矩阵和二次型

1 1 1
1
( 1)2 ( 2),
所以 A 的三个特征值为:
1 2 , 2 3 1.
当 1 2 时, 解方程组 (A 1I )x 0,
即
2 1 1 x1 1 2 1 x2 0,
1 1 2 x3
解得
1
p1
1
,
1
当 2 3 1 时, 解方程组
(A 2 I )x 0,
并把它们正交化、单位化，仍记为
pi1 , pi 2 , , pini ，以这些向量为列构造矩阵
P ( p11,p12, , p1n1 ,p21,p22, , p2n2 , , ps1,ps2, ,psns ),
Λ diag(λ1, ,λ1, λ2, ,λ2 , , λs , ,λs ),
n1
n2
1 1
11
x1 x2
0,
得1p2来自1.令
1 1 P ( p1, p2 ) 1 1 ,
再求出
P 1
1 2
11
11 .
于是
An
PP1
1 2
11
11 10
0 3n
11
11
1 2
11
3n 3n
1 1
3n 3n
.
谱定理
矩阵 A 的特征值的集合有时称为 A 的谱，且下面关于 A的
特征值描述称为谱定理。
定理4 （主轴定理）
变二换次x型y设TAD是Py一y. 个，它n将 二n 次对型称x矩T阵A，x那变么换存为在不一含个交正叉交项变的量
二次型的分类
定义 一个二次型 Q 是
a.
正定的，如果对所有
x 0 ，有
Q( x )
0.

线性代数 二次型的标准型

线性代数 二次型的标准型

等价
④合同矩阵具有相同的秩.
⑤与对称矩阵合同的矩阵也是对称矩阵.
注：矩阵合同与矩阵相似是两个不同的概念
矩阵合同：
PT AP B
矩阵相似：
P 1 AP B
2021/7/3
5
注：矩阵合同与矩阵相似是两个不同的概念
A 1 1 ,B 1 9
则存在可逆矩阵
P 1 3 , 使得A与B合同；
上述定理可等价的描述为： 对任意的对称矩阵A，存在可逆矩阵P,使得
d1
PT
AP
d2
dn
二、矩阵的合同
定义： 设A、B均为n阶方阵，若存在可逆矩阵P，使得
PT AP B
则称A与B合同，记作：
AB
2021/7/3
4
注：矩阵的合同其实是一种特殊的等价。
合同具有如下性质：
①反身性 ②对称性 ③传递性
0 1
0 0
1 0
3 1
P
0 0
1 0
3 1
2021/7/3
9
PT AP D
1
1
D 1 4 D 1 1 规范形
Q
1
1
1
2
QT DQ D
QPT AQP D
注：对称矩阵每施行一次行列对称初等变换仍是对称矩阵
2021/7/3
10
f x1, x2 , x3 x12 2x1x2 2x1x3 3x22 6x2 x3
解： f x1, x2 , x3 x12 2x1 x2 x3 3x22 6x2 x3
x1 x2 x3 2 x2 x3 2 3x22 6x2 x3
x1 x2 x3 2 4 x22 2x2 x3 x32 3x32
注： 二次型的标准形（规范形）对角阵

第26节二次型与对称矩阵

第26节二次型与对称矩阵

2. 正交矩阵的性质 (1) 若 Q 为正交矩阵， 为正交矩阵，则其行列式的值为1 则其行列式的值为1或 −1 ； 若 Q为正交矩阵， 为正交矩阵，则 QT Q = I ; 证： 因为 证毕. 证毕. (2) 若 Q为正交矩阵， 为正交矩阵，则 Q 可逆， 可逆，且 Q −1 = Q T ; 可逆. 证： 由性质1 由性质1可知， 可知，正交阵
1 0 0 P = (η1 ,η 2 ,η 3 ) = 1 2 0 1 2 − 1 2 0 1 2
2 0 0
使得 P −1 AP = 0 4 0 . 0 0 4
用施密特正交化方法，将向量组 例1 用施密特正交化方法，
a1 = (1,1,1,1)T , a2 = (1, −1, 0, 4)T , a3 = (3, 5,1, −1)T
正交规范化. 正交规范化. 解：β 1 = a1 = (1,1,1,1)T ,
β 2 = α2 − α 2T β 1 4 β = (1, −1, 0, 4)T − (1,1,1,1)T β 1T β 1 1 4
0 1 0
0 0 1
特征向量是正交的 特征向量是正交的. 是正交的. <定理3> 定理3> 设 A为实对称矩阵， 为实对称矩阵，则存在正交矩阵 Q , 使 Q −1 AQ 为对角矩阵. 为对角矩阵.
所以它是正交矩阵.
2. 利用正交矩阵将对称矩阵对角化的方法 根据上述结论， 根据上述结论，利用正交矩阵将对称矩阵化为 对角矩阵 对角矩阵， 其具体步骤为： 矩阵，其具体步骤为 1) 求 A的特征值； 的特征值； 2) 由 (λi I − A) x = 0 ，求出 A的特征向量； 的特征向量； 3) 将特征向量正交化； 将特征向量正交化； 4) 将特征向量单位化. 将特征向量单位化.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

可见
对矩阵
A I
施以相应于右乘 P1
P2
Ps 的初等列变
换 再对 A 施以相应于左乘 P1T P2T PsT 的初等行变换 矩阵
A变为对角矩阵 单位矩阵I就变为所要求的非奇异矩阵C
1 1 1 例 2 求可逆矩阵 C 使 CTAC 为对角矩阵 其中A1 2 2
1 2 1
解解
AIAI11111111
为对角形(称这个对角矩阵为A的标准形) 即任何一个对称矩 阵都与一个对角矩阵合同
例 1 求一非奇异矩阵 C 使 CTAC 为对角矩阵 0 1 1
A 1 0 2
1 2 0
(二)用初等变换法化二次型为标准形
当C是非奇异矩阵 且CTAC为对角矩阵时 则有
CI P1P2 Ps (其中Pi(i1 2 s)是初等矩阵) CTACPsT P2TP1TA P1P2 Ps
1 0
11
1 1 1 例 2 求可逆矩阵 C 使 CTAC 为对角矩阵 其中A1 2 2
1 2 1
解
AI 1111
1 2 2 0
1102
1 1 1 1
011100110011
0 1 1 1
00010011 0111001100110011
0001
00
1 0
10
00
1 0
0100
1 0
1 1 1
例 2 求可逆矩阵 C 使 CTAC 为对角矩阵 其中A1 2 2 1 2 1
例3 求一非退化线性变换 化二次型2x1x22x1x34x2x3为 标准形
例 4 用正交变换把下面的二次型化为标准形 并写出所 作的正交变换
f (x1, x2, x3) 2x12 4x1x2 4x1x3 5x22 8x2 x3 5x32
11
00
0100 0101 11
因此
1 1 0
1 0 0
C 00
1 0
11
CTAC 00
1 0
01
例3 求一非退化线性变换 化二次型2x1x22x1x34x2x3为 标准形
0 1 1 解 此二次型的矩阵为A 1 0 2
1 2 0
因为
AI 0111
1 0 2 0
0021 0021
0 1/ 2
11 22 22 00
1102110211111111
00 11 11 11
00110011
0000
11 00
1010
0000
11 00
0101
00110011
00 11 11 11
00110011
0000
11 00
0101
0011
0 1 1 1
0001
00
1 0
11
0011
0 1 0 1
0001
00
将二次型化为平方项的代数和的形式后 如果有必要 可 重新安排变量的次序(这也是一个非退化线性变换)使这个标 准形化为以下形状
d1x12
d
p
x2p
d
x2
p1 p1
其中di0 (i1 2 r)
通过非退化线性替换
dr xr2
xi
1 di
yi (i 1,
2,
, r)
x j y j ( j r 1, r 2, , n)
§52 二次型与对称矩阵的标准形
(一)用配方法化二次型为标准形 (二)用初等变换法化二次型为标准形 (三)用正交变换法化二次型为标准形 (四)二次型与对称矩阵的规范形
(一)用配方法化二次型为标准形
定理51 任何一个二次型都可以通过非退化线性变换化为标准形
定理52 对任意一个对称矩阵A 存在一个非奇异矩阵C 使CTAC
2 2 2 解 二次型的矩阵为 A 2 5 4
2 4 5
求得A的特征值为121 310
求出使A相似于对角矩阵 因此 作正交变换xQy 就可
的正交矩阵
以使二次型化为标准形
2 5
5
2 15
5
1 3
Q
54 5 15
5
2 3
0
1 3
5

2 3
f y12 y22 10y32
(四)二次型与对称矩阵的规范形
说明 二次型的正惯性指标也称为二次型矩阵的正惯性指标 二次型的负惯性指标也称为二次型矩阵的负惯性指标
定理54
凡二次型都可通过非退化线性变换化为规范形 且规范
形是由二次型本身决定的唯一形式 与所作的非退化线性变
换无关
正惯性指标和负惯性指标
把规范形中正项的个数p称为二次型的正惯性指标 负项
个数qrp称为二次型的负惯性指标 其中r是二次型的秩
定理53 对于二次型f(x)xTAx 一定存在正交矩阵Q 使得经过正
交变换xQy后能够把它化为标准形
f 1y12 2 y22 n yn2 其中1 2 n是二次型f(x)的矩阵A的全部特征值
例 4 用正交变换把下面的二次型化为标准形 并写出所
作的正交变换
f (x1, x2, x3) 2x12 4x1x2 4x1x3 5x22 8x2 x3 5x32
0 1/ 2
2400
00
1 0
01
01
1/ 2 0
11
1 所以C 0
0
1/ 2 1/ 2 0
2 1 |C|10
1
令
x1 z1 (1/ 2)z2 2z3 x2 z1 (1/ 2)z2 z3
x3
z3
代入原二次型可得标准形
f 2z12 (1/ 2)z22 4z32
(三)用正交变换法化二次型为标准形
二次型又化为
y12
y
2 p
y
2 p1
yr2
这种形式的二次型称为原二次型的规范形
定理54 凡二次型都可通过非退化线性变换化为规范形 且规范
形是由二次型本身决定的唯一形式 与所作的非退化线性变 换无关 正惯性指标和负惯性指标
把规范形中正项的个数p称为二次型的正惯性指标 负项 个数qrp称为二次型的负惯性指标 其中r是二次型的秩
定理55
合同的对称矩阵具有相
A为任意对称矩阵 如果 同的正惯性指标和秩
Ip 0 0
It 0 0
CT AC 0
0
Irp 0
0
0
及 QT AQ 0 0
I r t 0
0 0
CQ |C|0 |Q|0 则pt
作业 5.2：
例 1 求一非奇异矩阵 C 使 CTAC 为对角矩阵
0 1 1
A 1 0 2 1 2 0