下载文档原格式
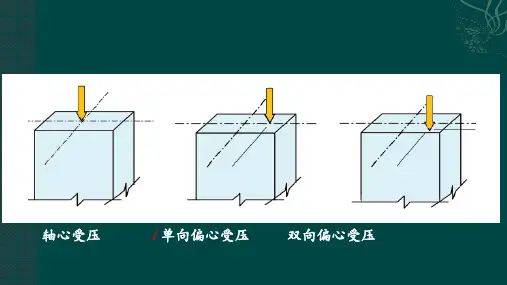
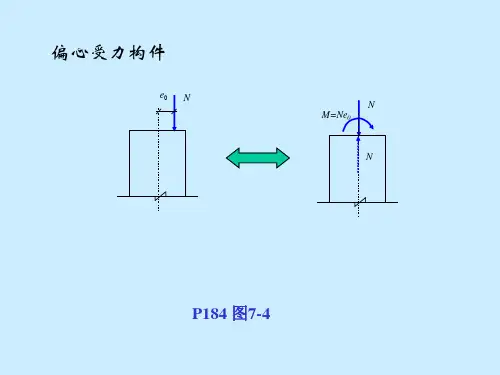
第六章 偏心受力构件§6.1 偏心受力构件的特点及截面形式从偏心受力构件的特点来看，边缘很容易达到设计强度，若按边缘达塑性视为强度极限很不经济，若按全截面达塑性，又会产生很大变形，因此与受弯构件相似，部分发展塑性。
（截面高度的4/1~8/1）§6.2 偏心受力构件的强度nyy y nx x x n W M W M A Nγγ±±≤f y x ,M M ——两个主轴方向的弯矩y x ,γγ——两个主轴方向的塑性发展因数，如工字形，x γ=1.05,y γ=1.20需要计算疲劳的拉弯、压弯构件，宜取 1.0y x ==γγ§6.3 实腹式偏心压杆的整体稳定一．弯矩作用平面内的稳定在弯矩作用平面内失稳属第二类稳定，偏心压杆的临界力与其相对偏心率ρεe =有关，A W =ρ为截面核心矩，ρεe =大则临界力低。
通常采用的理论为压溃理论。
即：根据临界状态内外力平衡条件和变形调条件导出截面平均应力和杆中挠度的关系。
0),m cr =y σφ（cr mm cr 0),(σσφ−→−=dy y d如此算得的平均应力值使变形过大，限制截面塑性发展在截面高度的)4/1~8/1(，采用弹性相关公式加以修正。
1)1(E s 0s=-⋅++xN N M e N M N N0e ——偏心距2x2E πλEAN x =——欧拉临界力1x1x y 1x s y s y I W f W M Af N ===，， 1y ——受压最大点距中和轴距离xN NE 1-——弯矩放大因数（偏心矩增大因数） 考虑部分塑性发展，令p M 代替s M 则:1)1(E y 1x x 0s=-⋅++xN Nf W e N M N N γ当M =0时，即为具有初始偏心0e 的轴心压杆，设其为x N （实际的轴心受力稳定承载力），则由上式可得：AWN N N N N N e Ex x 1x x x x E x s 0))((γ⋅⋅--=代回上式得：1)1(sxE y 1x x x=⋅-+N N N N f W MN N x γ上式变为，，x sxcr x ϕσ=⋅=N N A N y E x 1x x x )1(f N NW MAN x=-+ϕγϕ由此式算得结果与实际有出入，经过修正：)0.81(E 1x x mx x xN NW MAN -⋅+γβϕ≤f轴心受力构件中的考虑1000l 的初挠度，而偏压构件中的0e 很大，故此式误差就应主要在这里。
