下载文档原格式
6钢筋混凝土偏心受力构件承载力计算钢筋混凝土偏心受力构件是一种常用的结构形式，常见于各种建筑和桥梁工程中。
在设计和施工过程中，对其承载力进行准确计算是十分重要的。
本文将介绍钢筋混凝土偏心受力构件的承载力计算方法，包括偏心受压构件和偏心受拉构件的计算。
首先，我们来介绍偏心受压构件的承载力计算方法。
偏心受压构件是指受压钢筋与截面重心之间有一个偏心距的构件。
其计算工作主要分为两个步骤：截面计算和偏心距计算。
1.截面计算：确定混凝土和钢筋的受力状态。
首先，计算构件的受拉区和受压区的面积，分别记为A_s和A_c。
其次，计算出受拉区的应力，记为σ_s。
然后，计算出受拉区的抗拉钢筋面积As'，使得其能够承受施加在构件上的最大拉力。
最后，通过平衡条件，计算出混凝土的受压区的应力σ_c。
2.偏心距计算：确定偏心距的大小。
偏心距的计算与混凝土和钢筋的受力状态有关。
在受力状态已知的情况下，可以通过拉力平衡方程计算出偏心距的大小，即：e=(α*As'*σ_s-As*σ_c)/b*f_c其中，e为偏心距，α为抗拉钢筋的应力分配系数，As为受压区的钢筋面积，b为构件宽度，f_c为混凝土的抗压强度。
偏心距的计算对于后续的承载力计算非常重要。
当偏心距大于受压区最大尺寸的一半时，构件发生弯曲破坏；当偏心距小于受压区最大尺寸的一半时，构件发生压碎破坏。
下面，我们来介绍偏心受拉构件的承载力计算方法。
偏心受拉构件是指受拉钢筋与截面重心之间有一个偏心距的构件。
其计算工作同样分为两个步骤：截面计算和偏心距计算。
1.截面计算：确定混凝土和钢筋的受力状态。
首先，计算构件中混凝土的受拉面积A_c，然后计算受拉区的应力σ_c。
其次，计算出能够承受施加在构件上的最大拉力的钢筋面积A_s'。
最后，通过平衡条件，计算出抗拉钢筋的应力σ_s。
2.偏心距计算：确定偏心距的大小。
偏心距的计算方法同样适用于偏心受拉构件，即使用拉力平衡方程计算出偏心距e，公式如下：e=(A_s*σ_s-A_c*σ_c)/(b*f_c)在计算偏心受拉构件的承载力时，需要注意偏心距的大小。
矩形截面钢筋混凝土偏心受压构件的正截面抗压承载力的计算程序一、引言矩形截面钢筋混凝土偏心受压构件在土木工程中有着广泛的应用，其正截面抗压承载力的计算是结构设计中的重要环节。
本文将详细介绍矩形截面钢筋混凝土偏心受压构件的正截面抗压承载力的计算程序，以期为工程实践提供参考。
二、计算原理矩形截面钢筋混凝土偏心受压构件的正截面抗压承载力计算基于材料力学、混凝土力学和钢筋力学的基本原理。
通过分析截面的应力分布，结合混凝土和钢筋的应力-应变关系，推导出构件的承载力计算公式。
三、计算步骤1. 确定构件尺寸：根据设计要求和结构布置，确定矩形截面钢筋混凝土偏心受压构件的截面尺寸、配筋等参数。
2. 确定偏心距：根据荷载分布情况，确定作用在构件上的偏心距。
3. 计算混凝土弯矩：根据偏心距和截面尺寸，计算混凝土的弯矩。
4. 计算钢筋拉力：根据混凝土弯矩和配筋情况，计算钢筋的拉力。
5. 确定承载力：根据混凝土和钢筋的应力-应变关系，结合截面的应力分布，计算出构件的正截面抗压承载力。
6. 考虑其他因素：根据具体情况，考虑其他可能影响承载力的因素，如施工质量、环境条件等。
四、案例分析以某框架结构中的矩形截面钢筋混凝土偏心受压构件为例，介绍正截面抗压承载力的计算过程。
该构件尺寸为200mm x 400mm，采用C30混凝土，HRB400级钢筋。
作用在构件上的偏心距为30mm。
1. 混凝土弯矩计算：根据偏心距和截面尺寸，采用材料力学中的弯矩公式计算混凝土弯矩。
弯矩公式为：M = eyfb，其中e为偏心距，y为截面重心到偏心方向的截面边缘的距离，f为混凝土的抗压强度设计值，b为截面宽度。
代入已知参数，得到混凝土弯矩为3.68 x 106 Nmm。
2. 钢筋拉力计算：根据混凝土弯矩和配筋情况，采用结构力学中的弯矩平衡公式计算钢筋的拉力。
弯矩平衡公式为：M = fyAs，其中fy为钢筋的抗拉强度设计值，As为钢筋的截面面积。
代入已知参数，得到钢筋拉力为2.29 x 104 N。
第七章钢筋混凝土偏心受力构件承载力计算本章的基本要求：1、了解偏心受压构件的受力特性；掌握两类偏心受压构件的判别方法；2、熟悉偏心受压构件的二阶效应及计算方法；3、掌握两类偏心受压构件正截面承载力的计算方法；4、了解双向偏心受压构件正截面承能力计算；5、掌握偏心受拉构件的受力特性及正截面承载力计算；6、掌握偏心受力构件斜截面受剪承载力计算。
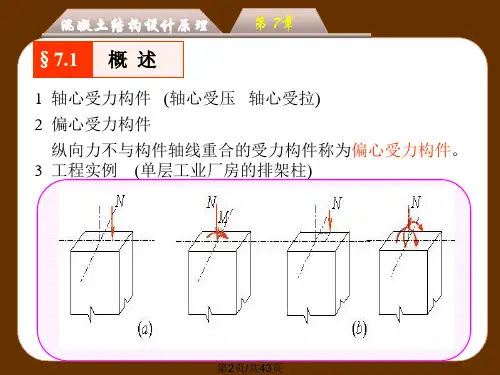
§7-1 概述偏心受力构件：偏心受力构件是指纵向力N作用线偏离构件轴线或同时作用轴力及弯矩的构件，包括偏心受压构件见图7-1（a）、（b）和偏心受拉构件见图7-1（c）、（d）。
图7-1 偏心受力构件受力形态工程中大多数竖向构件（如单层工业厂房的排架柱，多层及高层房屋的钢筋混凝土墙、柱等）都是偏心受压构件；而承受节间荷载的桁架拉杆、矩形截面水池的池壁等，则属于偏心受拉构件。
钢筋混凝土偏心受压构件多采用矩形截面，截面尺寸较大的预制柱可采用工字形截面和箱形截面，公共建筑中的柱多采用圆形截面。
偏心受拉构件多采用矩形截面。
图7-2 偏心受力构件的截面形式§7-2 偏心受压构件正截面承载力计算一、偏心受压构件正截面的破坏特征（一）破坏类型大量试验表明：构件截面中的符合平截面假定，偏压构件的最终破坏是由于混凝土压碎而造成的。
其影响因素主要与偏心距的大小和所配钢筋数量有关。
通常，钢筋混凝土偏心受压构件破坏分为2种情况1、受拉破坏：当偏心距较大，且受拉钢筋配置得不太多时，发生的破坏属大偏压破坏。
这种破坏特点是受拉区、受压区的钢筋都能达到屈服，受压区的混凝土也能达到极限压应变，如图7—2a 所示。
2、受压破坏：当偏心距较小或很小时，或者虽然相对偏心距较大，但此时配置了很多的受拉钢筋时，发生的破坏属小偏压破坏。
这种破坏特点是，靠近纵向力那一端的钢筋能达到屈服，混凝土被压碎，而远离纵向力那一端的钢筋不管是受拉还是受压，一般情况下达不到屈服。
如图7—2b 、c 所图7-3 受拉破坏和受压破坏时的截面应力（二）界限破坏及大小偏心受压的分界1、界限破坏在大偏心受压破坏和小偏心受压破坏之间，从理论上考虑存在一种“界限破坏”状态；当受拉区的受拉钢筋达到屈服时，受压区边缘混凝土的压应变刚好达到极限压应变值cu ε。
这种特殊状态可作为区分大小偏压的界限。
二者本质区别在于受拉区的钢筋是否屈服。
2、大小偏心受压的分界由于大偏心受压与受弯构件的适筋梁破坏特征类同,因此,也可用相对受压区高度比值大小来判别。
1b ys cu 1f E βξε=+当 b ξξ≤ 时，截面属于大偏压；当b ξξ>时,截面属于小偏压;当b ξξ=时，截面处于界限状态。
（三）弯矩和轴心压力对偏心受压构件正截面承载力的影响偏心受压构件是弯矩和轴力共同作用的构件。
弯矩与轴力对于构件作用彼此之间相互牵制，对于构件的破坏很有影响。
如对给定材料、截面尺寸和配筋的偏心受力构件，在达到承载力极限状态时，截面承受的轴力与弯矩具有相关性，即构件可以在不同的轴力和弯矩组合下达到承载力极限状态。
具体讲，在大偏压破坏情况下，随着构件轴力的增加，构件的抗弯能力提高，但在小偏心受压破坏情况下，随着构件轴力的增加，构件的抗弯能力反而减小，而在界限状态时，一般构件能承受弯矩的能力达到最大值（图7－4）。
﹡在小偏心受压情况下，随着轴向压力的增大，截面所能承担的弯矩反而降低。
图7-4 N u ~M u 相关曲线（四）附加偏心距由于工程中实际存在着荷载作用位置的不定性，混凝土的不均匀性及施工的偏差等因素，都可能产生附加偏心距。
因此，在偏心受压构件正截面承载力计算中，应计入轴向压力在偏心方向存在的附加偏心距a e ，其值应取20mm 和偏心方向截面尺寸的1/30两者中的较大值。
引进附加偏心距后，在计算偏心受压构件正截面承载力时，应将轴向力作用点到截面形心的偏心距取为i e ，称为初始偏心距。
0i a e e e =+ （7-1）（五）偏心受压构件的二阶效应二阶效应——轴力在结构变形和位移时产生的附加内力。
图7-5 构件的二阶效应﹡在有侧移框架中，二阶效应主要是指竖向荷载在产生了侧移的框架中引起的附加内力，即通常称为P -∆效应。
﹡在无侧移框架中，二阶效应主要是指轴向力在产生了挠曲变形的柱段中引起的附加内力，通常称为P δ-效应。
(1) 偏心距增大法 2012011()1400i l e h hηζζ=+ （7-2） 10.5c f A Nζ=（7-2a ） 02 1.150.01l hζ=- （7-2b ） 式中 i e ——初始偏心距；0l ——构件的计算长度；h ——截面高度；其中，对环形截面，取外直径；对圆形截面，取直径；0h ——截面的有效高度；1ζ——偏心受压构件截面曲率修正系数；当0.11>ζ时，取0.11=ζ；2ζ——构件长细比对截面曲率的影响系数；当 015l h<时，取0.12=ζ； A ——构件截面面积；矩形截面h b A ⨯=；对于T 形和工字形 截面，均取'f 'f h b b bh A )(2-+=；N ——轴向压力设计值。
图7-6﹡当偏心受压构件的长细比l 0/i ≤17.5（对应的矩形截面为l 0/h ≤5）时，可取h =1.0；当l 0/i >17.5时，要按上式计算。
(2)刚度折减的弹性分析法采用有限元程序进行结构弹性分析，分析过程中应将构件刚度折减： 梁 为0.4 ；柱为0.6 ；剪力墙、核心筒壁为0.6。
按这样求得的内力可直接用于截面设计，e i 不需要再乘h 系数。
二、偏心受压构件正截面承载力计算（一）矩形截面非对称配筋构件正截面承载力1、基本计算公式及适用条件：(1)大偏压（0b h ξξ≤）：0X =∑，''1c y s y s N f bx f A f A α=+-（7-3） 0M =∑，'''100()()2c y s s x Ne f bx h f A h a α=-+-（7-4）2i s he e a η=+-（7-5）注意式中各符号的含义。
公式的适用条件：'2s x a ≥（7-6）0b h ξξ≤ （7-7） 界限情况下的b N ：''10b c b y s y s N f bh f A f A αξ=+-（7-8）当截面尺寸、配筋面积和材料强度为已知时，b N 为定值，按式（7-8）确定。
(2)小偏压（0b h ξξ>）：''1c s s y s N f bx f A A ασ=+- （7-9） '''1c 00()()2y s s x Ne f bx h f A h a α=-+- （7-10） 式中s σ根据实测结果可近似按下式计算： ''11y s yy b f f f ξβσξβ--≤=≤- （7-11）注意：﹡基本公式中'2s x a ≥条件满足时，才能保证受压钢筋达到屈服。
当'2s x a <时，受压钢筋达不到屈服，其正截面的承载力按下式计算。
y s 0s()Ne f A h a ''≤- （7-12）'e 为轴向压力作用点到受压纵向钢筋合力点的距离，计算中应计入偏心距增大系数。
﹡﹡矩形截面非对称配筋的小偏心受压构件，当N >f c bh 时，尚应按下列公式验算： )()21('0'01's 's 'y c a h A f h h bh f Ne -+-≤α （7-13） )(2a 0s e e a h e --'-=' （7-14） 式中，e '——轴向压力作用点到受压区纵向钢筋合力点的距离；h '——纵向受压钢筋合力点到截面远边的距离； 2、垂直于弯矩作用平面的受压承载力验算当轴向压力设计值N 较大且弯矩作用平面内的偏心距较小时，若垂直于弯矩作用平面的长细比较大或边长较小时，则有可能由垂直于弯矩作用平面的轴心受压承载力起控制作用。
因此，《规范》规定：偏心受压构件除应计算弯矩作用平面的受压承载力外，尚应按轴心受压构件验算垂直于弯矩作用平面的受压承载力，此时，可不计入弯矩的作用，但应考虑稳定系数的φ影响。
])[(9.0''c y s s Af f A A N ++≤ϕ（7-15） 3、公式的应用——矩形截面非对称配筋的计算方法计算可分为截面选择（设计题）和承载力验算（复核题）两类。
（1）截面选择（设计题）截面设计一般指配筋计算。
在A s 及's A 在未确定以前，ξ值是无法直接计算出来的。
因此就无法用ξ和ξb 做比较来判别是大偏压还是小偏压。
根据常用的材料强度及统计资料可知：在一般情况下，当ηe i >0.3h 0时，可按大偏压情况计算A s 及's A ；当ηe i ≤0.3h 0时，可按小偏压情况计算A s 及's A ；同时，在所有情况下，A s 及's A 还要满足最小配筋的规定；同时（A s +'s A ）不宜大于0.05bh 0。
1）大偏心受压（ηe i >0.3h 0）情况1：A s 及's A 均未知；可利用基本公式(7-3)，(7-4)计算，但有三个未知数A s 、's A 和 ξ，即要补充一个条件才能得到唯一解。
通常以A s +'s A 的总用量为最小作为补充条件，就应该充分发挥受压混凝土的作用并保证受拉钢筋屈服，此时，可取ξ=ξb 。
情况2：已知's A 求A s此时，可直接利用基本公式(7-3)，(7-4)求得唯一解，其计算过程与双筋矩形截面受弯构件类似，在计算中应注意验算适用条件。
举例：p197 例7-1。
2）小偏心受压（ηe i < 0.3h 0）情况1：A s 及's A 均未知由基本公式（7-9），（7-10）及式（7-11）可看出，未知数总共有四个A s 、's A 、σs 和 ξ，因此要得出唯一解，需要补充一个条件。
与大偏压的截面设计相仿，在A s 及's A 均未知时，以A s +'s A 为最小作为补充条件。
而在小偏压时，由于远离纵向力一侧的纵向钢筋不管是受拉还是受压均达不到屈服强度（除非是偏距心距过小，且轴向力很大），因此，一般可取A s 为按最小配筋百分率计算出钢筋的截面面积，这样得出的总用钢量为最少。
故取：bh A s min ρ=。
这样解联立方程就可求出'sA 。
情况2：已知A s 求's A ，或已知's A 求A s这种情况的未知数与可用的基本公式一致，可直接求出ξ和Ａs 或's A 。
