偏心受力构件
- 格式:doc
- 大小:601.00 KB
- 文档页数:9

第七章偏心受力构件一、选择题1.偏心受压构件计算中,通过哪个因素来考虑二阶偏心矩的影响( )。
A.e ; B.ae ; C.i e; D.η;2.判别大偏心受压破坏的本质条件是:( )。
A .03.0h e i >η;B .03.0h e i <η;C .B ξξ<;D .B ξξ>;3.由uu M N -相关曲线可以看出,下面观点不正确的是:( )。
A .小偏心受压情况下,随着N 的增加,正截面受弯承载力随之减小;B .大偏心受压情况下,随着N 的增加,正截面受弯承载力随之减小;C .界限破坏时,正截面受弯承载力达到最大值;D .对称配筋时,如果截面尺寸和形状相同,混凝土强度等级和钢筋级别也相同,但配筋数量不同,则在界限破坏时,它们的uN 是相同的;4.钢筋混凝土大偏压构件的破坏特征是:( )。
A.远侧钢筋受拉屈服,随后近侧钢筋受压屈服,混凝土也压碎;B.近侧钢筋受拉屈服,随后远侧钢筋受压屈服,混凝土也压碎;C.近侧钢筋和混凝土应力不定,远侧钢筋受拉屈服;D.远侧钢筋和混凝土应力不定,近侧钢筋受拉屈服;5.一对称配筋的大偏心受压构件,承受的四组内力中,最不利的一组内力为:( )。
A .m kN M ⋅=500 kN N 200=;B .m kN M ⋅=491 kN N 304=;C .m kN M ⋅=503 kN N 398=;D .m kN M ⋅-=512 kN N 506=; 6.一对称配筋的小偏心受压构件,承受的四组内力中,最不利的一组内力为:( )。
A .m kN M ⋅=525 kN N 2050=;B .m kN M ⋅=520 kN N 3060=;C .m kN M ⋅=524 kN N 3040=;D .m kN M ⋅=525 kN N 3090=; 7.偏压构件的抗弯承载力( )。
A.随着轴向力的增加而增加;B.随着轴向力的减少而增加;C.小偏压时随着轴向力的增加而增加;D.大偏压时随着轴向力的增加而增加;8.钢筋混凝土偏心受拉构件,判别大、小偏心受拉的根据是( )。




第七章 偏心受力构件承载力的计算西安交通大学土木工程系 杨 政第七章 偏心受力构件承载力的计算结构构件的截面受到轴力N和弯矩M共同作用,只在截 面上产生正应力,可以等效为一个偏心(偏心距 e0=M/N ) 作用的轴力N。
因此,截面上受到轴力和弯矩共同作用的结 构构件称为偏心受力构件。
N NM N(a )N N M(b )N(c )(d )(e )(f)第七章 偏心受力构件承载力的计算显然,轴心受力( e0=0 )和受弯( e0=∞)构件为其特 例。
当轴向力为压力时,称为偏心受压;当轴向力为拉力 时,称为偏心受拉。
偏心受压构件多采用矩形截面,工业建筑中尺寸较大的 预制柱也采用工字形和箱形截面,桥墩、桩及公共建筑中的 柱等多采用圆形截面;而偏心受拉构件多采用矩形截面。
e0=0 轴心受拉 偏心受拉 大偏心 e0=∞ 纯弯 偏心受压 小偏心 e0=0 轴心受压小偏心大偏心第七章 偏心受力构件承载力的计算7.1 偏心受压构件正截面承载力计算7.1.1 偏心受压构件的破坏形态偏心受压构件是工程中使用量最大 的结构构件,其受力性能随偏心距、配 筋率和长细比( l0/h )等主要因素而变 化。
与轴心受压构件类似,根据构件的 长细比,偏心受压柱也有长柱和短柱之 分。
此外,其他一些重要因素,例如混 凝土和钢筋材料的种类和强度等级、构 件的截面形状、钢筋的构造、荷载的施 加途径等,都对构件的受力性能和破坏 形态产生影响。
第七章 偏心受力构件承载力的计算受压(小偏心受压)破坏 偏心受压构件破坏类型 受拉(大偏心受压)破坏7.1 偏心受压构件正截面承载力计算第七章 偏心受力构件承载力的计算受压(小偏心受压)破坏 受压应力较大一侧的应变首先达到混凝土的极限压应变 而破坏,同侧的纵向钢筋也受压屈服;而另一侧纵向钢筋可 能受压也可能受拉,如果受压可能达到受压屈服,但如果受 拉,则不可能达到受拉屈服。
构件的承载力主要取决于受压混凝土和受压纵向钢筋。




即分为偏⼼受拉和偏⼼受压构件。
1.偏⼼受拉构件
(1)定义:构件承受的拉⼒作⽤点与构件的轴⼼偏离,使构件既受拉⼜受弯时,即为
偏⼼受拉构件(亦称拉弯构件)。
常见于屋架下弦有节间荷载时。
(2)构件的受⼒状态。
截⾯产⽣的应⼒是由两种应⼒叠加的,其边沿应⼒公式为:
= = = ( )
构件的承载能⼒应满⾜σmax≤[σ]
式中σmax——边沿拉应⼒;
σmin——边沿最⼩拉应⼒;
W——截⾯抵抗矩。
由上式可见,在受同样的外拉⼒时,偏⼼受拉构件,其应⼒耍⽐轴⼼受拉构件增⼤许多,因此在结构设计中应尽量避免出现这种构件。
2.偏⼼受压构件
(1)定义:构件承受的压⼒作⽤点与构件的轴⼼偏离,使构件既受压⼜受弯时即为偏⼼受压构件(亦称压弯构件)。
常见于屋架的上弦杆、框架结构柱、砖墙及砖垛等。
(2)构件的受⼒状态
截⾯产⽣的边沿应⼒公式为:
= == ( )
式中σmax⼀——边沿压应⼒;
σmin——边沿最⼩压应⼒。
由上式可见,在受同样的压⼒F时,当作⽤点与截⾯轴⼼偏离时,截⾯内的压应⼒增加甚多,⽽且当偏⼼距较⼤时截⾯内除压应⼒外将产⽣⼀部分拉应⼒。
在实践中尚有双向偏⼼构件。
偏心受压构件概念偏心受压构件是工程中常见的结构形式之一,由于其具有承受压力的能力,因此在建筑、桥梁、机械等领域得到广泛应用。
本文将从偏心距、偏心受力构件、弯矩、剪力、挠度、稳定性、极限承载力和失效等方面,介绍偏心受压构件的基本概念。
1.偏心距偏心距是指压力作用线与构件中心线的垂直距离。
在偏心受压构件中,压力作用线的位置是关键因素,它决定了构件的受力状态。
偏心距越大,压力作用线与构件中心线的偏离程度越大,构件承受的弯矩和剪力等内力也越大。
2.偏心受力构件偏心受力构件是指承受压力作用,且压力作用线与构件中心线不重合的构件。
这类构件在垂直于压力作用线的方向上会产生弯曲变形,导致构件内部产生弯矩和剪力等内力。
根据偏心程度的不同,偏心受力构件可以分为对称和非对称两种类型。
3.弯矩弯矩是指由于压力作用引起的截面弯曲变形所产生的力矩。
在偏心受压构件中,弯矩是导致构件破坏的主要因素之一。
弯矩的大小与压力大小、压力作用线的位置以及截面的形状和尺寸等因素有关。
4.剪力剪力是指由于压力作用引起的截面平行方向上的力。
在偏心受压构件中,剪力也是导致构件破坏的主要因素之一。
剪力的大小与压力作用线的位置、截面的形状和尺寸等因素有关。
5.挠度挠度是指偏心受压构件在压力作用下产生的弯曲变形程度。
挠度的大小直接反映了构件的弯曲程度,它的大小与压力大小、压力作用线的位置、截面的形状和尺寸等因素有关。
过大的挠度会导致构件失稳或破坏。
6.稳定性稳定性是指偏心受压构件在承受压力作用下保持其原有形状和平衡状态的能力。
在工程实际中,过大的挠度和剪力会导致构件失稳,从而引发安全事故。
因此,在设计和施工过程中需要采取措施提高构件的稳定性。
7.极限承载力极限承载力是指偏心受压构件在达到破坏极限时所能承受的最大压力。
在设计和施工过程中,需要根据规范和实际情况确定偏心受压构件的极限承载力,以确保构件在使用寿命内能够安全地承受预期的压力。
8.失效失效是指偏心受压构件在承受压力作用下失去其原有功能或完全破坏的现象。
第六章偏心受力构件
§6.1 偏心受力构件的特点及截面形式
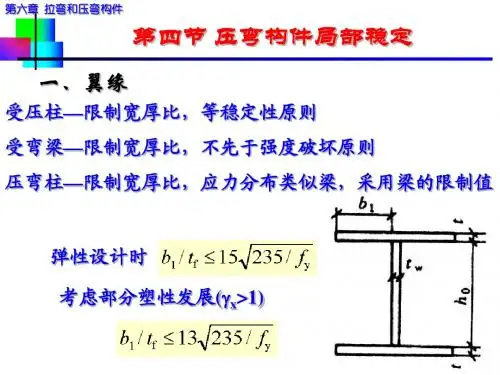
从偏心受力构件的特点来看,边缘很容易达到设计强度,若按边缘达塑性视
为强度极限很不经济,若按全截面达塑性,又会产生很大变形,因此与受弯构件相似,部分发展塑性。
(截面高度的4
8/1)
~
/1
§6.2 偏心受力构件的强度
ny
y y nx x x n W M W M A N
γγ±
±≤f y x ,M M ——两个主轴方向的弯矩
y x ,γγ——两个主轴方向的塑性发展因数,如工字形,x γ=1.05,y γ=1.20 需要计算疲劳的拉弯、压弯构件,宜取 1.0y x ==γγ
§6.3 实腹式偏心压杆的整体稳定
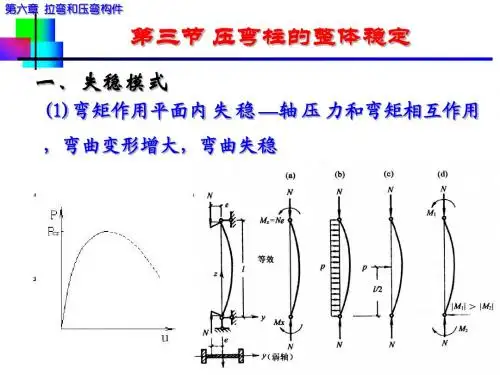
一.弯矩作用平面内的稳定
在弯矩作用平面内失稳属第二类稳定,偏心压杆的临界力与其相对偏心率
ρεe =有关,A W =ρ为截面核心矩,ρεe =大则临界力低。
通常采用的理论为压溃理论。
即:根据临界状态内外力平衡条件和变形调条件导出截面平均应力和杆中挠度的关系。
0),m cr =y σφ(
cr m
m cr 0)
,(σσφ−→−=dy y d
如此算得的平均应力值使变形过大,限制截面塑性发展在截面高度的
)4/1~8/1(,采用弹性相关公式加以修正。
1)
1(E s 0s
=-⋅++x
N N M e N M N N
0e ——偏心距
2x
2E πλEA
N x =
——欧拉临界力
1
x
1x y 1x s y s y I W f W M Af N =
==,, 1y ——受压最大点距中和轴距离
x
N N
E 1-
——弯矩放大因数(偏心矩增大因数) 考虑部分塑性发展,令p M 代替s M 则:
1)
1(E y 1x x 0s
=-⋅++x
N N
f W e N M N N γ
当M =0时,即为具有初始偏心0e 的轴心压杆,设其为x N (实际的轴心受力稳定承载力),则由上式可得:
A
W
N N N N N N e Ex x 1x x x x E x s 0))((γ⋅⋅--=
代回上式得:
1)
1(s
x
E y 1x x x
=⋅-+N N N N f W M
N N x γ
上式变为,,
x s
x
cr x ϕσ=⋅=N N A N
y E x 1x x x )
1(f N N
W M
A
N x
=-+ϕγϕ
由此式算得结果与实际有出入,经过修正:
)
0.81(E 1x x mx x x
N N
W M
A
N -⋅+γβϕ≤f
轴心受力构件中的考虑1000l 的初挠度,而偏压构件中的0e 很大,故此式误差就应主要在这里。
因为前面推导过程中的M 是按两端弯矩相等考虑的,mx β是考虑两端弯矩不等时的等效弯矩因数,其原则是二端弯矩不等时在杆中某一位置产生最大挠度,如两端弯矩相等,产生相同挠度,此弯矩为等效弯矩。
122
1m x ,
0.35
0.65M M M M >+=β
规范对mx β作出具体规定:
1. 弯矩作用平面同有侧移的框架柱悬臂构件mx β=1;
2. 无侧移框架柱和两端支承构件:
(1)没有横向荷载作用时,21m x /0.350.65M M +=β;
(2)有端弯矩和横向荷载同时作用,mx β=1;产生反向曲率mx β=0.85 (3)无端弯矩,有横向荷载:mx β=1
对于单轴对称截面,当弯矩使较大翼缘受压时,受拉区可能先受拉出现塑性:
)
1.251(Ex
2x x x
m x N N
W M A
N
-γβ-≤f
2x W ——受拉边截面抵抗矩,2
x
2x y I W =
2y ——受拉边缘到中和轴的距离
二.弯矩作用平面外的稳定
弯矩作用平面外稳定的机理与梁失稳的机理相同,因此其失稳形式也相同——平面外弯扭屈曲。
基本假定:
1.由于平面外截面刚度很大,故忽略该平面的挠曲变形。
2.杆件两端铰接,但不能绕纵轴转动。
3.材料为弹性。
tx x y b 1x
M N
A W βηϕϕ+≤f η——截面影响系数:闭口截面η=0.7,其他截面η=1.0;
y ϕ——弯矩作用平面外的稳定因数
b ϕ——均布弯矩作用下梁的整体稳定因数,工字形、T 形可按规范的简化方法计算;箱形截面b ϕ=1.0;
x M ——计算柱段内最大弯矩
tx β——等效弯矩因数(见规范有关规定)
以上计算结果是基于双轴对称工字形截面弹性工作范围得出的,对于单轴对称偏压构件以及弹塑性范围内,上述相关公式偏于安全。
对于不产生扭转的双轴对称截面(包括箱形截面),当弯矩作用在两个主平面时,公式可以推广验算稳定:
ty y mx x by 1y
x 1x
E (10.8)x x
M M N N A W W N ββηϕϕγ++⋅-≤f 及
my y tx x y bx 1x y 1y
E (10.8)y
M M N
N A W W N ββηϕκγ++
⋅-≤f
y x ,M M ——最大弯矩
ty tx my mx ,,,ββββ——等效弯矩因数,查规范。
by bx ,ϕϕ——受均布弯矩受弯构件对x,y 轴的整体稳定因数
§6.4 格构式偏心受压构件的整体稳定
对于宽度很大的偏心受压柱为了节省材料常采用格构式构件,且通常采用缀
一.偏心作用在虚轴上(绕实轴屈曲)
计算方法与实腹式柱偏心压杆相同,即: 平面内:
)
0.81(E 1y y my y y
N N
W M
A
N -⋅+γβϕ≤f
平面外:
1y
b y ty x W M A N
ϕβκ+
≤f
但是计算过程中,长细比应选用换算长细比0x λ(平面外)查x ϕ,b ϕ应取1.0。
二.偏心作用在实轴上(绕虚轴屈曲)
弯矩作用平面内:
)
(1E 1x mx x x
x N N
W M
A
N ϕβϕ-⋅+≤f
x ϕ——换算长细比对应的稳定因数
x N E ——换算长细比下的欧拉临界力 0
x
1x y I W =
0y ——受压肢中心到中和轴的距离
弯矩作用平面外:
因为平面外弯曲刚度大于平面内(实轴),故整体稳定不必验算,但要进行单肢的验算:
N a
e
y a e N a y N N ⋅+=⋅+⋅=
221 当两肢相同时,21y y =
验算单肢在1N 作用下绕1-1和y 轴的稳定。
平面内,10x l l =,0y l 取决于支撑情况,当不设支撑时,即为全高度。
y
0y y111
x1
i l i l =
=λλ, {}βϕλλ−→−y1x1,max 取
1
1
A N ⋅=
ϕσ≤f 当采用缀板柱时,单肢平面内除1N 外,还有局部弯矩,应按偏压实腹式构
件验算稳定。
缀件计算应采用实际剪力与计算剪力235
85
y m ax f f A V ⋅=
的较大值计算,当实
际剪力大于计算剪力时,宜采用实腹式构件(截面)。
三.双向偏心的格构式偏压构件
平面内:
1y
y
ty E x 1x x
mx x )
1(W M N N
W M A
N
x
βκβϕ+
-+≤f
平面外:(验算单肢):
⎪
⎪⎪⎩
⎪⎪
⎪⎨
⎧⋅⋅+=⋅+=+⋅+⋅=x
22
1111
y 1y 221y 2
1
e N y I y I y I M N a e y y y e N a y N N ⎪
⎪⎪⎩
⎪⎪
⎪⎨
⎧⋅⋅+=⋅-=+⋅-⋅=x
22
1122
y 2y 221y
12
e
N y I y I y I M N a e y y y e N a y N N 21,I I ——肢件1,2对y 轴的惯性矩,即将x M 分给单肢变为轴向力,再作用上y2y1,M M ,分别按偏心压杆验算整体(单肢)稳定。