非参数统计 随机游程检验

常用的非参数检验（NonparametricTests）总结非参数检验(Nonparametric tests)是统计分析方法的重要组成部分，它与参数检验共同构成统计推断的基本内容。

参数检验是在总体分布形式已知的情况下，对总体分布的参数如均值、方差等进行推断的方法。

但是，在数据分析过程中，由于种种原因，人们往往无法对总体分布形态作简单假定，此时参数检验的方法就不再适用了。

非参数检验正是一类基于这种考虑，在总体方差未知或知道甚少的情况下，利用样本数据对总体分布形态等进行推断的方法。

由于非参数检验方法在推断过程中不涉及有关总体分布的参数，因而得名为“非参数”检验。

•两独立样本的非参数检验两独立样本的非参数检验是在对总体分布不甚了解的情况下，通过对两组独立样本的分析来推断样本来自的两个总体的分布等是否存在显著差异的方法。

独立样本是指在一个总体中随机抽样对在另一个总体中随机抽样没有影响的情况下所获得的样本。

SPSS中提供了多种两独立样本的非参数检验方法，其中包括曼-惠特尼U检验、K-S检验、W-W游程检验、极端反应检验等。

某工厂用甲乙两种不同的工艺生产同一种产品。

如果希望检验两种工艺下产品的使用是否存在显著差异，可从两种工艺生产出的产品中随机抽样，得到各自的使用寿命数据。

甲工艺：675 682 692 679 669 661 693乙工艺：662 649 672 663 650 651 646 652（1）曼-惠特尼U检验两独立样本的曼-惠特尼U检验可用于对两总体分布的比例判断。

其原假设：两组独立样本来自的两总体分布无显著差异。

曼-惠特尼U 检验通过对两组样本平均秩的研究来实现判断。

秩简单说就是变量值排序的名次，可以将数据按升序排列，每个变量值都会有一个在整个变量值序列中的位置或名次，这个位置或名次就是变量值的秩。

（2）K-S检验K-S检验不仅能够检验单个总体是否服从某一理论分布，还能够检验两总体分布是否存在显著差异。

非参数检验介绍1 关于非参数的一些常识•经典统计的多数检验都假定了总体的背景分布。

•但在总体未知时，如果假定的总体和真实总体不符，那么就不适宜用通常的检验。

•这时如果利用传统的假定分布已知的检验，就会产生错误甚至灾难。

•无需假定总体分布的具体形式，仅仅依赖于数据观测值的相对大小(秩)或零假设下等可能的概率等和数据本身的具体总体分布无关的性质进行的检验都称为非参数检验(nonparametric testing)。

1 关于非参数的一些常识•这些非参数检验在总体分布未知时有很大的优越性。

它总是比传统检验安全。

•在总体分布形式已知时，非参数检验不如传统方法效率高。

这是因为非参数方法利用的信息要少些。

往往在传统方法可以拒绝零假设的情况，非参数检验无法拒绝。

•但非参数统计在总体未知时效率要比传统方法要高，有时要高很多。

是否用非参数统计方法，要根据对总体分布的了解程度来确定。

•这里介绍一些非参数检验。

•关于非参数方法的确切定义并不很明确。

我们就其最广泛的意义来理解。

•在计算中，诸如列联表分析中的许多问题都有精确方法，Monte Carlo 抽样方法和用于大样本的渐近方法等选择。

精确方法比较费时间，后两种要粗糙一些，但要快些。

秩（rank ）•非参数检验中秩是最常使用的概念。

什么是一个数据的秩呢？一般来说，秩就是该数据按照升幂排列之后，每个观测值的位置。

例如我们有下面数据X i 159183178513719R i75918426310这下面一行（记为R i ）就是上面一行数据X i 的秩。

秩（rank ）•利用秩的大小进行推断就避免了不知道背景分布的困难。

这也是非参数检验的优点。

•多数非参数检验明显地或隐含地利用了秩的性质；但也有一些非参数方法没有涉及秩的性质。

2 单样本检验2.1单样本中位数(α-分位数)符号检验•我们知道某点为中位数(α-分位数)意味着一个数小于该点的概率应该为0.5(α).•因此，一个观测值小于该点（或与该点之差的符号为负号）的概率为0.5(α)。

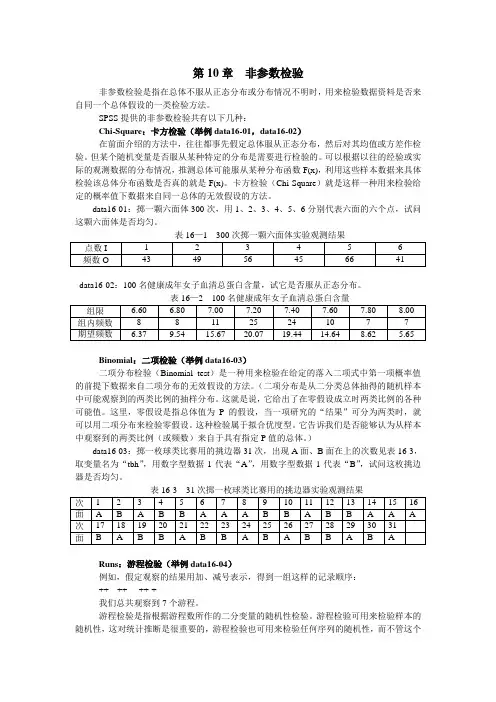
第10章非参数检验非参数检验是指在总体不服从正态分布或分布情况不明时，用来检验数据资料是否来自同一个总体假设的一类检验方法。

SPSS提供的非参数检验共有以下几种：Chi-Square：卡方检验（举例data16-01，data16-02）在前面介绍的方法中，往往都事先假定总体服从正态分布，然后对其均值或方差作检验。

但某个随机变量是否服从某种特定的分布是需要进行检验的。

可以根据以往的经验或实际的观测数据的分布情况，推测总体可能服从某种分布函数F(x)，利用这些样本数据来具体检验该总体分布函数是否真的就是F(x)。

卡方检验（Chi-Square）就是这样一种用来检验给定的概率值下数据来自同一总体的无效假设的方法。

data16-01：掷一颗六面体300次，用1、2、3、4、5、6分别代表六面的六个点，试问这颗六面体是否均匀。

表16—1 300次掷一颗六面体实验观测结果data16-02：100名健康成年女子血清总蛋白含量，试它是否服从正态分布。

Binomial：二项检验（举例data16-03）二项分布检验（Binomial test）是一种用来检验在给定的落入二项式中第一项概率值的前提下数据来自二项分布的无效假设的方法。

（二项分布是从二分类总体抽得的随机样本中可能观察到的两类比例的抽样分布。

这就是说，它给出了在零假设成立时两类比例的各种可能值。

这里，零假设是指总体值为P的假设，当一项研究的“结果”可分为两类时，就可以用二项分布来检验零假设。

这种检验属于拟合优度型。

它告诉我们是否能够认为从样本中观察到的两类比例（或频数）来自于具有指定P值的总体。

）data16-03：掷一枚球类比赛用的挑边器31次，出现A面、B面在上的次数见表16-3，取变量名为“tbh”，用数字型数据1代表“A”，用数字型数据1代表“B”，试问这枚挑边器是否均匀。

表16-3 31次掷一枚球类比赛用的挑边器实验观测结果Runs：游程检验（举例data16-04）例如，假定观察的结果用加、减号表示，得到一组这样的记录顺序：++---++----++-+我们总共观察到7个游程。

第十三章非参数统计分析统计推断方法大体上可分为两大类。

第一大类为参数统计方法。

常常在已知总体分布的条件下，对相应分布的总体参数进行估计和检验。

第二大类为非参数统计方法，着眼点不是总体参数，而是总体的分布情况或者样本所在总体分布的位置/形状。

非参数统计方法大约有8种，可被划分为两大类，处理各种不同情形的数据。

单样本情形：检验样本所在总体的位置参数或者分布是否与已知理论值相同。

①Chi-Square过程：针对二分类或者多分类资料例题1：见书P243。

检验样本分布情况是否与已知理论分布相同。

运用卡方检验过程。

②Binomial过程：针对二分类资料或者可转变为二分类问题的资料。

例题2 ：见书P246。

检验某一比例是否与已知比例相等，运用二项分布过程。

练习：质量监督部门对商店里面出售的某厂家的西洋参片进行了抽查。

对于25包写明为净重100g的西洋参片的称重结果为（单位：克），数据见非参数。

Sav，人们怀疑厂家包装的西洋参片份量不足，要求进行检验。

③Runs过程：用于检验样本序列是否是随机出现的。

二分类资料和连续性资料均可。

游程检验：游程的含义：假定下面是由0和1组成的一个这种变量的样本：0 0 0 0 1 1 1 1 1 1 0 0 1 0 1 1 1 0 0 0 0 0 0 0 0其中相同的0（或相同的1）在一起称为一个游程（单独的0或1也算）。

这个数据中有4个0组成的游程和3个1组成的游程。

一共是R=7个游程。

其中0的个数为m=15，而1的个数为n=10。

游程检验的原理判断数据序列是否是真随机序列。

该检验的原假设为数据是真随机序列，备择假设为非随机序列，在原假设成立的情况下，游程的总数不应太多也不应太少。

例题3：见书P247。

检验样本数据是否是随机出现的。

例题4：从某装瓶机出来的30盒化妆品的重量（单位克），数据见非参数.sav，为了看该装瓶机是否工作正常。

提示：实际需要验证大于和小于中位数的个数是否是随机的（零假设为这种个数的出现是随机的）。

非参数统计分析――Nonparametric Tests菜单详解非参数统计分析――Nonparametric Tests菜单详解平时我们使用的统计推断方法大多为参数统计方法，它们都是在已知总体分布的条件下，对相应分布的总体参数进行估计和检验。

比如单样本u检验就是假定该样本所在总体服从正态分布，然后推断总体的均数是否和已知的总体均数相同。

本节要讨论的统计方法着眼点不是总体参数，而是总体分布情况，即研究目标总体的分布是否与已知理论分布相同，或者各样本所在的分布位置/形状是否相同。

由于这一类方法不涉及总体参数，因而称为非参数统计方法。

SPSS的的Nonparametric Tests菜单中一共提供了8种非参数分析方法，它们可以被分为两大类：1、分布类型检验方法：亦称拟合优度检验方法。

即检验样本所在总体是否服从已知的理论分布。

具体包括：Chi-square test：用卡方检验来检验二项/多项分类变量的几个取值所占百分比是否和我们期望的比例有没有统计学差异。

Binomial Test：用于检测所给的变量是否符合二项分布，变量可以是两分类的，也可以使连续性变量，然后按你给出的分界点一分为二。

Runs Test：用于检验样本序列随机性。

观察某变量的取值是否是围绕着某个数值随机地上下波动，该数值可以是均数、中位数、众数或人为制定。

一般来说，如果该检验P值有统计学意义，则提示有其他变量对该变量的取值有影响，或该变量存在自相关。

One-Sample Kolmogorov-Smirnov Test：采用柯尔莫哥诺夫-斯米尔诺夫检验来分析变量是否符合某种分布，可以检验的分布有正态分布、均匀分布、Poission分布和指数分布。

2、分布位置检验方法：用于检验样本所在总体的分布位置/形状是否相同。

具体包括：Two-Independent-Samples Tests：即成组设计的两独立样本的秩和检验。

Tests for Several Independent Samples：成组设计的多个独立样本的秩和检验，此处不提供两两比较方法。

非参数统计分析方法一单样本问题1，二项式检验：检验样本参数是否与整体参数有什么关系。

样本量为n，给定一个实数M0（代表题目给出的分位点数），和分位点∏（0.25,0.5,0.75）。

用S-记做样本中比M0小的数的个数，S+记做样本中比M0大的数的个数。

如果原假设H0成立那么S-与n的比之应为∏。

H0：M=M0H1：M≠MO或者M>M0或者M<M0.Spss步骤：分析—非参数检验—二项式检验。

可以得出统计量为K=min（S-,S+）和统计量Z和p值当p值小于0.05时拒绝原假设，没有充足理由证明M=M0.,2，Wilcoxon符号秩序检验Wilcoxon检验的目的和二项式检验是一样的，Spss步骤：分析—非参数检验—两个相关样本得出统计量Z和p值当p值小于0.05时拒绝原假设，没有充足理由证明M=M03，随机性游程检验给出一组数据看次数据出现的情况是不是随机的。

列如：00011011110001110100001110H0：是随机的H1：不是随机的（混合倾向，游程多，长度短）（成群倾向，游程少，长度长）Spss步骤：分析—非参数检验—游程得出统计量R和p值当p值小于0.05时拒绝原假设，没有充足理由证明该数据出现是随机的二，两个样本位置问题1，Brown—Mood中位数检验给出两个样本比较两个样本的中位数或者四分位数等是否相等或者有一定关系，设一个中值为M1，一个为M2H0：M1=M2.H1：M1≠M2或者M1>M2或者M1<M2Spss步骤：分析—非参数检验—k个独立样本得出统计量Z和p值当p值小于0.05时拒绝原假设，没有充足理由证明M1=M2.2，Wilcoxon(Mann—Whitniey)秩和检验该检验和Brown—Mood检验的原理是一样的，但是该检验利用了更多的样本信息，从而比Brown—Mood检验更有说服力。

Spss步骤：分析—非参数检验—2个独立样本得到Z统计量和p值，当p值小于0.05时拒绝原假设，没有充足理由证明M1=M2.3，成对样本Wilcoxon秩和检验用M1代表开始时的数据某一特征值，用M2代表结束后的数据某一特征值，比较前后关系。

参数、非参数检验操作步骤参数检验非参数检验对象针对参数做的假设针对总体分布情况做的假设使用范围等距数据和比例数据（度量）定类数据和定序数据（名义和有序）分布正态分布正态、非正态分布内容Means检验单样本T检验独立样本T检验配对样本T检验卡方检验（均匀分布）二项分布检验（两个变量）游程检验（随机分布）K-S检验（正态分布检验）参数检验一Means过程Means过程用于统计分组变量的的基本统计量，这些基本统计量包括：均值（Mean）、标准差(Standard Deviation)、观察量数目(Number of Cases)、方差(Variance)。

1数据编辑窗口输入分析的数据2 分析→比较均值→均值因变量、自变量的选择可根据实际情况。

“选项”3 结果分析P＜0.05，拒绝原假设，显著性强。

结果报告，分别给出暴雨前和暴雨后卵量的统计量：暴雨前有13个样本，平均数122.3846，标准差15.95065，方差254.423; 暴雨后有13个样本，平均数104.4615，标准差15.10858，方差228.269；总体26个样本，平均数113.4231，标准差17.75426，方差315.214。

方差分析表，共有六列，第一列说明方差的来源，Between Groups是组间的，Within Groups 组内的，Total 总的。

第二列为平方和，其大小说明了各方差来源作用的大小。

第三列为自由度。

第四列为均方，即平方和除以自由度。

第五列F值是F统计量的值，其计算公式为模型均方除以误差均方，用来检验模型的显著性。

第六列是F统计量的显著值，由于这里的显著值0.007小于0.05，所以模型是显著的，降雨对卵量有显著影响。

二单一样本的T检验T检验是检验单个变量的均值与指定的检验值之间是否存在显著差异。

如：研究人员可能想知道一组学生的IQ平均分与100分的差异。

1 分析→比较均值→单一样本的T检验检验值中输入用于比较的均值（一般题目中会提供）。

第二讲 非参数检验1.实验目的1.了解非参数假设检验基本思想；2.会用SAS 软件中的proc npar1way 过程进行非参数假设检验和proc freq 过程进行列联表的独立性检验。

2.实验要求1.会用SAS 软件建立数据集, 并进行统计分析；2.掌握proc npar1way 过程进行非参数假设检验的基本步骤；3.掌握proc freq 过程进行列联表的独立性检验的基本步骤。

3.实验基本原理3.1 符号检验0:H 两种方法的处理效果无显著性差异令10i i I i ⎧=⎨⎩第个个体中新方法优于对照方法第个个体中新方法劣于对照方法1,2,,i N = 统计量1NN i i S I ==∑表示新方法的处理效果优于对照方法的配对组总数。

若新方法的处理效果显著的优于对照方法, 则 的值应明显偏大。

因此, 若对给定的置信水平 , 有 , 则拒绝 。

为真时, （1） 服从二项分布 。

拒绝域为:（2）由中心极限定理可知, 当 的零分布趋于标准正态分布。

拒绝域为：3.2 Wilcoxon 秩和检验（1）单边假设检验两种方法的处理效果无显著性差异 as : 新方法优于对照方法。

用于检验 的统计量为:若对给定的置信水平 , 有 , 则拒绝 。

且 的分布列为：0#{;,}{}H s w n m P W w N n ==⎛⎫ ⎪⎝⎭根据观测结果计算 的观测值 , 计算检验的p 值:00{}{}s H s s H s k w p P W w P W k ≥=≥==∑ 然后将 值与显著水平 作比较, 若 , 则拒绝 , 否则接受 。

（2）双边假设检验给定的显著水平 应该满足:ε=≥+≤}{}{2100c W P c W P A H A H 仅由上式还不能唯一确定 , 当我们对两种方法谁优谁劣不得而知时, 通常取 2}{}{2100α=≥=≤c W P c W P A H A H 若利用p 值进行检验, 设 ,计算概率值}{}{00A A H A A H W P W P ωω≤≥或由对称性可知, 检验的p 值为上述两概率中小于1/2的那一个的2倍。

非参数统计随机游程检验非参数统计学是一种不需要假设总体分布函数形式的统计方法。

它主要侧重于使用统计量对样本进行推断和推断总体特征。

在非参数统计学中，我们使用有关样本的排序信息来进行统计推断，而不是使用参数模型的参数。

非参数统计学方法的一个重要应用是迫使数据适应理论上更普遍的概率分布，而不是仅局限于已知参数模型的特定假设。

随机游程检验（RST）是非参数统计学的一种方法，用于检验是否存在随机性或随机分布。

随机游程检验的基本思想是将样本中的值分为两种可能的状态（通常为两个水平），然后检验这两种状态是否以随机的方式交替出现。

如果交替出现的状态被证明是非随机的，则可以得出结论样本中存在一种模式或趋势。

随机游程检验具体有两种常见的形式：游程上涨和游程下降。

游程上涨是指在两个状态之间有连续递增的游程，而游程下降则是指在两个状态之间有连续递减的游程。

在随机性的假设下，我们可以推断游程长度的分布。

如果观测到的游程长度远远大于或小于预期的值，则可以推断存在非随机趋势或模式。

随机游程检验的一个常见应用是检验序列是否是随机生成的。

例如，在密码学中，随机性对于生成安全的密码是至关重要的。

通过对密码序列进行随机游程检验，我们可以检验它是否是伪随机的，即不容易由其他人猜测。

随机游程检验还可以用于分析一系列事件的随机性，例如金融时间序列、环境数据、医学数据等。

总结起来，随机游程检验是非参数统计学中的一种方法，用于检验样本序列中是否存在随机性或趋势。

通过将样本序列分为相邻的游程，并计算游程的长度，我们可以推断是否存在非随机模式。

随机游程检验在多个领域中有广泛的应用，如密码学、金融、环境和医学研究等。