异方差检验的eviews操作
- 格式:docx
- 大小:37.68 KB
- 文档页数:9

eviews异方差检验步骤Eviews是一款常用的经济学软件,它允许用户进行多种统计分析,其中包括异方差检验。
异方差是指随着自变量的变化,因变量的方差也会发生变化。
在实际分析中,如果忽略了异方差,则会导致统计结果不准确。
因此,在使用Eviews进行分析时,进行异方差检验十分重要。
以下是Eviews进行异方差检验的步骤:1. 打开Eviews软件,并导入所需的数据。
在“工作文件”菜单下选择“打开文件”,找到所需的数据文件并打开。
2. 选择变量。
单击“变量”菜单,并选择要检验的因变量和自变量。
如果有多个自变量,在本例中就需要选择多个自变量。
3. 进行回归分析。
单击“Quick”菜单下的“Estimate Equation”选项,进行回归分析。
在回归分析中,需要输入因变量和自变量,并进行模型估计。
4. 异方差检验。
在回归分析完成后,单击“View”菜单下的“Residual Diagnostics”选项,进入错误项诊断。
5. 在错误项诊断中选择异方差检验。
在错误项诊断面板中,选择“Heteroskedasticity Tests”选项,并选择所需的异方差检验类型。
在Eviews中,通常可以使用Breusch-Pagan/Godfrey测试或White 测试来检验异方差。
6. 查看结果。
完成异方差检验后,Eviews会返回检验结果。
如果结果显示存在异方差,则需要进行调整,以消除异方差的影响。
总之,在使用Eviews进行经济学分析时,进行异方差检验至关重要,可以保证模型分析的准确性和可靠性。
上述步骤简单易懂,只要按照步骤操作,就可以轻松地完成异方差检验。
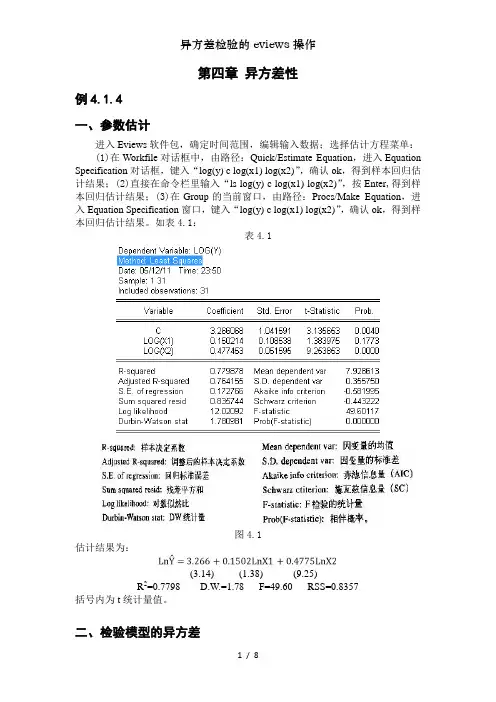
第四章异方差性例4.1.4一、参数估计进入Eviews软件包,确定时间范围,编辑输入数据;选择估计方程菜单:(1)在Workfile对话框中,由路径:Quick/Estimate Equation,进入Equation Specification对话框,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果;(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”,按Enter,得到样本回归估计结果;(3)在Group的当前窗口,由路径:Procs/Make Equation,进入Equation Specification窗口,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果。
如表4.1:表4.1图4.1估计结果为:(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。
二、检验模型的异方差(一)图形法(1)生成残差平方序列。
①在Workfile的对话框中,由路径:Procs/Generate Series,进入Generate Series by Equation对话框,键入“e2=resid^2”,生成残差平方项序列e2;②直接在命令栏里输入“genr e2=resid^2”,按Enter,得到残差平方项序列e2。
(2)绘制散点图。
①直接在命令框里输入“scat log(x2) e2”,按Enter,可得散点图4.2。
②选择变量名log(x2)与e2(注意选择变量的顺序,先选的变量将在图形中表示横轴,后选的变量表示纵轴),再按路径view/graph/scatter/simple scatter,可得散点图4.2。
③由路径quick/graph进入series list窗口,输入“log(x2) e2”,确认并ok,再在弹出的graph窗口把line graph换成scatter diagram,再点ok,可得散点图4.2。


第四章异方差性例4.1.4一、参数估计进入Eviews软件包,确定时间范围,编辑输入数据;选择估计方程菜单:(1)在Workfile对话框中,由路径:Quick/Estimate Equation,进入Equation Specification对话框,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果;(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”,按Enter,得到样本回归估计结果;(3)在Group的当前窗口,由路径:Procs/Make Equation,进入Equation Specification窗口,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果。
如表4.1:表4.1图4.1估计结果为:(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。
二、检验模型的异方差(一)图形法(1)生成残差平方序列。
①在Workfile的对话框中,由路径:Procs/Generate Series,进入Generate Series by Equation 对话框,键入“e2=resid^2”,生成残差平方项序列e2;②直接在命令栏里输入“genr e2=resid^2”,按Enter,得到残差平方项序列e2。
(2)绘制散点图。
①直接在命令框里输入“scat log(x2) e2”,按Enter,可得散点图4.2。
②选择变量名log(x2)与e2(注意选择变量的顺序,先选的变量将在图形中表示横轴,后选的变量表示纵轴),再按路径view/graph/scatter/simple scatter,可得散点图4.2。
③由路径quick/graph进入series list窗口,输入“log(x2) e2”,确认并ok,再在弹出的graph窗口把line graph换成scatter diagram,再点ok,可得散点图4.2。

异方差的eviews操作图3-1 我国制造工业销售利润与销售收入相关图从图中可以看出,随着销售收入的增加,销售利润的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
⑵残差分析首先将数据排序(命令格式为:SORT 解释变量),然后建立回归方程。
在方程窗口中点击Resids按钮就可以得到模型的残差分布图(或建立方程后在Eviews工作文件窗口中点击resid对象来观察)。
图3-2 我国制造业销售利润回归模型残差分布图3-2显示回归方程的残差分布有明显的扩大趋势,即表明存在异方差性。
2、Goldfeld-Quant检验⑴将样本安解释变量排序(SORT X)并分成两部分(分别有1到10共11个样本合19到28共10个样本)⑵利用样本1建立回归模型1(回归结果如图3-3),其残差平方和为2579.587。
SMPL 1 10LS Y C X图3-3 样本1回归结果⑶利用样本2建立回归模型2(回归结果如图3-4),其残差平方和为63769.67。
SMPL 19 28 LS Y C X图3-4 样本2回归结果⑷计算F 统计量:12/RSS RSS F ==63769.67/2579.59=24.72,21RSS RSS 和分别是模型1和模型2的残差平方和。
取05.0=α时,查F 分布表得44.3)1110,1110(05.0=----F ,而44.372.2405.0=>=F F ,所以存在异方差性3、White 检验⑴建立回归模型:LS Y C X ,回归结果如图3-5。
图3-5 我国制造业销售利润回归模型⑵在方程窗口上点击View\Residual\Test\White Heteroskedastcity,检验结果如图3-6。
图3-6 White 检验结果其中F 值为辅助回归模型的F 统计量值。
取显著水平05.0=α,由于2704.699.5)2(2205.0=<=nR χ,所以存在异方差性。
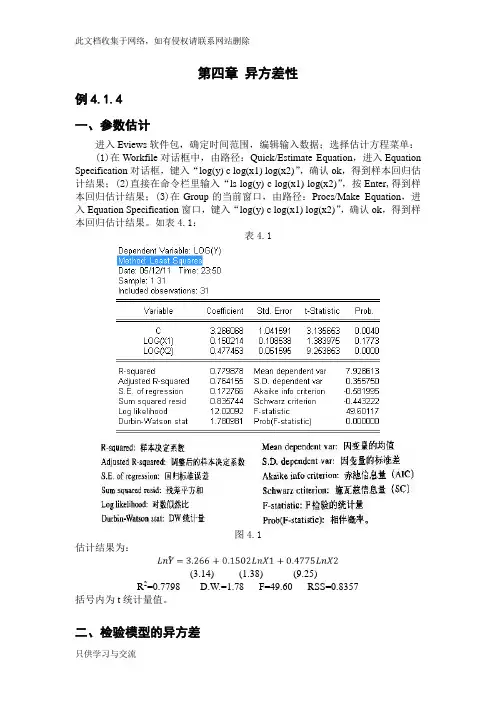
第四章异方差性例4.1.4一、参数估计进入Eviews软件包,确定时间范围,编辑输入数据;选择估计方程菜单:(1)在Workfile对话框中,由路径:Quick/Estimate Equation,进入Equation Specification对话框,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果;(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”,按Enter,得到样本回归估计结果;(3)在Group的当前窗口,由路径:Procs/Make Equation,进入Equation Specification窗口,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果。
如表4.1:表4.1图4.1估计结果为:(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。
二、检验模型的异方差(一)图形法(1)生成残差平方序列。
①在Workfile的对话框中,由路径:Procs/Generate Series,进入Generate Series by Equation对话框,键入“e2=resid^2”,生成残差平方项序列e2;②直接在命令栏里输入“genr e2=resid^2”,按Enter,得到残差平方项序列e2。
(2)绘制散点图。
①直接在命令框里输入“scat log(x2) e2”,按Enter,可得散点图4.2。
②选择变量名log(x2)与e2(注意选择变量的顺序,先选的变量将在图形中表示横轴,后选的变量表示纵轴),再按路径view/graph/scatter/simple scatter,可得散点图4.2。
③由路径quick/graph进入series list窗口,输入“log(x2) e2”,确认并ok,再在弹出的graph窗口把line graph换成scatter diagram,再点ok,可得散点图4.2。

第四章异方差性例4.1.4一、参数估计进入Eviews软件包,确定时间范围,编辑输入数据;选择估计方程菜单:(1)在Workfile对话框中,由路径:Quick/Estimate Equation,进入Equation Specification对话框,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果;(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”,按Enter,得到样本回归估计结果;(3)在Group的当前窗口,由路径:Procs/Make Equation,进入Equation Specification窗口,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果。
如表4.1:表4.1图4.1估计结果为:(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。
二、检验模型的异方差(一)图形法(1)生成残差平方序列。
①在Workfile的对话框中,由路径:Procs/Generate Series,进入Generate Series by Equation对话框,键入“e2=resid^2”,生成残差平方项序列e2;②直接在命令栏里输入“genr e2=resid^2”,按Enter,得到残差平方项序列e2。
(2)绘制散点图。
①直接在命令框里输入“scat log(x2) e2”,按Enter,可得散点图4.2。
②选择变量名log(x2)与e2(注意选择变量的顺序,先选的变量将在图形中表示横轴,后选的变量表示纵轴),再按路径view/graph/scatter/simple scatter ,可得散点图4.2。
③由路径quick/graph进入series list窗口,输入“log(x2) e2”,确认并ok,再在弹出的graph窗口把line graph换成scatter diagram,再点ok,可得散点图4.2。


实验三异方差的检验与修正实验目的1、理解异方差的含义后果、2、学会异方差的检验与加权最小二乘法实验内容一、准备工作。
建立工作文件,并输入数据,用普通最小二乘法估计方程(操作步骤与方法同前),得到残差序列。
表2列出了1998年我国主要制造工业销售收入与销售利润的统计资料,请利用统计软件Eviews建立我国制造业利润函数模型。
表2 我国制造工业1998年销售利润与销售收入情况二、异方差的检验1、图形分析检验⑴观察销售利润(Y)与销售收入(X)的相关图(图3-1):SCAT X Y图3-1 我国制造工业销售利润与销售收入相关图从图中可以看出,随着销售收入的增加,销售利润的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
⑵残差分析首先将数据排序(命令格式为:SORT 解释变量),然后建立回归方程。
在方程窗口中点击Resids按钮就可以得到模型的残差分布图(或建立方程后在Eviews工作文件窗口中点击resid对象来观察)。
图3-2 我国制造业销售利润回归模型残差分布图3-2显示回归方程的残差分布有明显的扩大趋势,即表明存在异方差性。
2、Goldfeld-Quant检验⑴将样本安解释变量排序(SORT X)并分成两部分(分别有1到10共11个样本合19到28共10个样本)⑵利用样本1建立回归模型1(回归结果如图3-3),其残差平方和为2579.587。
SMPL 1 10LS Y C X图3-3 样本1回归结果⑶利用样本2建立回归模型2(回归结果如图3-4),其残差平方和为63769.67。
SMPL 19 28 LS Y C X图3-4 样本2回归结果⑷计算F 统计量:12/RSS RSS F ==63769.67/2579.59=24.72,21RSS RSS 和分别是模型1和模型2的残差平方和。
取05.0=α时,查F 分布表得44.3)1110,1110(05.0=----F ,而44.372.2405.0=>=F F ,所以存在异方差性3、White 检验⑴建立回归模型:LS Y C X ,回归结果如图3-5。
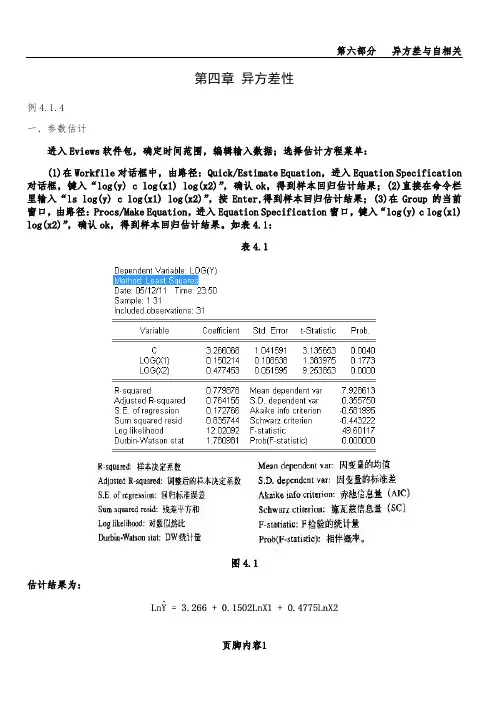
第四章异方差性例4.1.4一、参数估计进入Eviews软件包,确定时间范围,编辑输入数据;选择估计方程菜单:(1)在Workfile对话框中,由路径:Quick/Estimate Equation,进入Equation Specification 对话框,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果;(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”,按Enter,得到样本回归估计结果;(3)在Group的当前窗口,由路径:Procs/Make Equation,进入Equation Specification窗口,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果。
如表4.1:表4.1图4.1估计结果为:(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。
二、检验模型的异方差(一)图形法(1)生成残差平方序列。
①在Workfile的对话框中,由路径:Procs/Generate Series,进入Generate Series by Equation对话框,键入“e2=resid^2”,生成残差平方项序列e2;②直接在命令栏里输入“genr e2=resid^2”,按Enter,得到残差平方项序列e2。
(2)绘制散点图。
①直接在命令框里输入“scat log(x2) e2”,按Enter,可得散点图4.2。
②选择变量名log(x2)与e2(注意选择变量的顺序,先选的变量将在图形中表示横轴,后选的变量表示纵轴),再按路径view/graph/scatter/simple scatter ,可得散点图4.2。
③由路径quick/graph进入series list窗口,输入“log(x2) e2”,确认并ok,再在弹出的graph窗口把line graph换成scatter diagram,再点ok,可得散点图4.2。

第四章异方差性例4.1.4一、参数估计进入Eviews软件包,确定时间范围,编辑输入数据;选择估计方程菜单:(1)在Workfile对话框中,由路径:Quick/Estimate Equation,进入Equation Specification对话框,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果;(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”,按Enter,得到样本回归估计结果;(3)在Group的当前窗口,由路径:Procs/Make Equation,进入Equation Specification窗口,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果。
如表4.1:表4.1图4.1估计结果为:(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。
二、检验模型的异方差(一)图形法(1)生成残差平方序列。
①在Workfile的对话框中,由路径:Procs/Generate Series,进入Generate Series by Equation对话框,键入“e2=resid^2”,生成残差平方项序列e2;②直接在命令栏里输入“genr e2=resid^2”,按Enter,得到残差平方项序列e2。
(2)绘制散点图。
①直接在命令框里输入“scat log(x2) e2”,按Enter,可得散点图4.2。
②选择变量名log(x2)与e2(注意选择变量的顺序,先选的变量将在图形中表示横轴,后选的变量表示纵轴),再按路径view/graph/scatter/simple scatter,可得散点图4.2。
③由路径quick/graph进入series list窗口,输入“log(x2) e2”,确认并ok,再在弹出的graph窗口把line graph换成scatter diagram,再点ok,可得散点图4.2。
eviews异方差检验步骤Eviews异方差检验步骤异方差是指随着自变量的变化,因变量的方差也会发生变化。
在回归分析中,如果存在异方差,会导致回归系数的估计值不准确,从而影响模型的可靠性。
因此,进行异方差检验是非常重要的。
Eviews是一款常用的统计软件,它提供了多种方法来检验异方差。
下面我们将介绍Eviews中进行异方差检验的步骤。
步骤一:建立回归模型我们需要建立一个回归模型。
在Eviews中,可以通过“Quick”菜单中的“Estimate Equation”来建立回归模型。
在弹出的对话框中,选择因变量和自变量,并设置其他参数,如拟合方法、截距项等。
步骤二:检验异方差建立好回归模型后,我们需要进行异方差检验。
在Eviews中,可以通过“View”菜单中的“Residual Diagnostics”来进行检验。
在弹出的对话框中,选择“Heteroskedasticity Tests”选项卡,然后选择需要进行的异方差检验方法。
Eviews提供了多种异方差检验方法,包括Breusch-Pagan-Godfrey 检验、White检验、Goldfeld-Quandt检验等。
这些方法的原理和适用条件不同,需要根据具体情况选择合适的方法。
步骤三:解释检验结果进行异方差检验后,Eviews会输出检验结果。
通常包括检验统计量、p值等信息。
如果p值小于显著性水平(通常为0.05),则可以拒绝原假设,认为存在异方差。
如果检验结果显示存在异方差,我们需要对模型进行修正。
常用的方法包括使用异方差稳健标准误、进行加权最小二乘回归等。
总结Eviews提供了多种方法来检验异方差,包括Breusch-Pagan-Godfrey 检验、White检验、Goldfeld-Quandt检验等。
进行异方差检验后,需要根据检验结果对模型进行修正,以提高模型的可靠性。
eviews异方差、自相关检验与解决办法一、异方差检验:1.相关图检验法LS Y C X 对模型进行参数估计GENR E=RESID 求出残差序列GENR E2=E^2 求出残差的平方序列SORT X 对解释变量X排序SCAT X E2 画出残差平方与解释变量X的相关图2.戈德菲尔德——匡特检验已知样本容量n=26,去掉中间6个样本点(即约n/4),形成两个样本容量均为10的子样本。
SORT X 将样本数据关于X排序SMPL 1 10 确定子样本1LS Y C X 求出子样本1的回归平方和RSS1SMPL 17 26 确定子样本2LS Y C X 求出子样本2的回归平方和RSS2计算F统计量并做出判断。
解决办法3.加权最小二乘法LS Y C X 最小二乘法估计,得到残差序列GRNR E1=ABS(RESID) 生成残差绝对值序列LS(W=1/E1) Y C X 以E1为权数进行加权最小二成估计二、自相关1.图示法检验LS Y C X 最小二乘法估计,得到残差序列GENR E=RESID 生成残差序列SCAT E(-1) E et—et-1的散点图PLOT E 还可绘制et的趋势图2.广义差分法LS Y C X AR(1) AR(2)首先,你要对广义差分法熟悉,不是了解,如果你是外行,我奉劝你还是用eviews来做就行了,其实我想老师要你用spss无非是想看你是否掌握广义差分,好了,废话不多说了。
接着,使用spss16来解决自相关。
第一步,输入变量,做线性回归,注意在Liner Regression 中的Statistics中勾上DW,在save中勾Standardized,查看结果,显然肯定是有自相关的(看dw值)。
第二步,做滞后一期的残差,直接COPY数据(别告诉我不会啊),然后将残差和滞后一期的残差做回归,记下它们之间的B指(就是斜率)。
第三步,再做滞后一期的X1和Y1,即自变量和因变量的滞后一期的值,也是直接COPY。
第四章异方差性例4.1.4一、参数估计进入Eviews软件包,确定时间范围,编辑输入数据;选择估计方程菜单:(1)在Workfile对话框中,由路径:Quick/Estimate Equation,进入Equation Specification对话框,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果;(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”,按Enter,得到样本回归估计结果;(3)在Group的当前窗口,由路径:Procs/Make Equation,进入Equation Specification窗口,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果。
如表4.1:表4.1图4.1估计结果为:(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。
二、检验模型的异方差(一)图形法(1)生成残差平方序列。
①在Workfile的对话框中,由路径:Procs/Generate Series,进入Generate Series by Equation对话框,键入“e2=resid^2”,生成残差平方项序列e2;②直接在命令栏里输入“genr e2=resid^2”,按Enter,得到残差平方项序列e2。
(2)绘制散点图。
①直接在命令框里输入“scat log(x2) e2”,按Enter,可得散点图4.2。
②选择变量名log(x2)与e2(注意选择变量的顺序,先选的变量将在图形中表示横轴,后选的变量表示纵轴),再按路径view/graph/scatter/simple scatter,可得散点图4.2。
③由路径quick/graph进入series list窗口,输入“log(x2) e2”,确认并ok,再在弹出的graph窗口把line graph换成scatter diagram,再点ok,可得散点图4.2。
第四章异方差性例一、参数估计进入Eviews软件包,确定时间范围,编辑输入数据;选择估计方程菜单:(1)在Workfile对话框中,由路径:Quick/Estimate Equation,进入Equation Specification对话框,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果;(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”,按Enter,得到样本回归估计结果;(3)在Group的当前窗口,由路径:Procs/Make Equation,进入Equation Specification窗口,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果。
如表:表图估计结果为:R2= .= F= RSS=括号内为t统计量值。
二、检验模型的异方差(一)图形法(1)生成残差平方序列。
①在Workfile的对话框中,由路径:Procs/Generate Series,进入Generate Series by Equation对话框,键入“e2=resid^2”,生成残差平方项序列e2;②直接在命令栏里输入“genr e2=resid^2”,按Enter,得到残差平方项序列e2。
(2)绘制散点图。
①直接在命令框里输入“scat log(x2) e2”,按Enter,可得散点图。
②选择变量名log(x2)与e2(注意选择变量的顺序,先选的变量将在图形中表示横轴,后选的变量表示纵轴),再按路径view/graph/scatter/simple scatter ,可得散点图。
③由路径quick/graph进入series list窗口,输入“log(x2) e2”,确认并ok,再在弹出的graph窗口把line graph换成scatter diagram,再点ok,可得散点图。
图由图可以看出,残差平方项e2对解释变量log(X2)的散点图主要分布图形中的下三角部分,大致看出残差平方项e2随log(X2)的变动呈增大的趋势,因此,模型很可能存在异方差。
第四章异方差性例4.1.4一、参数估计进入Eviews软件包,确定时间范围,编辑输入数据;选择估计方程菜单:(1)在Workfile对话框中,由路径:Quick/Estimate Equation,进入Equation Specification对话框,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果;(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”,按Enter,得到样本回归估计结果;(3)在Group的当前窗口,由路径:Procs/Make Equation,进入Equation Specification窗口,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果。
如表4.1:表4.1图4.1估计结果为:LnŶ=3.266+0.1502LnX1+0.4775LnX2(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。
二、检验模型的异方差(一)图形法(1)生成残差平方序列。
①在Workfile的对话框中,由路径:Procs/Generate Series,进入Generate Series by Equation对话框,键入“e2=resid^2”,生成残差平方项序列e2;②直接在命令栏里输入“genr e2=resid^2”,按Enter,得到残差平方项序列e2。
(2)绘制散点图。
①直接在命令框里输入“scat log(x2) e2”,按Enter,可得散点图4.2。
②选择变量名log(x2)与e2(注意选择变量的顺序,先选的变量将在图形中表示横轴,后选的变量表示纵轴),再按路径view/graph/scatter/simple scatter,可得散点图4.2。
③由路径quick/graph进入series list窗口,输入“log(x2) e2”,确认并ok,再在弹出的graph窗口把line graph换成scatter diagram,再点ok,可得散点图4.2。
第四章异方差性例4.1.4一、参数估计进入Eviews软件包,确定时间围,编辑输入数据;选择估计方程菜单:(1)在Workfile对话框中,由路径:Quick/Estimate Equation,进入Equation Specification对话框,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果;(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”,按Enter,得到样本回归估计结果;(3)在Group的当前窗口,由路径:Procs/Make Equation,进入Equation Specification窗口,键入“log(y) c log(x1) log(x2)”,确认ok,得到样本回归估计结果。
如表4.1:表4.1图4.1估计结果为:(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号为t统计量值。
二、检验模型的异方差(一)图形法(1)生成残差平方序列。
①在Workfile的对话框中,由路径:Procs/Generate Series,进入Generate Series by Equation对话框,键入“e2=resid^2”,生成残差平方项序列e2;②直接在命令栏里输入“genr e2=resid^2”,按Enter,得到残差平方项序列e2。
(2)绘制散点图。
①直接在命令框里输入“scat log(x2) e2”,按Enter,可得散点图4.2。
②选择变量名log(x2)与e2(注意选择变量的顺序,先选的变量将在图形中表示横轴,后选的变量表示纵轴),再按路径view/graph/scatter/simple scatter ,可得散点图4.2。
③由路径quick/graph进入series list窗口,输入“log(x2) e2”,确认并ok,再在弹出的graph窗口把line graph换成scatter diagram,再点ok,可得散点图4.2。
第四章异方差性例 4.1.4 、参数估计进入Eviews 软件包,确定时间范围,编辑输入数据;选择估计方程菜单: (1)在 Workfile 对话框中,由路径:Quick/Estimate Equation ,进入 EquationSpecification 对话框,键入“ log(y) c Iog(x1) Iog(x2) ”,确认ok ,得到样本回归估 计结果;⑵ 直接在命令栏里输入“ ls log(y) c log(x1) Iog(x2) ”,按Enter,得到样 本回归估计结果;(3)在Group 的当前窗口,由路径:Procs/Make Equation ,进 入Equation Specification 窗口,键入“ log(y) c log(x1) log(x2) ”,确认 ok ,得到样 本回归估计结果。
如表4.1 :表4.1D 即的血nt y 計怕blr LOGpOiMethod; Least EquaresIDate: 05/12/11 Time- 23:50Sample: 1 31Included observat io ns: 31Variable Coefficient Stet Error t-Statistic Prob. C 3 266066 1.041591 3 135653 0.0040 LOG (XI)0.150214 0.103538 1.363975 0.1773 LOGpG)0.477i53 0 0515959 253053O.ODODR-squared0.779376 Mean de 卩end ent war 7.323613 Adjusted R-squared 0764155 S D. riependent var 0.355750 S. E. of regression 0.1727&E Aka ike info criterion -□.5S1995 Sum sq jarEd res id 0.335744 Schwa rz criteiriior -0.443222 Log likelihood 12.02092 F-statistic J9.60117 Durbin-Watson stat1.780931P rab(F-£taii&tic) □.aOODQD图4.1估计结果为: 一LiiY= 3-266+ 0L1502 LnXl + 0.4775 LuX2(3.14)(1.38)(9.25)R 2=O.7798D.W=1.78 F=49.6ORSS=O.8357括号内为t 统计量值。
Adjiisiei R-^quared;関望 ER 冲■Wt定爲數 S,E. of re^Rirtiun:回扫标准谡羞Sam squared reakl' S 差平方祁 Leg Likdibwxl:对数似協比Mean dependent var: ft 的均K10. depenjent var 因(1^标堆差info criteticn:赤池怙息ft (AJC)Seh^arz etiferitw: ®瓦茲信息量(SC) F-siatifitic: F 检轻的铳计量 Prob[h-stau>tk); ffi 伴fit 札精品文库二、检验模型的异方差(一) 图形法(1) 生成残差平方序列。
①在 Workfile 的对话框中,由路径:P rocs/Ge nerateSeries,进入 Gen erate② 选择变量名log(x2)与e2 (注意选择变量的顺序,先选的变量将在图形中 表示横轴,后选的变量表示纵轴),再按路径view/graph/scatter/simple scatter , 可得散点图4.2。
③由路径 quick/gra ph 进入 series list 窗口,输入“ Iog(x2) e2 ”,确认并 ok . 再在弹出的graph 窗口把line graph 换成scatter diagram,再点ok ,可得散点图 4.2。
0-25-10_£0-0J5- LUOJO-■30.00-_TS图4.2由图4.2可以看出,残差平方项e2对解释变量log(X2)的散点图主要分布图 形中的下三角部分,大致看出残差平方项e2随log(X2)的变动呈增大的趋势,因 此,模型很可能存在异方差。
但是否确实存在异方差还应通过更进一步的检验。
(二) Goldfeld-Quanadt 检验(1)对变量取值排序(按递增或递减)。
①在 Workfile 窗口中,由路径:Procs/Sort Series 进入 sort workfile series 对 话框,键入“ X2 ”,如果以递增型排序,选 Ascen di ng,如果以递减型排序,贝U 应选Descending,点ok 。
本例选递增型排序,选 Ascending 。
Series by Equation 对话框,键入“ e2=resid^2'',生成残差平方项序列 接在命令栏里输入“ genr e2=resid 吃,按Enter,得到残差平方项序列(2)绘制散点图。
① 直接在命令框里输入“ scat log(x2) e2',按Enter ,可得散点图e2;②直e2。
4.2。
口 Q rtTiCl②直接在命令栏里输入“ sort x2”(默认为升序),再按Enter o(2)构造子样本区间,建立回归模型。
在本例中,样本容量n=31,删除中间1/4的观测值,即大约7个观测值,余下部分平分得两个样本区间:1-12和20-31,它们的样本个数均是12个。
在Sample菜单里,把sampie值改为“1 12”再用OLS方法进行第一个子样本回归估计,估计结果如表4.2 0表4.2Dependent V^riablle' L0G(V) Method: Lea si Squares Date: 05/13/11 Time: 03:00Sample: 1 12Included observations: 12匚Variable CoeJTiStd. Error b Statistic Prob.i&ntC 3.14120S 1 12235Q 2.733/57 □.0203L0GQ<1) 0.398335 □.073791 5.056234 0.0D07LOGpQ)□.2347510 109747 2.139009 □.□611R-squared0.739B93 Mean dep erident var7 700532Adjusted P-eqjared □.68iaJ7S. D. dependent var □.156574S.E.. of regression □.088316Akaike info criterion -1.803431Surn squared resid 0 070197 Schw/arz criterion -1 6S2255Log likelihood 13.62089F-stati5tic127872EDurbin^Watson stS 1.29S4J9 P rQl5(F-£lati&tic]□ 002343同样地,在Sample菜单里,把sample值改为“ 20 31”再用OLS方法进行第二个子样本回归估计,估计结果如表 4.3 0表4.3DependeM Vari^blst LCiG(Y) Melhod: Least Squares Date: 06/13/11 Time- 03:04 Sample:20 31Included observations:12Viiriflible Coefficient3td・ Error^Statistic Prob.C 3 9535441,504054211970S n.QG31LOG 佐1) -0.1137560.1593S2 -0711205 0/1950LOG[X2) 0.5201500.111654 5.55^3300.0004R-squared□ 375931Mean d&pendent var 3 23974GAdjusted F?-sqjared□.□495323D dep endent 即a「□ 3756123*E. of regression □.145754Akaike info 匚rite■0.001473Stm squared res id □.191197Sch*/arz criterion ■□.680251Log likelihood 7.m0SS F-etatiet ic32 05435Dtrbin-Watson stat 2.565362 P no b(F-statistic;)□.000030(3)求F统计量值。
(1.87)(-2.09) (-1.01) (2.56) (1.58) (0.47)基于表4.2和表4.3中残差平方和RSS 的数据,即Sum squared resid 的值, 得到 RSS1=0.0702和 RSS2=0.1912 根据 Goldfeld-Quanadt 检验,F 统计量为: F= RSS2/RSS1=0.1912/0.0702=2.73(4)判断。
在5%与 10%的显著性水平下,查F 分布表得:自由度为(9,9)的F 分布的 临界值分别为 F 0.05=3.18 与 F 0.10=2.44。
因为 F=2.73v F 0.05(9,9)=3.18,因此 5%显 著性水平下不拒绝两组子样方差相同的假设,但 10%显著性水平下拒绝两组子样方差相同的假设,(三)White 检验①由表4.1的估计结果,按heteroskedasticity (cross terms ) 进入 White 检验,其中 cross terms 表示有交叉乘 积项。
得到表4.4的结果。
表4.4WhiTa Het3「05ksdas :lii :ity Test:F-StStiGtiC9.333740 Probability□ 000027 Ob s*F?-sq Jared2D.65D35Probabiilirt /0,000935Test Equation ;Dependent Variable: RESID 吩Method: Least SquaresDale: 05/13/11 Time: 01:13Sample: 1 31Included observations' 31Variable CoelTiciertStd. Error b Statistic ProLC 1D.2432S 5.474522 1.371082 0.0/31 LOGpC)■2.329070 1.116442 ■2 086153 □.□473 (LOG pci ))^20.149114 0.053107 2 565195 00157 (LOG/叭 OG(X2))0.019333 0.041265 0.463507 □.5435 LOGpQ -0.457307 □.J5JD2D -1.007233 0.3235 〔LOG (X2〕)a □.021101 □.0133571.57969A □ 1267R-squared0 562931 Mean deperident var 0 026959 Adjusted P-sqjared □ 595517 S D. dependent var□ 042129 S.E. of regression □ 026794 Akaike info triteriori -4 239312 Sum squared resid 0.017940 Schw/arz criterion -3 9E17SG Log likelihood 71.55434 F-stat istic9.333740 Durbin^Watson st$t1.462377 Prob (F-stat istic}□.000027辅助回归结果为:F=2.73> F o.1o (9,9)=2.44,因此即存在异方差。