当前位置：文档之家 › eviews异方差、自相关检验与解决办法

eviews异方差、自相关检验与解决办法

  • 格式：doc
  • 大小：28.50 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

eviews时间序列一阶自相关检验命令

eviews时间序列一阶自相关检验命令

eviews时间序列一阶自相关检验命令在EViews中，我们可以使用AR（p）模型来进行时间序列的一阶自相关检验。

AR（p）模型表示自回归模型，其中p表示阶数。

一阶自相关检验是用来确定时间序列数据是否存在自相关性。

自相关是指序列中一个值与其在时间上前一时刻的值之间的相关性。

在时间序列分析中，我们希望序列的值是彼此相互独立的，因此自相关性可能会影响我们对序列的分析和预测。

在EViews中，可以通过以下步骤来进行一阶自相关检验：1.打开EViews软件并导入时间序列数据。

2.在EViews主菜单中选择“Quick/Estimate Equation”（快速估计方程）。

3.在“Equation Specification”（方程规范）对话框中，输入要估计的模型。

例如，如果要进行一阶自相关检验，则可以输入模型“y c ar(1)”。

- “y”表示被解释变量。

- “c”表示常数项。

- “ar(1)”表示自回归项，其中1表示阶数。

4.单击“OK”按钮以估计模型。

5.将结果显示为估计方程的系数，t统计量，R-squared（R平方值）等。

在估计方程后，EViews将为我们提供一阶自相关检验的结果。

重要的统计值包括Jarque-Bera（JB）统计量、ARCH LM检验、DW统计量等。

- Jarque-Bera（JB）统计量是用来检验数据是否服从正态分布。

如果JB统计量的p值小于0.05，则我们可以拒绝原假设，即数据不服从正态分布。

- ARCH LM检验旨在检验序列中是否存在异方差性。

如果ARCH LM 统计量的p值小于0.05，则我们可以拒绝原假设，即序列中存在异方差性。

- Durbin-Watson（DW）统计量是用来检验序列的自相关性。

DW统计量的值介于0和4之间，如果DW值接近于2，则表示序列不存在一阶自相关。

除了上述统计量之外，EViews还提供了其他有关模型估计的信息，包括系数的标准误差、置信区间、F统计量和R平方等。

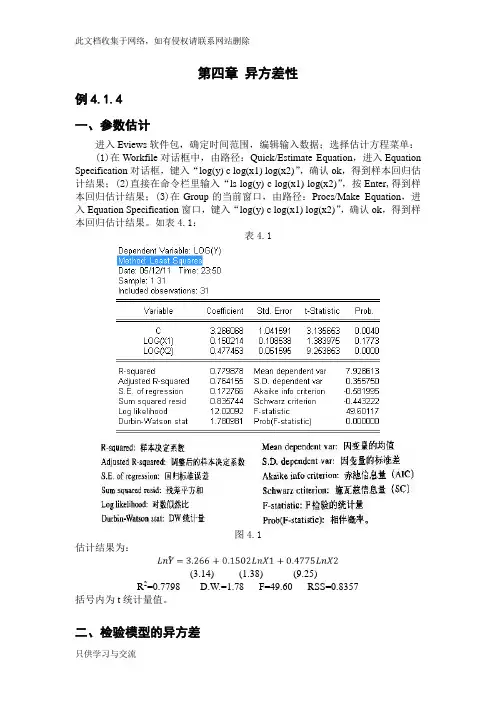
第四章异方差检验的eviews操作

第四章异方差检验的eviews操作

第四章异方差性例4.1.4一、参数估计进入Eviews软件包，确定时间范围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表4.1：表4.1图4.1估计结果为：(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation 对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图4.2。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter，可得散点图4.2。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图4.2。

eviews异方差的检验

eviews异方差的检验

田青帆1006010131 国贸1001班建立模型Y t=β1+β2X t+uX:1994-2011年中国国内生产总值Y:1994-2011年中国进口总额数据来源：国泰安数据服务中心/p/sq/一、异方差的检验1、图示法由上图可以看出，残差平方项e2随X的变动而变动，一次，模型很可能存在异方差，但是否确实存在异方差还应通过更进一步的检验。

2、等级相关系数检验t值为29.48788，自由度为18-2=16在95%的显著水平下，查表可得t0.025(16)=2.1199t＞t0.025(16),说明X i和｜e i｜之间存在系统关系，则说明模型中存在异方差3、戈德菲尔德-夸特检验（样本分段比检验）在本例中，样本容量为18，删去中间4个观测值，余下部分平分的两个样本区间：1-7和12-18，他们的样本数都是7个，用OLS方法对这两个子样本进行回归估计，结果如下图所示计算检验统计量FF=[RSS２/(n２-k)] ÷[RSS１/(n１-k)]n2-k=n1-k=7-2=5F=RSS2/RSS1=4588102/229037.4=20.03在95%的显著水平下，查表可得F0.05（5，5）=5.05 F＞F0.05（5，5）所以，模型存在异方差4、戈里瑟（Glejser）检验用残差绝对值建立的回归模型为｜e i｜=α1+α2 (1/X i)由上表可知，回归模型为｜e i｜=1416.049+10.37101(1/X i)≠0，则存在异方差α25、怀特检验由上图可知：P值=0.017140﹤0.05，所以存在异方差二、异方差的修正（加权最小二乘法）1、选择1/x为权数，即对模型两边同时乘以1/x，使用最小二乘法进行回归估计，所得结果如下：由上图可知，P值=0.0001﹤0.05，模型依然存在异方差2、选择1/|e|为权数，即对模型两边同时乘以1/|e|，使用最小二乘法进行回归估计，所得结果如下：此时，P值=0.2139＞0.05，将异方差模型变成了同方差。

第四章 异方差检验的eviews操作

第四章 异方差检验的eviews操作

第四章异方差性例4.1.4一、参数估计进入Eviews软件包，确定时间范围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表4.1：表4.1图4.1估计结果为：(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图4.2。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter，可得散点图4.2。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图4.2。

异方差检验的eviews操作

异方差检验的eviews操作

第四章异方差性例4.1.4一、参数估计进入Eviews软件包，确定时间范围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表4.1：表4.1图4.1估计结果为：(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图4.2。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter ，可得散点图4.2。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图4.2。

实验二 异方差、序列相关的检验及修正

实验二 异方差、序列相关的检验及修正

实验二：异方差和自相关模型的检验和处理二、实验目的(1) 熟悉EViews软件在自相关模型中的根本使用方法；(2) 掌握异方差、自相关模型的检验和处理方法；三、实验的软硬件环境要求硬件环境要求：科学计算与经济分析实验室，计算机网络设备，需要连接Internet使用的软件名称、版本号以及模块带Windows操作系统以及EViews应用演示软件。

四、知识准备前期要求掌握的知识：了解EViews软件在自相关和异方差分析中的根本概念和根本功能，理解违背线性回归模型的根本假设中的自相关和异方差产生的原因，解决这两类问题的根本理论。

实验相关理论或原理：(1)理解线性模型违背根本假设：误差项同方差性、无序列相关性的含义及其在实际经济问题中产生的原因；(2)掌握线性模型异方差性和序列相关性的检验的统计思想和EViews实现。

(3) 掌握线性模型异方差性和序列相关性的处理方法统计思想和EViews实现。

实验流程：线性回归模型假设→线性回归模型异方差和序列相关性检验→线性回归模型异方差和序列相关性的处理→线性回归模型的修正。

五、实验材料和原始数据表2.1 各地区农村居民家庭人均纯收入与消费支出〔单位：元〕表2.2 1978~2001年中国商品进口与国内生产总值六、实验要求和考前须知能用EViews软件完成线性回归模型的异方差和序列相关性的检验和处理，以及对模型的修正。

能对软件输出的结果能做较详细的分析，能结合数据提出自己的见解。

七、实验内容及步骤〔一〕异方差1.加载工作文件。

(1)建立工作文件的方法是点击,选择新建对象类型为工作文件，选择数据类型，注意本数据是截面数据。

建立工作文件，建立新序列，建立空组。

创立三个序列Y(人均消费支出)、X1(从事农业经营的收入)、X2(其他收入)并输入数据。

进入界面后输入数据如图3－1，3-2所示。

图3－1 图3－22.选择方程〔1〕根据消费理论，中国农村居民人均消费主要由人均纯收入决定，为了考察从事农业经营的收入和其他收入对农村居民消费支出增长的影响，考虑双对数模型：01122ln ln ln Y X X βββμ=+++〔2〕先对模型进展估计。

eviews的异方差检验

eviews的异方差检验
eviews的异方差检验
异方差的处理
文档附赠有可编辑的3D小人素材
地区
北京 天津 河北 山西 内蒙古 辽宁 吉林 黑龙江 上海 江苏 浙江 安徽 福建 江西 山东
农业总产值 亿元 115.48 117.60
1639.07 322.65 620.42 837.50 641.50 971.94 126.74 1542.53 735.92 1054.01 685.30 621.26 2604.07
,所以存在异方差性。 ⒊White检验 ⑴建立回归模型：LS Y C X,回归结果如图6。
图6
⑵在方程窗口上点击View\Residual Test\ White Heteroskedastcity no cross terms ,检验结果如 图7。
图7
直接观察相伴概率p值的大小,若p值较小,则认为存 在异方差性。 ⒋Park检验 ⑴建立回归模型 结果同图6所示 。 ⑵生成新变量序列：GENR LNE2=log RESID^2
SMPL 20 31 LS Y C X
图5
⑷计算F统计量：F R2 /S R1 S S 2S 2/6 35.9 8 1 6 .4 5
RSS1 和RSS2分别是模型1和模型2的残差平方和。 取
F6.4 5F 0.05 2.98
F 0 .0( 1 5 1 2 1 ,1 1 2 1 ) 2 .98
农业总产值 亿元
1152.09 1243.15 1328.70 970.55 224.17 401.48 1316.60 392.20 683.80 39.49 629.34 458.73 49.16 111.12 767.00
农作物播种面 积 千公顷 7030.01 7390.71 4363.05 5594.40 754.32 3134.66 9278.24 4464.53 5801.86 232.92 4044.74 3759.00 516.68 1189.83 4202.63

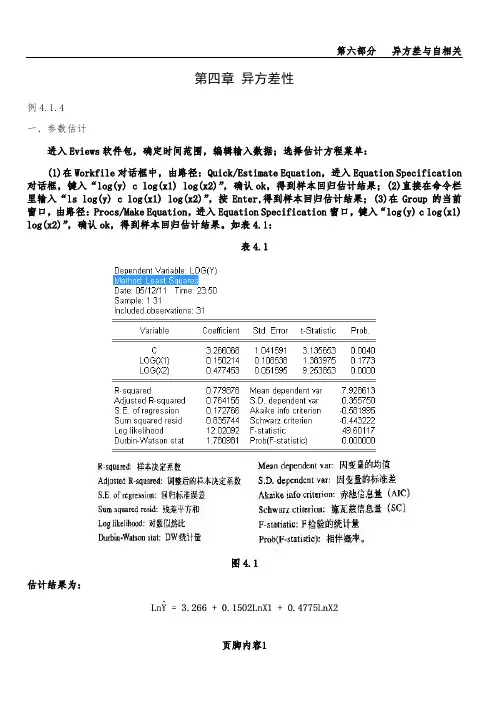
异方差检验的eviews操作

异方差检验的eviews操作

第四章异方差性例4.1.4一、参数估计进入Eviews软件包，确定时间范围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification 对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表4.1：表4.1图4.1估计结果为：(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图4.2。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter ，可得散点图4.2。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图4.2。

异方差检验的eviews操作

异方差检验的eviews操作

第四章异方差性例4.1.4一、参数估计进入Eviews软件包，确定时间范围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表4.1：表4.1图4.1估计结果为：(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图4.2。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter，可得散点图4.2。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图4.2。

异方差检验的eviews操作

异方差检验的eviews操作

第四章异方差性例一、参数估计进入Eviews软件包，确定时间范围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表：表图估计结果为：R2= .= F= RSS=括号内为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter ，可得散点图。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图。

图由图可以看出，残差平方项e2对解释变量log(X2)的散点图主要分布图形中的下三角部分，大致看出残差平方项e2随log(X2)的变动呈增大的趋势，因此，模型很可能存在异方差。

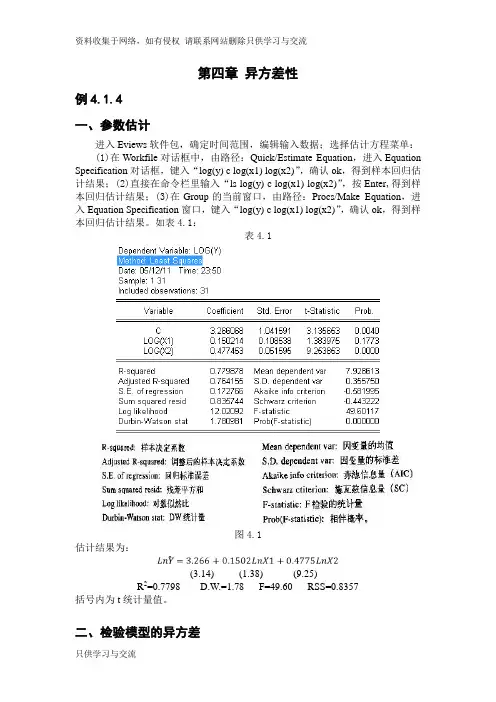
异方差检验的eviews操作

异方差检验的eviews操作

第四章异方差性例4.1.4一、参数估计进入Eviews软件包，确定时间范围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表4.1：表4.1图4.1估计结果为：(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图4.2。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter，可得散点图4.2。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图4.2。

计量经济学实验报告-异方差问题white分析

计量经济学实验报告-异方差问题white分析
3.运用Gleser法，检验异方差问题。并解释相关变量。
4.运用对数方法，消除异方差问题。进行多元线性回归分析并呈现结果，并解释相关变量。
5.运用WLS方法，消除异方差问题。进行多元线性回归分析并呈现结果，并解释相关变量。
实验内容\步骤
1.打开eviews，点击Open a Foreign file，选择桌面上保存好的练习数据，点击选择Quick-Generate Series菜单命令，在弹出的对话框中输入e=resid，生成残差序列。然后选择Quick-Graph菜单命令，在弹出的对话框中输入变量名x e^2，得到散点图。
Std. Error
t-Statistic
Prob.
C
-15.32732
1.507305
-10.16869
0.0000
LOG(X)
2.224390
0.151781
14.65526
0.0000
R-squared
0.881039
Mean dependent var
6.740001
Adjusted R-squared
实验结果分析及讨论（续）
4.运用对数方法，消除异方差结果如下：
Dependent Variable: LOG(Y)
Method: Least Squares
Date: 10/12/21 Time: 20:18
Sample: 1 31
Included observations: 31
Variable
Coefficient
Dependent Variable: Y
Method: Least Squares
Date: 10/12/21 Time: 20:25

Eviews数据统计与分析教程9章条件异方差模型ARCHGARCH

Eviews数据统计与分析教程9章条件异方差模型ARCHGARCH

EViews统计分析基础教程
三、ARCH模型的其他扩展形式
2. TARCH模型
TARCH（Threshold ARCH）模型是门限自回归条件异 方差模型，可用来分析数据的剧烈波动性。 模型中条件方差的形式为
其中，dt-1是一个虚拟变量，满足的条件为 1 ，如果μt-1<0
dt-1= 0，如果μt-1>=0
EViews统计分析基础教程
一、自回归条件异方差模型（ARCH）
2.ARCH模型检验
（2）残差平方的相关图（Q）检验法
在EViews操作中，要实现残差平方的相关图（Q）检验，需 在 方 程 对 象 窗 口 中 选 择 “ View”|“Residual Tests”|“Correlogram – Q – statistics”选项。
GARCH（1，1）模型在金融领域应用广泛，可以对金融时 间序列的数据进行描述。
EViews统计分析基础教程
二、广义自回归条件异方差模型（GARCH）
2.GARCH模型的建立
当上述辅助回归方程进行ARCH效应检验时，如果ARCH的 滞后阶数q很大，检验结果依然显著，即残差序列依然存在 ARCH（q）效应。此时可采用GARCH（p，q）模型重新进 行估计。
在“Options”中输入ARCH和GARCH的阶数 。
在“Variance”的编辑栏中可列出方差方程中的外生变量。
EViews统计分析基础教程
一、自回归条件异方差模型（ARCH）
3.ARCH模型的建立
Options选项卡
如果选中“Backcasting”（回推） 中的复选框，MA初始扰动项 和GARCH项中的初始预测方 差将使用回推（“Backcasting”） 方法确定初始值。

检验和消除异方差和自相关的报告

检验和消除异方差和自相关的报告

消除异方差和自相关的实验报告【实验内容】通过查询中国统计局的2012年中国统计年鉴及新浪财经数据网，获得1980年--2012年各项指标的数据，如下表所示:年份Y-出口贸易总额（亿美元）X-外商直接投资（亿美元）1980181.19 3.54 1981220.10 3.54 1982223.20 3.54 1983222.309.20 1984261.4014.20 1985273.5019.56 1986309.4022.44 1987394.4023.14 1988475.2031.94 1989525.4033.92 1990620.9134.87 1991719.1043.66 1992849.40110.08 1993917.44275.15 19941210.06337.67 19951487.80375.21 19961510.48417.26 19971827.92452.57 19981837.09454.63 19991949.31403.1920002492.03407.1520012660.98468.7820023255.96527.4320034382.28535.0520045933.26606.3020057619.53603.2520069689.36630.21200712177.76747.68200814306.93923.95200912016.12900.33201015779.301057.40201118986.001160.23201220489.301116.16【实验步骤——检验并消除异方差】一检查模型是否存在异方差性1、图形分析检验（1）散点相关图分析做出外商直接投资X与出口贸易总额Y的散点图（SCAT X Y）。

观察相关图可以看出，随着外商直接投资的增加，出口贸易总额的平均水平不断提高，但离散程度也逐步扩大。

这说明变量之间可能存在递增的异方差性。

异方差进行检验和补救

异方差进行检验和补救

实验报告课程名称：计量经济学实验项目名称：单方程线性回归模型中异方差的检验与补救院（系）：经济与管理学院专业班级：09国贸一班姓名：卢娟学号：0965137115实验地点：经管机房实验日期：2012 年 5 月7 日实验目的：掌握利用EViews软件对模型中存在的异方差进行检验和补救。

实验内容：根据我国2000年部分地区城镇居民每个家庭平均全年可支配收入X与消费支出Y 的统计数据，通过建立双变量线性回归模型分析人均可支配收入对人均消费支出的线性影响，并讨论异方差的检验与修正过程。

1、异方差的检验1）图示法2）Park检验3）Glejser检验4）Goldfeld-Quandt检验5）White检验2、异方差的补救1）加权最小二乘法（WLS）2）对数变换实验方法、步骤和结果：案例：沿用研究印度食物支出和总支出关系的例子，通过建立双变量线性回归模型分析印度总支出对食物支出的线性影响，并讨论异方差的检验与修正过程。

1、异方差的检验打开Eviews5，建立新的工作文件，选择横截面数据，观察项为55，并复制数据，进行重命名。

1）图示法A、用X-Y的散点图进行判断以组的形式打开XY, view,graph ,scatter ,simple scatter,得到散点图分析：散点图在越靠后的位置，离散程度越大，模型可能存在异方差。

B、用Y的估计值与残差平方的散点图进行判断做一个55个变量的回归，点击quick, estimate equation ,输入公式y c x,得到回归，点击forcast得到Y的估计值。

点击proc,make residual series，将名字改为res，生成残差序列。

点击quick ,graph, scatter ,输入yf res^2，得到散点图分析：没有生成一条斜率为0的直线，而且，散点图月靠后的位置，离散程度越大，所以，模型可能存在异方差。

C、用任一解释变量X与残差平方的散点图进行判断。

第四章 异方差检验的eviews操作

第四章 异方差检验的eviews操作

第四章异方差性例一、参数估计进入Eviews软件包，确定时间范围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表：表图估计结果为：R2= .= F= RSS=括号内为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter ，可得散点图。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图。

图由图可以看出，残差平方项e2对解释变量log(X2)的散点图主要分布图形中的下三角部分，大致看出残差平方项e2随log(X2)的变动呈增大的趋势，因此，模型很可能存在异方差。

第四章 异方差检验的eviews操作

第四章 异方差检验的eviews操作

第四章异方差性例4.1.4一、参数估计进入Eviews软件包，确定时间范围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表4.1：表4.1图4.1估计结果为：LnŶ=3.266+0.1502LnX1+0.4775LnX2(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图4.2。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter，可得散点图4.2。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图4.2。

异方差检验的eviews操作

异方差检验的eviews操作

第四章异方差性例4.1.4一、参数估计进入Eviews软件包，确定时间围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表4.1：表4.1图4.1估计结果为：(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图4.2。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter ，可得散点图4.2。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图4.2。

计量经济学EVIEWS自相关检验与修正

计量经济学EVIEWS自相关检验与修正

一、数据来源
数据：国家统计局（1981~2010年国内生产总值与固定资产投资）软件版本：EVIEWS7.2
二、回归结果
1、一元线性回归：
三、模型诊断与修正
DW检验：相关系数δ=0.8546，查表得，
1.35
1.49
L
U
d
d
=
=
经检验，DW<1.35,自变量呈一阶正自
相关
四、广义差分法修正后的结果
对E 进行滞后一期的自回归，可得回归方程：E=0.9337E(-1)
对原模型进行广义差分，输出结果为：
**ˆˆ6981.723 1.002749t t y x =+
由于使用广义差分数据，样本容量减少了1个，为29个。

查5%的显著性水平的DW
统计表可知， 1.341.48
L U d d ==，模型中的4-DU>DW>DU ，所以广义差分模型已无序列相关。

根据()1ˆˆ16981.723βρ-=，可得1
ˆ=105305.023β。

因此，原回归模型应为 105305.023 1.002749t t y x =+
采用普莱斯-文斯滕变换后第一个观测值变为211y δ-为1750.7019和211x δ-为344.1377，变换后普通最小二乘结果为**ˆˆ7555.503 1.0611t t y
x =+，根据()1ˆˆ17555.503βρ-=，得1
ˆ=113959.321β，由此，最终模型是 ˆ113959.321 1.0611t t y
x =+。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

eviews异方差、自相关检验与解决办法
一、异方差检验：
1．相关图检验法
LS Y C X 对模型进行参数估计
GENR E=RESID 求出残差序列
GENR E2=E^2 求出残差的平方序列
SORT X 对解释变量X排序
SCAT X E2 画出残差平方与解释变量X的相关图
2．戈德菲尔德——匡特检验
已知样本容量n=26，去掉中间6个样本点（即约n/4），形成两个样本容量均为10的子样本。

SORT X 将样本数据关于X排序
SMPL 1 10 确定子样本1
LS Y C X 求出子样本1的回归平方和RSS1
SMPL 17 26 确定子样本2
LS Y C X 求出子样本2的回归平方和RSS2
计算F统计量并做出判断。

解决办法
3．加权最小二乘法
LS Y C X 最小二乘法估计，得到残差序列
GRNR E1=ABS(RESID) 生成残差绝对值序列
LS(W=1/E1) Y C X 以E1为权数进行加权最小二成估计
二、自相关
1．图示法检验
LS Y C X 最小二乘法估计，得到残差序列
GENR E=RESID 生成残差序列
SCAT E(-1) E et—et-1的散点图
PLOT E 还可绘制et的趋势图
2．广义差分法
LS Y C X AR(1) AR(2)
首先，你要对广义差分法熟悉，不是了解，如果你是外行，我奉劝你还是用eviews来做就行了，其实我想老师要你用spss无非是想看你是否掌握广义差分，好了，废话不多说了。

接着，使用spss16来解决自相关。

第一步，输入变量，做线性回归，注意在Liner Regression 中的Statistics中勾上DW，在save中勾Standardized，查看结果，显然肯定是有自相关的（看dw值）。

第二步，做滞后一期的残差，直接COPY数据（别告诉我不会啊），然后将残差和滞后一期的残差做回归，记下它们之间的B指（就是斜率）。

第三步，再做滞后一期的X1和Y1，即自变量和因变量的滞后一期的值，也是直接COPY。

第四步，最后定义两个新变量，即X2=X-B*X1，Y2=Y-B*X2，最后做X2和Y2的回归，这样广义差分就完成了。

但是这仅仅只是一次广义差分，观察X2和Y2的回归分析表，如果DW值仍然显示有自相关，则还要做一次差分，即重复上述步骤即可。

一般来说，广义差分最多做2次就行了。

本文来自: 人大经济论坛SPSS专版版，详细出处参考：/forum.php?mod=viewthread&tid=289529&page=1。