最新eviews的异方差检验

eviews异方差检验步骤Eviews是一款常用的经济学软件，它允许用户进行多种统计分析，其中包括异方差检验。

异方差是指随着自变量的变化，因变量的方差也会发生变化。

在实际分析中，如果忽略了异方差，则会导致统计结果不准确。

因此，在使用Eviews进行分析时，进行异方差检验十分重要。

以下是Eviews进行异方差检验的步骤：1. 打开Eviews软件，并导入所需的数据。

在“工作文件”菜单下选择“打开文件”，找到所需的数据文件并打开。

2. 选择变量。

单击“变量”菜单，并选择要检验的因变量和自变量。

如果有多个自变量，在本例中就需要选择多个自变量。

3. 进行回归分析。

单击“Quick”菜单下的“Estimate Equation”选项，进行回归分析。

在回归分析中，需要输入因变量和自变量，并进行模型估计。

4. 异方差检验。

在回归分析完成后，单击“View”菜单下的“Residual Diagnostics”选项，进入错误项诊断。

5. 在错误项诊断中选择异方差检验。

在错误项诊断面板中，选择“Heteroskedasticity Tests”选项，并选择所需的异方差检验类型。

在Eviews中，通常可以使用Breusch-Pagan/Godfrey测试或White 测试来检验异方差。

6. 查看结果。

完成异方差检验后，Eviews会返回检验结果。

如果结果显示存在异方差，则需要进行调整，以消除异方差的影响。

总之，在使用Eviews进行经济学分析时，进行异方差检验至关重要，可以保证模型分析的准确性和可靠性。

上述步骤简单易懂，只要按照步骤操作，就可以轻松地完成异方差检验。

eviews异方差检验步骤Eviews异方差检验步骤异方差是指随着自变量的变化，因变量的方差也会发生变化。

在回归分析中，如果存在异方差，会导致回归系数的估计值不准确，从而影响模型的可靠性。

因此，进行异方差检验是非常重要的。

Eviews是一款常用的统计软件，它提供了多种方法来检验异方差。

下面我们将介绍Eviews中进行异方差检验的步骤。

步骤一：建立回归模型我们需要建立一个回归模型。

在Eviews中，可以通过“Quick”菜单中的“Estimate Equation”来建立回归模型。

在弹出的对话框中，选择因变量和自变量，并设置其他参数，如拟合方法、截距项等。

步骤二：检验异方差建立好回归模型后，我们需要进行异方差检验。

在Eviews中，可以通过“View”菜单中的“Residual Diagnostics”来进行检验。

在弹出的对话框中，选择“Heteroskedasticity Tests”选项卡，然后选择需要进行的异方差检验方法。

Eviews提供了多种异方差检验方法，包括Breusch-Pagan-Godfrey 检验、White检验、Goldfeld-Quandt检验等。

这些方法的原理和适用条件不同，需要根据具体情况选择合适的方法。

步骤三：解释检验结果进行异方差检验后，Eviews会输出检验结果。

通常包括检验统计量、p值等信息。

如果p值小于显著性水平（通常为0.05），则可以拒绝原假设，认为存在异方差。

如果检验结果显示存在异方差，我们需要对模型进行修正。

常用的方法包括使用异方差稳健标准误、进行加权最小二乘回归等。

总结Eviews提供了多种方法来检验异方差，包括Breusch-Pagan-Godfrey检验、White检验、Goldfeld-Quandt检验等。

进行异方差检验后，需要根据检验结果对模型进行修正，以提高模型的可靠性。

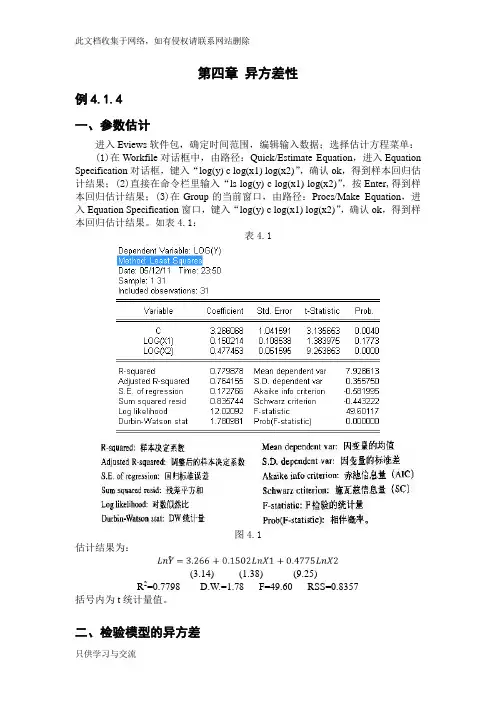
第四章异方差性例4.1.4一、参数估计进入Eviews软件包，确定时间范围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表4.1：表4.1图4.1估计结果为：(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation 对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图4.2。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter，可得散点图4.2。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图4.2。

第四章异方差性例4.1.4一、参数估计进入Eviews软件包，确定时间范围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表4.1：表4.1图4.1估计结果为：(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图4.2。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter，可得散点图4.2。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图4.2。

第四章异方差性例4.1.4一、参数估计进入Eviews软件包，确定时间范围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表4.1：表4.1图4.1估计结果为：(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图4.2。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter ，可得散点图4.2。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图4.2。

案例2：利用Eviews4.0检验和消除异方差 一、实验目的本实验着重介绍如何检模型中是否存在异方差，如果存在自相关应该如何消除异方差。

二、本实验的主要步骤该实验主要的步骤可以用如下的框图来表示：三、一个示例为了了解某社区居民的消费情况，现从该社区随机抽取了35个家庭，取得了如下的一组数据，其中X 为可支配收入，Y 为消费性支出，试建立两者适当的回归模型，然后检验该模型是否存在异方差，如果存在异方差，请设法消除异方差。

X 1386.10 958.87 803.65 1143.23 2148.23 961.54 1114.11 1542.58 1200.28 Y 991.85 723.42 641.09 904.84 2106.02 900.84 913.08 1120.30 881.47 X 963.62 2089.99 1061.86 1187.20 2499.90 2194.69 1819.52 1457.14 944.28 Y 890.94 1712.49 952.36 845.29 2348.21 2036.46 1306.84 1214.63 751.32 X 912.00 1432.82 922.04 1063.76 893.70 1193.40 1684.75 1931.58 1993.19 Y 786.79 1000.25 710.30 1010.86 852.14 1132.18 1463.39 1677.38 1403.99 X 1548.98 968.36 894.15 1931.02 1035.20 2260.95 2065.01 1084.21 Y 1190.10 791.05 858.10 1512.94 807.16 2240.59 1529.55 972.27 解：1、首先建立一个工作文件，采用命令方法为：WORKFILE MYFILE U 1 35建立一个MFFILE 的工作文件，然后输入变量数据，命令为：DATA X Y其中Y 代表支出，X 代表收入。

第四章异方差性例4.1.4一、参数估计进入Eviews软件包，确定时间范围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification 对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表4.1：表4.1图4.1估计结果为：(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图4.2。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter ，可得散点图4.2。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图4.2。

第四章异方差性例4.1.4一、参数估计进入Eviews软件包，确定时间范围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表4.1：表4.1图4.1估计结果为：(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图4.2。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter，可得散点图4.2。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图4.2。

EViews计量经济学实验报告异⽅差的诊断及修正姓名学号实验题⽬异⽅差的诊断与修正⼀、实验⽬的与要求：要求⽬的：1、⽤图⽰法初步判断是否存在异⽅差，再⽤White检验异⽅差；2、⽤加权最⼩⼆乘法修正异⽅差。

估计结果为： iY ? = 12.03564 + 0.104393i X （19.51779） (0.008441) t=（0.616650）（12.36670）2R =0.854696 R =0.849107 S.E.=56.89947 DW=1.212859 F=152.9353这说明在其他因素不变的情况下，销售收⼊每增长1元，销售利润平均增长0.104393元。

2R =0.854696 , 拟合程度较好。

在给定 =0.0时，t=12.36670 > )26(025.0t =2.056 ，拒绝原假设，说明销售收⼊对销售利润有显著性影响。

F=152.9353 > )6,21(F 05.0= 4.23 ,表明⽅程整体显著。

（三）检验模型的异⽅差※（⼀）图形法6、判断由图3可以看出，被解释变量Y 随着解释变量X 的增⼤⽽逐渐分散，离散程度越来越⼤；同样，由图4可以看出，残差平⽅2 i e 对解释变量X 的散点图主要分布在图形中的下三⾓部分，⼤致看出残差平⽅2i e 随i X 的变动呈增⼤趋势。

因此，模型很可能存在异⽅差。

但是否确实存在异⽅差还应该通过更近⼀步的检验。

※（⼆）White 检验White 检验结果White Heteroskedasticity Test:F-statistic3.607218 Probability 0.042036 Obs*R-squared6.270612 Probability0.043486Test Equation:t 界值5.002χ（2）=5.99147。

⽐较计算的2χ统计量与临界值，因为n 2R = 6.270612 > 5.002χ（2）=5.99147 ，所以拒绝原假设，不拒绝备择假设，这表明模型存在异⽅差。

eviews异方差、自相关检验与解决办法一、异方差检验：1．相关图检验法LS Y C X 对模型进行参数估计GENR E=RESID 求出残差序列GENR E2=E^2 求出残差的平方序列SORT X 对解释变量X排序SCAT X E2 画出残差平方与解释变量X的相关图2．戈德菲尔德——匡特检验已知样本容量n=26，去掉中间6个样本点（即约n/4），形成两个样本容量均为10的子样本。

SORT X 将样本数据关于X排序SMPL 1 10 确定子样本1LS Y C X 求出子样本1的回归平方和RSS1SMPL 17 26 确定子样本2LS Y C X 求出子样本2的回归平方和RSS2计算F统计量并做出判断。

解决办法3．加权最小二乘法LS Y C X 最小二乘法估计，得到残差序列GRNR E1=ABS(RESID) 生成残差绝对值序列LS(W=1/E1) Y C X 以E1为权数进行加权最小二成估计二、自相关1．图示法检验LS Y C X 最小二乘法估计，得到残差序列GENR E=RESID 生成残差序列SCAT E(-1) E et—et-1的散点图PLOT E 还可绘制et的趋势图2．广义差分法LS Y C X AR(1) AR(2)首先，你要对广义差分法熟悉，不是了解，如果你是外行，我奉劝你还是用eviews来做就行了，其实我想老师要你用spss无非是想看你是否掌握广义差分，好了，废话不多说了。

接着，使用spss16来解决自相关。

第一步，输入变量，做线性回归，注意在Liner Regression 中的Statistics中勾上DW，在save中勾Standardized，查看结果，显然肯定是有自相关的（看dw值）。

第二步，做滞后一期的残差，直接COPY数据（别告诉我不会啊），然后将残差和滞后一期的残差做回归，记下它们之间的B指（就是斜率）。

第三步，再做滞后一期的X1和Y1，即自变量和因变量的滞后一期的值，也是直接COPY。

第四章异方差性例4.1.4一、参数估计进入Eviews软件包，确定时间范围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表4.1：表4.1图4.1估计结果为：(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图4.2。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter，可得散点图4.2。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图4.2。

实验一异方差性【实验目的】掌握异方差性问题出现的来源、后果、检验及修正的原理，以及相关的Eviews操作方法。

【实验内容】以《计量经济学学习指南与练习》补充习题4-16为数据，练习检查和克服模型的异方差的操作方法。

【4-16】表4-1给出了美国18个行业1988年研究开发（R&D）费用支出丫与销售收入X 的数据。

请用帕克（Park）检验、戈里瑟（Gleiser）检验、G-Q检验与怀特（White）检验来检验丫关于X的回归模型是否存在异方差性？若存在异方差性，请尝试消除它。

【实验步骤】一■检查模型是否存在异方差性1、图形分析检验（1）散点相关图分析做出销售收入X与研究开发费用丫的散点相关图（SCAT X 丫）。

观察相关图可以看出，随着销售收入的增加，研究开发费用的平均水平不断提高，但离散程度也逐步扩大。

这说明变量之间可能存在递增的异方差性。

0 50,000 100,000 150,000 200.000 250,000(2)残差图分析首先对数据按照解释变量X 由小至大进行排序(SORT X )，然后建立一元线 性回归方程(LS 丫 C X )。

Dependentvariable: Y Method: Least Squares Date: 12/06/11 Time ： 23:08 Sample: 1 17Included obseivations: 17VariableCo EfficientStd. Errort-StallStic Prob C 187.5068 1106.681 0.169432 0.8677 X0.031993 0.0111112 8793580.0115 R-squared0.355966 Mean dependent var 2676.188 Adjusted R-squared 0.313031 S.D. dependent var3438.207 S.E. of regression 2849711 Aka ike Info criterion 13.85795 Sum squared resid 1 22E+O0 Schwarz criterion 18.95698 Log likelihood -158.2926 Hannan-Quinn criter. 18.86770 F-statistic8.290703 Durbin-Watson stat2.738533Prob(F-statistic)0.011464因此，模型估计式为：丫 =187.507 0.032* X ------- (*)2 (0.17)(2.88)R 2=0.31s.e.=2850F=0.011建立残差关于X 的散点图，可以发现随着X 增加，残差呈现明显的扩大 趋势，表明存在递增的异方差。

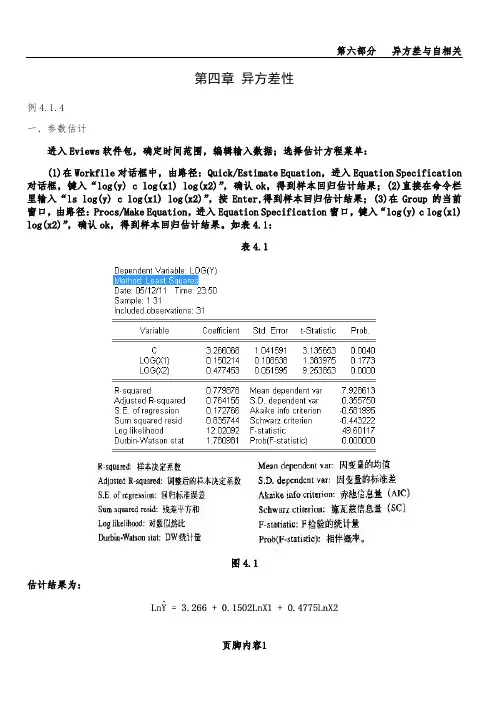
第四章异方差性例4.1.4一、参数估计进入Eviews软件包，确定时间范围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表4.1：表4.1图4.1估计结果为：LnŶ=3.266+0.1502LnX1+0.4775LnX2(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号内为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图4.2。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter，可得散点图4.2。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图4.2。

第四章异方差性例4.1.4一、参数估计进入Eviews软件包，确定时间围，编辑输入数据；选择估计方程菜单：(1)在Workfile对话框中，由路径：Quick/Estimate Equation，进入Equation Specification对话框，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果；(2)直接在命令栏里输入“ls log(y) c log(x1) log(x2)”，按Enter,得到样本回归估计结果；(3)在Group的当前窗口，由路径：Procs/Make Equation，进入Equation Specification窗口，键入“log(y) c log(x1) log(x2)”，确认ok，得到样本回归估计结果。

如表4.1：表4.1图4.1估计结果为：(3.14) (1.38) (9.25)R2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357括号为t统计量值。

二、检验模型的异方差（一）图形法（1）生成残差平方序列。

①在Workfile的对话框中，由路径：Procs/Generate Series，进入Generate Series by Equation对话框，键入“e2=resid^2”，生成残差平方项序列e2；②直接在命令栏里输入“genr e2=resid^2”，按Enter,得到残差平方项序列e2。

（2）绘制散点图。

①直接在命令框里输入“scat log(x2) e2”，按Enter，可得散点图4.2。

②选择变量名log(x2)与e2（注意选择变量的顺序，先选的变量将在图形中表示横轴，后选的变量表示纵轴），再按路径view/graph/scatter/simple scatter ，可得散点图4.2。

③由路径quick/graph进入series list窗口，输入“log(x2) e2”，确认并ok，再在弹出的graph窗口把line graph换成scatter diagram，再点ok，可得散点图4.2。