青岛版初中数学九年级上册《解直角三角形》小结与复习1
- 格式:ppt
- 大小:614.00 KB
- 文档页数:22

《解直角三角形》教案 一、学习目标 1.理解直角三角形中五个元素的关系,会运用勾股定理、直角三角形的两个锐角互余及锐角三角比解直角三角形;2.通过解直角三角形,逐步培养学生分析问题、解决问题的能力;3.渗透数形结合的数学思想,培养学生良好的学习习惯.二、重点难点重点:1.直角三角形的解法.难点:1.三角比在解直角三角形中的灵活运用.疑点:1.学生可能不理解在已知的两个元素中,为什么至少有一个是边.三、自学指导(一)回顾总结1.在三角形中共有几个元素?2.在Rt ABC 中,90C ∠=,a b c ∠∠、、、A 、B 这五个元素间有哪些等量关系呢?① 角之间的关系: .② 边之间的关系: .③ 边角之间的关系:sin A = ,cos A = ,tan A = .说明:利用这些关系,如果知道直角三角形的两个元素(至少有 ),就可以求其他的元素了.3.解直角三角形的定义:叫做解直角三角形. 四、典型例题【例1】根据下列条件解直角三角形.① 在Rt ABC 中,90C ∠=,5,52a c ==;② 在Rt ABC 中,90C ∠= ,6,23a b ==; ③ 在Rt ABC 中,90C ∠= ,43,60c A =∠= ;④ 在Rt ABC 中,90C ∠= ,15,30b A =∠= .【例2】如图所示,在ABC 中,60,45,8A B AB ∠=∠== .求ABC 的面积(结果可保留根号).【变式1】如图所示,在ABC 中,60,45,20A B AC ∠=∠== 厘米.求AB 的长.【变式2】请你画出一个以BC 为底边的等腰ABC ,使底边上的高AD BC =.① 求tan B 和sin B 的值;② 在你所画的等腰ABC 中,若5BC =,求腰上的高BE .五、对应训练1.在ABC 中,90C ∠=,已知A ∠和斜边c ,可用关系式 求出B ∠,可用关系式 求出a ,已知a 和c ,可用关系式 求出b .2.在ABC 中,90C ∠= ,30B ∠= ,23BC =,则AB 的长为 .3.如图,在ABC 中,90C ∠= ,410,sin 5AB cm A ==,则BC 的长为 cm . 4.已知Rt ABC 中,斜边AB 的长为m ,40B ∠= ,则直角边BC 的长是( )A .sin 40mB .cos 40mC .tan 40mD .tan 40m B A C5.在Rt ABC 中,90C ∠=,则下列各组等式中正确的是( ) A .tan ,sin a a b B c B ==B .,tan cos b a a c B B ==C .,sin tan b a c a B B== D .tan ,cos A b B c a B == 6. 在Rt ABC 中,90,ACB CD AB ∠=⊥ 于点D ,已知5,2AC BC ==,那么sin ACD ∠的值为( )A .53B .23C .255D .527.等边三角形的高为a ,则它的边长为( )A .33aB .233aC .32a D .2a 8.如图所示,以直角坐标系的原点O 为圆心,以1为半径作圆,若点P 是该圆上第一象限内的一点,且OP 与x 轴正方向的夹角为α,则点P 的坐标是( )A .(cos ,1)αB .(1,cos )αC .(sin ,cos )ααD .(cos ,sin )αα9.在ABC 中,330,tan ,232A B AC ∠=== ,求AB 的长.10.如图,在Rt ABC 中,90C ∠= ,23,6AC BC ==,解这个直角三角形.六、当堂检测1.在ABC 中,30,1,3,2B AC BC AB ∠==== ,则A ∠为( )A .60B .45C .30D .无法求A ∠2.如图所示是教学用直角三角板,边330,90,tan 3AC cm C BAC =∠=∠= ,则边BC 的长为( ) A . 303cm B .203cm C .103cm D .53cm3.如图所示,在等腰Rt ABC 中,若90C ∠= ,6,AC D =是AC 上一点,若1tan 5DBA ∠=,则AD 长为( ) A .2 B .3 C .2 D .1第6题图4.如图所示,在梯形ABCD 中,458AD BC B AB ∠=∠= ∥,,C=120,,则CD 的长为( )A .863B .46C .823D .42 5.如图所示,两条宽度为1的纸条相交成α角,那么重叠部分(阴影部分)的面积是( ) A .1 B .1sin α C .21cos α D .1cos α6. 在等腰ABC 中,一腰上的高线长为3,这条高与另一腰的夹角为30 ,则ABC 的面积为 .7.如图所示,在Rt ABC 中,90C ∠= ,8AC =,A ∠的平分线1633AD =,则BC = . 8.时代中学计划在如图所示的一块三角形空地上种植草皮,已知1502030A AB m AC m ∠=== ,,,每平方米草皮的售价为a 元.购买这种草皮至少需要多少元?第5题 第7题 第3题 第4题。

初中数学青岛版九年级上册高效课堂资料课题 解直角三角形的复习教学目标知识与能力 1、理解锐角三角函数的概念,并能够通过实例进行说明。
2、记住特殊角的三角函数值,并会计算。
3、能够运用三角函数解直角三角形,并解决与直角三角形有关的实际问题过程与方法 培养学生分析问题和解决问题的能力情感态度价值观 通过复习能系统地掌握本章知识重点难点理解锐角三角函数的概念,并能够通过实例进行说明。
记住特殊角的三角函数值,并会计算。
课前预习案1.锐角三角比定义。
在直角三角形ABC 中,∠C=90°,设BC=a ,CA=b ,AB=c ,锐角A 的三个三角比是: sin A = c a , cos A = c b , tan A =ba 2.互余两角三角函数间的关系:sin α=cos(900-α) cos α=sin(900-α)3.特殊角的三角比值:300 450 60°4.锐角三角比的增减性正弦函数和正切函数是增函数;余弦函数比是减函数。
5.锐角三角比值的范围:0<sin α<1,0<cos α<1,tan α>0课内探究案自学导航 1.Rt△ABC 中,∠C=90°,∠B=60°,两直角边的和为14,求这个直角三角形的面积。
2.,AC⊥BC,cos∠ADC=,∠B=30°AD=10,求 BD 的长。
指导生互动交流,解决生自学中的困惑问题点评:1、实际问题转化实际问题。
2、作辅助线的方法。
学以致用: 1.在△ABC 中,∠C=90°,AC =2.1cm ,BC =2.8cm 。
求:(1)△ABC 的面积; (2)斜边的长;(3)高CD.2.Rt△ABC中,∠C=90°,AC=8,∠A的平分线AD=,求∠B的度数以及边BC、AB 的长。
变式拓展如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)课堂小结学生回顾浅谈收获课内达标题(总分10分得分-----)4、sin45°+sin60°-2cos45°;。

解直角三角形总结解直角三角形与直角三角形的概念、性质、判定和作图有着密切的联系,是在深入研究几何图形性质的基础上,根据已知条件,计算直角三角形未知的边长、角度和面积,以及与之相关的几何图形的数量。
1、明确解直角三角形的依据和思路在直角三角形中,我们是用三条边的比来表述锐角三角函数定义的.因此,锐角三角函数的定义本质揭示了直角三角形中边角之间的关系,是解直角三角形的基础。
如图1,在Rt△ABC中,∠C=90°,设三个内角A、B、C所对的边分别为a、b、c(以下字母同),则解直角三角形的主要依据是(1)边角之间的关系:sinA=cosB=ac, cosA=sinB=bc,tanA=cotB=ab,cotA=tanB=ba。
(2)两锐角之间的关系:A+B=90°。
(3)三条边之间的关系:。
以上每个边角关系式都可看作方程,解直角三角形的思路,就是根据已知条件,正确地选择直角三角形中边角间的关系式,通过解一元方程来求解。
2、解直角三角形的基本类型和方法我们知道,由直角三角形中已知的元素求出未知元素的过程叫作解直角三角形,而在直角三角形中,除直角以外还有三条边及两个锐角共五个元素,那么什么样的直角三角形才可解呢?如果已知两个锐角能否解直角三角形呢?事实上,解直角三角形跟直角三角形的判定与作图有着本质的联系,因为已知两个元素(至少有一个是边)可以判定直角三角形全等,也可以作出直角三角形,即此时直角三角形是确定的,所以这样的直角三角形是可解的。
由于已知两个锐角的直角三角形是不确定的,它们是无数多个相似的直角三角形,因此求不出各边的长。
所以,要解直角三角形,给出的除直角外的两个元素中,必须至少有一个是边。
这样,解直角三角形就分为两大类,即已知一条边及一个锐角或已知两条边解直角三角形。
四种基本类型和解法列表如下:已知条件解法一边及一锐角直角边a及锐角A B=90°-A,b=a·tanA,c=sinaA斜边c及锐角A B=90°—A,a=c·sinA,b=c·cosA两边两条直角边a和b ,B=90°—A,直角边a和斜边c sinA=ac,B=90°-A,例1、如图2,若图中所有的三角形都是直角三角形,且∠A=α,AE=1,求AB的长。

初中数学青岛版九年级上册高效课堂资料 No.62《 解直角三角形》复习探究案班级_____小组_______姓名_________评价_________【核心素养】数学运算、数学建模 【探究目标】自主构建,能绘制出三角形的知识体系,并能说出解直角三角形的三个类型,会运用三角模型解决生活中的直角求解问题,用自己的话说出建模思想的两点体会。
【使用说明】复习探究九上课本P 38-P 59的基础知识,完成学案。
【自我提升】1.在直角三角形ABC 中,∠C=90°,b=1,tanA=3,则c 的长为( )A . 2B . 5C .22D .102.如果|3tan 3|5.0cos -+-B A =0,那么△ABC 是( )A. 锐角三角形B. 直角三角形C. 等边三角形D. 钝角三角形 3. 如图,A 、B 、C 三点在正方形网格线的交点处,若将△ACB 绕着点A 逆时针旋转得到△A 'C 'B ',则tanB '的值为( )A .12 B .13C .14 D4.在Rt △ABC 中,∠ACB=90°,CD ⊥AB ,则下列等式一定不成立的是( )A .AC 2=AD •AB B .BC 2=BD •ABC .AB 2=AC •BCD .CD 2=AD •BD5.已知等腰三角形两条边的长分别是3,7,底角为α,则cos α= 6.在△ABC 中,若AB=5,BC=13,AD 是BC 边上的高,AD=4,则tanC= .7.如图,为测量某物体AB 的高度,在D 点测得A 点的仰角为30°,朝物体AB 方向前进20米,到1020米再 沿北偏西30°方向走了若干千米到达C 地,测得A 地在C 地南偏西30°方向,则A 、C 两地的距离为。
第7题 第8题 第9题 第10题9.如图小明想测量电线杆AB 的高度,发现电线杆的影子恰好落在土坡的坡面CD 和地面BC 上,量得CD=4 m ,BC=10 m ,CD 与地面成30°角,且此时测得 1 m 杆的影子长为 2 m ,则电线杆的高度约为 __________m .(结果保留根号) 10.如图,在2×2的网格中,以顶点O 为圆心,以2个单位长度为半径作圆弧,交图中格线于点A ,则tan ∠ABO 的值为( ) A .B .2C .D .311.如图,以圆O 为圆心,半径为1的弧交坐标轴于A ,B 两点,P 是上一点(不与A ,B 重合),连接OP ,设∠POB=α,则点P 的坐标是( )A .(sin α,sin α)B .(cos α,cos α)C .(cos α,sin α)D .(sin α,cos α)12.如图,如果在坡度i=1:2.4 的斜坡上两棵树间的水平距离AC 为3米,那么两树间的坡面距离AB 是 米.13.小刚在一山坡上依次插了三根木杆,第一根木杆与第二根木杆插在倾斜角为30°,且坡面距离是6米的坡面上,而第二根与第三根又在倾斜角为45°,且坡面距离是8米的坡面上.则第一根与第三根木杆的水平距离是 米.(如图)(结果保留根号)第11题 第12题 第13题 14.如图,为测量一座山峰CF 的高度,将此山的某侧山坡划分为AB 和BC 两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°. (1)求AB 段山坡的高度EF ; (2)求山峰的高度CF .( 1.414,CF 结果精确到米)15.如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方2米处的点C出发,沿斜面坡度i=1:的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈,cos37°≈,tan37°≈.计算结果保留根号)16.一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)17.如图,大楼底右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上).已知AB=80m,DE=10m,求障碍物B,C两点间的距离.(结果保留根号)18.某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:.(1)求新坡面的坡角a;(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.。

初三数学:《解直角三角形》知识点总结知识点在不断更新的同时也需要及时的归纳总结,才能更好的掌握,接下来精品学习网初中频道给大家整理解直角三角形知识点整理,供大家参考阅读。
1解直角三角形一、锐角三角函数(一)、锐角三角函数定义在直角三角形ABC中,∠C=900,设BC=a,CA=b,AB=c,锐角A的四个三角函数是:(1)正弦定义:在直角三角形中ABC,锐角A的对边与斜边的比叫做角A的正弦,记作sinA,即sin A=ca,(2)余弦的定义:在直角三角行ABC,锐角A的邻边与斜边的比叫做角A的余弦,记作cosA,即cos A=cb,(3)正切的定义:在直角三角形ABC中,锐角A的对边与邻边的比叫做角A的正切,记作tanA,即tan A=ba,(4)锐角A的邻边与对边的比叫做∠A的余切,记作cotA 即aAAAb的对边的邻边cot 锐角A的正弦、余弦,正切、余切都叫做角A的锐角三角函数。
这种对锐角三角函数的定义方法,有两个前提条件:(1)锐角∠A必须在直角三角形中,且∠C=900;(2)在直角三角形ABC中,每条边均用所对角的相应的小写字母表示。
否则,不存在上述关系2注意:锐角三角函数的定义应明确(1)ca,cb,ba,ab四个比值的大小同△ABC的三边的大小无关,只与锐角的大小有关,即当锐角A取固定值时,它的四个三角函数也是固定的;(2)sinA不是sinA的乘积,它是一个比值,是三角函数记号,是一个整体,其他三个三角函数记号也是一样;(3)利用三角函数定义可推导出三角函数的性质,如同角三角函数关系,互余两角的三角函数关系、特殊角的三角函数值等;(二)、同角三角函数的关系(1)平方关系:122sin=∂+COSα(2)倒数关系:tana cota=1(3)商数关系:∂∂=∂∂∂=sincoscot,cossintan注意:(1)这些关系式都是恒等式,正反均可运用,同事还要注意它们的变形公式。
(2)()∂∂sinsin22是的简写,读作“∂sin的平方”,不能将∂∂22sin写成sin前者是a的正弦值的平方,后者无意义;(3)这里应充分理解“同角”二字,上述关系式成立的前提是所涉及的角必须相同,如1cottan,1223030cossin22=•=∂+∂οο,而1cossin22=+∂β就不一定成立。
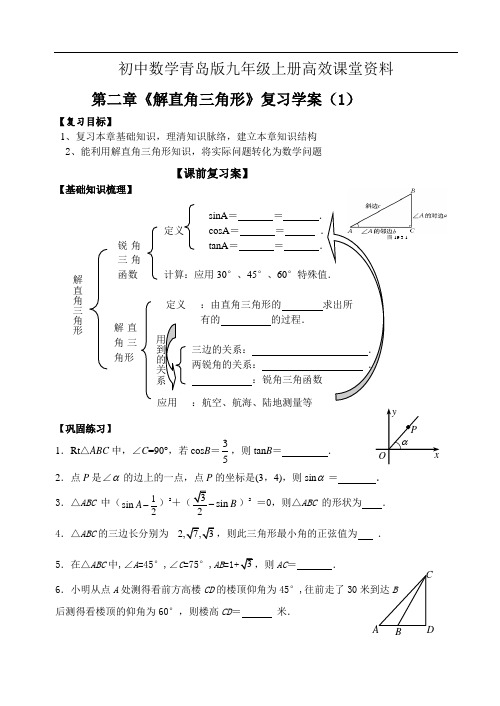
图19.3.1 初中数学青岛版九年级上册高效课堂资料第二章《解直角三角形》复习学案(1)【复习目标】1、复习本章基础知识,理清知识脉络,建立本章知识结构2、能利用解直角三角形知识,将实际问题转化为数学问题【课前复习案】 【基础知识梳理】【巩固练习】1.Rt △ABC 中,∠C =90°,若cos B =35,则tan B = . 2.点P 是∠α的边上的一点,点P 的坐标是(3,4),则sin α= .3.△ABC 中(1sin 2A -)2+(3sin 2B -)2 =0,则△ABC 的形状为 . 4.△ABC 的三边长分别为2,7,3,则此三角形最小角的正弦值为 .5.在△ABC 中,∠A =45°,∠C =75°,AB =1+3,则AC = .6.小明从点A 处测得看前方高楼CD 的楼顶仰角为45°,往前走了30米到达B后测得看楼顶的仰角为60°,则楼高CD = 米. 解直角三角形 定义 计算:应用30°、45°、60°特殊值. 锐角三角函数 解直角三角形 sinA = = .cosA = = .tanA = = . 定义 应用 :由直角三角形的 求出所有的 的过程.三边的关系: .两锐角的关系: .:锐角三角函数用到的关系:航空、航海、陆地测量等 A CB Dxy O P α【课内探究案】一、1课内探究(取人之长,补己之短)例1、在△ABC 中,∠A =30°,∠ACB =135° ,AC =20,求△ABC 的面积.例2、如图,某船向正东方向航行,在A 处望见某岛C 处在北偏东60º方向,前进6海里到达B 点,望见C 在北偏东30º方向,并测得该岛周围6海里内有暗礁,若该船继续向东航行,有无暗礁危险?是说明理由。
北CA B 东变式:一艘渔船在海中自西向东航行,速度为28海里/小时,船在A 处测得灯塔C 在北偏东60°方向,半小时后渔船到达B 点,测得灯塔C 在北偏东15°方向,求船与灯塔间的最近距离.【达标测试】(演练巩固,自我检测)要求独立完成课本检测站(10分钟)自我检测本章掌握情况完成后教师出示答案学生自我核对。
二、课内探究(2)解答过程的思路:实际问题解直角三角形问题1、创设问题情景,引出新知:上海东方明珠塔于1994 年10 月1 日建成,出示图片,在各国广播电视塔的排名榜中,当时其高度列亚洲第一、世界第三.与外滩的“万国建筑博览群”隔江相望.在塔顶俯瞰上海风景,美不胜收.运用本章所学过的知识,能测出东方明珠塔的高度来吗?思考回答转化问题答案求出有关的边或角AB ECDA CDB四、思维扩展,举一反三五、巩固提高3、根据已知条件和所学知识,这种形状的图形能不能解?仿照例1根据下图和图中的已知,编写一道应用“解直角三角形”知识的题。
(要求叙述完整)例2、如图,河对岸有水塔AB 。
在C 处测得塔顶A的仰角为30°,向塔前进12m 到达D ,在D 处测得A 的仰角为45°, 求塔高。
通过编写题目来加深学生对解直角三角形应用的理解与掌握,达到扩散思维的作用1、积极思考,踊跃回答,并计算结果。
2、四人小组讨论,给出结果。
450 3006米(自主探究,合作学习,采用小组合作的方法)教学程序教师活动学生活动一、学前准备二、自学探究1.指南或指北的方向与目标方向线构成小于900的角,叫做__ ____,如图:点A在点O的___________,点B在点O的南偏西45º或方向.2阅读课本80页中有关坡度的内容,说一说什么是坡角,什么是坡度或坡比,坡度与坡角的正切有什么关系? 请把重点知识写在下面.______________________________________________________________________________1、某地计划在河流的上游修建一条拦水大坝,大坝的横断面ABCD是梯形(如图),坝顶宽BC=6米,坝高25米,应水坡AB的坡度i=1:3,被水坡CD的坡度i=1:2.5.(1).求斜坡AB和CD的长(精确到0.01米);(2).求拦水大坝的底面AD的宽.做一做,看谁做得快组内探索,交流推荐学生回答BC10米A D E5.6米i=1:2.5α β三、练习自测1.一名滑雪运动员从坡度为1:5的山坡上滑下,如果这名运动员滑行的距离为150米,那么他下降的高度是多少(精确到0.1米)?2.如上图,拦水坝的横断面为梯形ABCD ,根据图中数据,求:(1).角α和β的大小(精确到1 ) (2)、坝底宽AD 和斜坡AB 的长(精确到0.1米) 3.入夏以来,松花江哈尔滨段水位不断下降,达到历史最低水位,一条船在松花江某水段自西向东沿直线航行,在A 处测得航标C 在北偏东60°方向上,前进100米到达B 处,又测得航标C 在北偏东45°方向上,如图9,在以航标C 为圆心,120米长为半径的圆形区域内有浅滩,如果这条船继续前进,是否有被浅滩阻碍的危险?A 、B 两市相距100公里,在A 市东偏北30º方向,B 市的西北方向是一森林公园C ,方圆30公里.若在思考回答、推举同学讲解先独立解答,不会的相互帮助 所思所想四、拓展延伸五、归纳小结A、B两市间修一条笔直的高速公路.它会不会穿过森林公园.1.这节课我的收获和疑问:___________________________我将____________________________________________________ ______解决我的困惑。
青岛版数学九年级上册《解直角三角形的典型例题的解析》教学设计1一. 教材分析《解直角三角形的典型例题的解析》是青岛版数学九年级上册中的一部分内容。
这部分内容主要让学生掌握解直角三角形的原理和方法,能够运用到实际问题中。
教材通过典型的例题,引导学生掌握解题技巧和方法,培养学生的逻辑思维能力和解决问题的能力。
二. 学情分析学生在学习这部分内容前,已经掌握了相似三角形的性质和解三角形的知识。
他们对解三角形的方法有一定的了解,但解直角三角形涉及到更多的计算和逻辑推理,对学生来说是一个较大的挑战。
因此,在教学过程中,需要引导学生逐步理解解直角三角形的原理,并通过大量的练习来巩固知识。
三. 教学目标1.知识与技能目标:让学生掌握解直角三角形的原理和方法,能够运用到实际问题中。
2.过程与方法目标:通过典型的例题,引导学生掌握解题技巧和方法,培养学生的逻辑思维能力和解决问题的能力。
3.情感态度与价值观目标:激发学生对数学的兴趣,培养他们积极思考和合作探究的学习态度。
四. 教学重难点1.重点:解直角三角形的原理和方法。
2.难点:解直角三角形的计算和逻辑推理。
五. 教学方法1.引导法:通过问题引导学生思考,让学生自主探索解直角三角形的方法。
2.示范法:教师通过讲解典型的例题,展示解题的步骤和方法。
3.练习法:学生通过大量的练习,巩固解直角三角形的知识。
六. 教学准备1.准备相应的教学PPT,展示例题和解题过程。
2.准备一些实际问题,用于巩固和拓展学生的知识。
七. 教学过程1.导入(5分钟)通过一个实际问题,引导学生思考解直角三角形的方法。
例如,给出一个直角三角形,已知两个直角边的长度,让学生求斜边的长度。
2.呈现(15分钟)教师通过PPT展示典型的例题,并讲解解题的步骤和方法。
例如,给出一个直角三角形,已知两个直角边的长度,让学生求斜边的长度。
教师讲解如何使用勾股定理进行计算。
3.操练(15分钟)学生独立完成一些类似的练习题,巩固解直角三角形的知识。
青岛版数学九年级上册《解直角三角形》说课稿2一. 教材分析青岛版数学九年级上册《解直角三角形》是本册教材中的一个重要内容。
本节课的内容包括了解直角三角形的性质,学会使用勾股定理,掌握解直角三角形的方法。
这部分内容在数学学习中占有重要的地位,它不仅巩固了之前学习的几何知识,而且为后续学习解析几何、三角函数等知识打下了基础。
二. 学情分析九年级的学生已经掌握了基本的代数和几何知识,具备了一定的逻辑思维能力和问题解决能力。
但是,对于解直角三角形的理解和应用,部分学生可能会感到困难,特别是对于勾股定理的理解和运用。
因此,在教学过程中,我们需要关注这部分学生的学习情况,帮助他们理解和掌握解直角三角形的方法。
三. 说教学目标1.知识与技能目标:学生能够了解直角三角形的性质,掌握解直角三角形的方法,学会使用勾股定理。
2.过程与方法目标:通过观察、操作、思考、交流等活动,培养学生的空间观念和几何思维能力。
3.情感态度与价值观目标:激发学生对数学的兴趣,培养学生的团队合作意识和问题解决能力。
四. 说教学重难点1.教学重点:学生能够掌握解直角三角形的方法,学会使用勾股定理。
2.教学难点:学生对于勾股定理的理解和运用,以及对于解直角三角形方法的灵活运用。
五. 说教学方法与手段1.教学方法:采用问题驱动法、合作学习法、引导发现法等教学方法,引导学生主动探究、合作交流,培养学生的几何思维能力。
2.教学手段:利用多媒体课件、几何模型等教学手段,帮助学生直观地理解直角三角形的性质和解直角三角形的方法。
六. 说教学过程1.导入:通过一个实际问题,引出直角三角形的概念,激发学生的兴趣。
2.探究:引导学生通过观察、操作、思考等活动,发现直角三角形的性质和解直角三角形的方法。
3.讲解:讲解勾股定理的含义和运用,解释解直角三角形的方法。
4.练习:学生进行相关的练习,巩固所学知识。
5.拓展:引导学生思考直角三角形在实际生活中的应用,激发学生的学习兴趣。
专题一 锐角三角函数本专题包括两个方面的知识点,一是锐角三角函数的概念,二是一般的锐角三角函数值的计算.这两个知识点是本章的基础,也是解决实际问题的关键,通过本专题的复习应达到以下目标:(1)掌握锐角三角函数定义;(2)掌握锐角三角函数值的几种不同的计算方法.例1 三角形在正方形网格纸中的位置如图1所示,则sin α的值是( ).A .34B .43C .35D .45分析:本题是一道设计比较新颖的试题,它通过网格的特征给出解题信息,由正方形网格可知角α的对边的长为3,邻边的长为4,要求sin α,只要根据勾股定理求出三角形的斜边,再根据三角函数的定义计算即可.解:设α的对边为a ,邻边为b ,斜边为c ,则a =3,b =4,所以5c =,所以3sin 5a c α==,选C . 说明:解决这类问题的思路是依据图形确定三角形的三边的长,然后根据定义进行计算.例2 如图2,△ABC 中,△C =90°,AC +BC =7(AC >BC ),AB =5,则tan B=______. 分析:要求tan B ,根据锐角三角函数的定义,则需要求对边AC 和邻边BC 的长,因为知道斜边AB =5,且AC +BC =7,所以可以根据勾股定理进行计算.解:设AC =x ,则BC =7-x ,根据勾股定理,得222(7)5x x +-=,解得4x =.所以43AC BC ==,.所以4tan 3AC B BC ==. 说明:本题的解题思路是根据已知条件确定△B 的对边和邻边的长,采用了一般的解题方法,并体现了方程思想在求三角函数值中的应用.实际上,本题是一道填空题,不通过计算直接观察就可以解决.因为斜边是5,且两条直角边的和为7,所以两条直角边的长分别是4和3.例3 在Rt△ABC中,△C=90°,若AB=2AC,则cos A的值等于().A.3B.32C.12D.33分析:已知三角形的两边的关系,要求cos A,根据三角函数的定义可知,cosACAAB=,所以只要由已知条件求出ACAB即可.解:因为2AB AC=,所以12ACAB=.所以1cos2ACAAB==.选C.说明:本题是一道选择题,解决问题时可以采用取特殊值的方法,即令AC=1,则AB=2.这样更简单.专题训练:1.在△ABC中,△C=90°,AB=2,AC=1,则sin B的值是().A.12B.22C.32D.22.在△ABC中,△C=90°,22sin3BC A==,,则边AC的长是().A.5B.3C.43D.133.如图3,在Rt△ABC中,△ACB=90°,CD△AB,垂足为D.已知AC=5,BC=2,那么sin△ACD=().A.53B.23C.255D.52参考答案:1.A 2.A 3.A。