直线及圆的参数方程

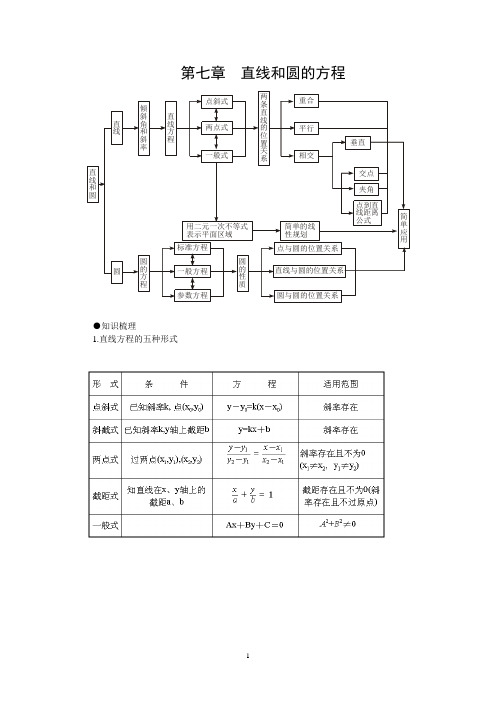
第七章直线和圆的方程●知识梳理1.直线方程的五种形式2.直线的倾斜角、斜率及直线的方向向量及位置关系:（1）直线的倾斜角在平面直角坐标系中，对于一条与x 轴相交的直线，如果把x 轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为α，那么α就叫做直线的倾斜角.直线和x 轴平行或重合时，直线的倾斜角为0°,直线倾斜角取值范围0°≤α＜180°. （2）直线的斜率倾斜角α不是90°的直线，它的倾斜角的正切叫做这条直线的斜率，常用k 表示，即k =tan α（α≠90°）.倾斜角是90°的直线没有斜率；倾斜角不是90°的直线都有斜率，其取值范围是（－∞，+∞）.（4）求直线斜率的方法①定义法：已知直线的倾斜角为α，且α≠90°，则斜率k =tan α.②公式法：已知直线过两点P 1（x 1，y 1）、P 2（x 2，y 2），且x 1≠x 2，则斜率k =1212x x y y --.平面直角坐标系内，每一条直线都有倾斜角，但不是每一条直线都有斜率. 对于直线上任意两点P 1（x 1，y 1）、P 2（x 2，y 2），当x 1=x 2时，直线斜率k 不存在，倾斜角α=90°；当x 1≠x 2时，直线斜率存在，是一实数，并且k ≥0时，α=arctan k ，k ＜0时，α=π+arctan k .（5）到角与夹角：若直线l 1, l 2的斜率分别为k 1, k 2，将l 1绕它们的交点逆时针旋转到与l 2重合所转过的最小正角叫l 1到l 2的角；l 1与l 2所成的角中不超过900的正角叫两者的夹角。

若记到角为θ，夹角为α，则tan θ=21121k k k k +-,tan α=21121k k k k +-.（6）平行与垂直：若直线l 1与l 2的斜率分别为k 1, k 2。

且两者不重合，则l 1//l 2的充要条件是k 1=k 2；l 1⊥l 2的充要条件是k 1k 2=-1。

第一讲 求直线和圆的方程方法总结※求直线方程的若干方法：直线是数学中最常见的图形,直线方程数学中最常用方程,该知识点与其他知识点的融合是最紧密的,考查的题型和方法也多样，这里总结复习几种不同的求直线方程的方法. 【关健词】直线方程 方法 一、知识要点概述:1、直线的方程、方程的直线概念；2、直线方程形式（1）点斜式：直线过点00(,)x y 斜率为k ，直线方程：00()y y k x x -=-,它不包括垂直于x 轴直线； （2）斜截式：直线在y 轴上的截距为b 和斜率k ，直线方程：y kx b =+,它不包括垂直于x 轴直线； （3）两点式：直线经过111(,)P x y 、222(,)P x y 两点，直线方程：121121x x x x y y y y --=--，它不包括垂直于坐标轴的直线；（4）截距式：直线在x 轴和y 轴上的截距为,a b ,直线方程：1=+bya x ，它不包括垂直于坐标轴的直线和过原点的直线；（5）一般式：任何直线均可写成0Ax By C ++=(A ,B 不同时为0)的形式. 提醒：(1)直线方程的各种形式都有局限性.（如点斜式不适用于斜率不存在的直线，还有截距式呢？）；(2)直线在坐标轴上的截距可正、可负、也可为0.直线两截距相等⇔直线的斜率为-1或直线过原点；直线两截距互为相反数⇔直线的斜率为1或直线过原点； 直线两截距绝对值相等⇔直线的斜率为1±或直线过原点.如过点(1,4)A ，且纵横截距的绝对值相等的直线共有___条（答：3） 二、解题方法指导:1、求直线方程的基本思想和方法是恰当选择方程的形式，利用待定系数法求解直接写出直线方程 设直线方程的一些常用技巧：（1）知直线纵截距b ，常设其方程为y kx b =+；（2）知直线横截距0x ，常设其方程为0x my x =+(它不适用于斜率为0的直线)；（3）知直线过点00(,)x y ，当斜率k 存在时，常设其方程为00()y k x x y =-+，当斜率k 不存在时，则其方程为0x x =；（4）与直线:0l Ax By C ++=平行的直线可表示为10Ax By C ++=； （5）与直线:0l Ax By C ++=垂直的直线可表示为10Bx Ay C -+=.（6）经过两条直线0111=++C y B x A 和0222=++C y B x A 的交点的直线系方程为：λ+++111C y B x A 0)(222=++C y B x A （λ为参数）.2、具体方法有：⑴利用公式求直线方程；⑵通过直线系求直线方程；⑶借助相关点求直线方程——轨迹法； ⑷利用参数求直线方程；⑸通过分析结构求直线方程. 三、范例剖析 1、直接法例1、直线l 在y 轴上的截距为3，且倾斜角α的正弦值为45，求直线l 的方程.解：4sin 5α=，3cos 5α=±，∴直线的斜率43k =±故所求直线的方程为433y x =±+，即4390x y -+=或4390x y +-= 评注：由题意直接选择直线方程五种形式中的任何一个，写出形式适当的方程即为直接法.同时，求解本例时不要混淆概念，倾斜角应在[0,)π内，从而cos α有两个解. 2、待定系数法（公式法）例2、过点P (2，1）作直线l 交y x ,正半轴于AB 两点，当||||PB PA ⋅取到最小值时，求直线l 的方程.解法1：设直线l 的方程为：)0(),2(1≠-=-k x k y令y ＝0解得kx 12-=；令x ＝0，解得k y 21-=，∴A （k 12-，0），B （0，k 21-），∴||||PB PA ⋅＝)4)(11(22k k ++4248)1(4822=⨯+≥++=kk当且仅当12=k 即1±=k 时，||||PB PA ⋅取到最小值.又根据题意0<k ，∴1-=k 所以直线l 的方程为：03=-+y x方法2：由题设，可令直线l 为：1(2)y k x -=-，分别令y =0和x =0 可得21(,0)k A k-，B （0，1-2k ）.∴2221||||1(2)4(121)k PA PB k k-⋅=+-+-- 442)2(2)1(22222222==≥+=k k k k k k当且仅当12=k 即1k =±时，||PA PB ⋅取最小值4.又0k >∴k =-1，这时直线l 的方程是x +y -3=0.方法3：设直线l 方程为1=+b y a x ，l 过（2，1）点∴112=+b a ∴2-=a ab∴22||||(2)14(1)PA PB a b ⋅=-++-8)2(4)2(428)2(4)2(42222+--≥+-+-=a a a a 488=+=（以下略）.评述：此题在求解过程中运用了基本不等式，同时应注意结合直线与坐标轴正半轴相交而排除k ＝1的情形.引申1：过点P （2，1）作直线l 交x 轴、y 轴正方向于A 、B ，求使∆A O B 的面积最小时的直线l 的方程.yBP(2,1)O A解：设所求直线方程为x a y b +=1，则由直线l 过点P （2，1），得21100a ba b +=>>()，即b aa =-2，由b >0，得a >2， 所以S a b a a a A O B∆==⋅-12122221442(2)22a a a a -+==⋅--14(2)22a a =++- 14[(2)4]22a a =-++-14]42≥= 当且仅当a a -=-242，即a b ==42，时，S AOB ∆取得最小值为4 此时所求直线方程为x y421+=，即x y +-=240 评注：由题意直接选择直线方程五种形式中最恰当的一种形式来假设方程，再求解方程，称为公式法.这里选择了截距式方程.引申2：在本例条件下，求求直线l 在两坐标轴截距之和的最小值及其此时直线l 的方程. （参考数学试题精编P 54） 3、直线系法：直线系的定义：具有某种共同性质的直线的集合，叫做直线系．它的方程叫做直线系方程.例3. 求过02321=+-y x l ：与l x y 23420：--=交点且与直线440x y +-=平行的直线方程. 解：设l 1与l 2交点的直线方程为：(*)0)243()232(=--++-y x y x λ即022)43()32(=-+--++λλλy x 因为所求直线与044=-+y x 平行，所以143432λλ--=+，解得λ=-1419 将λ=-1419代入(*)，得:所求直线方程为4660x y +-= 4、相关点法:利用相关点法求直线的方程实质上是轨迹法.例4、 求直线l x y '：--=20关于直线l x y ：330-+=的对称直线方程. 解：设所求的对称直线上任意一点坐标为（x ，y ）关于直线l 的对称点为()x y 00，，则⎪⎪⎩⎪⎪⎨⎧-=⋅--=++-+⋅13032230000x x yy y y x x ，解得⎪⎪⎩⎪⎪⎨⎧++=-+-=53545359535400y x y y x x ，因为()x y 00，在直线x y --=20上 所以x y 0020--=，()()-+--++-=45359535453520x y x y ，即7220x y ++=5、参数法例5、直线l 经过M （0，1），且被直线1l ：x -3y +10=0和2l ：2x +y -8=0所截得的线段恰以M 为中点，求直线l 的方程．解法1.：过点M 且与x 轴垂直的直线显然不合题意，故可设所求直线方程为y =kx +1,与已知直线1l ，2l 交于A ，B 两点，联立方程组：{{()11()3100280y kx y kx I II x y x y =+=+-+=+-=，由（I ）解得A x =731k -，由（II ）解得B x =72k +，点A 平分线段AB ， 2A B M x x x ∴+=即：731k -+72k +=0，解得14k =-，故所求直线的方程为：x +4y -4=0.解法2：设l 交1l 于A （3t -10，t ），l 交2l 于B （u ，8－2u ），利用中点坐标公式得： ∴31002822t u t t u -+=⎧⇒=⎨+-=⎩ , ∴A （-4，2） 由直线方程的两点式可得，直线l 的方程为：102140y x --=---，即x +4y -4=0. 解法3：设l 与已知直线1l ，2l 交于A ，B 两点，点 A （3t -10，t ）在直线1l 上，则由中点坐标公式得A 关于M （0，1）的对称点B （10-3t ，2- t ），点B 在直线2l 上，∴2(103)(2)802t t t -+--=⇒=， 以下同解法2，此处略. 解法4. 设所求直线方程为y =kx +1,代入方程（x -3y +10）·（ 2x +y -8）=0得：()()22253287490k k x k --++-=，同解法1设所求直线与已知直线1l ，2l交于A ，B 两点，由题意：2287253A B k x x k k++=---=2M x =0，可得：14k =-，故所求直线的方程为：x +4y -4=0. 注意：本题所求直线过点M （0，1），故只要设出直线方程的点斜式，由题中另一条件即可确定斜率，思路顺理成章.但是想在解题过程中不断地提高自己的逻辑思维能力以及分析问题，解决问题的能力，还应联系题中已知条件和相关知识，看能否找到新的解法，如解法2，解法3，而解法4在学习了后续知识后会有更深刻的体会. 6、结构分析法：例6、已知两直线l 1:a 1x +b 1y +1=0和l 2：a 2x +b 2y +1=0的交点为P （2，3），求过两点Q 1（a 1，b 1）、Q 2（a 2，b 2）（a 1≠a 2）的直线方程.分析：利用点斜式或直线与方程的概念进行解答.解：∵P （2，3）在已知直线上，2a 1+3b 1+1=0，2a 2+3b 2+1=0.∴2（a 1－a 2）+3（b 1－b 2）=0，即2121a a b b --=－32.∴所求直线方程为y －b 1=－32（x －a 1），∴2x +3y －（2a 1+3b 1）=0，即2x +3y +1=0. 评述：此解法运用了整体代入的思想，方法巧妙.解法2：将l 1与l 2的交点P （2，3）代入l 1与l 2的方程，得11222310,230a b a b ++=+=，根据以上两式的结构特点易知：点与Ba b ()22，的坐标都适合方程2x +3y +1=0故经过点A 、B 的直线l 的方程为x y +=23练习：若两条直线33222111=+=+y b x a l y b x a l ：，：相交于点P （1，2），试求经过点Aa b ()11，与)(22b a B ，的直线方程.解：将l 1与l 2的交点P （1，2）代入l 1与l 2的方程，得3211=+b a ，a b 2223+=根据以上两式的结构特点易知：点与Ba b ()22，的坐标都适合方程xy +=23 故经过点A 、B 的直线l 的方程为x y +=23巩固练习：1、过点P （3，0）作一直线，使它夹在两直线l x y 1220：--=和l x y 230：++=之间的线段AB 恰被P 点平分，求此直线方程.解：设所求直线分别与l l 12、交于A 、B ，因为A 在l 1直线上，故可设A t t ()，22- 又P （3，0）为AB 的中点，由中点坐标公式，得B t t ()622--， 由B 在l 2上，得03)22()6(=+-+-t t ，解得，即A ()113163， 由两点式得所求直线方程为0248=--y x .2、一直线被两直线1l ：064=++y x ，2l ：0653=--y x 截得的线段的中点恰好是坐标原点，求该直线方程.解：设所求直线与1l ，2l 的交点分别是A 、B ，设A (00,y x ），则B 点坐标为(00,y x --)因为A 、B 分别在1l ，2l 上，所以⎩⎨⎧=-+-=++06530640000y x y x ②①①＋②得：0600=+y x ，即点A 在直线06=+y x 上，又直线06=+y x 过原点，所以直线l 的方程为06=+y x .3、求过点P （2，3），并且在两轴上的截距相等的直线方程.解：在两轴上的截距都是0时符合题意，此时直线方程为3x －2y ＝0 若截距不为0，则设直线方程为ay a x +＝1 将点P （2，3）代入得aa 32+＝1，解得a ＝5 ∴直线方程为55yx +＝1，即x ＋y ＝5. 4、直线方程0=++C By Ax 的系数A 、B 、C 满足什么关系时，这条直线有以下性质? (1)与两条坐标轴都相交；(2)只与x 轴相交;(3)只与y 轴相交； (4)是x 轴所在直线；(5)是y 轴所在直线.答：(1)当A ≠0，B ≠0，直线与两条坐标轴都相交. (2)当A ≠0，B =0时，直线只与x 轴相交. (3)当A ＝0，B ≠0时，直线只与y 轴相交.(4)当A ＝0，B ≠0，C ＝0，直线是x 轴所在直线. (5)当A ≠0，B ＝0，C ＝0时，直线是y 轴所在直线.5、求与直线l ：5x -12y +6=0平行且到l 的距离为2的直线的方程.解：设所求直线的方程为5x -12y +c =0.在直线5x -12y +6=0上取一点P 0（0，21），点P 0到直线5x -12y +c =0的距离为：d =136)12(5211222-=-++⨯-c c ，由题意得136-c =2.所以c =32或c =-20.所以所求直线的方程为5x -12y +32=0和5x -12y -20=0. ※求圆方程的若干方法 一、知识要点总结： 1、圆的方程形式：⑴圆的标准方程：()()222x a y b r -+-=.⑵圆的一般方程：22220(40)x y Dx Ey F D E F ++++=>＋－， ⑶圆的参数方程：{cos sin x a r y b r θθ=+=+（θ为参数），其中圆心为(,)a b ，半径为r .圆的参数方程的主要应用是三角换元：222cos ,sin x y r x r y r θθ+=→==；22x y t +≤cos ,sin (0)x r y r r t θθ→==≤≤.⑷()()1122,,,A x y B x y 为直径端点的圆方程()()()()12120x x x x y y y y --+--= 2方法总结：求圆方程的主要方法是待定系数法，也经常数形结合来确定.例1、圆C 与圆22(1)1x y -+=关于直线y x =-对称，则圆C 的方程为____________ （答：22(1)1x y ++=）；例2、圆心在直线32=-y x 上，且与两坐标轴均相切的圆的标准方程是__________ （答：9)3()3(22=-+-y x 或1)1()1(22=++-y x ）；例3（以下各题参考数学精编p 63）求过两圆22(3)13x y ++=和22(3)37x y ++=交点，且圆心在直线y =x -4上的圆的方程.例4、求圆心在直线y =-2x 上，且与直线y =1-x 相切于点A （2，-1）的圆的方程.例5、圆心在直线y =2x -7上的圆C 与y 轴交于点A （0，-4），B （0，-2），求圆的方程.例6、半径为1的圆分别与y 轴正半轴和射线()30y x =≥相切，求圆的方程.例7、设圆方程满足：①截y轴所得弦长为2；②被x轴分成两段圆弧，其弧长之比为3:1；③圆心到直线l：x-2y=0，求该圆的方程.。

高二数学授课教案学生姓名授课教师班主任上课时间9 月 23 日时—时科目数学课题第1课时平面解析几何——直线与圆的方程学习目标1．回顾、加强空间坐标系、直线与圆的方程基础知识．2．巩固直线、圆的方程的主要求解方法．(重点)3．能够解决综合性解析几何问题．(难点)教学过程教学设计一、主干知识梳理1．直线方程的五种形式(1)点斜式：y－y1＝k(x－x1)(直线过点P1(x1，y1)，斜率为k，不包括y轴和平行于y轴的直线)．(2)斜截式：y＝kx＋b(b为直线l在y轴上的截距，且斜率为k，不包括y轴和平行于y轴的直线)．(3)两点式：y－y1y2－y1＝x－x1x2－x1(直线过点P1(x1，y1)，P2(x2，y2)，且x1≠x2，y1≠y2，不包括坐标轴和平行于坐标轴的直线)．(4)截距式：xa＋yb＝1(a、b分别为直线的横、纵截距，且a≠0，b≠0，不包括坐标轴、平行于坐标轴和过原点的直线)．(5)一般式：Ax＋By＋C＝0(其中A，B不同时为0)．设直线方程的一些常用技巧：1．知直线纵截距b，常设其方程为y kx b=+；2．知直线横截距x，常设其方程为x my x=+(它不适用于斜率为0的直线)；3．知直线过点00(,)x y，当斜率k存在时，常设其方程为00()y k x x y=-+，当斜率k不存在时，则其方程为x x=；4．与直线:0l Ax By C ++=平行的直线可表示为10Ax By C ++=； 5．与直线:0l Ax By C ++=垂直的直线可表示为10Bx Ay C -+=.提醒：求直线方程的基本思想和方法是恰当选择方程的形式，利用待定系数法求解。

2．直线的两种位置关系当不重合的两条直线l1和l2的斜率存在时： (1)两直线平行l1∥l2⇔k1＝k2. (2)两直线垂直l1⊥l2⇔k1•k2＝－1.提醒:当一条直线的斜率为0，另一条直线的斜率不存在时，两直线也垂直，此种情形易忽略．3．三种距离公式(1)A (x 1，y 1)，B (x 2，y 2)两点间的距离：|AB |＝ x 2－x 1 2＋ y 2－y 1 2. (2)点到直线的距离：d ＝|Ax 0＋By 0＋C |A 2＋B2(其中点P (x 0，y 0)，直线方程：Ax ＋By ＋C ＝0)．(3)两平行线间的距离：d ＝|C 2－C 1|A 2＋B 2(其中两平行线方程分别为l 1：Ax ＋By ＋C 1＝0，l 2：Ax ＋By ＋C 2＝0)．提醒:应用两平行线间距离公式时，注意两平行线方程中x ，y 的系数应对应相等．4．圆的方程的三种形式(1)圆的标准方程：(x －a )2＋(y －b )2＝r 2.(2)圆的一般方程：x 2＋y 2＋Dx ＋Ey ＋F ＝0(D 2＋E 2－4F >0)．(3)圆的参数方程：{cos sin x a r y b r θθ=+=+（θ为参数），其中圆心为(,)a b ，半径为r 。

直线与圆的方程一、概念理解：1、倾斜角：①找α：直线向上方向、x 轴正方向； ②平行：α=0°；③范围：0°≤α＜180° 。

2、斜率：①找k ：k=tan α （α≠90°）； ②垂直：斜率k 不存在； ③范围： 斜率 k ∈ R 。

3、斜率与坐标：12122121tan x x y y x x y y k --=--==α①构造直角三角形（数形结合）； ②斜率k 值于两点先后顺序无关； ③注意下标的位置对应。

4、直线与直线的位置关系：222111:,:b x k y l b x k y l +=+= ①相交：斜率21k k ≠（前提是斜率都存在）特例----垂直时：<1> 0211=⊥k k x l 不存在，则轴，即； <2> 斜率都存在时：121-=•k k 。

②平行：<1> 斜率都存在时：2121,b b k k ≠=； <2> 斜率都不存在时：两直线都与x 轴垂直。

③重合： 斜率都存在时：2121,b b k k ==； 二、方程与公式： 1、直线的五个方程：①点斜式：)(00x x k y y -=- 将已知点k y x 与斜率),(00直接带入即可； ②斜截式：b kx y += 将已知截距k b 与斜率),0(直接带入即可；③两点式：),(2121121121y y x x x x x x y y y y ≠≠--=--其中， 将已知两点),(),,(2211y x y x 直接带入即可；④截距式：1=+bya x 将已知截距坐标),0(),0,(b a 直接带入即可； ⑤一般式：0=++C By Ax ，其中A 、B 不同时为0 用得比较多的是点斜式、斜截式与一般式。

2、求两条直线的交点坐标：直接将两直线方程联立，解方程组即可3、距离公式：①两点间距离：22122121)()(y y x x P P -+-= ②点到直线距离：2200BA C By Ax d +++=③平行直线间距离：2221BA C C d +-=4、中点、三分点坐标公式：已知两点),(),,(2211y x B y x A①AB 中点),(00y x ：)2,2(2121y y x x ++ ②AB 三分点),(),,(2211t s t s ：)32,32(2121y y x x ++ 靠近A 的三分点坐标 )32,32(2121y y x x ++ 靠近B 的三分点坐标 中点坐标公式，在求对称点、第四章圆与方程中，经常用到。

§2 直线和圆锥曲线的参数方程2.1 直线的参数方程 2.2 圆的参数方程1.直线的参数方程(1)经过点P (x 0，y 0)、倾斜角是α的直线的参数方程为 ⎩⎨⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)① 其中M (x ，y )为直线上的任意一点，参数t 的几何意义是从点P 到M 的位移，可以用有向线段PM→的数量来表示. (2)经过两个定点Q (x 1，y 1)，P (x 2，y 2)(其中x 1≠x 2)的直线的参数方程为 ⎩⎪⎨⎪⎧x ＝x 1＋λx 21＋λ，y ＝y 1＋λy 21＋λ(λ为参数，λ≠－1). 其中M (x ，y )为直线上的任意一点，参数λ的几何意义是动点M 分有向线段QP →的数量比QM MP .当λ＞0时，M 为内分点；当λ＜0且λ≠－1时，M 为外分点； 当λ＝0时，点M 与Q 重合. 2.圆的参数方程(1)圆心在原点、半径为r 的圆的参数方程⎩⎨⎧x ＝r cos α，y ＝r sin α(α为参数).参数α的几何意义是OP 与x 轴正方向的夹角.(2)去掉圆与x 轴负半轴交点，圆心在原点、半径为r 的圆的参数方程.⎩⎪⎨⎪⎧x ＝（1－k 2）r 1＋k 2，y ＝2kr 1＋k 2(k 为参数)参数k 的几何意义是直线AP 的斜率.【思维导图】【知能要点】 1.直线的参数方程. 2.直线的参数方程的应用. 3.圆的参数方程及应用.题型一 直线的参数方程直线的参数方程⎩⎨⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α (α为参数)中，α，x 0，y 0都是常数，对于同一直线，选取的参数不同，会得到不同的参数方程.对于直线普通方程y ＝2x ＋1，如果令x ＝t ，可得到参数方程⎩⎨⎧x ＝t ，y ＝2t ＋1 (t 为参数)；如果令x ＝t2，可得到参数方程⎩⎪⎨⎪⎧x ＝t 2，y ＝t ＋1(t 为参数).这样的参数方程中的t 不具有一定的几何意义，但是在实际应用中有时能够简化某些运算.例如，动点M 做匀速直线运动，它在x 轴和y 轴方向的分速度分别为9和12，点M 从A 点(1，1)开始运动，求点M 的轨迹的参数方程.点M 的轨迹的参数方程可以直接写为⎩⎨⎧x ＝1＋9t ，y ＝1＋12t (t 为参数).【例1】 设直线的参数方程为⎩⎪⎨⎪⎧x ＝－4＋22t ，y ＝22t(t 为参数)，点P 在直线上，且与点M 0(－4，0)的距离为2，若该直线的参数方程改写成⎩⎨⎧x ＝－4＋t ，y ＝t (t 为参数)，则在这个方程中点P 对应的t 值为________. 解析 由|PM 0|＝2知t ＝±2，代入第一个参数方程，得点P 的坐标分别为(－3，1)或(－5，－1)，再把点P 的坐标代入第二个参数方程可得t ＝1或t ＝－1. 答案 ±1【反思感悟】 直线参数方程的标准形式中的参数具有相应的几何意义，本题正是使用了其几何意义，简化了运算，这也正是直线参数方程标准式的优越性所在.1.已知直线l 的方程为3x －4y ＋1＝0，点P (1，1)在直线l 上，写出直线l 的参数方程，并求点P 到点M (5，4)和点N (－2，6)的距离.解 由直线方程3x －4y ＋1＝0可知，直线的斜率为34，设直线的倾斜角为α，则tan α＝34，sin α＝35，cos α＝45.又点P (1，1)在直线l 上，所以直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋45t ，y ＝1＋35t(t 为参数). 因为3×5－4×4＋1＝0，所以点M 在直线l 上. 由1＋45t ＝5，得t ＝5，即点P 到点M 的距离为5.因为点N 不在直线l 上，故根据两点之间的距离公式，可得|PN |＝（1＋2）2＋（1－6）2＝34.【例2】 已知直线l 经过点P (1，1)，倾斜角α＝π6， (1)写出直线l 的参数方程；(2)设l 与圆x 2＋y 2＝4相交于两点A 、B ，求点P 到A 、B 两点的距离之积.解(1)直线的参数方程是⎩⎪⎨⎪⎧x ＝1＋32t ，y ＝1＋12t(t 是参数).(2)因为点A ，B 都在直线l 上，所以可设它们对应的参数为t 1和t 2，则点A ，B 的坐标分别为A ⎝ ⎛⎭⎪⎫1＋32t 1，1＋12t 1，B ⎝⎛⎭⎪⎫1＋32t 2，1＋12t 2.以直线l 的参数方程代入圆的方程x 2＋y 2＝4， 整理得到t 2＋(3＋1)t －2＝0.①因为t 1和t 2是方程①的解，从而t 1t 2＝－2. 所以|P A |·|PB |＝|t 1t 2|＝|－2|＝2.【反思感悟】 本题P 到A 、B 两点的距离就是参数方程中t 的两个值，可以充分利用参数的几何意义.2.已知直线l ：⎩⎪⎨⎪⎧x ＝－3＋32t ，y ＝2＋12t (t 为参数).(1)分别求t ＝0，2，－2时对应的点M (x ，y )； (2)求直线l 的倾斜角；(3)求直线l 上的点M (－33，0)对应的参数t ，并说明t 的几何意义.解(1)由直线l ：⎩⎪⎨⎪⎧x ＝－3＋32t ，y ＝2＋12t(t 为参数)知当t ＝0，2，－2时，分别对应直线l 上的点(－3，2)，(0，3)，(－23，1).(2)法一 化直线l ：⎩⎪⎨⎪⎧x ＝－3＋32t ，y ＝2＋12t(t 为参数)为普通方程为y －2＝33(x ＋3)，其中k ＝tan α＝33，0≤α<π. ∴直线l 的倾斜角α＝π6.法二由于直线l ：⎩⎪⎨⎪⎧x ＝－3＋t cos π6，y ＝2＋t sin π6(t 为参数)，这是过点M 0(－3，2)，且倾斜角α＝π6的直线，故π6为所求. (3)由上述可知直线l 的单位方向向量 e ＝⎝ ⎛⎭⎪⎫cos π6，sin π6＝⎝ ⎛⎭⎪⎫32，12. ∵M 0(－3，2)，M (－33，0)，∴M 0M →＝(－23，－2)＝－4⎝ ⎛⎭⎪⎫32，12＝－4e ， ∴点M 对应的参数t ＝－4，几何意义为|M 0M →|＝4， 且M 0M →与e 方向相反(即点M 在直线l 上点M 0的左下方).题型二 直线参数方程的应用利用直线的参数方程，可以求一些距离问题，特别是求直线上某一定点与曲线交点距离时使用参数的几何意义更为方便.【例3】 过点P ⎝ ⎛⎭⎪⎫102，0作倾斜角为α的直线与曲线x 2＋12y 2＝1交于点M ，N ，求|PM |·|PN |的最小值及相应的α的值. 解设直线为⎩⎨⎧x ＝102＋t cos α，y ＝t sin α(t 为参数)，代入曲线并整理得(1＋11sin 2α)t 2＋(10cos α)t ＋32＝0. 则|PM |·|PN |＝|t 1t 2|＝321＋11sin 2 α.所以当sin 2 α＝1时，即α＝π2，|PM |·|PN |的最小值为18，此时α＝π2.【反思感悟】 利用直线的参数方程中参数的几何意义，将最值问题转化为三角函数的值域，利用三角函数的有界性解决.3.已知曲线的参数方程⎩⎨⎧x ＝3cos θ，y ＝2sin θ(θ为参数)，求曲线上一点P 到直线⎩⎨⎧x ＝2－3t ，y ＝2＋2t(t 为参数)的最短距离. 解 P (3cos θ，2sin θ)直线：2x ＋3y －10＝0 d ＝|6cos θ＋6sin θ－10|13＝|62sin ⎝ ⎛⎭⎪⎫θ＋π4－10|1362sin ⎝ ⎛⎭⎪⎫θ＋π4－10∈[－62－10，62－10]∴|62sin ⎝ ⎛⎭⎪⎫θ＋π4－10|13∈⎣⎢⎡⎦⎥⎤10－6213，10＋6213 ∴d min ＝10－6213.【例4】 如图所示，过不在椭圆x 2a 2＋y 2b 2＝1上的任一点P 作两条直线l 1，l 2分别交椭圆于A ，B 和C ，D 四点，若l 1，l 2的倾斜角为α，β且满足α＋β＝π.求证：A ，B ，C ，D 四点共圆. 证明 设P (x 0，y 0)，直线l 1：⎩⎨⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α (t 为参数)，直线l 2：⎩⎨⎧x ＝x 0＋p cos β，y ＝y 0＋p sin β (p 为参数)，分别代入椭圆方程得(b 2cos 2 α＋a 2sin 2 α)t 2＋2(b 2x 0cos α＋a 2y 0sin α)t ＋b 2x 20＋a 2y 20－a 2b 2＝0； (b 2cos 2 β＋a 2sin 2 β)p 2＋2(b 2x 0cos β＋a 2y 0sin β)p ＋b 2x 20＋a 2y 20－a 2b 2＝0.∵α＋β＝π，∴cos 2 α＝cos 2 β，sin 2 α＝sin 2 β，∴t 1t 2＝p 1p 2，即|P A |·|PB |＝|PC |·|PD |.由平面几何知识知，A ，B ，C ，D 四点共圆. 【反思感悟】 本题利用平面几何知识，要证四点A ，B ，C ，D 共圆，只需证|P A |·|PB |＝|PC |·|PD |，又转化为距离问题，利用参数的几何意义计算即可.4.直线l 通过P 0(－4，0)，倾斜角α＝π6，l 与圆x 2＋y 2＝7相交于A ，B 两点. (1)求弦长|AB |；(2)过P 0作圆的切线，求切线长； (3)求|P 0A |和|P 0B |的长； (4)求交点A ，B 的坐标.解 ∵直线l 通过P 0(－4，0)，倾斜角α＝π6， 所以可设直线l 的参数方程为⎩⎪⎨⎪⎧x ＝－4＋32t ，y ＝t 2，代入圆方程，得⎝ ⎛⎭⎪⎫－4＋32t 2＋⎝ ⎛⎭⎪⎫12t 2＝7，整理得t 2－43t ＋9＝0.(1)设A ，B 对应的参数分别为t 1和t 2， 由根与系数的关系得t 1＋t 2＝43，t 1t 2＝9， ∴|AB |＝|t 2－t 1|＝（t 1＋t 2）2－4t 1t 2＝2 3. (2)设过P 0的切线为P 0T ，切点为T ， 则|P 0T |2＝|P 0A |·|P 0B |＝|t 1t 2|＝9， ∴切线长|P 0T |＝3.(3)解方程t 2－43t ＋9＝0，得t 1＝33，t 2＝3， ∴|P 0A |＝33，|P 0B |＝ 3.(4)将t 1＝33，t 2＝3代入直线参数方程⎩⎪⎨⎪⎧x ＝－4＋32t ，y ＝t 2，得A 点坐标为⎝ ⎛⎭⎪⎫12，332，B 点坐标为⎝ ⎛⎭⎪⎫－52，32. 题型三 圆的参数方程及其应用如果取半径绕原点O 逆时针旋转的转过的角度θ为参数，圆x 2＋y 2＝r 2对应的参数方程为⎩⎨⎧x ＝r cos θ，y ＝r sin θ.同理，圆(x －x 0)2＋(y －y 0)2＝r 2对应的参数方程为⎩⎨⎧x ＝x 0＋r cos θ，y ＝y 0＋r sin θ(θ为参数).圆的参数方程对于需要将圆上点的两个坐标分别表示，代入计算的问题比较方便. 【例5】 圆的直径AB 上有两点C 、D ，且|AB |＝10，|AC |＝|BD |＝4，P 为圆上一点，求|PC |＋|PD |的最大值.分析 本题应考虑数形结合的方法，因此需要先建立平面直角坐标系.将P 点坐标用圆的参数方程的形式表示出来，θ为参数，那么|PC |＋|PD |就可以用只含有θ的式子来表示，再利用三角函数等相关知识计算出最大值.解 以AB 所在直线为x 轴，以线段AB 的中点为原点建立平面直角坐标系.因为|AB |＝10，所以圆的参数方程为⎩⎨⎧x ＝5cos θ，y ＝5sin θ(θ为参数).因为|AC |＝|BD |＝4，所以C ，D 两点的坐标为C (－1，0)，D (1，0).因为点P 在圆上，所以可设点P 的坐标为(5cos θ，5sin θ). 所以|PC |＋|PD |＝（5cos θ＋1）2＋（5sin θ）2 ＋（5cos θ－1）2＋（5sin θ）2 ＝26＋10cos θ＋26－10cos θ ＝（26＋10cos θ＋26－10cos θ）2 ＝52＋2262－100cos 2 θ.当cos θ＝0时，(|PC |＋|PD |)max ＝52＋52＝226. ∴|PC |＋|PD |的最大值为226.【反思感悟】 解题时将所求式子和图形联系起来，利用圆的参数方程表示P 点坐标，结合三角函数的值域进行计算.5.已知实数x ，y 满足(x －1)2＋(y －1)2＝9，求x 2＋y 2的最大值和最小值.解 由已知，可把点(x ，y )视为圆(x －1)2＋(y －1)2＝9上的点，设⎩⎨⎧x ＝1＋3cos θ，y ＝1＋3sin θ(θ为参数).则x 2＋y 2＝(1＋3cos θ)2＋(1＋3sin θ)2 ＝11＋6(sin θ＋cos θ)＝11＋62sin ⎝ ⎛⎭⎪⎫θ＋π4∵－1≤sin ⎝ ⎛⎭⎪⎫θ＋π4≤1，∴11－62≤x 2＋y 2≤11＋6 2. ∴x 2＋y 2的最大值为11＋62， 最小值为11－6 2.1.求直线l 1：⎩⎨⎧x ＝1＋t ，y ＝－5＋3t (t 为参数)和直线l 2：x －y －23＝0的交点P 的坐标，及点P 与Q (1，－5)的距离.解 将⎩⎨⎧x ＝1＋t ，y ＝－5＋3t 代入x －y －23＝0，得t ＝23，∴P (1＋23，1)，而Q (1，－5)， 得|PQ |＝（23）2＋62＝4 3.2.已知直线l 的参数方程为⎩⎨⎧x ＝a －2t ，y ＝－4t (t 为参数)，圆C 的参数方程为⎩⎨⎧x ＝4cos θ，y ＝4sin θ(θ为参数).(1)求直线l 和圆C 的普通方程；(2)若直线l 与圆C 有公共点，求实数a 的取值范围.解 (1)直线l 的普通方程为2x －y －2a ＝0，圆C 的普通方程为x 2＋y 2＝16. (2)因为直线l 与圆C 有公共点，故圆C 的圆心到直线l 的距离d ＝|－2a |5≤4，解得－25≤a ≤2 5.3.已知椭圆的中心在原点，焦点在y 轴上且长轴长为4，短轴长为2，直线l 的参数方程为⎩⎨⎧x ＝t ，y ＝m ＋2t (t 为参数).当m 为何值时，直线l 被椭圆截得的弦长为6？解 椭圆方程为y 24＋x 2＝1，化直线参数方程⎩⎨⎧x ＝t ，y ＝m ＋2t 为⎩⎪⎨⎪⎧x ＝55t ′，y ＝m ＋255t ′ (t ′为参数). 代入椭圆方程得⎝ ⎛⎭⎪⎫m ＋255t ′2＋4⎝ ⎛⎭⎪⎫55t ′2＝4 ⇔8t ′2＋45mt ′＋5m 2－20＝0.当Δ＝80m 2－160m 2＋640＝640－80m 2>0， 即－22<m <22， 方程有两不等实根t ′1、t ′2，则弦长为|t ′1－t ′2|＝（t ′1＋t ′2）2－4t ′1t ′2＝640－80m 28，依题意知640－80m 28＝6，解得m ＝±455.[P 30思考交流]1.经过两点Q (1，1)，P (4，3)的直线的参数方程.如果应用共线向量的充要条件来求，方程及参数的含义分别是什么？答 在直线PQ 上任取一点M (x ，y )，PM→＝(x －1，y －1)，QM →＝(x －4，y －3)，∵P 、Q 、M 三点共线，∴PM→∥QM →，∴PM →＝tQM →，⎩⎪⎨⎪⎧x －1＝t （x －4），y －1＝t （y －3），化简为⎩⎪⎨⎪⎧x ＝1－4t 1－t，y ＝1－3t 1－t，此即为过P 、Q 两点的直线的参数方程.参数t 的含义是有向线段PM→、QM →的比值.2.比较直线的参数方程与普通方程体会各自的优势.答 直线的普通方程直观地反映了变量x、y 之间的关系，方程是唯一的. 直线的参数方程中反映了变量x 、y 分别随参数的变化而变化的规律.方程是不唯一的，随参数的选取而有所不同.[P 33思考交流]给定参数方程⎩⎨⎧x ＝a ＋r cos α，y ＝b ＋r sin α其中a 、b 是常数. 讨论下列问题：(1)如果r 是常数，α是参数，那么参数方程表示的曲线是什么？(2)如果α是常数，r 是参数，那么参数方程表示的曲线是什么？答 (1)⎩⎪⎨⎪⎧x ＝a ＋r cos α，y ＝b ＋r sin α⇒⎩⎪⎨⎪⎧x －a ＝r cos α，y －b ＝r sin α=====消掉参数α>(x －a )2＋(y －b )2＝r 2. 其中r 为常数，表示以(a ，b )为圆心，r 为半径的圆.(2)⎩⎪⎨⎪⎧x ＝a ＋r cos α，y ＝b ＋r sin α⇒⎩⎪⎨⎪⎧x －a ＝r cos α，y －b ＝r sin α=====消掉参数t >x －a y －b ＝tan α.整理得x －tan α·y ＋b ·tan α－a ＝0，其中a 、b 、tan α为常数.方程为过点(a ，b )，斜率为1tan α的直线.【规律方法总结】1.利用直线的参数方程⎩⎨⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(α为参数)中参数的几何意义，在解决直线与曲线交点问题时，可以方便地求出相应的距离.2.直线的参数方程有不同的形式，可以允许参数t 没有明显的几何意义，在直线与圆锥曲线的问题中，利用参数方程有时可以简化计算.一、选择题1.若直线的参数方程为⎩⎨⎧x ＝1＋2t ，y ＝2－3t(t 为参数)，则直线的斜率为( ) A.23 B.－23C.32D.－32 解析 k ＝y －2x －1＝－3t 2t ＝－32. 答案 D2.曲线⎩⎨⎧x ＝－1＋cos θ，y ＝2＋sin θ(θ为参数)的对称中心( ) A.在直线y ＝2x 上B.在直线y ＝－2x 上C.在直线y ＝x －1上D.在直线y ＝x ＋1上解析 消去参数θ，将参数方程化为普通方程.曲线可化为(x ＋1)2＋(y －2)2＝1，其对称中心为圆心(－1，2)，该点在直线y ＝－2x 上，故选B.答案 B3.直线⎩⎪⎨⎪⎧x ＝1＋12t ，y ＝－33＋32t(t 为参数)和圆x 2＋y 2＝16交于A ，B 两点，则AB 的中点坐标为( )A.(3，－3)B.(－3，3)C.(3，－3)D.(3，－3)解析 ⎝ ⎛⎭⎪⎫1＋12t 2＋⎝⎛⎭⎪⎫－33＋32t 2＝16， 得t 2－8t ＋12＝0，t 1＋t 2＝8，t 1＋t 22＝4， 中点为⎩⎪⎨⎪⎧x ＝1＋12×4，y ＝－33＋32×4，⇒⎩⎪⎨⎪⎧x ＝3，y ＝－ 3. 答案 D4.以平面直角坐标系的原点为极点，x 轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位.已知直线l 的参数方程是⎩⎨⎧x ＝t ＋1，y ＝t －3(t 为参数)，圆C 的极坐标方程是ρ＝4cos θ，则直线l 被圆C 截得的弦长为( ) A.14B.214C. 2D.2 2解析 直线l 的参数方程⎩⎪⎨⎪⎧x ＝t ＋1，y ＝t －3(t 为参数)化为直角坐标方程是y ＝x －4，圆C 的极坐标方程ρ＝4cos θ化为直角坐标方程是x 2＋y 2－4x ＝0.圆C 的圆心(2，0)到直线x －y －4＝0的距离为d ＝22＝ 2.又圆C 的半径r ＝2，因此直线l 被圆C 截得的弦长为2r 2－d 2＝2 2. 故选D.答案 D5.直线⎩⎨⎧x ＝t cos α，y ＝t sin α (t 为参数)与圆⎩⎨⎧x ＝4＋2cos θ，y ＝2sin θ(θ为参数)相切，则直线的倾斜角为( )A.π6或5π6B.π4或5π6C.π3或2π3D.－π6或－5π6 解析 直线方程为y ＝tan α·x ，圆为：(x －4)2＋y 2＝4，利用图形可知直线的倾斜角为π6或56π.答案 A二、填空题6.在平面直角坐标系中，曲线C ：⎩⎪⎨⎪⎧x ＝2＋22t ，y ＝1＋22t(t 为参数)的普通方程为________. 解析 ∵x ＝2＋22t ，∴22t ＝x －2，代入y ＝1＋22t ，得y ＝x －1，即x －y －1＝0.答案 x －y －1＝07.直线⎩⎪⎨⎪⎧x ＝2－12t ，y ＝－1＋12t(t 为参数)被圆x 2＋y 2＝4截得的弦长为________. 解析 直线为x ＋y －1＝0，圆心到直线的距离d ＝12＝22，弦长d ＝2 22－⎝ ⎛⎭⎪⎫222＝14. 答案 148.经过点P (1，0)，斜率为34的直线和抛物线y 2＝x 交于A 、B 两点，若线段AB 中点为M ，则M 的坐标为________.解析直线的参数方程为⎩⎪⎨⎪⎧x ＝1＋45t ，y ＝35t (t 是参数)，代入抛物线方程得9t 2－20t －25＝0.∴中点M 的相应参数为t ＝12×209＝109.∴点M 的坐标是⎝ ⎛⎭⎪⎫179，23. 答案 ⎝ ⎛⎭⎪⎫179，23 9.在直角坐标系xOy 中，以O 为极点，x 轴的正半轴为极轴建立极坐标系.已知直线l 的极坐标方程为ρ(sin θ－3cos θ)＝0，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝t －1t ，y ＝t ＋1t (t 为参数)，l 与C 相交于A ，B 两点，则|AB |＝________.解析 化极坐标方程为直角坐标方程，化参数方程为普通方程，联立直线l 和曲线C 的方程，求出交点A ，B 的坐标，利用两点间的距离公式求解.由ρ(sin θ－3cos θ)＝0，得ρsin θ＝3ρcos θ，则y ＝3x .由⎩⎪⎨⎪⎧x ＝t －1t ，y ＝t ＋1t ，得y 2－x 2＝4. 由⎩⎪⎨⎪⎧y ＝3x ，y 2－x 2＝4，可得⎩⎪⎨⎪⎧x ＝22，y ＝322或⎩⎪⎨⎪⎧x ＝－22，y ＝－322，不妨设A ⎝ ⎛⎭⎪⎫22，322，则B ⎝ ⎛⎭⎪⎫－22，－322， 故|AB |＝⎝ ⎛⎭⎪⎫－22－222＋⎝ ⎛⎭⎪⎫－322－3222＝2 5. 答案 2 5三、解答题10.直线过点A (1，3)，且与向量(2，－4)共线.(1)写出该直线的参数方程；(2)求点P (－2，－1)到此直线的距离.解 (1)设直线上任意一点坐标为(x ，y )，则(x ，y )＝(1，3)＋t (2，－4). ∴直线的参数方程为⎩⎨⎧x ＝1＋2t ，y ＝3－4t . (2)将参数方程化为普通方程为2x ＋y －5＝0，则|－4－1－5|5＝25， ∴点P (－2，－1)到此直线的距离是2 5.11.经过点A ⎝ ⎛⎭⎪⎫－3，－32，倾斜角为α的直线l 与圆x 2＋y 2＝25相交于B ，C 两点. (1)求弦BC 的长；(2)当A 恰为BC 的中点时，求直线BC 的方程；(3)当|BC |＝8时，求直线BC 的方程；(4)当α变化时，求动弦BC 的中点M 的轨迹方程.解 取AP ＝t 为参数(P 为l 上的动点)，则l 的参数方程为⎩⎪⎨⎪⎧x ＝－3＋t cos α，y ＝－32＋t sin α，代入x 2＋y 2＝25，整理，得t 2－3(2cos α＋sin α)t －554＝0.∵Δ＝9(2cos α＋sin α)2＋55>0恒成立.∴方程必有相异两实根t 1，t 2，且t 1＋t 2＝3(2cos α＋sin α)，t 1·t 2＝－554.(1)|BC |＝|t 1－t 2|＝（t 1＋t 2）2－4t 1t 2 ＝9（2cos α＋sin α）2＋55.(2)∵A 为BC 中点，∴t 1＋t 2＝0，即2cos α＋sin α＝0，∴tan α＝－2.故直线BC 的方程为y ＋32＝－2(x ＋3)，即4x ＋2y ＋15＝0.(3)∵|BC |＝9（2cos α＋sin α）2＋55＝8， ∴(2cos α＋sin α)2＝1，∴cos α＝0或tan α＝－34.∴直线BC 的方程是x ＝－3或3x ＋4y ＋15＝0.(4)∵BC 的中点M 对应的参数是t ＝t 1＋t 22＝32(2cos α＋sin α)，∴点M 的轨迹方程为⎩⎪⎨⎪⎧x ＝－3＋32cos α（2cos α＋sin α），y ＝－32＋32sin α（2cos α＋sin α）(0≤α<π)， ∴⎩⎪⎨⎪⎧x ＋32＝32⎝ ⎛⎭⎪⎫cos 2α＋12sin 2α，y ＋34＝32⎝ ⎛⎭⎪⎫sin 2α－12cos 2α.∴⎝ ⎛⎭⎪⎫x ＋322＋⎝ ⎛⎭⎪⎫y ＋342＝4516.即点M 的轨迹是以⎝ ⎛⎭⎪⎫－32，－34为圆心，以354为半径的圆.。

xx x第54讲 参数方程与 曲线系1．参数方程是联系多个变量之间关系的桥梁，在解题过程中引入参数或参数方程，使多个变量单一化，达到简化计算，解决问题的目的．几种常见的参数方程的形式如下：(1)直线的参数方程⎩⎨⎧x ＝x 0＋t cos θ，y ＝y 0＋t sin θ，（t 为参数）．其中θ是直线的倾斜角，参数t 表示有向线段AP →的数量（其中点A 、P 的坐标为A (x 0，y 0)，P (x ，y )），如图1所示．(2)圆的参数方程⎩⎨⎧x ＝x 0＋r cos θ，y ＝y 0＋r sin θ，（θ为参数）．其中r 是半径，圆心是(x 0，y 0)，参数θ表示圆心角，如图2所示．(3)椭圆参数方程⎩⎨⎧x ＝x 0＋a cos θ，y ＝y 0＋b sin θ，（θ为参数）．其中椭圆中心是(x 0，y 0)，长半轴长为a ，短半轴长为b (a ＞b )，参数θ表示离心(4)双曲线参数方程⎩⎨⎧x ＝x 0＋a sec θ，y ＝y 0＋b tan θ，（θ为参数）．其中双曲线中心是(x 0，y 0)，实半轴长为a ，虚半轴长为b ，θ是参数．(5)抛物线的参数方程为⎩⎨⎧x ＝2pt 2，y ＝2pt ，（t 为参数）．其中焦点为（p 2，0），准线为x ＝－p 2． 参数或参数方程在求轨迹方程，求极值，求变量取值范围，简化计算或证明方面具有突出的作用．2．常用的直线系方程：(1)过定点(x 0，y 0)的直线系为：λ1(y －y 0)＋λ2(x －x 0)＝0，其中λ1、λ2为参数．(2)与直线Ax ＋By ＋C ＝0平行的直线系为：Ax ＋By ＋λ＝0，其中λ≠C ，λ为参数．(3)与直线Ax ＋By ＋C ＝0垂直的直线系为：Bx －Ay ＋λ＝0，其中λ为参数．(4)当直线l 1与l 2的一般式分别为f 1(x ，y )＝0，f 2(x ，y )＝0时，曲线系λ1f1(x，y)＋λ2f2(x，y)＝0，其中λ1、λ2为参数①当l1与l2相交时表示通过l1与l2交点的所有直线；②当l1∥l2时，表示与l1平行的一组平行直线．(5)在两坐标轴上截距和为a的直线系为：xλ＋ya－λ＝1，其中λ为参数．(6)与原点距离等于r(r＞0)的直线系为：x cosθ＋y sinθ＝r，其中θ为参数．3．曲线系与圆系：(1)方程f1(x，y)＋ f2(x，y)＝0表示的曲线一定经过两条曲线f1(x，y)＝0与f2(x，y)＝0的交点．(反过来，经过它们交点的曲线不一定能用此方程表示)．当需要解决“求过两条曲线的交点作的一条曲线”时，常用此曲线系来解题，可以避免解方程组求交点而直接得出结果．(2)圆系：圆系是求圆的方程的一个重要的方法，同时也是证明四点共圆的简捷途径．对于不同圆心的两个圆C i＝x2＋y2＋D i x＋E i y＋F i＝0(i＝1，2)，则C1＋λC2＝0，(λ为参数)表示共轴圆系．当λ≠－1时，表示圆；当λ＝－1时，退化为一条直线(D1－D2)x＋(E1－E2)y＋(F1－F2)＝0，此直线叫两圆的根轴．对于已知圆C1及圆上一点（m，n），则C1＋λ[(x－m)2＋(y－n)2]＝0，(λ为参数)表示与C1相切于点（m，n）的圆系．4．二次曲线系：一般二次曲线的方程由6个参数确定：Ax2＋Bxy＋Cy2＋Dx＋Ey＋F＝0(A2＋B2＋C2≠0)．但只要5个独立参数即可确定唯一的二次曲线．①给定5个点，如果其中有三点共线，另两点不在此直线上，则经过此5点的二次曲线是唯一的，是二条直线(退化二次曲线)；②给定5个点，无三点共线，则经过此5点的二次曲线是唯一的．③若有两个二次曲线——C1：F1(x，y)＝0；C2：F2(x，y)＝0，且C1与C2交于不共线4点．则λF1(x，y)＋μF2(x，y)＝0表示所有经过此4个交点的二次曲线．5．用直线方程构成二次曲线系：①如果两条直线l i：l i(x，y)＝A i x＋B i y＋C i＝0(i＝1，2)与一条二次曲线：F(x，y)＝0有交点，那么，曲线系λF＋μl1·l2＝0经过这些交点，若它们有四个不共线的交点，则此曲线系包含所有的过此四点的二次曲线．②若有不共线4点P i(i＝1，2，3，4)，记直线P i P i＋1(P5＝P1)为l i(x，y)．则曲线系λl1·l3＋μl2·l4＝0包括了所有过此4点的二次曲线系．③若有不共线3点P i(i＝1，2，3)，记直线P i P i＋1(P4＝P1)为l i(x，y)．则曲线系λl1·l2＋μl2·l3＋ηl3·l1＝0包括了所有过此3点的二次曲线系．④与两条直线l i(x，y)＝A i x＋B i y＋C i＝0(i＝1，2)交于两点M1、M2的二次曲线系为λl1·l2＋μl32＝0．(其中l3为经过M1、M2的直线方程)．6．部分常用的二次曲线系：(1)共焦二次曲线系：x2m2－λ＋y2n2－λ＝1；(2)共顶点二次曲线系：x2a2＋y2λ＝1；(3)共离心率二次曲线系：x2a2＋y2b2＝λ(λ＞0)；(4)共渐近线的双曲线系：x2a2－y2b2＝λ．7．极线方程：从二次曲线外一点引二次曲线的切线，过两个切点的直线．利用曲线系解题实质上是取曲线方程中的特征量(如直线方程中的斜率k、截距b，圆的半径R，二次曲线中的a、b等)作为变量，得到曲线系，根据所给的已知量，采用待定系数法，达到解决问题的目的．常常体现的是参数变换的数学观点和整体处理的解题策略．通常的题型有求点的坐标，求曲线的方程，求图形的性质等等． A 类例题 例1．椭圆x 216＋y 24＝1有两点P 、Q ．O 是原点，若OP 、OQ 斜率之积为－14． 求证：|OP |2＋|OQ |2为定值．证明 设P (4cosα，2sinα)，Q (4cosβ，2sinβ)，因为k OP ·k OQ ＝－14，所以2sinα4cosα·2sinβ4cosβ＝－14，即cos(α－β)＝0，则α－β＝±π2＋2k π，k ∈Z ． 所以|OP |2＋|OQ |2＝16cos 2α＋4sin 2α＋16cos 2β＋4sin 2β＝16cos 2(β±π2)＋4sin 2(β±π2)＋16cos 2β＋4sin 2β ＝20cos 2β＋20sin 2β＝20为定值．得证．例2．求经过两直线2x －3y ＝1，3x ＋2y ＝2的交点，且平行于直线y ＋3x ＝0的直线方程．解 设所求的直线方程为(2x －3y －1)＋λ(3x ＋2y －2)＝0， 整理得 (2＋3λ)x ＋(－3＋2λ)y ＋(－1－2λ)＝0． (1)由于已知直线y ＋3x ＝0的斜率为－3，所以－2＋3λ－3＋2λ＝－3 解得λ＝113．将λ＝113代入(1)化简得39x ＋13y －25＝0． 此即为所求的直线方程．说明 本题还可以采用以下两种思路来求直线方程：思路一：设所求的直线方程为y ＋3x ＋λ＝0．解出直线2x －3y ＝1，3x ＋2y ＝2的交点，代入到y ＋3x ＋λ＝0，解出λ即可．思路二：过直线2x －3y ＝1，3x ＋2y ＝2的交点的直线系为(2x －3y －1)＋λ(3x ＋2y －2)＝0，即(2＋3λ)x ＋(－3＋2λ)y ＋(－1－2λ)＝0．与直线y ＋3x ＝0平行的直线系为y ＋3x ＋μ＝0(μ≠0)．比较系数2＋3λ3＝－3＋2λ1＝－1－2λμ，解出μ即可． 例3．抛物线y 2＝2px (p ＞0)的内接ΔAOB 的垂心为抛物线的焦点F ，O 为原点，求点A 、B 的坐标．解 由题设条件可知AB 与x 轴垂直．设A (2pt 2，2pt )，则B 的坐标为(2pt 2，－2pt )．由于焦点F 的坐标为F (p 2，0)， 则AF 的斜率为k 1＝2pt2pt 2－p 2＝4t4t 2－1； 而OB 的斜率为k 2＝－1t ． 因为AF 与OB 垂直，则k 1k 2＝－1，即4t 4t 2－1·(－1t )＝－1，解得t＝5 2．所以A的坐标为A(52p，5p)、B的坐标为B(52p，－5p)．情景再现1．已知有向线段PQ的起点P和终点Q的坐标分别为(－1，1)和(2，2)，若直线l：x＋my＋m＝0与PQ的延长线相交，则m的取值范围是．2．椭圆x2＋2y2＝2与直线x＋2y－1＝0交于B、C两点，求经过B、C及A(2，2)的圆的方程．3．若动点P(x，y)以等角速度ω在单位圆上逆时针运动，则点Q(－2xy，y2－x2)的运动方式是（）A．以角速度ω在单位圆上顺时针运动B．以角速度ω在单位圆上逆时针运动C．以角速度2ω在单位圆上顺时针运动D．以角速度2ω在单位圆上逆时针运动(1984年全国高中数学联赛)B类例题例4．斜率为3的动直线l和两抛物线y＝x2，y＝2x2－3x＋3交于四个不同的点，设这四个点顺次为A、B、C、D(如图)．求证：|AB|与|CD|之差为定值．证明 设AD 的中点为M (x 0，y 0)，因为直线l 的斜率为3，所以直线l 的参数方程为 ⎩⎨⎧x 0＝x 0＋12t ，y ＝y 0＋32t ．(t 为参数) ① 设MA ＝t 1，MD ＝t 2，MB ＝t 3，MC ＝t 4，则t 1＜t 2＜t 3＜t 4，因而|AB |－|CD |＝(t 3－t 1)－(t 2－t 4)＝(t 3＋t 4)－(t 1＋t 2) ②将①式代入y ＝x 2，整理得t 2＋4(x 0－32)t ＋4(x20－y 0)＝0， 由t 1＋t 2＝0，得x 0＝32． 将①式代入y ＝2x 2－3x ＋3，整理得t 2＋(4x 0－3－3)t ＋4(x 20－6x 0－2y 0＋6)＝0，所以t 3＋t 4＝－4x 0＋3＋3，因为x 0＝32，所以t 3＋t 4＝3－3， 代入②得：|AB |－|CD |＝3－3是定值．例5．设直线ax ＋by ＋c ＝0与抛物线y 2＝4px 相交于A 、B 两点，F 是抛物线的焦点，直线AF 、BF 交抛物线(异于A 、B 两点)于C、D两点(异于A、B两点)．求直线CD的方程．解设A(pt21，2pt1)、B(pt22，2pt2)、C(pt23，2pt3)、D(pt24，2pt3)．直线AC的方程为：y－2pt1＝2p(t1－t3)p(t21－t23))(x－pt21)，即2x－(t1＋t3)y＋2pt1t3＝0．因为AC经过焦点F(p，0)，所以t3＝－1t1；同理，t4＝－1t2．①因为点A、B在直线ax＋by＋c＝0上，则apt21＋2pbt1＋c＝0，apt22＋2pbt2＋c＝0，即t1、t2是方程apt2＋2pbt＋c＝0的两根．根据根与系数关系，得t1＋t2＝－2ba，t1t2＝cap．设CD的方程为ex＋fy＋g＝0 ②同理有t3＋t4＝－2fe，t1t2＝gep．所以－2fe＝－(1t1＋1t2)＝－t1＋t2t1t2＝2bpc，则f＝－bpec；gep＝1t1t2＝apc，则g＝ep2ac．把f＝－bpec，g＝ep2ac代入②，并整理得CD的方程为：x－bpy＋ap2＝0．例6．给定曲线族2(2sinθ－cosθ＋3)x2－(8sinθ＋cosθ＋1)y＝0，θ为参数，求该曲线在直线y＝2x上所截得的弦长的最大值．(1995年全国高中数学联赛)解显然，该曲线族恒过原点，而直线y＝2x也过原点，所以曲线族在y＝2x上所截得的弦长仅取决于曲线族与y＝2x的另一个交点的坐标．把y＝2x代入曲线族方程得(2sinθ－cosθ＋3)x2－(8sinθ＋cosθ＋1)x＝0，又2sinθ－cosθ＋3＝5sin(θ－arctan 12)＋3≠0，当x≠0时，就有x＝8sinθ＋cosθ＋12sinθ－cosθ＋3，(1)令sinθ＝2u1＋u2，cosθ＝1－u21＋u2，则x＝8u＋12u2＋2u＋1，得2xu2＋2(x－4)u＋(x－1)＝0．由u∈R知，当x≠0时Δ＝[2(x－4)]2－8x(x－1)＝4(－x2－6x ＋16)≥0，即x2＋6x－16≤0且x≠0，故－8≤x≤2且x≠0，则|x|max＝8由y ＝2x 得|y |max ＝16，所以所求弦长的最大值为82＋162＝85．说明 对于式(1)还可以这样处理：整理得(2x －8)sinθ－(x ＋1)cosθ＝1－3x ，于是只有当(2x －8)2＋(x ＋1)2≥(1－3x )2时方程才有解，即x 2＋6x －16≤0．以下同题中解法．情景再现4．在曲线y ＝51－x 29(－3≤x ≤3)上取一点，使它到直线x ＋y －10＝0的距离最远，并求出这个最远点．5．设a ，b 是两个已知正数，且a >b ，点P 、Q 在椭圆x 2a 2＋y 2b 2＝1上，若连结点A (－a ，0)与Q 的直线平行于直线OP ，且与y 轴交于点R ，则|AQ |·|AR ||OP |2＝ ；(O 为坐标原点)(上海市1992年高中数学竞赛)6．已知MN 是圆O 的一条弦，R 是MN 的中点，过R 作两弦AB 和CD ，过A 、B 、C 、D 四点的二次曲线MN 于P 、Q ．求证：R 是PQ 的中点． C 类例题例7．自点P 1向椭圆引两条切线，切点为Q 1、R 1，又自点P 2向这椭圆引两条切线，切点为Q 2、R 2．证明：P 1、Q 1、R 1、P 2、Q 2、R2六点在一条二次曲线上．解设椭圆方程为ax2＋by2＝1(a＞0，b＞0)，P1(x1，y1)，P2(x2，y2)．过切点Q1、R1的直线方程为ax1x＋by1y－1＝0，过切点Q2、R2的直线方程为ax2x＋by2y－1＝0，所以经过Q1、R1、Q2、R2的二次曲线方程可设为(ax1x＋by1y－1)(ax2x＋by2y－1)＋λ(ax2＋by2－1)＝0．令λ＝－(ax1x2＋by1y2－1)，得方程(ax1x＋by1y－1)(ax2x＋by2y－1)－(ax1x2＋by1y2－1)(ax2＋by2－1)＝0．显然点P1、P2的坐标满足此方程，而此方程是二次方程，即：P1、Q1、R1、P2、Q2、R2六点在一条二次曲线上．得证！例8．已知椭圆E：x2a2＋y2b2＝1(a＞b＞0)，动圆Γ：x2＋y2＝R2，其中b＜R＜a，若A是椭圆上的点，B是动圆Γ上的点，且使直线AB与椭圆和动圆Γ均相切，求A、B两点距离|AB|的最大值．(四川省2004年全国高中数学联赛预赛题)解设A(a cosθ，b sinθ)，则直线AB方程为(b2a cosθ)x＋(a2b sinθ)y＝a2b2即l：(b cosθ)x＋(a sinθ)y＝ab．l也是圆Γ的切线，故OB⊥l，故直线OB的方程为(a sinθ)x－(b cosθ)y＝0．于是点B坐标为B(ab2cosθb2cos2θ＋a2sin2θ，a2b sinθb2cos2θ＋a2sin2θ)．故|AB|2＝(a cosθ－ab2cosθb2cos2θ＋a2sin2θ)2＋(b sinθ－a2b sinθb2cos2θ＋a2sin2θ)2＝a2cos2θ(b2cos2θ+a2sin2θ－b2)2(b2cos2θ+a2sin2θ)2＋b2sin2θ(b2cos2θ+a2sin2θ－a2)2(b2cos2θ+a2sin2θ)2＝(a2－b2)2cos2θsin2θb2cos2θ+a2sin2θ＝(a－b)2·(a+b)2cos2θsin2θb2cos2θ+a2sin2θ．而b2cos2θ＋a2sin2θ≥(a+b)2cos2θsin2θ，等价于b2cos2θ－b2cos2θsin2θ+a2sin2θ－a2sin2θcos2θ≥2ab cos2θsin2θ，即b2cos4θ+a2sin4θ≥2ab cos2θsin2θ．最后一式显然成立．故|AB|2≤(a－b)2，即|AB|≤a－b．当且仅当tan2θ＝ba时等号成立，此时R＝|OB|＝ab．说明本题也可以这样考虑：设AB的斜率为k，由直线AB是椭圆E的切线，则AB方程为y＝kx±a2k2+b2．x 由AB 是圆Γ的切线，则AB 方程为y ＝kx ±R k 2+1．切点A 的横坐标x 1＝－ka 2m ；B 的横坐标x 2＝－kR 2m． 由a 2k 2+b 2＝R k 2+1，得k 2＝R 2－b 2a 2－R 2， 故|AB |2＝k 2m 2(a 2－R 2)2(1＋k 2)＝R 2－b 2a 2－R 2 (a 2－R 2)2R 2 ＝1R2(a 2－R 2)(R 2－b 2) ＝a 2＋b 2－R 2－a 2b 2R 2＝(a －b )2－(R －ab R )2≤(a －b )2． 从而可得上述结果．情景再现7．设P 、Q 为给定二次曲线ax 2＋bxy ＋cy 2＋dx ＋ey ＋f ＝0上任二点，过P 、Q 任作一圆，该圆与所给二次曲线交于另外两点M 、N ，求证：直线MN 有定向．(1978年上海市赛题) 8．如图，过点A (－2，m )作直线l 交椭圆x 22＋y 2＝1于B 、C ．点Q 在弦BC 上，且满足BQ QC ＝AB AC． (1)求m ＝0时，点Q 的轨迹方程；(2)若M 变动，则证明不论m 为何实数，点Q的轨迹恒过一个定点．习题541．设P是抛物线y2＝2x上的点，Q是圆(x－5)2＋y2＝1上的点，则|PQ|的最小值是；(上海市2001高中数学竞赛)2．与双曲线x29－y216=1有共同的渐近线，且经过点(－3，23)的双曲线方程是．(湖南省2001年高中数学竞赛)3．已知：双曲线的两条渐近线的方程为x＋y＝0和x－y＝0，两顶点间的距离为2，试求此双曲线方程．(1979年全国高中数学竞赛)4．当s和t取遍所有实数时，则(s＋5－3|cos t|)2＋(s－2|sin t|)2所能达到的最小值为．(1989年全国高中数学联赛) 5．求证：若轴垂直的两条抛物线如果有4个交点，则此四个交点共圆．(1979年河北省赛题)6．设AB、CD是椭圆x2a2＋y2b2＝1的两条弦，若它们的倾斜角互补，求证：A、B、C、D四点共圆．7．已知二次曲线C：Ax2＋Bxy＋Cy2＋Dx＋Ey＋F＝0与两条直线l1x＋m1y＋n1＝0，l2x＋m2y＋n2＝0有4个不同的交点．求证：Ax2＋Bxy＋Cy2＋Dx＋Ey＋F＋λ(l1x＋m1y＋n1)(l2x＋m2y＋n2)＝0（*）是过四个交点的曲线系．8．过不在圆锥圆锥上的一定点一定点P引已知圆锥曲线的任意相互垂直的两弦AB与CD．求证：1P A·PB＋1PC·PD是定值．本节“情景再现”解答：1．－3＜m＜－23．2．圆的方程为6x2＋6y2－9x－14y－2＝0．3．C．4．d max＝722，最远点为（－3，0）．5．2．6．以R为原点，MN为x轴，建立平面直角坐标系．设圆心O的坐标为(0，a)，圆半径为r，则原方程为x2＋(y－a)2＝r2①．设AB、CD的方程分别为y＝k1x和y＝k2x．将它们合成为(y－k1x)(y－k2x)＝0 ②．于是，过①与②的四个交点A、B、C、D的曲线系方程为(y－k1x)(y－k2x)＋λ[x2＋(y－a)2－r2]＝0③．令③中y＝0得，(λ＋k1k2)x2＋λ(a2－r2)＝0④．④的两个根是二次曲线与MN交点P、Q的横坐标．因为x P＋x Q＝0，x 即R 是PQ 的中点．7．以P 为原点，PQ 方向为x 轴正方向建立平面直角坐标系，且设Q (l ，0)，则所给二次曲线在此坐标系内的方程可以写为x 2＋b 'xy ＋c 'y 2－lx ＋e 'y ＝0．而过PQ 两点的圆方程为x 2＋y 2－lx ＋ky ＝0．于是曲线x 2＋b 'xy ＋c 'y 2－lx ＋e 'y ＋λ(x 2＋y 2－lx ＋ky )＝0过此二曲线交点．故必过另两个交点M 、N ．取λ＝－1代入得，b 'xy ＋(c '－1)y 2＋(e '－k )y ＝0，即y ＝0表示直线PQ ．方程b 'x ＋(c '－1)y ＋(e '－k )＝0表示直线MN ，由于b '、c '－有定向．8．设直线l 的参数方程为⎩⎨⎧x ＝－2＋t cosαy ＝m ＋t sinα，（t 为参数）．①代入椭圆方程，并整理得，(2sin 2α＋cos 2α)t 2＋4(m sinα－cosα)t ＋2(m 2＋1)＝0．所以，t 1＋t 2＝－4(m sinα－cosα)2sin 2α＋cos 2α，t 1t 2＝2(m 2＋1)2sin 2α＋cos 2α②． 设AB ＝t 1，AC ＝t 2，AQ ＝t ，则由BQ QC ＝AB AC ，得t －t 1t 1－t ＝t 1t 2，整理得，t (t 1＋t 2)＝2t 1t 2 ③，②代入③，得－t (m sinα－cosα)＝m 2＋1．t ＝m 2＋1cosα－m sinα④．将④代入①，得点Q 的轨迹的参数方程为⎩⎨⎧x ＝－2＋(m 2＋1)cosαcosα－m sinα，y ＝m ＋(m 2＋1)sinαcosα－m sinα，(α为参数)．消去α，得ym －(x ＋1)＝0． (1)当m ＝0时，所求轨迹是x ＝－1(过左焦点)被椭圆截下的弦；(2)当m 变动时，点Q 的轨迹恒过定点F 1(－1，0)．本节“习题4”解答：1．2． 2．x 29－y 216＝14． 3．双曲线方程为x 2－y 2＝±1． 4．2．5．设两条抛物线的方程分别为y 2＝2p (x －m )及x 2＝2q (y －n )．则曲线y 2－2p (x －m )＋λ[x 2－2q (y －n )]＝0必经过两条抛物线的交点，取λ＝1，即得一圆方程，由已知，此圆经过两条抛物线的四个交点．即此四个交点共圆．6．设AB 、CD 的倾斜角分别为θ与π－θ，直线AB 、CD 的交点坐标为P (x 0，y 0)，则AB 方程可写为⎩⎨⎧x ＝x 0＋t cosθ，y ＝y 0＋t sinθ．(θ为参数) 代入方程得：(b 2cos 2θ＋a 2sin 2θ)t 2＋2(b 2x 0cos θ＋a 2y 0sin θ)t ＋b 2x 02＋a 2y 02－a 2b 2＝0．由韦达定理知|P A |·|PB |＝|t 1t 2|＝|b 2x 20＋a 2y 20－a 2b 2|b 2cos 2θ＋a 2sin 2θ．以π－θ代替θ，即可得|PC |·|PD |＝|b 2x 20＋a 2y 20－a 2b 2|b 2cos 2θ＋a 2sin 2θ，即|P A |·|PB |＝|PC |·|PD |，故A 、B 、C 、D 共圆．7．设P i (x i ，y i )（i ＝1，2，3，4）为二次曲线C 与两条直线的四个交点，则Ax i 2＋Bx i y i ＋Cy i 2＋Dx i ＋Ey i ＋F ＝0（i ＝1，2，3，4），同时也有，l 1x i ＋m 1y i ＋n 1＝0，或l 2x i ＋m 2y i ＋n 2＝0．因此，这四个点的坐标满足（*），即（*）表示的曲线过曲线C 与直线的四个交点；在过已知四点P 1，P 2，P 3，P 4的任意一条二次曲线上取一点Q (x 0，y 0)，Q 与已知四点不同（它不在两已知直线上）．令λ0＝－Ax 02＋Bx 0y 0＋Cy 02＋Dx 0＋Ey 0＋F (l 1x 0＋m 1y 0＋n 1)(l 2x 0＋m 2y 0＋n 2)，方程（*）变形为Ax 2＋Bxy ＋Cy 2＋Dx ＋Ey ＋F ＋λ0(l 1x ＋m 1y ＋n 1)(l 2x ＋m 2y ＋n 2)＝0．这个方程表示过P 1，P 2，P 3，P 4，Q 五个点的曲线，故可用方程（*）表示已知二次曲线和两条直线交点的二次曲线系．8．以P 为原点建立直角坐标系，在此坐标系内圆锥曲线的方程为 Ax 2＋Bxy ＋Cy 2＋Dx ＋Ey ＋F ＝0． (1)P AB 的方程⎩⎨⎧x ＝x 0＋t cosθ，y ＝y 0＋t sinθ．(θ为参数)， 代入⑴得：t 2(A sin 2θ＋B sin θcos θ＋C cos 2θ)＋t (D sin θ＋E cos θ)＋F ＝0，由于P 不在圆锥曲线上，故F ≠0．则1P A ·PB ＝A sin 2θ＋B sin θcos θ＋C cos 2θF． PCD 的方程⎩⎨⎧x ＝－t sinθ，y ＝t cosθ．(θ为参数)， 代入(1)得：t 2(A cos 2θ－B sin θcos θ＋C sin 2θ)＋t (－D cos θ＋E sinθ)＋F＝0，同理，得，1PC·PD＝A cos2θ－B sinθcosθ＋C sin2θF．从而可得1P A·PB＋1PC·PD＝A＋CF为定值．第21 页共21 页。

直线和圆的方程知识要点一、直线方程.1. 直线的倾斜角：一条直线向上的方向与x 轴正方向所成的最小正角叫做这条直线的倾斜角，其中直线与x 轴平行或重合时，其倾斜角为0，故直线倾斜角的范围是)0(1800παα ≤≤.注：①当 90=α或12x x =时，直线l 垂直于x 轴，它的斜率不存在.②每一条直线都存在惟一的倾斜角，除与x 轴垂直的直线不存在斜率外，其余每一条直线都有惟一的斜率，并且当直线的斜率一定时，其倾斜角也对应确定.2. 直线方程的几种形式：点斜式、截距式、两点式、斜切式.特别地，当直线经过两点),0(),0,(b a ，即直线在x 轴，y 轴上的截距分别为)0,0(,≠≠b a b a 时，直线方程是：1=+b y a x . 注：若232--=x y 是一直线的方程，则这条直线的方程是232--=x y ，但若)0(232≥--=x x y 则不是这条线. 附：直线系：对于直线的斜截式方程b kx y +=，当b k ,均为确定的数值时，它表示一条确定的直线，如果b k ,变化时，对应的直线也会变化.①当b 为定植，k 变化时，它们表示过定点（0，b ）的直线束.②当k 为定值，b 变化时，它们表示一组平行直线.3. ⑴两条直线平行：1l ∥212k k l =⇔两条直线平行的条件是：①1l 和2l 是两条不重合的直线. ②在1l 和2l 的斜率都存在的前提下得到的. 因此，应特别注意，抽掉或忽视其中任一个“前提”都会导致结论的错误.（一般的结论是：对于两条直线21,l l ，它们在y 轴上的纵截距是21,b b ，则1l ∥212k k l =⇔，且21b b ≠或21,l l 的斜率均不存在，即2121A B B A =是平行的必要不充分条件，且21C C ≠） 推论：如果两条直线21,l l 的倾斜角为21,αα则1l ∥212αα=⇔l . ⑵两条直线垂直：两条直线垂直的条件：①设两条直线1l 和2l 的斜率分别为1k 和2k ，则有12121-=⇔⊥k k l l 这里的前提是21,l l 的斜率都存在. ②0121=⇔⊥k l l ，且2l 的斜率不存在或02=k ，且1l 的斜率不存在. （即01221=+B A B A 是垂直的充要条件）4. 直线的交角：⑴直线1l 到2l 的角（方向角）；直线1l 到2l 的角，是指直线1l 绕交点依逆时针方向旋转到与2l 重合时所转动的角θ，它的范围是),0(π，当 90≠θ时21121tan k k k k +-=θ. ⑵两条相交直线1l 与2l 的夹角：两条相交直线1l 与2l 的夹角，是指由1l 与2l 相交所成的四个角中最小的正角θ，又称为1l 和2l 所成的角，它的取值范围是 ⎝⎛⎥⎦⎤2,0π，当 90≠θ，则有21121tan k k k k +-=θ. 5. 过两直线⎩⎨⎧=++=++0:0:22221111C y B x A l C y B x A l 的交点的直线系方程λλ(0)(222111=+++++C y B x A C y B x A 为参数，0222=++C y B x A 不包括在内）6. 点到直线的距离：⑴点到直线的距离公式：设点),(00y x P ，直线P C By Ax l ,0:=++到l 的距离为d ，则有2200B A CBy Ax d +++=.注：1. 两点P 1(x 1,y 1)、P 2(x 2,y 2)的距离公式：21221221)()(||y y x x P P -+-=.特例：点P(x,y)到原点O 的距离：||OP = 2. 定比分点坐标分式。

第2章 2.2 直线和圆的参数方程2.2 直线和圆的参数方程 2.2.1 直线的参数方程 2.2.2 圆的参数方程1.理解直线的参数方程.(难点)2.掌握圆的参数方程.(重点)[基础·初探]1.直线的参数方程(1)经过点M 0(x 0，y 0)，倾斜角为α(α≠π2)的直线l 的参数方程为⎩⎨⎧x ＝x 0＋t cos αy ＝y 0＋t sin α(t 为参数)，其中参数t 的几何意义是：|t |是直线l 上任一点M (x ，y )到点M 0(x 0，y 0)的距离，即|t |＝|M 0M |.(2)设直线过点M 0(x 0，y 0)，且与平面向量a ＝(l ，m )平行(或称直线与a 共线，其中l ，m 都不为0)，直线的参数方程的一般形式为⎩⎨⎧x ＝x 0＋lt y ＝y 0＋mtt ∈R.2.圆的参数方程若圆心在点M 0(x 0，y 0)，半径为R ，则圆的参数方程为⎩⎨⎧x ＝x 0＋R cos θy ＝y 0＋R sin θ0≤θ≤2π.特别地，若圆心在原点，半径为R ，则圆的参数方程为⎩⎨⎧x ＝R cos θy ＝R sin θ.[思考·探究]1.若直线l 的倾斜角α＝0，则直线l 的参数方程是什么？ 【提示】 参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t ，y ＝y 0.2.如何理解直线参数方程中参数的几何意义？【提示】 过定点M 0(x 0，y 0)，倾斜角为α的直线l 的参数方程为∴⎩⎪⎨⎪⎧x ＝cos α ①y －1＝sin α ②(α为参数). ①2＋②2得x 2＋(y －1)2＝1，此即为所求普通方程. 【答案】 x 2＋(y －1)2＝14.若直线⎩⎨⎧x ＝1－2t y ＝2＋3t (t 为参数)与直线4x ＋ky ＝1垂直，则常数k ＝________.【解析】 将⎩⎪⎨⎪⎧x ＝1－2t y ＝2＋3t化为y ＝－32x ＋72，∴斜率k 1＝－32，显然k ＝0时，直线4x ＋ky ＝1与上述直线不垂直.∴k ≠0，从而直线4x ＋ky ＝1的斜率k 2＝－4k . 依题意k 1k 2＝－1，即－4k ×(－32)＝－1，∴k ＝－6.【答案】 －6[质疑·手记]预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流：疑问1： 解惑： 疑问2： 解惑： 类型一 直线的参数方程已知直线l ：⎩⎪⎨⎪⎧x ＝－3＋32t y ＝2＋12t (t 为参数).(1)求直线l 的倾斜角；(2)若点M (－33，0)在直线l 上，求t ，并说明t 的几何意义.【精彩点拨】 将直线l 的参数方程化为标准形式，求得倾斜角，利用参数的几何意义，求得t .【尝试解答】 (1)由于直线l ： ⎩⎪⎨⎪⎧x ＝－3＋t cos π6y ＝2＋t sin π6(t 为参数)表示过点M 0(－3，2)且倾斜角为π6的直线，故直线l 的倾斜角α＝π6.(2)由(1)知，直线l 的单位方向向量 e ＝(cos π6，sin π6)＝(32，12).∵M 0(－3，2)，M (－33，0)，∴M 0M →＝(－23，－2)＝－4(32，12)＝－4e ，∴点M 对应的参数t ＝－4，几何意义为|M 0M →|＝4，且M 0M →与e 方向相反(即点M 在直线l 上点M 0的左下方).1.一条直线可以由定点M 0(x 0，y 0)，倾斜角α(0≤α＜π)惟一确定，直线上的动点M (x ，y )的参数方程为⎩⎨⎧x ＝x 0＋t cos αy ＝y 0＋t sin α(t 为参数)，这是直线参数方程的标准形式.2.直线参数方程的形式不同，参数t 的几何意义也不同，过定点M 0(x 0，y 0)，斜率为ba 的直线的参数方程是⎩⎨⎧x ＝x 0＋at y ＝y 0＋bt (a 、b 为常数，t 为参数).[再练一题]1.设直线l 过点P (－3,3)，且倾斜角为5π6. 【导学号：62790011】(1)写出直线l 的参数方程；(2)设此直线与曲线C ：⎩⎨⎧x ＝2cos θy ＝4sin θ(θ为参数)交于A ，B 两点，求|PA |·|PB |.【解】 (1)直线l 的参数方程为 ⎩⎪⎨⎪⎧x ＝－3＋t cos 56π＝－3－32t y ＝3＋t sin 56π＝3＋t 2(t 为参数).(2)把曲线C 的参数方程中参数θ消去，得4x 2＋y 2－16＝0. 把直线l 的参数方程代入曲线C 的普通方程中，得 4⎝⎛⎭⎪⎫－3－32t 2＋(3＋12t )2－16＝0.即13t 2＋4(3＋123)t ＋116＝0. 由t 的几何意义，知 |PA |·|PB |＝|t 1·t 2|， 故|PA |·|PB |＝|t 1·t 2|＝11613. 类型二 圆的参数方程及应用设曲线C 的参数方程为⎩⎨⎧x ＝2＋3cos θy ＝－1＋3sin θ(θ为参数)，直线l 的方程为x －3y ＋2＝0，则曲线C 上到直线l 距离为71010的点的个数为( ) A.1 B.2 C.3D.4【精彩点拨】 求曲线C 的几何特征，化参数方程为普通方程(x －2)2＋(y ＋1)2＝9，根据圆心到直线l 的距离与半径大小作出判定.【尝试解答】 由⎩⎪⎨⎪⎧x ＝2＋3cos θ，y ＝－1＋3sin θ.得(x －2)2＋(y ＋1)2＝9.曲线C 表示以(2，－1)为圆心，以3为半径的圆， 则圆心C (2，－1)到直线l 的距离d ＝710＝71010<3，所以直线与圆相交.所以过圆心(2，－1)与l 平行的直线与圆的2个交点满足题意，又3－d <71010，故满足题意的点有2个.【答案】 B1.本题利用三角函数的平方关系，消去参数；数形结合，判定直线与圆的位置关系.2.参数方程表示怎样的曲线，一般是通过消参，得到普通方程来判断.特别要注意变量的取值范围.[再练一题]2.已知直线x ＝y ，与曲线⎩⎨⎧x ＝1＋2cos αy ＝2＋2sin α(α为参数)相交于两点A 和B ，求弦长|AB |.【解】 由⎩⎪⎨⎪⎧x ＝1＋2cos α，y ＝2＋2sin α.得⎩⎪⎨⎪⎧x －1＝2cos α，y －2＝2sin α.∴(x －1)2＋(y －2)2＝4，其圆心为(1,2)，半径r ＝2， 则圆心(1,2)到直线y ＝x 的距离d ＝|1－2|12＋(－1)2＝22. ∴|AB |＝2r 2－d 2＝2 22－(22)2＝14. 类型三 直线参数方程的简单应用已知直线的参数方程为⎩⎨⎧x ＝1＋2ty ＝2＋t(t 为参数)，则该直线被圆x 2＋y 2＝9截得的弦长是多少？【精彩点拨】 考虑参数方程标准形式中参数t 的几何意义，所以首先要把原参数方程转化为标准形式⎩⎪⎨⎪⎧x ＝1＋25 t ′，y ＝2＋15t ′，再把此式代入圆的方程，整理得到一个关于t 的一元二次方程，弦长即为方程两根之差的绝对值.【尝试解答】 将参数方程⎩⎪⎨⎪⎧x ＝1＋2t y ＝2＋t (t 为参数)转化为直线参数方程的标准形式为⎩⎪⎨⎪⎧x ＝1＋25 t ′y ＝2＋15t ′(t ′为参数).代入圆方程x 2＋y 2＝9， 得(1＋25 t ′)2＋(2＋15t ′)2＝9， 整理，得5t ′2＋8t ′－45＝0 由韦达定理，t ′1＋t ′2＝－85， t ′1·t ′2＝－4.根据参数t ′的几何意义. |t ′1－t ′2|＝(t ′1＋t ′2)2－4t ′1t ′2＝1255， 故直线被圆截得的弦长为1255. 在直线参数方程的标准形式下，直线上两点之间的距离可用|t 1－t 2|来求.本题易错的地方是：将题目所给参数方程直接代入圆的方程求解，忽视了参数t 的几何意义.[再练一题]3.若将条件改为“直线l 经过点A (1,2)，倾斜角为π3，圆x 2＋y 2＝9不变”，试求：(1)直线l 的参数方程；(2)直线l 和圆x 2＋y 2＝9的两个交点到点A 的距离之积.【解】(1)直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋t2y ＝2＋32t ，(t 为参数).(2)将⎩⎪⎨⎪⎧x ＝1＋t2y ＝2＋32t ，代入x 2＋y 2＝9，得t 2＋(1＋23)t －4＝0，∴t 1t 2＝－4.由参数t 的几何意义，得直线l 和圆x 2＋y 2＝9的两个交点到点A 的距离之积为|t 1t 2|＝4.[真题链接赏析](教材P 41习题2－2T 6)写出过点A (－1,2)，倾斜角为34π的直线的参数方程，并求该直线与圆x 2＋y 2＝8的交点.在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎨⎧x ＝a cos t ，y ＝1＋a sin t ，(t 为参数，a >0).在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线C 2：ρ＝4cos θ.(1)说明C 1是哪一种曲线，并将C 1的方程化为极坐标方程；(2)直线C 3的极坐标方程为θ＝α0，其中α0满足tan α0＝2，若曲线C 1与C 2的公共点都在C 3上，求a .【命题立意】 知识：曲线的参数方程与极坐标方程.能力：通过参数方程与极坐标方程的互化，考查转化与化归的数学思想方法.试题难度：中.【解】 (1)消去参数t 得到C 1的普通方程为x 2＋(y －1)2＝a 2，则C 1是以(0,1)为圆心，a 为半径的圆.将x ＝ρcos θ，y ＝ρsin θ代入C 1的普通方程中，得到C 1的极坐标方程为ρ2－2ρsin θ＋1－a 2＝0.(2)曲线C 1，C 2的公共点的极坐标满足方程组⎩⎪⎨⎪⎧ρ2－2ρsin θ＋1－a 2＝0，ρ＝4cos θ.若ρ≠0，由方程组得16cos 2θ－8sin θcos θ＋1－a 2＝0， 由已知tan θ＝2，可得16cos 2θ－8sin θcos θ＝0， 从而1－a 2＝0，解得a ＝－1(舍去)或a ＝1.当a ＝1时，极点也为C 1，C 2的公共点，且在C 3上. 所以a ＝1. 我还有这些不足：(1) (2) 我的课下提升方案：(1) (2)。

参数方程1.直线的参数方程(1)标准式 过点Po(x 0,y 0)，倾斜角为α的直线l(如图)的参数方程是(t 为参数) (2)一般式 ：过定点P 0(x 0,y 0)斜率k=tg α=的直线的参数方程是 (t 不参数) 2.圆的参数方程圆心在(a,b)，半径为r 的圆的参数方程是(φ是参数)a,b 是圆的圆心坐标，半径为r 的圆，标准方程为：3.椭圆椭圆(a ＞b ＞0)的参数方程是(φ为参数)得出圆的方程4.极坐标互化公式常用的公式：sin(α±β)＝sin αcos β±cos αsin β.⎩⎨⎧+=+=a t y y at x x sin cos 00ab⎩⎨⎧+=+=bt y y atx x 00⎩⎨⎧+=+=ϕϕsin cos r b y r a x ()()222r b y a x =-+-12222=+by a x ⎩⎨⎧==ϕϕsin cos b y a x 12222=+by a x ⎩⎨⎧=='sin cos θρθρy x ⎪⎩⎪⎨⎧≠=+=)0(222x x ytg y x θρcos(α±β)＝cos αcos β∓sin αsin β.1、已知直线的参数方程为，圆C 的参数方程为． (1)求直线和圆C 的普通方程； (2)若直线与圆C 有公共点，求实数的取值范围．2.. 在平面直角坐标系xOy 中，已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝1－22t ，y ＝2＋22t (t 为参数)，直线l 与抛物线y2＝4x 相交于A ，B 两点，求线段AB 的长．3在平面直角坐标系xOy 中, 直线的参数方程为(t 为参数),曲线C 的参数方程为 (为参数).试求直线和曲线C 的普通方程, 并求出它们的公共点的坐标.4.在直角坐标系中，以坐标原点为极点，x 轴的非负半轴为极轴建立极坐标系.已知点A 的极坐标为，直线的极坐标方程为，且点A 在直线上。