直线和圆的参数方程.ppt
- 格式:ppt
- 大小:734.54 KB
- 文档页数:25

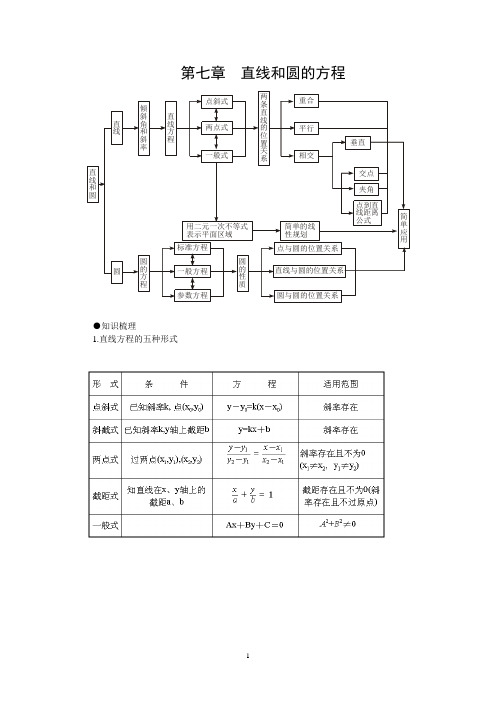
第七章直线和圆的方程●知识梳理1.直线方程的五种形式2.直线的倾斜角、斜率及直线的方向向量及位置关系:(1)直线的倾斜角在平面直角坐标系中,对于一条与x 轴相交的直线,如果把x 轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为α,那么α就叫做直线的倾斜角.直线和x 轴平行或重合时,直线的倾斜角为0°,直线倾斜角取值范围0°≤α<180°. (2)直线的斜率倾斜角α不是90°的直线,它的倾斜角的正切叫做这条直线的斜率,常用k 表示,即k =tan α(α≠90°).倾斜角是90°的直线没有斜率;倾斜角不是90°的直线都有斜率,其取值范围是(-∞,+∞).(4)求直线斜率的方法①定义法:已知直线的倾斜角为α,且α≠90°,则斜率k =tan α.②公式法:已知直线过两点P 1(x 1,y 1)、P 2(x 2,y 2),且x 1≠x 2,则斜率k =1212x x y y --.平面直角坐标系内,每一条直线都有倾斜角,但不是每一条直线都有斜率. 对于直线上任意两点P 1(x 1,y 1)、P 2(x 2,y 2),当x 1=x 2时,直线斜率k 不存在,倾斜角α=90°;当x 1≠x 2时,直线斜率存在,是一实数,并且k ≥0时,α=arctan k ,k <0时,α=π+arctan k .(5)到角与夹角:若直线l 1, l 2的斜率分别为k 1, k 2,将l 1绕它们的交点逆时针旋转到与l 2重合所转过的最小正角叫l 1到l 2的角;l 1与l 2所成的角中不超过900的正角叫两者的夹角。
若记到角为θ,夹角为α,则tan θ=21121k k k k +-,tan α=21121k k k k +-.(6)平行与垂直:若直线l 1与l 2的斜率分别为k 1, k 2。
且两者不重合,则l 1//l 2的充要条件是k 1=k 2;l 1⊥l 2的充要条件是k 1k 2=-1。


阶段一阶段二学业分层测评2.2 直线和圆的参数方程2.2.1 直线的参数方程2.2.2 圆的参数方程1.理解直线的参数方程. 难点2.掌握圆的参数方程. 重点[基础·初探]1.直线的参数方程(1)经过点M 0(x 0,y 0),倾斜角为±(±≠À2)的直线l 的参数方程为x =x 0+t cos ±y =y 0+t sin ±(t 为参数),其中参数t 的几何意义是:|t |是直线l 上任一点M (x ,y )到点M 0(x 0,y 0)的距离,即|t |=|M 0M |.(2)设直线过点M 0(x 0,y 0),且与平面向量a =(l ,m )平行(或称直线与a 共线,其中l ,m 都不为0),直线的参数方程的一般形式为x =x 0+lty =y 0+mtt ∈R .2.圆的参数方程若圆心在点M 0(x 0,y 0),半径为R ,则圆的参数方程为x =x 0+R cos ¸y =y 0+R sin ¸0≤¸≤2 À.特别地,若圆心在原点,半径为R ,则圆的参数方程为x =R cos ¸y =R sin ¸.[思考·探究]1.若直线l 的倾斜角±=0,则直线l 的参数方程是什么?【提示】参数方程为x =x 0+t ,y =y 0.2.如何理解直线参数方程中参数的几何意义? 【提示】 过定点M 0(x 0,y 0),倾斜角为±的直线l 的参数方程为x =x 0+t cos ±,y =y 0+t sin ±,(t 为参数),其中t 表示直线l 上以定点M 0为起点,任意一点M (x ,y )为终点的向量M 0M →的长度,即|t |=|M 0M →|.①当t >0时,M 0M →的方向向上; ②当t <0时,M 0M →的方向向下; ③当t =0时,点M 与点M 0重合.[自主·测评]1.直线x =1+t cos ±y =-2+t sin ±(±为参数,0≤±<À)必过点()A.(1,-2)B.(-1,2)C.(-2,1)D.(2,-1)【解析】 直线表示过点(1,-2)的直线. 【答案】 A2.已知直线l 的参数方程为x =-1-22ty =2+22t(t 为参数),则直线l 的斜率为()A.1B.-1C.22D.-22【解析】 消去参数t ,得方程x +y -1=0, ∴直线l 的斜率k =-1.【答案】 B3.参数方程x =cos ±y =1+sin ±(±为参数)化成普通方程为________.【解析】∵x =cos ±y =1+sin ±(±为参数),∴x =cos ±①y -1=sin ±②(±为参数).①2+②2得x 2+(y -1)2=1,此即为所求普通方程.【答案】 x 2+(y -1)2=14.若直线x =1-2ty =2+3t(t 为参数)与直线4x +ky =1垂直,则常数k =________.【解析】 将 x =1-2t y =2+3t 化为y =-32x +72,∴斜率k 1=-32,显然k =0时,直线4x +ky =1与上述直线不垂直.∴k ≠0,从而直线4x +ky =1的斜率k 2=-4k .依题意k 1k 2=-1,即-4k ×(-32)=-1,∴k =-6.【答案】 -6[质疑·手记]预习完成后,请将你的疑问记录,并与“小伙伴们”探讨交流:疑问1:_____________________________________________________ 解惑:_______________________________________________________ 疑问2:_____________________________________________________ 解惑:_______________________________________________________ 疑问3:______________________________________________________ 解惑:_______________________________________________________类型一 直线的参数方程已知直线l :x =-3+32ty =2+12t (t 为参数).(1)求直线l 的倾斜角;(2)若点M (-33,0)在直线l 上,求t ,并说明t 的几何意义.【精彩点拨】 将直线l 的参数方程化为标准形式,求得倾斜角,利用参数的几何意义,求得t .【尝试解答】 (1)由于直线l :x =-3+t cos À6y =2+t sin À6(t 为参数)表示过点M 0(-3,2)且倾斜角为À6的直线,故直线l 的倾斜角±=À6.(2)由(1)知,直线l 的单位方向向量e =(cos À6,sin À6)=(32,12).∵M 0(-3,2),M (-33,0),∴M 0M →=(-23,-2)=-4(32,12)=-4e ,∴点M 对应的参数t =-4,几何意义为|M 0M →|=4,且M 0M →与e 方向相反(即点M 在直线l 上点M 0的左下方).1.一条直线可以由定点M 0(x 0,y 0),倾斜角±(0≤±<À)惟一确定,直线上的动点M (x ,y )的参数方程为 x =x 0+t cos ±y =y 0+t sin ±(t 为参数),这是直线参数方程的标准形式.2.直线参数方程的形式不同,参数t 的几何意义也不同,过定点M 0(x 0,y 0),斜率为b a 的直线的参数方程是x =x 0+at y =y 0+bt (a 、b 为常数,t 为参数).[再练一题]1.设直线l 过点P (-3,3),且倾斜角为5 À6.【导学号:62790011】(1)写出直线l 的参数方程;(2)设此直线与曲线C : x =2cos ¸y =4sin ¸(¸为参数)交于A ,B 两点,求|PA |·|PB |.【解】 (1)直线l 的参数方程为x =-3+t cos 56À=-3-32t y =3+t sin 56À=3+t 2(t 为参数).(2)把曲线C 的参数方程中参数¸消去,得4x 2+y 2-16=0. 把直线l 的参数方程代入曲线C 的普通方程中,得 4-3-32t 2+(3+12t )2-16=0. 即13t 2+4(3+123)t +116=0.由t 的几何意义,知|PA |·|PB |=|t 1·t 2|,故|PA |·|PB |=|t 1·t 2|=11613.类型二 圆的参数方程及应用设曲线C 的参数方程为 x =2+3cos ¸y =-1+3sin ¸(¸为参数),直线l 的方程为x -3y +2=0,则曲线C 上到直线l 距离为71010的点的个数为() A.1B.2C.3D.4【精彩点拨】求曲线C的几何特征,化参数方程为普通方程(x-2)2+(y +1)2=9,根据圆心到直线l的距离与半径大小作出判定.【尝试解答】由 x =2+3cos ¸,y =-1+3sin ¸. 得(x -2)2+(y +1)2=9.曲线C 表示以(2,-1)为圆心,以3为半径的圆,则圆心C (2,-1)到直线l 的距离d =710=71010<3, 所以直线与圆相交.所以过圆心(2,-1)与l 平行的直线与圆的2个交点满足题意,又3-d <71010,故满足题意的点有2个.【答案】 B1.本题利用三角函数的平方关系,消去参数;数形结合,判定直线与圆的位置关系.2.参数方程表示怎样的曲线,一般是通过消参,得到普通方程来判断.特别要注意变量的取值范围.[再练一题]2.已知直线x =y ,与曲线 x =1+2cos ±y =2+2sin ±(±为参数)相交于两点A 和B ,求弦长|AB |.【解】 由 x =1+2cos ±,y =2+2sin ±.得 x -1=2cos ±,y -2=2sin ±. ∴(x -1)2+(y -2)2=4,其圆心为(1,2),半径r =2,则圆心(1,2)到直线y =x 的距离d =|1-2|12+ -12=22. ∴|AB |=2r 2-d 2=2 22- 22 2=14.类型三 直线参数方程的简单应用已知直线的参数方程为 x =1+2t y =2+t (t 为参数),则该直线被圆x 2+y 2=9截得的弦长是多少?【精彩点拨】 考虑参数方程标准形式中参数t 的几何意义,所以首先要把原参数方程转化为标准形式x =1+25 t ′,y =2+15 t ′,再把此式代入圆的方程,整理得到一个关于t 的一元二次方程,弦长即为方程两根之差的绝对值.【尝试解答】将参数方程 x =1+2t y =2+t (t 为参数)转化为直线参数方程的标准形式为x =1+25 t ′y =2+15t ′(t ′为参数). 代入圆方程x 2+y 2=9,得(1+25 t ′)2+(2+15t ′)2=9,整理,得5t′2+8t′-45=0由韦达定理,t′1+t′2=-85,t′1·t′2=-4.根据参数t′的几何意义.|t′1-t′2|= t′1+t′2 2-4t′1t′2=125 5,故直线被圆截得的弦长为125 5.在直线参数方程的标准形式下,直线上两点之间的距离可用|t1-t2|来求.本题易错的地方是:将题目所给参数方程直接代入圆的方程求解,忽视了参数t的几何意义.[再练一题]3.若将条件改为“直线l 经过点A (1,2),倾斜角为À3,圆x 2+y 2=9不变”,试求:(1)直线l 的参数方程;(2)直线l 和圆x 2+y 2=9的两个交点到点A 的距离之积.【解】 (1)直线l 的参数方程为x =1+t 2y =2+32t ,(t 为参数). (2)将 x =1+t 2y =2+32t ,代入x 2+y 2=9,得 t 2+(1+23)t -4=0,∴t 1t 2=-4.由参数t 的几何意义,得直线l 和圆x 2+y 2=9的两个交点到点A 的距离之积为|t 1t 2|=4.[真题链接赏析](教材P 41习题2-2T 6)写出过点A (-1,2),倾斜角为34À的直线的参数方程,并求该直线与圆x 2+y 2=8的交点.在直角坐标系xOy 中,曲线C 1的参数方程为 x =a cos t ,y =1+a sin t ,(t为参数,a >0).在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:Á=4cos ¸.(1)说明C 1是哪一种曲线,并将C 1的方程化为极坐标方程;(2)直线C 3的极坐标方程为¸=±0,其中±0满足tan ±0=2,若曲线C 1与C 2的公共点都在C 3上,求a .【命题立意】 知识:曲线的参数方程与极坐标方程.能力:通过参数方程与极坐标方程的互化,考查转化与化归的数学思想方法.试题难度:中.【解】(1)消去参数t得到C1的普通方程为x2+(y-1)2=a2,则C1是以(0,1)为圆心,a为半径的圆.将x=Ácos ¸,y=Ásin ¸代入C1的普通方程中,得到C1的极坐标方程为Á2-2Ásin ¸+1-a2=0.(2)曲线C 1,C 2的公共点的极坐标满足方程组Á2-2Ásin ¸+1-a 2=0,Á=4cos ¸.若Á≠0,由方程组得16cos 2¸-8sin ¸cos ¸+1-a 2=0,由已知tan ¸=2,可得16cos 2¸-8sin ¸cos ¸=0,从而1-a 2=0,解得a =-1(舍去)或a =1.当a =1时,极点也为C 1,C 2的公共点,且在C 3上.所以a =1.我还有这些不足:(1)________________________________________________________(2)________________________________________________________ 我的课下提升方案:(1)________________________________________________________(2)________________________________________________________学业分层测评(六)点击图标进入…。

