信阳师院结构力学静定梁和静定刚架习题

第3章　静定梁与静定刚架
3.1　复习笔记【知识框架】
【重点难点归纳】
一、单跨静定梁　★★★★
1．内力
表3-1-1　内力的基本概念
图3-1-1
图3-1-22．内力与外力间的微分关系及积分关系（1）由平衡条件导出的微分关系式
计算简图如图3-1-3所示，微分关系式为
（Ⅰ）
d d d d d d s
s N
F q x
x M F
x F p x
x ⎧=⎪⎪⎪=
⎨⎪⎪=-⎪⎩-（）（）
图3-1-3
（2）荷载与内力之间的积分关系
如图3-1-4
所示，结合式（Ⅰ）可得梁的内力积分公式，积分公式及其几何意义见表3-1-2。

图3-1-4
表3-1-2　内力的积分公式及几何意义
3．叠加法作弯矩图
表3-1-3　常用叠加法及其作图步骤
图3-1-5
图3-1-6
二、多跨静定梁　★★★★
多跨静定梁是由构造单元（如简支梁、悬臂梁）多次搭接而成的几何不变体系，其计算简图见图3-1-7，几何构造、计算原则、传力关系见表3-1-4。

0G
15 kN
F
80
67 kN 32
H
25
I
kN
8
结构力学电子教程
3 静定梁
2kN m
0C
D0
4kN
1kN 1kN
0A
9 kN 4
3、作剪力图
9/4
B 3 kN 0 0
4
E
25 kN 32
1kN/m
0G
15 kN
F
80
67 kN 32
H
25
I
kN
8
15/ 8
Q (kN) A
4、作弯矩图
A M (kN·m)
接画出M图。
P
B
CD
E
F
A
【解】
a
a
a
a
a
a
a
Pa
Pa
B
CD
E
A
Pa
结构力学电子教程
3 静定梁
结构力学（第二版）
包世华 主编
结构力学电子教程
3 静定梁
3.1 用叠加法作图示单跨静定梁的弯矩图。
(a)
A
P
Pl / 2
Pl/4
B
C
M
l/2
l/2
Pl / 4
【解】
Pl/4
A
B
C


P
A
B
C
Pl / 4 Pl / 4
3 静定梁
3.20 用分段叠加法作图示梁的弯矩图,并计算C点的弯矩值。
2kN/m
10kN
3kN
D
2m
A
C
2m 2m
B
E

第3章静定梁与静定刚架复习思考题1．用叠加法作弯矩图时，为什么是竖标的叠加，而不是图形的拼合？答：因为有时叠加弯矩图时的基线与杆轴不重合，如果用图形拼合，不能完全保证叠加后弯矩值是实际同一点的两个弯矩相加后的值。

2．为什么直杆上任一区段的弯矩图都可以用简支梁叠加法来作？其步骤如何？答：（1）因为根据内力分析可以求出直杆任一区段两端的内力，所以直杆任一区段两端均可以看成两端有外力（集中力或集中力偶）的简支梁。

（2）设有直杆任一区段简支梁AB，具体步骤如下①分解作用区段AB上的荷载；②分别作出分解荷载下的弯矩图；③求解出区段AB两端的弯矩M A和M B；④将两端弯矩M A和M B绘出并连以直线（虚线）；⑤以步骤④中的虚线为基线叠加各个分解荷载下的弯矩图（竖标叠加），得最终弯矩图。

3．试判断图3-1所示刚架中截面A、B、C的弯矩受拉边和剪力、轴力的正负号。

图3-1答：轴力以受压为负，受拉为正；剪力以使截面顺时针旋转为正。

（1）截面A：左边受拉，剪力为负，轴力为负；（2）截面B：右边受拉，剪力为正，轴力为正；（3）截面C：左边受拉，剪力为正，轴力为正。

4．怎样根据静定结构的几何构造情况（与地基按两刚片、三刚片规则组成，或具有基本部分与附属部分等）来确定计算反力的顺序和方法？答：（1）与地基按两刚片，例如简支梁，支座反力只有三个，对某一端点取矩直接解除约束反力。

（2）与地基按三刚片规则组成，例如三铰刚架，支座反力有四个，考虑结构整体的三个平衡方程外，还需再取刚架的左半部（或右半部，一般取外荷载较少部分）为隔离体建立一个平衡方程方可求出全部反力。

（3）具有基本部分与附属部分时，按先附属后基本的计算顺序，求解支座反力。

5．当不求或少求反力而迅速作出弯矩图时，有哪些规律可以利用？答：当不求或少求反力而迅速作出弯矩图时，如下规律可以利用（1）结构上若有悬臂部分及简支梁部分（含两端铰接直杆承受横向荷载）弯矩图可先行绘制出；（2）直杆的无荷区段弯矩图为直线和铰处弯矩为零；（3）刚结点的力矩平衡条件；（4）外力与杆轴重合时不产生弯矩；（5）外力与杆轴平行及外力偶产生的弯矩为常数；（6）对称性的合理利用；（7）区段叠加法作弯矩图。

２、截面法 若要求某一横截面上的内力，假想用一平面沿杆轴垂直方向将该 截面截开，使结构成两部分；在截开后暴露的截面上用力（内力）代 替原相互的约束。
对于截开后结构的两部分上，截面上的内力已成为外力，因此，
由任一部分的静力平衡条件，均可列出含有截面内力的静力平衡方程。 解该方程即将内力求出。
３、截面内力 截开一根梁式杆件的截面上有三个内力（分量），即：轴力ＦN 、 剪力ＦQ和弯矩Μ 。
dFN/dx=-qx
dFQ/dx=-qy dM/dx=Q
d2M/dx2=-qy
增量关系： DFN=-FPx
DFQ=-FPy
DM=m
１）微分关系及几何意义： dFN/dx=-qx dFQ/dx=-qy dM/dx=Q d2M/dx2=-qy （１）在无荷载区段，ＦQ图为水平直线；
当ＦQ≠０时，Μ图为斜直线;
右右为正。
ＦQ＝截面一侧所有外力在杆轴垂直方向上投影的代数和。左上为正， 右下为正。
Μ ＝截面一侧所有外力对截面形心力矩代数和。弯矩的竖标画在杆
件受拉一侧。
例3-1-1 求图（a）所示简支梁在图示荷载下截面的内力。
解：1）支座反力 ∑ΜA=0 FBy×4﹣10×4×2﹣100× (4/5)×2=0 Fby=60kN (↑) ∑ΜB=0 FAy=60kN (↑) ∑Fx= 0 FAx+100×(3/5)=0 FAx=－60kN (← ) 由 ∑Ｆy= 0 校核，满 足。
(下侧受拉)
区段叠加法求Ｅ、Ｄ截面弯矩； ΜE＝20×42/8＋120/2＝100kNm ΜＤ＝40×4/4＋120/2＝100kNm
(下侧受拉) (下侧受拉)
内力应考虑
说明：集中力或集中力偶作用点，注意对有突变的 分两侧截面分别计算。

M BC 2kNm
3、取AB为研究对象
MBA
或 取B节点为研究对象
2 kNm 2 kNm MBA
MBA=0
-4 kN
练习题
2
M
2
B
A 2m 1m
D
2m L P L L L L L
P
练习题
L
P L
P
L
P L
练习题
C
1kN/m
VC A VA 4m D
3、取AD为研究对象 B 4m
4m
VA
MDA VDA
3 kNm
3、取BCD为研究对象
2 kN
B
A 2m
C
D
1m
1m
MBC
1m
MBC= -1 kNm，上侧 1
MBA
1、取整体为研究对象
VC=4 kN
HA=2 kN 2、取AB为研究对象 MBA= - 2 kNm ,右侧受拉
B
2 A
C
D
练习题 2kN/m
C
8kN
20kNm 2m
3、BC为悬臂部分 MBC= 4 kNm，左侧
20 kN/m
4m
VB
MCB
MCD=90
MCF=135
VF
3.基本部分的计算，为悬臂杆。
VB=135
ME=135×3=405 kNm,左侧受拉
4. 作出弯矩图。
90 90
405
135
45
[习题3] 作弯矩图，剪力图，轴力图。
1.取整体为研究对象， ∑MA=0 ，VC×94×5-2×5×2.5=0 ， 解得VC= 5 kN ， ∑Y=0，VA=5 kN ∑X=0，HA=8 kN 8 kN 4 kN 2 kN/m HA VA VC

（二）绘内力图：
H A
=0
V
A =130KN
X 0 Y 0 M 0
C
NC 0 QC 130 KN M C 130 KN .M
第3章 例题: 试绘制图示外伸梁的内力图。
解：
10KN/m A HA=0 4m C 2m D B E 30KN.m 20KN
（1）计算支座反力
2m
2kN E
2m F
F
2m
G 2kN
2m
（b）
A
4kN/m B
C
G 2kN
G
B
11kN 4
4kN
4
（d）
8 7
（e） 9
4 M（kN.m） 2 2
Q（kN）
2
第3章 例题2： 图示三跨静定梁，全长承受均布荷载q，试确定铰E、F的位置，使中 间一跨支座的负弯矩与跨中正弯矩数据数值相等。
第3章
3.3 静定平面刚架的内力计算 一、刚架的组成 1、刚架的特征 由若干梁和柱用刚结点联结而成的结构。具有刚结点是 刚架的主要特征。 2、刚架的应用 刚架在工程上有广泛的应用。
（1）斜梁的倾角为常数，而曲梁各截面的的倾角是变量。 （2）计算曲梁的倾角时，可先写出曲梁的轴线方程y=f(x),而后对x求一 阶导数，进而确定倾角：
dy tan ; dx
tan1 (tan )
（3）角以由x轴的正方向逆时针转到切线方向时为正，反时针方向为负。
例题：试求图示曲梁C截面的内力值。已知曲梁轴线方程为：
y 4f 4 4 (l x) x 2 (12 1.5) 1.5 1.75m l2 12
4f 4 4 tan yx 1.5 2 (l 2 x) x1.5 2 (12 2 1.5) 1 l 12 2 450 sin con 0.707 2

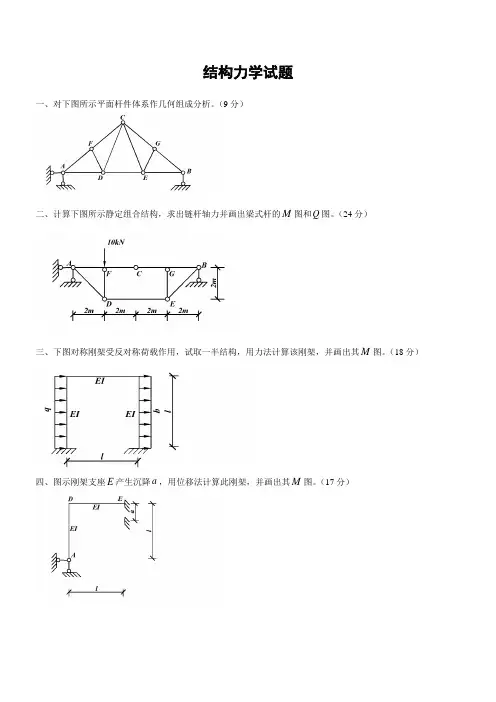
结构力学试题一、对下图所示平面杆件体系作几何组成分析。

（9分）二、计算下图所示静定组合结构，求出链杆轴力并画出梁式杆的M图和Q图。

（24分）三、下图对称刚架受反对称荷载作用，试取一半结构，用力法计算该刚架，并画出其M图。

（18分）四、图示刚架支座E产生沉降a，用位移法计算此刚架，并画出其M图。

（17分）五、用力矩分配法计算下图所示超静定刚架，并画出其M 图。

（17分）六、利用影响线求下图所示三跨静定梁D 支座的反力D R 。

（用其它方法不得分）。

（5分）结构力学试题参考答案及评分标准一、分析：基础以上部分与基础之间，用三根不交于一点也不完全平行的链杆相连，可只分析基础以上部分。

铰接ADF ∆和CDF ∆铰接BEG ∆和CEG ∆ 此体系几何不变，无多余约束。

二、解：先求出支座反力为 kN Y Y kN Y B A B 5.75.21010,5.28210=-=-==⨯=取出CGEB 部分为隔离体，其受力如右下图所示，由∑=0Cm024=⨯-⨯DE B S Y（1分）（2分） （2分） （1分） （3分）（2分）（2分）kN S DE 5=再以E 结点为对象，其受力如下图所示，由∑∑==0,0Y X45cos 045sin =+=-BE EG DE BE S S S S解出 kN S kN S EG BE 5,07.7-==（压）根据结点的对称性知kN S S kN S S EG DF BE AD 5,07.7-====（压）将梁式杆上引起弯矩和剪力的荷载标示如下图，再作出其弯矩图和剪力图。

三、解：此对称刚架受反对称荷载作用，取一半结构及其力法基本结构如下图：画出基本结构的P M 和1M 如下：（1分）（2分）（2分）（2分）（3分）（3分）（2分）（2分）（2分）（2分）EIl l l l l l l EI 2472223222211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯⨯⨯⨯=δEIql l ql l l l ql EI P122832222114221-=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯+⨯⨯⨯-⨯=∆ 721111qlX P=∆-=δ 由11M X M M P +=得此刚架的弯矩图如下图所示。

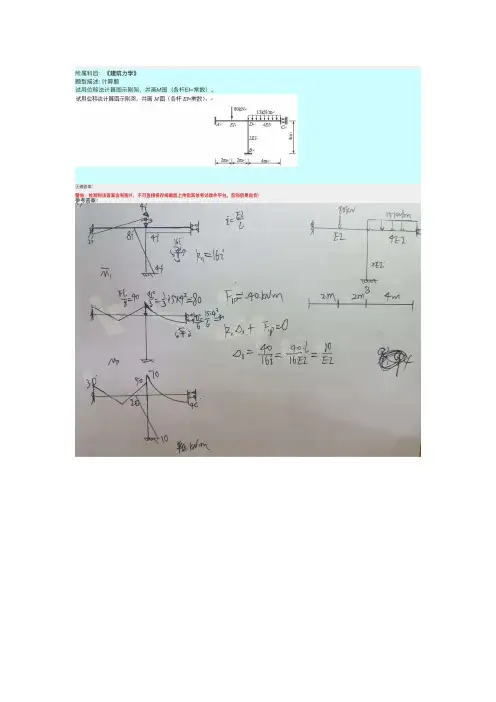
一、几何组成分析
二、作出图示静定梁的弯矩图。

三、弯矩图
四、绘图题
解：
五、弯矩图
六、试用位移法计算图示刚架，并作出M图（EI=常数）。

七、 弯矩图
八、 弯矩图
作出图示静定梁的弯矩图。

作出图示静定梁的弯矩图（不必写出作出过
程）
九、弯矩图
十、作出图示静定刚架的弯矩图。

十一、作出图示多跨静定梁的F Q K影响线。

十二、 弯矩图
十三、
试用力法解图示连续梁，并画弯矩图。

EI =常数。

（15分）（建议取图示基本结
构计算）。

十四、对称钢架作出M图
十五、钢架M图
十六、求图示体系的自振频率和主振型，并验算主振型的正交性。

十七、 作出图示静定刚架的弯矩图。

十八、 试用力法计算图示对称刚架，并作出M图。

=72/EI
常数。

二十、自振频率和主振型。

2、产生位移的原因主要有三种
3、变形体系的虚功原理:

a）荷载作用 b）温度改变和材料胀缩
c）支座沉降和制造误差
变形体虚功原理：各微段内力在应变上所作的内虚功总和Wv，
等于荷载在位移上以及支座反力在支座位移上所作的外虚功总
和W。
F + FRk ck = FN du + M d + FS ds
M
M
第四章
一、三铰拱的主要受力特点：
静定拱
在竖向荷载作用下，产生水平推力。 优点：水平推力的存在使拱截面弯矩减小，轴力增大； 截面应力分布较梁均匀。节省材料，自重轻能跨越大跨 度；截面一般只有压应力，宜采用耐压不耐拉的材料砖、 石、混凝土。使用空间大。 缺点：施工不便；增大了基础的材料用量。
二、反力计算公式：
FN FN P MM P EI ds + EA ds
8）该公式既用于静定结构和超静定结构。但必须是弹性体系 9）虚拟力状态：在拟求位移处沿着拟求位移的方向，虚设相应 的广义单位荷载。
A B 求A点的 水平位移 P=1 求A截面 的转角
m=1
m=1
m=1
P=1 求AB两点 的相对位移
P=1
教材57页(4-1)
注：1）该组公式仅用于：两底铰在同一水平线上且承受竖向荷载。 2）三铰拱的反力与跨度、矢高（即三铰的位臵）有关， 而与拱轴线的形状无关；水平推力与矢高成反比。
三、内力计算公式： 0 注：1、该组公式仅用于两底铰 FS = FS cos - FH sin 在同一水平线上,且承受 0 FN = - FS sin - FH cos 竖向荷载； 2、仍有 FS=dM/ds 即剪力等零处弯矩达极值； 3、 M、FS、FN图均不再为直线。 4、集中力作用处FS图将发生突变。 5、集中力偶作用处M图将发生突变。 四、三铰拱的合理轴线 在给定荷载作用下使拱内各截面弯矩 剪力等于零,只有轴力的拱轴线。合理拱轴线方程为：

B
qa / 2
Y 0: NCA qa / 2 0 NCA qa / 2 MC 0: MCA qa / 2a 0 MCA qa2 / 2
（右边受拉）
4m 2kN/m
4.11 计算题4-4图刚架结点C各杆截面内力。
10kN
A
C
B 解： NCA 0 QCA 3kN
3kN
7kN MCA 3 4 12kN m（下边受拉）
NAC 0 NBC 0 NDC 0
10kN B
C
3 A
7kN
8kN D 4m
Q (kN) 8
QCA 3kN QCB 7kN QCD 8 2 4 0
NCA 0 NCB 0 NCD 0
A N (kN)
C
B
7
D
B C
D
10kN
3kN C 7kN
4m 2kN/m
4.18 作图示刚架的内力图。
3m
A
B
2m 2m
6.31kN
C
9kN
2m 2m
9.69kN
MDC 6.31 4 331.5 8 2 4.26kN m （上边受拉）
NEF 0 QEF 8 9.69 1.69kN
1.69kN1.69kN
9kN 4.26kNm E
22.76kN m
9kN
27kN m
MEF 9.69 4 8 2 22.76kN m （下边受拉）
qa2
C2
C
D
qa2
q
a
qa
A
B
2 qa2 ()
8
3qa2 8
A M
a
qa / 2
qa / 2
C
D

第1章绪论（无习题）之阳早格格创做第2章仄里体系的机动领会习题解问习题利害推断题(1) 若仄里体系的本质自由度为整，则该体系一定为几许稳定体系.( )(2) 若仄里体系的估计自由度W=0，则该体系一定为无多余拘束的几许稳定体系.( )(3) 若仄里体系的估计自由度W＜0，则该体系为有多余拘束的几许稳定体系.( )(4) 由三个铰二二贯串的三刚刚片组成几许稳定体系且无多余拘束.( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后，结余部分为简收刚刚架，所以本质系为无多余拘束的几许稳定体系.( )习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后，成为习题2.1(6) (b)图，故本质系是几许可变体系.( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后，成为习题2.1(6) (c)图，故本质系是几许可变体系.( )习题 2.1(6)图习题挖空(1) 习题2.2(1)图所示体系为_________体系.习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系.习题 2-2(2)图(3) 习题2.2(3)图所示4个体系的多余拘束数目分别为_______、________、__________、__________.习题 2.2(3)图(4) 习题 2.2(4)图所示体系的多余拘束个数为___________.习题 2.2(4)图(5) 习题 2.2(5)图所示体系的多余拘束个数为___________.习题 2.2(5)图(6) 习题 2.2(6)图所示体系为_________体系，有_________个多余拘束.习题 2.2(6)图(7) 习题 2.2(7)图所示体系为_________体系，有_________个多余拘束.习题 2.2(7)图对付习题2.3图所示各体系举止几许组成领会.第3章静定梁与静定刚刚架习题解问习题利害推断题(1) 正在使用内力图特性画制某受直杆段的直矩图时，必须先供出该杆段二端的端直矩.（）(2) 区段叠加法仅适用于直矩图的画制，不适用于剪力图的画制.（）(3) 多跨静定梁正在附属部分受横背荷载效率时，必会引起基础部分的内力.（）(4) 习题3.1(4)图所示多跨静定梁中，CDE战EF部分均为附属部分.（）习题3.1(4)图习题挖空(1)习题3.2(1)图所示受荷的多跨静定梁，其定背通联C所传播的直矩M C的大小为______；截里B的直矩大小为______，____侧受推.习题3.2(1)图(2) 习题3.2(2)图所示风载效率下的悬臂刚刚架，其梁端直矩M AB=______kN·m，____侧受推；左柱B截里直矩M B=______kN·m，____侧受推.习题3.2(2)图习题做图所示单跨静定梁的M图战F图.Q(a) (b)(c) (d)(e) (f)习题做图所示单跨静定梁的内力图.(c) 习题做图所示斜梁的内力图.习题做图所示多跨梁的内力图.(a)(a)习题改正图所示刚刚架的直矩图中的过失部分.(a) (b) (c)(d) (e) (f)习题做图所示刚刚架的内力图.(a)(b)第4章静定拱习题解问习题4.1利害推断题(1) 三铰拱的火仄推力不但是与三个铰的位子有关，还与拱轴线的形状有关.（）(2) 所谓合理拱轴线，是指正在任性荷载效率下皆能使拱处于无直矩状态的轴线. （ ）(3) 改变荷载值的大小，三铰拱的合理拱轴线形状也将爆收改变. （ ）习题4.2挖空(1) 习题3.2(3)图所示三铰拱的火仄推力F H 等于.习题3.2(3)图习题4.3供图所示三铰拱收反力战指定截里K 的内力.已知轴线圆程24()f y x l x l =-.第5章 静定仄里桁架习题解问习题5.1 利害推断题(1) 利用结面法供解桁架结构时，可从任性结面启初. （ ） 习题5.2挖空(1)习题3.2(4)图所示桁架中有根整杆.习题3.2(4)图习题5.3 试用结面法供图所示桁架杆件的轴力.(a) (b)习题5.4 推断图所示桁架结构的整杆.(a) (b)(c)习题5.5 用截里法供解图所示桁架指定杆件的轴力.(a)(b)第6章 结构的位移估计习题解问习题6.1 利害推断题(1) 变形骸真功本理仅适用于弹性体系，不适用于非弹性体系.（ ）(2) 真功本理中的力状态战位移状态皆是真设的.（ ）(3) 功的互等定理仅适用于线弹性体系，不适用于非线弹性体系.（ ）(4) 反力互等定理仅适用于超静定结构，不适用于静定结构.（ ）(5) 对付于静定结构，有变形便一定有内力.（ ）(6) 对付于静定结构，有位移便一定有变形.（ ）(7) 习题4.1(7)图所示体系中各杆EA 相共，则二图中C 面的火仄位移相等.（ ）(8) M P 图，M 图如习题4.1(8)图所示，EI =常数.下列图乘截止是精确的：4)832(12l l ql EI ⨯⨯⨯ （ ）(9) M P 图、M (9)图所示，下列图乘截止是精确的：033202201111)(1y A EI y A y A EI ++ （ ）(10) (10)图所示结构的二个仄稳状态中，有一个为温度变更，此时功的互等定理不可坐.（ ）习题 4.1(7)图习题 4.1(8)图 习题4.1(9)图习题 4.1(10)图习题6.2挖空题(1) 习题4.2(1)图所示刚刚架，由于收座B 下重所引起D 面的火仄位移D H =______. (2) 真功本理有二种分歧的应用形式，即_______本理战_______本理.其中，用于供位移的是_______本理.(3) 用单位荷载法估计位移时，假制状态中所加的荷载应是与所供广义位移相映的________.(4) 图乘法的应用条件是：__________且M P 与M 图中起码有一个为直线图形.(5) 已知刚刚架正在荷载效率下的M P 图如习题4.2(5)图所示，直线为二次扔物线，横梁的抗直刚刚度为2EI ，横杆为EI ，则横梁中面K 的横背位移为________.(6) 习题4.2(6)图所示拱中推杆AB 比本安排少度短了，由此引起C 面的横背位移为________；引起收座A 的火仄反力为________.(7) 习题4.2(7)图所示结构，当C 面有F P =1(↓)效率时，D 面横背位移等于(↑)，当E 面有图示荷载效率时，C 面的横背位移为________.(8) 习题 4.2(8)图（a ）所示连绝梁收座B 的反力为)(1611R ↑=B F ，则该连绝梁正在收座B 下重B =1时（如图（b ）所示），D 面的横背位移D δ=________.习题 4.2(1)图 习题 4.2(5)图习题 4.2(6)图 习题 4.2(7)图习题 4.2(8)图习题6.3C V .EI 为常数.1)供C V习题4.3(1)图2)供C V习题4.3(2)图3)供C V习题4.3(3)图4)供A习题4.3（4）图习题6.4 分别用积分法战图乘法供习题4.4(a)图所示刚刚架C 面的火仄位移C H .已知EI =常数.习题6.5 习题4.5(a)图所示桁架各杆截里均为A =2×103m 2，E ×108kN/m 2，F P =30kN ，d =2m.试供C 面的横背位移V C .第7章 力法习题解问习题7.1利害推断题（1）习题5.1(1)图所示结构，当收座A 爆收转化时，D q l l B A C lA B lD C A BC22ql 2ql 281ql 2(b)图M P M 图(c)(a)xx1l各杆均爆收内力.（）习题5.1(1)图习题5.1(2)图（2）习题 5.1(2)图所示结构，当内中侧均降下t1℃时，二杆均只爆收轴力.（）（3）习题 5.1(3)图(a)战(b)所示二结构的内力相共.（）习题5.1(3)图（4）习题 5.1(3)图(a)战(b)所示二结构的变形相共.（）习题7.2 挖空题（1）习题5.2(1) 图(a)所示超静定梁的收座A爆收转角，若选图(b)所示力法基础结构，则力法圆程为_____________，代表的位移条件是______________，其中=_________；若选图(c)所示力法基础结构时，力法圆1c程为____________，代表的位移条件是______________，其中1c=_________.习题5.2(1)图（2）习题5.2(2)图(a)所示超静定结构，当基础体系为图(b)时，力法圆程为____________________，=________；当基础体系为图(c)时，力法圆程为1P____________________，1P=________.习题5.2(2)图（3）习题5.2(3)图(a)所示结构各杆刚刚度相共且为常数，AB杆中面直矩为________，____侧受推；图(b)所示结构M BC=________，____侧受推.习题5.2(3)图（4）连绝梁受荷载效率时，其直矩图如习题5.2(4)图所示，则D面的挠度为________，位移目标为____.习题5.2(4)图习题7.3试决定习题5.3图所示结构的超静定次数.图习题7.4用力法估计习题5.4图所示各超静定梁，并做出直矩图战剪力图.图习题7.5用力法估计习题5.5图所示各超静定刚刚架，并做出内力图.图习题7.6利用对付称性，估计习题5.12图所示各结构的内力，并画直矩图.图习题7.7画出习题5.17图所示各结构直矩图的大概形状.已知各杆EI=常数.图第8章位移法习题解问习题8.1决定用位移法估计图所示结构的基础已知量数目，并画出基础结构.（除证明者中，其余杆的EI为常数.）(a) (b) (c) (d)图习题8.2利害推断(1)位移法基础已知量的个数与结构的超静定次数无关.（）(2)位移法可用于供解静定结构的内力.（）(3)用位移法估计结构由于收座移动引起的内力时，采与与荷载效率时相共的基础结构.（）(4)位移法只可用于供解连绝梁战刚刚架，不克不迭用于供解桁架.（）习题8.3用位移法估计习题6.6图所示连绝梁，做直矩图战剪力图，EI=常数.(1)(2)习题8.4用位移法估计结构，做直矩图，EI=常数.(1)(2)第9章渐近法习题解问习题9.1利害推断题(1)力矩调配法不妨估计所有超静定刚刚架的内力.（）(2)习题7.1(2)图所示连绝梁的蜿蜒刚刚度为EI，杆少为l，杆端直矩M BC<M.（）习题7.1(2)图习题7.1(3)图(3)习题7.1(3)图所示连绝梁的线刚刚度为i，欲使A端爆收逆时针单位转角，需施加的力矩M A>3i.（）习题9.2挖空题(1)习题7.2(1)图所示刚刚架EI=常数，各杆少为l，杆端直矩M AB =________.(2)习题7.2(2)图所示刚刚架EI=常数，各杆少为l，杆端直矩M AB =________.(3)习题7.2(3)图所示刚刚架各杆的线刚刚度为i，欲使结面B爆收逆时针的单位转角，应正在结面B施加的力矩M B =______.习题7.2(1)图习题7.2(2)图习题7.2(3)图(4)用力矩调配法估计习题7.2(4)图所示结构（EI=常数）时，传播系数C BA =________，C BC =________.习题7.2(4)图习题9.3用力矩调配法估计习题7.3图所示连绝梁，做直矩图战剪力图，并供收座B的反力.（1）（2）习题9.4用力矩调配法估计习题7.4图所示连绝梁，做直矩图.（1）（2）习题9.5用力矩调配法估计习题7.5图所示刚刚架，做直矩图.（1）（2）第11章效率线及其应用习题解问习题11.1利害推断题(1)习题8.1(1)图示结构BC杆轴力的效率线应画正在BC杆上.（）习题8.1(1)图习题8.1(2)图(2) 习题8.1(2)图示梁的M C效率线、F Q C效率线的形状如图（a）、（b）所示.(3) 习题8.1(3)图示结构，利用M C效率线供牢固荷载F P1、F P2、F P3效率下M C的值，可用它们的合力F R去代替，即M C= F P1y1+ F P2y2+ F P3y3=F R y.( )习题8.1(3)图(4) 习题8.1(4)图中的（a）所示主梁F Q C左的效率线如图（b）所示.( )习题8.1(4)图(5)习题8.1(5)图示梁F R A的效率线与F Q A左的效率线相共.( )习题8.1(5)图(6) 简收梁的直矩包络图为活载效率下各截里最大直矩的连线.( )习题11.2挖空题(1) 用静力法做效率线时，其效率线圆程是.用机动法做静定结构的效率线，其形状为机构的.(2) 直矩效率线横目标量目是.(3)习题8.2(3)图所示结构，F P=1沿AB移动，M D的效率线正在B面的横标为，F Q D的效率线正在B面的横标为.习题8.2(3)图(4) 习题8.2(4)图所示结构，F P=1沿ABC移动，则M D 效率线正在B面的横标为.习题8.2(4)图(5)习题8.2(5)图所示结构，F P=1沿AC移动，截里B的轴力F N B的效率线正在C面的横标为.习题8.2(5)图习题11.3单项采用题(1)习题8.3(1)图所示结构中收座A左侧截里剪力效率线的形状为( ).习题8.3(1)图(2) 习题8.3(2)图所示梁止家列荷载效率下，反力F R A的最大值为( ).(a) 55kN (b) 50kN (c) 75kN (d) 90kN习题8.3(2)图(3)习题8.3(3)图所示结构F Q C效率线(F P=1正在BE上移动)BC、CD段横标为( ).(a) BC,CD均不为整； (b) BC,CD均为整；(c) BC为整,CD不为整；(d) BC不为整,CD为整.习题8.3(3)图(4)习题8.3(4)图所示结构中，收座B左侧截里剪力效率线形状为( ).习题8.3(4)图(5)习题8.3(5)图所示梁止家列荷载效率下，截里K的最大直矩为( ).(a) 15kN·m(b) 35 kN·m(c) 30 kN·m(d) kN·m习题8.3(5)图习题11.4做习题8.4(a)图所示悬臂梁F R A、M C、F Q C的效率线.习题11.5做习题8.5(a)图所示结构中F N BC、M D的效率线，F P =1正在AE上移动.习题11.6做习题8.6(a)图所示伸臂梁的M A、M C、F Q A 左、F Q A左的效率线.习题11.7做习题8.7(a)图所示结构中截里C的M C、F Q C的效率线.习题11.8(a)图所示静定多跨梁的F R B、M E、F Q B左、F Q B左、F Q C的效率线.习题11.9(a)图所示牢固荷载效率下截里K的内力M K战F Q K左.习题11.10(a)图所示连绝梁M K、M B、F Q B左、F Q B左效率线的形状.若梁上有随意安插的均布活荷载，请画出使截里K爆收最大直矩的荷载安插.第2章仄里体系的机动领会习题解问习题利害推断题(1) 若仄里体系的本质自由度为整，则该体系一定为几许稳定体系.( )(2) 若仄里体系的估计自由度W=0，则该体系一定为无多余拘束的几许稳定体系.( )(3) 若仄里体系的估计自由度W＜0，则该体系为有多余拘束的几许稳定体系.( )(4) 由三个铰二二贯串的三刚刚片组成几许稳定体系且无多余拘束.( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后，结余部分为简收刚刚架，所以本质系为无多余拘束的几许稳定体系.( )习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后，成为习题2.1(6) (b)图，故本质系是几许可变体系.( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后，成为习题2.1(6) (c)图，故本质系是几许可变体系.( )习题 2.1(6)图【解】（1）精确.（2）过失.0W 是使体系成为几许稳定的需要条件而非充分条件.（3）过失.（4）过失.惟有当三个铰不共线时，该题的论断才是精确的.（5）过失.CEF不是二元体.（6）过失.ABC不是二元体.（7）过失.EDF不是二元体.习题挖空(1) 习题2.2(1)图所示体系为_________体系.习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系.习题 2-2(2)图(3) 习题2.2(3)图所示4个体系的多余拘束数目分别为_______、________、__________、__________.习题 2.2(3)图(4) 习题 2.2(4)图所示体系的多余拘束个数为___________.习题 2.2(4)图(5) 习题 2.2(5)图所示体系的多余拘束个数为___________.习题 2.2(5)图(6) 习题 2.2(6)图所示体系为_________体系，有_________个多余拘束.习题 2.2(6)图(7) 习题 2.2(7)图所示体系为_________体系，有_________个多余拘束.习题 2.2(7)图【解】（1）几许稳定且无多余拘束.安排二边L形杆及大天分别动做三个刚刚片.（2）几许常变.中间三铰刚刚架与大天形成一个刚刚片，其与左边倒L形刚刚片之间惟有二根链杆相联，缺少一个拘束.（3）0、1、2、3.末尾一个启关的圆环（大概框）里里有3个多余拘束.（4）4.表层可瞅做二元体去掉，下层多余二个铰.（5）3.下层（包罗大天）几许稳定，为一个刚刚片；与表层刚刚片之间用三个铰相联，多余3个拘束.（6）里里几许稳定、0.将左上角火仄杆、左上角铰交三角形战下部铰交三角形分别动做刚刚片，根据三刚刚片准则领会.（7）里里几许稳定、3.中围启关的正圆形框为有3个多余拘束的刚刚片；里里铰交四边形可选一对付仄止的对付边瞅做二个刚刚片；根据三刚刚片准则即可领会.对付习题2.3图所示各体系举止几许组成领会.【解】（1）如习题解2.3(a)图所示，刚刚片AB与刚刚片I 由铰A战收杆①相联组成几许稳定的部分；再与刚刚片BC 由铰B战收杆②相联，故本质系几许稳定且无多余拘束.习题解2.3(a)图（2）刚刚片Ⅰ、Ⅱ、Ⅲ由不共线三铰A、B、（Ⅰ，Ⅲ）二二相联，组成几许稳定的部分，如习题解2.3(b)图所示.正在此部分上增加二元体C-D-E，故本质系几许稳定且无多余拘束.习题解2.3(b)图（3）如习题解2.3(c)图所示，将左、左二端的合形刚刚片瞅成二根链杆，则刚刚片Ⅰ、Ⅱ、Ⅲ由不共线三铰（Ⅰ，Ⅱ）、（Ⅱ，Ⅲ）、（Ⅰ，Ⅲ）二二相联，故体系几许稳定且无多余拘束.习题解2.3(c)图（4）如习题解2.3(d)图所示，刚刚片Ⅰ、Ⅱ、Ⅲ由不共线的三铰二二相联，产死大刚刚片；该大刚刚片与天基之间由4根收杆贯串，有一个多余拘束.故本质系为有一个多余拘束的几许稳定体系.习题解2.3(d)图（5）如习题解2.3(e)图所示，刚刚片Ⅰ、Ⅱ、Ⅲ组成几许稳定且无多余拘束的体系，为一个大刚刚片；该大刚刚片与天基之间由仄止的三根杆①、②、③相联，故本质系几许瞬变.习题解2.3(e)图（6）如习题解2.3(f)图所示，由三刚刚片准则可知，刚刚片Ⅰ、Ⅱ及天基组成几许稳定且无多余拘束的体系，设为夸大的天基.刚刚片ABC与夸大的天基由杆①战铰C相联；刚刚片CD与夸大的天基由杆②战铰C相联.故本质系几许稳定且无多余拘束.习题解2.3(f)图第3章静定梁与静定刚刚架习题解问习题利害推断题(1) 正在使用内力图特性画制某受直杆段的直矩图时，必须先供出该杆段二端的端直矩.（）(2) 区段叠加法仅适用于直矩图的画制，不适用于剪力图的画制.（）(3) 多跨静定梁正在附属部分受横背荷载效率时，必会引起基础部分的内力.（）(4) 习题3.1(4)图所示多跨静定梁中，CDE战EF部分均为附属部分.（）习题3.1(4)图【解】（1）精确；（2）过失；（3）精确；（4）精确；EF为第二条理附属部分，CDE为第一条理附属部分；习题挖空(1)习题3.2(1)图所示受荷的多跨静定梁，其定背通联C所传播的直矩M C的大小为______；截里B的直矩大小为______，____侧受推.习题3.2(1)图(2) 习题3.2(2)图所示风载效率下的悬臂刚刚架，其梁端直矩M AB=______kN·m，____侧受推；左柱B截里直矩M B=______kN·m，____侧受推.习题3.2(2)图【解】（1）M C = 0；M C = F P l，上侧受推.CDE部分正在该荷载效率下自仄稳；（2）M AB=288kN·m，左侧受推；M B=32kN·m，左侧受推；习题做图所示单跨静定梁的M图战F图.Q(a) (b)(c) (d)(e) (f)【解】M图（单位：kN·m）F Q图（单位：kN）(a)M图F Q图(b)M图F Q 图(c)M图F Q图(d)M图F Q图(e)M图（单位：kN·m）F Q图（单位：kN）(f)习题做图所示单跨静定梁的内力图.(c) 【解】M图（单位：kN·m）F Q图（单位：kN）(c)习题做图所示斜梁的内力图.【解】M图（单位：kN·m）F Q图（单位：kN）F N图（单位：kN）习题做图所示多跨梁的内力图.(a)【解】M图（单位：kN·m）F Q图（单位：kN）(a)习题3.7 改正图所示刚刚架的直矩图中的过失部分.(a) (b) (c)(d) (e) (f)【解】(a) (b) (c)(d) (e) (f)习题做图所示刚刚架的内力图.(a)(b)【解】M图（单位：kN·m）F Q图（单位：kN）F N图（单位：kN）(a)M图（单位：kN·m）F Q图（单位：kN）F N图（单位：kN）(b)第4章静定拱习题解问习题4.1利害推断题(1) 三铰拱的火仄推力不但是与三个铰的位子有关，还与拱轴线的形状有关.（）(2) 所谓合理拱轴线，是指正在任性荷载效率下皆能使拱处于无直矩状态的轴线. （）(3) 改变荷载值的大小，三铰拱的合理拱轴线形状也将爆收改变. （ ） 【解】（1）过失.从公式0H /C F M f =可知，三铰拱的火仄推力与拱轴线的形状无关；（2）过失.荷载爆收改变时，合理拱轴线将爆收变更； （3）过失.合理拱轴线与荷载大小无关； 习题4.2挖空(1) 习题3.2(3)图所示三铰拱的火仄推力F H 等于.习题3.2(3)图【解】（1）F P /2；习题4.3供图所示三铰拱收反力战指定截里K 的内力.已知轴线圆程24()fy x l x l=-.【解】H H 16kN A B F F ==;VA 8kN()F =↑;V 24kN()B F =↑ 15kN m K M =-⋅;Q 1.9kN K F =;N 17.8kN K F =-第5章 静定仄里桁架习题解问习题5.1 利害推断题(1) 利用结面法供解桁架结构时，可从任性结面启初. （ ） 【解】（1）过失.普遍从仅包罗二个已知轴力的结面启初. 习题5.2挖空(1)习题3.2(4)图所示桁架中有根整杆.习题3.2(4)图【解】（1）11（仅横背杆件中有轴力，其余均为整杆）. 习题5.3 试用结面法供图所示桁架杆件的轴力.(a) (b)【解】 (1)提示：根据整杆判别规则有：N13N430F F ==；根据等力杆判别规则有：N24N46F F =.而后分别对付结面2、3、5列力仄稳圆程，即可供解局部杆件的内力. (2) 提示：根据整杆判别规则有：N18N17N16N27N36N450F F F F F F ======；根据等力杆判别规则有：N12N23N34F F F ==；N78N76N65F F F ==.而后与结面4、5列力仄稳圆程，即可供解局部杆件的内力.习题5.4 推断图所示桁架结构的整杆.(a) (b) (c)【解】(a) (b) (c)提示：(c)题需先供出收座反力后，截与Ⅰ.Ⅰ截里以左为断绝体，由30M =∑，可得N120F =，而后再举止整杆推断. 习题5.5 用截里法供解图所示桁架指定杆件的轴力.(a)(b)【解】(1) N P 32a F F =-；N P 12b F F =；N Pc F F =提示：截与Ⅰ.Ⅰ截里可得到N b F 、N c F ；根据整杆推断规则，杆26、杆36为整杆，则通过截与Ⅱ.Ⅱ截里可得到N a F . (2)N 0a F =；N P b F =；N 0c F =提示：截与Ⅰ.Ⅰ截里可得到N b F ；由结面1可知N 0a F =；截与Ⅱ.Ⅱ截里，与圆圈以内为摆脱体，对付2面与矩，则N 0c F =.第6章 结构的位移估计习题解问习题6.1 利害推断题(1) 变形骸真功本理仅适用于弹性体系，不适用于非弹性体系.（ ）(2) 真功本理中的力状态战位移状态皆是真设的.（ ）(3) 功的互等定理仅适用于线弹性体系，不适用于非线弹性体系.（ ）(4) 反力互等定理仅适用于超静定结构，不适用于静定结构.（ ）(5) 对付于静定结构，有变形便一定有内力.（ ） (6) 对付于静定结构，有位移便一定有变形.（ ） (7) 习题4.1(7)图所示体系中各杆EA 相共，则二图中C 面的火仄位移相等.（ ）(8) M P 图，M 图如习题4.1(8)图所示，EI =常数.下列图乘截止是精确的：4)832(12l l ql EI ⨯⨯⨯ （ ）(9) M P 图、M (9)图所示，下列图乘截止是精确的：033202201111)(1y A EI y A y A EI ++ （ ）(10) (10)图所示结构的二个仄稳状态中，有一个为温度变更，此时功的互等定理不可坐.（ ） 习题 4.1(7)图习题 4.1(8)图 习题 4.1(9)图习题 4.1(10)图【解】（1）过失.变形骸真功本理适用于弹性战非弹性的所有体系.（2）过失.惟有一个状态是真设的. （3）精确.（4）过失.反力互等定理适用于线弹性的静定战超静定结构.（5）过失.譬如静定结构正在温度变更效率下，有变形但是不内力.（6）过失.譬如静定结构正在收座移动效率下，有位移但是稳定形.（7）精确.由桁架的位移估计公式可知.（8）过失.由于与0y 的M 图为合线图，应分段图乘.（9）精确. （10）精确.习题6.2挖空题(1) 习题4.2(1)图所示刚刚架，由于收座B 下重所引起D 面的火仄位移D H =______.(2) 真功本理有二种分歧的应用形式，即_______本理战_______本理.其中，用于供位移的是_______本理.(3) 用单位荷载法估计位移时，假制状态中所加的荷载应是与所供广义位移相映的________.(4) 图乘法的应用条件是：__________且M P 与M 图中起码有一个为直线图形.(5) 已知刚刚架正在荷载效率下的M P 图如习题4.2(5)图所示，直线为二次扔物线，横梁的抗直刚刚度为2EI ，横杆为EI ，则横梁中面K 的横背位移为________.(6) 习题4.2(6)图所示拱中推杆AB 比本安排少度短了，由此引起C 面的横背位移为________；引起收座A 的火仄反力为________.(7) 习题4.2(7)图所示结构，当C 面有F P =1(↓)效率时，D 面横背位移等于(↑)，当E 面有图示荷载效率时，C 面的横背位移为________.(8) 习题 4.2(8)图（a ）所示连绝梁收座B 的反力为)(1611R ↑=B F ，则该连绝梁正在收座B 下重B =1时（如图（b ）所示），D 面的横背位移Dδ=________.习题 4.2(1)图 习题 4.2(5)图习题 4.2(6)图 习题 4.2(7)图习题 4.2(8)图【解】（1）()3∆→.根据公式R ΔF c =-∑估计.（2）真位移、真力；真力 . （3）广义单位力.（4）EI 为常数的直线杆.（5）48.875()EI↓.先正在K 面加单位力并画M 图，而后利用图乘法公式估计.（6）1.5cm ↑；0.C 面的横背位移用公式NΔF l =∆∑估计；制制缺面不会引起静定结构爆收反力战内力.（7）()a∆↑.由位移互等定理可知，C 面效率单位力时，E面沿M 目标的位移为21a∆δ=-.则E 面效率单位力M =1时，C面爆收的位移为12a∆δ=-.（8）11()16↓.对付（a ）、（b ）二个图示状态，应用功的互等定理可得截止.C V .EI为常数.【解】1）供C V习题4.3(1)图（1） 积分法画M P 图，如习题4.3（1）(b)图所示.正在C 面加横背单位力F P =1，并画M 图如习题4.3（1）(c)图所示.由于该二个直矩图对付称，可估计一半，再将截止乘以2.AC 段直矩为12M x =，P P 12M F x =则（2） 图乘法 2)供C V习题4.3(2)图（1） 积分法画M P 图，如习题4.3（2）(b)图所示.正在C 面加横背单位力并画M 图，如习题4.3（2）(c)图所示.以C 面为坐标本面，x 轴背左为正，供得AC 段（0≤x ≤2）直矩为M x =，2P 10(2)M x =⨯+则（2） 图乘法由估计位移的图乘法公式，得3)供C V习题4.3(3)图（1） 积分法画M P 图，如习题4.3（3）(b)图所示.正在C 面加横背单位力并画M 图，如习题4.3（3）(c)图所示.根据图中的坐标系，二杆的直矩（按下侧受推供）分别为 AB 杆12M x =-，2P 142ql M x qx =-CB 杆M x =，P 2ql M x =则（2）图乘法 4)供A习题4.3（4）图（1）积分法画M P 图，如习题4.3（4）(b)图所示.正在A 面加单位力奇并画M 图，如习题4.3（4）(c)图所示.以A 为坐标本面，x 轴背左为正，直矩表白式（以下侧受推为正）为113M x l=-，2P 3122M qlx qx =-则358ql EI=（ ） （2） 图乘法由估计位移的图乘法公式，得358ql EI=（ ） 分别用积分法战图乘法供习题 4.4(a)图所示刚刚架C 面的火仄位移C H .已知EI =常数.【解】1）积分法P M 、M图分别如习题 4.4（b ）、（c ）图所示，修坐坐标系如（c ）图所示.各杆的直矩用x 表示，分别为 CD 杆M x =，P 12M qlx =AB 杆M x =，2P 12M qlx qx =-代进公式估计，得2）图乘法习题 4.5(a)图所示桁架各杆截里均为A =2×103m 2，E ×108kN/m 2，F P =30kN ，d =2m.试供C 面的横背位移V C ∆.D ql lBAC lA B lD CABD C22ql 2ql281ql 2(b)图M P M 图(c)(a)xx1ll【解】画NP F 图，如习题4.5(b)图所示.正在C 面加横背单位力，并画N F 图，如习题4.5(c)图所示. 由桁架的位移估计公式N NP F F Δl EA=∑，供得 第7章 力法习题解问利害推断题（1）习题5.1(1)图所示结构，当收座A 爆收转化时，各杆均爆收内力.（ ）习题5.1(1)图习题5.1(2)图（2）习题 5.1(2)图所示结构，当内中侧均降下t 1℃时，二杆均只爆收轴力.（ ）（3）习题 5.1(3)图(a)战(b)所示二结构的内力相共.（ ）习题5.1(3)图（4）习题 5.1(3)图(a)战(b)所示二结构的变形相共.（ ）【解】（1）过失.BC 部分是静定的附属部分，爆收刚刚体位移，而无内力.（2）过失.刚刚结面会沿左上圆爆收线位移，从而引起所连梁柱的蜿蜒.（3）精确.二结构中梁二跨的抗直刚刚度比值均为1:1，果此二结构内力相共.（4）过失.二结构内力相共，但是图(b)结构的刚刚度是图(a)的一倍，所以变形惟有图(a)的一半.习题7.2 挖空题（1）习题5.2(1) 图(a)所示超静定梁的收座A 爆收转角，若选图(b)所示力法基础结构，则力法圆程为_____________，代表的位移条件是______________，其中1c =_________；若选图(c)所示力法基础结构时，力法圆程为____________，代表的位移条件是______________，其中1c =_________.习题5.2(1)图（2）习题5.2(2)图(a)所示超静定结构，当基础体系为图(b)时，力法圆程为____________________，1P =________；当基础体系为图(c)时，力法圆程为____________________，1P =________.习题5.2(2)图（3）习题5.2(3)图(a)所示结构各杆刚刚度相共且为常数，AB 杆中面直矩为________，____侧受推；图(b)所示结构M BC =________，____侧受推.习题5.2(3)图（4）连绝梁受荷载效率时，其直矩图如习题5.2(4)图所示，则D 面的挠度为________，位移目标为____.习题5.2(4)图【解】（1）1111c 0X δ∆+=，沿X 1的横背位移等于整，－2l ；1111c X δ∆θ+=，沿X 1的转角等于，0.（2）11111P X X k δ∆+=-，458ql EI -；1111P 0X δ∆+=，3242ql q EI k+. （3）28ql ，下侧；2M ，下侧.可利用对付称性简化估计. （4）52EI，背下.选三跨简收梁动做基础结构，正在其上D 面加横背单位力并画M 图，图乘即可.试决定习题5.3图所示结构的超静定次数.图【领会】结构的超静定次数等于其估计自由度的千万于值，大概者使用“排除多余拘束法”直交领会.【解】（a ）1；（b ）2；（c ）5；（d ）3.用力法估计习题5.4图所示各超静定梁，并做出直矩图战剪力图.图【解】（1）本结构为1次超静定结构.采用基础体系如习题解5.4(1)图(a)所示，基础圆程为1111P 0X δ∆+=.系数战自由项分别为114EI δ=，1P 54EI∆=- 解得113.5kN m X =⋅.直矩图战剪力图分别如习题解5.4(1)图(d)战(e)所示. 习题解5.4(1)图用力法估计习题5.5图所示各超静定刚刚架，并做出内力图.图【解】（3）本结构为2次超静定结构.采用基础体系如习题解5.5(3)图(a)所示，基础圆程为系数战自由项分别为112503EI δ=，12210δδ==，226083EI δ=，1P 625EI ∆=，2P 20003EI∆= 解得17.5kN X =-，2 3.29kN X =-.内力图分别如习题解 5.5(3)图(e)~(g)所示. 习题解5.5(3)图利用对付称性，估计习题5.12图所示各结构的内力，并画直矩图.图【解】（2）将本结构所受普遍荷载领会为对付称战阻挡。

§3-2 多跨静定梁
例3-4 试作图a所示多跨静定梁的内力图，并求出各支座反力。
解：不算反力 先作弯矩图
1）绘AB、GH段弯矩图，与悬臂梁相同； 2）GE间无外力，弯矩图为直线，MF=0，可绘出； 同理可绘出CE段； 3）BC段弯矩图用叠加法画。
§3-2 多跨静定梁
由弯矩与剪力的微分关系画剪力图
由若干根梁用铰相联，并用若干支座与基础相联而组成的静定结构。
分析多跨静定梁的一般步骤
对如图所示的多跨静定梁，应先从附属部分CE开始分析：将 支座C 的支反力求出后，进行附属部分的内力分析、画内力图， 然后将支座 C 的反力反向加在基本部分AC 的C 端作为荷载，再 进行基本部分的内力分析和画内力图，将两部分的弯矩图和剪力 图分别相连即得整个梁的弯矩图和剪力图 。
弯矩图为直线：其斜率为剪力。图形从基线顺时针转，
剪力为正，反之为负。 弯矩图为曲线：根据杆端平衡条件求剪力，如图c。
剪力图作出后即可求支座反力 取如图e的隔离体可求支座 c— 的反力 弯矩—剪力 支座反力
§3-3 静定平面刚架
常见静定刚架的型式
悬臂刚 架
简支刚 架
三铰刚 架
§3-3 静定平面刚架
R FSR F E SD 8kN
FSR F 12kN
FSR B 0
§3-1 单跨静定梁
用截面法计算 控制截面弯矩。
MC 0
M A 20kN 1m 20kN m
M D 20kN 2m 58kN 1m 18kN m M E 20kN 3m 58kN 2m 30kN 1m 26kN m M F 12kN 2m 16kN m 10kN m 18kN m

第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。

2、按虚力原理所建立的虚功方程等价于几何方程。

3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。

4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.C.=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。

6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。

M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。

8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。

a a9、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。

二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。

q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。

EI = 常数 ，a = 2m 。

a a a 10kN/m12、求图示结构E 点的竖向位移。

EI = 常数 。

l l l /3 2 /3/3q13、图示结构，EI=常数 ，M =⋅90kN m , P = 30kN 。

求D 点的竖向位移。

P 3m 3m 3m14、求图示刚架B 端的竖向位移。

ql15、求图示刚架结点C 的转角和水平位移，EI = 常数 。

q16、求图示刚架中Ｄ点的竖向位移。

EI ＝常数。

l/217、求图示刚架横梁中Ｄ点的竖向位移。

EI＝常数。

18、求图示刚架中D点的竖向位移。

E I = 常数。

qll l/219、求图示结构Ａ、Ｂ两截面的相对转角，EI＝常数。

l/23l/320、求图示结构A、B两点的相对水平位移，E I = 常数。

ll21、求图示结构B点的竖向位移，EI = 常数。

返19回
§3—4 少求或不求反力绘制弯矩图
弯矩图的绘制，以后应用很广，它是本课最 重要的基本功之一。
静定刚架常常可少求或不求反力绘制弯矩图。
例如：1. 悬臂部分及简支梁部分，弯矩图可先绘出。
2. 充分利用弯矩图的形状特征(直线、零值)。
3.刚结点处的力矩平衡条件。
4. 用叠加法作弯矩图。
5. 平行于杆轴的力及外力偶产生的弯矩为常数。 6. 与杆轴重合的力不产生弯矩等。
满足投影平衡条件。
0 24kN C 0
22kN
24kN 22kN （返1b8 回）
例题 3—6 作三铰刚架的内力图
→HA VA↑ 26.7 20 6.7
解（：1）求反力
←HB
↑VB
由（∑2Y由）=V刚0A求VH作得架=AA杆=弯整1=30H体端矩0Bk8平4=弯图N6衡↑矩.，66，以，7kV∑D3NMB0C（=kBN杆1=→0o↑为k可←N例得↑）
M图: 通常检查刚结点处是否满足力矩的平衡条件。
例如取结点C为隔离体（图a），有：
∑MC=48－192+144=0 满足这一平衡条件。
48kN·m
C
192kN·m
Q(N)图：可取刚架任何一部分为隔
离体，检查∑X=0 和 ∑Y=0 是否满足。 144kN·m （a）
例如取结点C为隔离体（图b）， 有: ∑X=24－24=0 ∑Y=22－22=0
dQ q(x) dx
dM Q dx
d2M dx2
q(x)
据此，得直梁内力图的形状特征
梁上情况 q=0
q=常数
q↓ q↑
P 作用处
m 铰或
作用处 自由端 (无m）
水平线

4 静定刚架
本章小结
本章讨论静定刚架的计算，要点如下： （1）静定刚架的计算步骤 支座反力或约束力，各杆杆端内力，各杆的内力图，刚架 内力图 （2）支座反力的计算 悬臂刚架、简支刚架、三铰刚架（底铰等高或不等高）、 多层多跨静定刚架。 （3）刚架杆件截面内力有弯矩、剪力、轴力，注意正负号 规定。 （4）杆端截面内力的计算方法 刚架的刚结点处有交于该刚结点的各杆的不同的杆端截面 ，截面内力的计算方法是截面法。
（下边受拉）
1.5P
1.5Pa
Pa
B 0.5Pa
1.5P
0.5Pa
2P
1.5Pa
2P C 1.5P
2Pa
NCE 0,QCE 2P, MCE 2Pa
（右边受拉）
结构力学电子教程
4 静定刚架
4.13 计算题4-13图刚架结点D各杆截面内力。 解：
3kN/m C
2kN DE
NDC 4 3 4 16kN QDC 5.33kN
5kN/m
MB
YB 5kN()
A
1m B XB MB 0 : MB 1.5 0.8 51 0.5 0
YB MB 3.7kN m( )
结构力学电子教程
4.3
C
D
4 静定刚架
解：
4m
q
2kN/m a
2kN/m
qa
A
B
qa / 2
4.4
A
2kN 5kN
4m
a
10kN C
8kN D 4m
qa / 2
B
5m
YB 7.5kN( )
XB M B 0 : 2 5 2.5 YA 8 0
2.08kN
YA 2.5kN( )