功能原理 机械能守恒定律1
- 格式:ppt
- 大小:1.04 MB
- 文档页数:30



第四讲功能原理 机械能守恒定律 能量守恒定律k k k i i i i ii e E E E v m v m W W ∆=-=-=+∑122122)2121(系统的外力和内力作功的总和等于系统动能的增量。
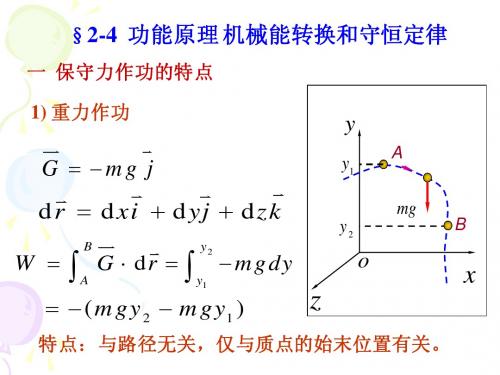
回顾前面学过的知识点:1. 质点系动能定理P1p 2p )(E E E W ∆-=--=2. 保守力作功等于势能的减少3. 成对力的功只与作用力和相对位移有关:r d F dW '⋅= 22/16※ 质点系功能原理1、系统的机械能: 动能与势能的总和称为机械能3、由势能的定义,保守内力的功总等于系统势能的减少pin c E W ∆-= 2、内力的功可分为: 保守内力的功和非保守内力功pk E E E +=(保守内力的功由势能代替)第四讲 功能原理 机械能守恒定律 能量守恒定律 in ncin c in in W W W W i i+==∑非保守内力的功将导致机械能与其他形式的能量转换。
inncex p k W W E E E +=∆+∆=∆k in ncp ex in nc in c ex in ex E W E W W W W W W ∆=+∆-=++=+ 4、系统的功能原理 (由质点系动能定理)在选定的质点系内,在任一过程中,质点系总机械能的增量等于所有外力的功与非保守内力的功的代数和。
4/16※ 机械能守恒定律问题1:有非保守内力作功,系统的机械能不守恒 ?例如:摩擦力作功,机械能转变成热能。
0=+in nc ex W W 0=∆+∆=∆p k E E E 常量=+p k E E 由功能原理:则:或:如果: 如果系统内只有保守内力作功,其他内力和一切外力都不作功,或元功之和恒为零,则系统内各物体的动能和势能可以相互转换,但总机械能保持不变。
问题2:有摩擦力作功:机械能守恒?in nc ex p k W W E E E +=∆+∆=∆力 f 作正功,f ' 作负功,总和为零,机械能守恒。


机械能守恒定律的应用与功能原理主要内容:一、机械能守恒定律1)在机械运动范围内,物体所具有的动能、势能(重力势能和弹性势能),统称为机械能。
物体的动能和势能之间是可以相互转化的。
例如:自由下落的物体,由于重力做功,所以其势能减少,动能增加,势能转化为动能;竖直上抛的物体,由于要克服重力做功,所以其动能减少,势能增加,动能转化为势能。
下面从动能定理出发,推证机械能守恒的条件:选某物体为研究对象,根据动能定理,有:ΣW=ΔE k可写成:W重+W弹+W其它=ΔE k,其中W弹为弹簧弹力的功。
又根据重力、弹簧弹力做功与势能的关系有:W重=-ΔE P重,W弹=-ΔE P弹-ΔE P重-ΔE P弹+W其它=ΔE k,如果W其它=0,即其它力不做功,则:-ΔE P重-ΔE P弹=ΔE k,即ΔE k+ΔE P重+ΔE P弹=0即ΔE=0 (机械能的增量为零)从上面推证可以看出,系统机械能守恒的条件为:除了重力、弹簧弹力以外无其它力对物体做功。
2)实际上,物质运动的形式不仅是机械运动,另外,热运动、电磁运动、化学运动、核运动等也是物质的不同运动形式,不同的运动形式对应着不同形式的能量,物质各种形式的运动是可以相互转化的,因此不同形式的能也是可以相互转化的,且在能量转化的过程中,总的能量守恒。
因此,系统机械能守恒条件的严格表述为:物体系(系统)内只有重力、弹力做功,而其它一切力都不做功时,系统机械能守恒。
二、功能原理(或称功能关系)1)由动能定理可以知道,外力对物体做功的代数和等于物体动能的增量,可表示为:ΣW=ΔE k 这里说的外力包括作用于物体上的全部做功的力,可分为三部分:(1)系统内的重力、弹力;(2)系统内的摩擦力;(3)系统外物体对它的作用力,则动能定理的表达式可写成W重+W弹+W摩擦+W外=ΔE k,又因为:W重=-ΔE P重,W弹=-ΔE P弹,所以有:W摩擦+W外=ΔE k+ΔE P重+ΔE P弹等式的右边为动能的增量跟势能增量的和,即为物体机械能的增量,即:W摩擦+W外=ΔE表述为:除重力、弹簧弹力以外力对物体做功的代数和,等于物体机械能的增量。