(完整版)第六章弹性波波动方程及其解

格式：ppt
大小：2.20 MB
文档页数：12

下载文档原格式

基础物理学上册习题解答和分析第六章习题解答和分析

习题六6-1频率为Hz 41025.1⨯=ν的平面简谐纵波沿细长的金属棒传播，棒的弹性模量211/1090.1m N E ⨯=，棒的密度33/106.7m Kg ⨯=ρ.求该纵波的波长. 分析纵波在固体中传播，波速由弹性模量与密度决定。

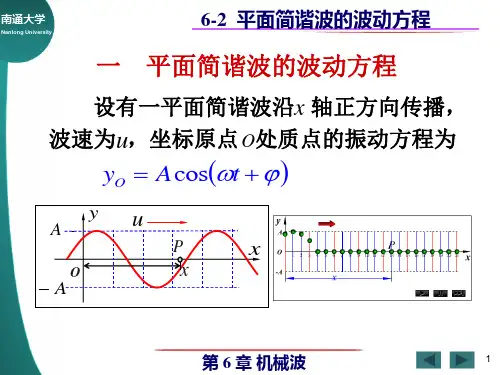
解：波速ρ/E u =,波长νλ/u = 2/0.4E m λρν==6-2一横波在沿绳子传播时的波方程为：))(5.2cos(04.0SI x t y ππ-=(1)求波的振幅、波速、频率及波长；(2)求绳上的质点振动时的最大速度；(3)分别画出t=1s 和t=2s 的波形，并指出波峰和波谷.画出x=1.0m 处的质点的振动曲线并讨论其与波形图的不同.解：（1）用比较法，由)2cos()5.2cos(04.0x t A x t y λπϕωππ-+=-=得0.04A m = ； /2 2.5/2 1.25Hz νωπππ===；2, 2.0m ππλλ== 2.5/u m s λν==（2）0.314/m A m s νω==（3）t=1(s)时波形方程为：)5.2cos(04.01x y ππ-= t=2(s)时波形方程为：)5cos(04.02x y ππ-=x=1(m)处的振动方程为：)5.2cos(04.0ππ-=t y6-3 一简谐波沿x 轴正方向传播，t=T/4时的波形图如题图6－3所示虚线，若各点的振动以余弦函数表示，且各点的振动初相取值区间为（-π，π].求各点的初相.分析由t=T/4时的波形图(图中虚线)和波的传播方向,作出t=0时的波形图。

依旋转矢量法可求t=0时的各点的相位。

解:由t=T/4时的波形图(图中虚线)和波的传播方向,作出t=0时的波形图(图中实线),依旋转矢量法可知质点1的初相为π; 质点2的初相为π/2; 质点3的初相为0; 质点4的初相为-π/2.6-4 有一平面谐波在空间传播,如题图6－4所示.已知A 点的振动规律为)t cos(A y ϕ+ω=，就图中给出的四种坐标,分别写出它们波的表达式.并说明这四个表达式中在描写距A 点为b 处的质点的振动规律是否一样? 分析无论何种情况，只需求出任意点x 与已知点的相位差，同时结合相对坐标的传播方向（只考虑相对于题图题图6-3t=坐标方向的正负关系）即可求解波的表达。

大学物理波动方程

4
波线: 沿波的传播方向作的有方向的线。波前: 在某一时刻，波传播到的最前面的波面。
波面波线
波面
波线
球面波 z
波面
x
y
波线
平面波
柱面波
5
注意在各向同性均匀介质中，波线⊥波面。
三、波长
周期
频率和波速
波长（） : 同一波线上相邻两个相位差为 2 的质点之间
的距离；即波源作一次完全振动，波前进的距离。波长反映了波的空间周期性。
T 4s
2m
u 0.5 m s 1
2 rad s 1 T 2 y0 0.5 cos( t ) t=0原点0: 2 2 2
20
例一平面简谐波沿x轴正方向传播，已知其波函数为
y 0.04 cos (50t 0.10 x) m
1
横波波的传播方向质点的振动方向特点：具有波峰和波谷纵波波的传播方向质点振动方向特点：具有疏密相间的区域
下面以横波为例观察波的形成过程
2
t 0
1 2
3
4
5
6
7
8
9 10 11 12 13
静止
T t 4
1 2
3
4
5
6
7
8
9 10 11 12 13
振动状态传至4
T t 2
1 2
t1 时刻x1 处的振动状态经Δt 时间传播到x1+Δx 处，则
可得到
x1 x1 x (t1 ) (t1 t ) u u x u t
x y ( x, t ) A cos[ (t ) 0 ] u x y ( x, t ) A cos[2π (t ) 0 ] t x y ( x, t ) A cos[2π ( ) 0 ] T

波动方程和能量详解

波的干涉是在特定条件下波叠加所产生的现象能够产生干涉现象的波，称为相干波。激发相干波的波源，称为相干波源。
32
4. 相干条件
（1）频率相同：若两列波的频率不同，则两者的相位差随时间变化，合振动的振幅也随时间变化，因而不可能观察到稳定的结果；
y1A1cos(1t2x11)
y2A2cos(2t2x22)
•解的形式：
综量是 x ut 的函数
介质中的波速
f x ut
当然包括 y Acos t kx 平面简谐波
由
y(x,t)
A cos[ (t
x) u
0 )]
知
2 y t2
A
2
cos[ (t
x) u
0]
2 y x2
A
2
u2
cos[ (t
x) u
0 ]
2 y x2
1 u2
2 y t2
xA0cos4t
半径为10m的波面上，某点a 的振动方程为：
x12cos4(t18)
(1)求此波的波长；
(2)求半径为25m的球形波面上任一点b 的振幅和振动方程。
解： (1) 球面波的波动方程为 x(r,t)Acos[(tr)]
r
u
又 r 10m
x 1 (t) 1 A 0c o s (t 1 u 0 ) 2 c o s4 (t 8 1 )
平衡位置时的总能量： E Emax
最大位置时的总能量：
E 0
12
2. 还有一点需要指出的，这就是势能属于谁的问题。在波动中介质体元的势能是由介质体元自身的形变引起的，所以这份势能就应该属于形变体元自身所具有。形变体元实际上已经包含了相互作用着的各个物体，或者说，形变体元自身就是一个由相互作用的物体所组成的系统 .

第六章_波动方程

一、波动方程
7.2.3 一维势垒的简单讨论粒子在I区，具有能量E>0。各区的势垒如下，求粒子在各区出现的几率。
0 (0<x<x1) [I区] V＝
V2>E (x1<x<x2) [II区]
0 (x>x2) [III区]
一、波动方程列出此问题的薛定谔方程：
2 d 2u V x u Eu 2 2m dx d 2u 2m 2 V E u 2 dx
此方程比较难解，令 x,
2
2
(1)
mk 2
4
那么
d 2u 2mE mk 2 2 2 2 4 u 0 2 d
(2)
一、波动方程令括号内第二项的常数部分为1，用λ代替括号内第一项，那么 2化简为：
d 2u 2 u 0, 2 d
波动方程
一、波动方程
第七章波动方程
波动方程（wave equation）是一种重要的偏微分方程，主要描述自然界中的各种的波动现象，例如声波，光波和水波。波动方程抽象自声学，电磁学，和流体力学等领域。
历史上许多科学家，如达朗贝尔、欧拉、丹尼尔²伯努利和拉格朗日等在研究乐器等物体中的弦振动问题时，都对波动方程理论作出过重要贡献。
px i x
所以动量px可以用算符 i 来表示。同理有 x
p y i y
pz i z
一、波动方程
那么
p p p p 2 2 2 x y z 2 2
2 2 2 2 2 x 2 y 2 z 2
波函数两边取对t的偏导
i E , t

波动方程举例ppt课件

500 Hz
0.02 s 0.4 m
精品课件
15
2. x = 2 m 处
0.05 cos ( 5×2 – 100 t ) 0.05 cos ( 100 t –10 ) 初相为–10
3. x1 = 0.2 m 处的振动相位比原点处的振动相位落后
x2 = 0.35 m 处的振动相位比原点处的振动相位落后
解：1.
0.05 cos ( 5 x – 100 t ) 0.05 cos 100 ( t – x )
20
cosa = cosa
正向波
精品课件
14
波动方程 y = 0.05 cos ( 5 x – 100 t ) (SI)
与
y
Acos(t
x u
)
比较得 0.05 m
100
20 m ·s -1
0. 02 8
精品课件
18
（2）p点处x = 0.2m,代入上述波动方程
y0.c 0o 4 0s .[ 4t0. 2 -]
0. 02 8
0.0c4o0s.[4t]
2
方法二设波动方程为
y
Acos(t
x u
)
A=0.04m
u=0.08m/s
2 0.4
T
？
把x=0代入上述波动方程 y Acost
31 02co4sπ[t3π] 5
精品课件
9
u
8m 5m 9m
C
B oA
Dx
点 D 的相位落后于点 A
D
A
-
x u
4t - 4 9
20
yD31 0 2co4sπt[-5 9]
31 02co4sπ[t]

弹性波动理论详解

图1.6 波前、波后和射线
菲涅尔补充：由波前面上各点所产生的子波，在观测点上相互干涉叠加，其叠加结果就是我们在该点观测到的总振动。惠更斯—菲涅尔原理（又称波前原理）：既可用于均匀介质，也可用于非均匀介质，利用这个原理可以构制反射界面、折射界面等。 2.费马原理弹性波的传播，除了可用波前来描述外，还可用射线来描述：射线：波从空间一点到另一点的传播路径。在任一点上，射线总是垂直于波前。
垂直面内分量：称SV波
从波动方程知：纵、横波传播速度为
Vp
1 (1 )(1 2 ) E 1 Vs 2 (1 ) E
( 2 )

(1.15)
则纵、横波速度之比为
Vp Vs 1 0 .5
(1.16) 表1.2 Vp/Vs值与介质泊松比的关系
(2) 泊松比（σ）在拉伸形变中，直杆的横切面会减小。反之，在轴向挤压时，横截面将增大。也就是说，在拉伸或压缩形变中，纵向增量 L和横向增量 d的符号总是相反的。泊松比: 介质的横向应变与纵向应变的比值
σ =- L / L
(3) 体变模量
d / d
(1.6)
一个体积为V的立方体，在流体静压力P的挤压下所发生体积形变。即每个正截面的压体变模量（压缩模量）: 压力P与体积相对变化之比 P (1.7) K=-
解决某些特殊问题，如探测充满液体的洞穴（如溶洞）, Vs=0
体波：纵、横波，在整个空间面波：弹性分界面附近瑞利面波：自由界面，地滚波，R波特点：低频、低速，能量大（强振幅），旋转（铅垂面，椭圆，逆转）天然地震中，危害极大勒夫面波：低速带顶底界面，平行界面的波动，振动方向垂直传播方向， SH波特点：对纵波勘探影响不大，对横波勘探严重干扰

第六章弹性波波动方程及其解ppt课件

又 • u • uS 0

2

代入纳维方程 ( )( • u ) u f u

uS f uS

2 2
VS uS f uS
2

vs

结论：在均匀各向同性弹性体内，切变扰动以速度VS向
(4)
(5)
式u j , ji (ui , jj u j ,ij ) f i ui即为位移在弹性体
内传播时所满足的方程 .称为纳维 ( Navier)方程.
纳维方程是线性弹性假设条件下得到的各向同性弹性体中
的弹性波最基本方程。
指标表示的纳维方程 ( )u j , ji ui , jj f i ui
§6.1 线性弹性动力学的基本方程
1.
基本方程
➢
➢
运动微分方程 ji , j
几何方程
1
eij (ui , j u j ,i )
2
2 ui
f i 2
t
u1
e11
x1
u2
e22
x2
u
e33 3
x3
1 u1 u2
e12 (

)
2 x2 x1
v p t
上式表示波场是以速度VP向外传播的无旋场。

转动矢量表示的横波方程

2
( )( • u ) u f u两边取旋度

2

(

u
)
( )( ( • u )) 2 ( u ) ( f )

弹性波

2 E 1 e ( 2 ) 2 t 2 (1 ) 1 2 y
2 E 1 e ( 2w) 2 t 2 (1 ) 1 2 z
一、无旋波所谓无旋波是指在弹性体中，波动所产生的变形不存在旋转，即弹性体在任一点对三个垂直坐标轴的旋转量皆为零。假定弹性体的位移 u,v,w 可以表示成为：
纵波波动方程的通解是：
u( x, t ) f1 ( x c1t ) f 2 ( x c1t )
二、横波 [定义] 弹性体的质点运动方向垂直于弹性波的传播方向。
横波的传播形式
由于横波的体积应变 e=0，故横波为等容波。
这就是按位移求解动力问题的基本微分方程，也称为拉密（Lame) 方程。要求解拉密方程，显然需要边界条件。除此之外，由于位移分量还是时间变量的函数，因此求解动力问题还要给出初始条件。为求解上的简便，通常不计体力，此时弹性体的运动微分方程简化为：
2u E 1 e ( 2u ) 2 t 2 (1 ) 1 2 x
z
1 [ z ( x y )] E
1 E
xy
2 (1 ) xy E
由于位移分量很难用应力及其导数来表示，所以弹性力学动力问题通常要按位移求解。将应力分量用位移分量表示的弹性方程代入运动微分方程，并令：
e
得到：
u w x y z
弹性波
概述：当静力平衡状态下的弹性体受到荷载作用时，并不是在弹性体的所有各部分都立即引起位移、形变和应力。在作用开始时，距荷载作用处较远的部分仍保持不受干扰。在作用开始后，荷载所引起的位移、形变和应力，就以波动的形式用有限大的速度向别处传播。这种波动就称为弹性波。本章将首先给出描述弹性体运动的基本微分方程，然后介绍弹性波的几个概念，针对不同的弹性波，对运动微分方程进行简化，最后给出波在无限大弹性体中传播速度公式。本章仍然采用如下假设：（1）弹性体为理想弹性体。（2）假定位移和形变都是微小的。上述两条假设，完全等同于讨论静力问题的基本假设。因此，在静力问题中给出的物理方程和几何方程，以及把应力分量用位移分量表示的弹性方程，仍然适用于讨论动力问题的任一瞬时，所不同的仅仅在于，静力问题中的平衡微分方程必须用运动微分方程来代替。对于任取的微元体，运用达朗伯尔原理，除了考虑应力和体力以外，还须考虑弹性体由于具有加速度而产生的惯性力。每单位体积上的惯性力在空间直角坐标系的 x,y,z 方向的分量分别为:

波动方程ppt课件

＝
2π
2π
d ＝Cd
C (本题结束)
判断各点运动方向的技巧
上坡下行
例题：有一列横波向右
下坡上行
传播，画出波形曲线上 A、B 、C 、D 、E 、F 各点的运动方向和四分之
y C· B· ·D
u
一周期后的波形曲线。
· A 0
T 4
E·
·F
x
特别要注意：波的传播方向，这是关键。
例题：图（a）中所表示的x ＝0 处质点振动的初相位
y(m) 0.04
0
－0.04
u＝0.08 m/s
.a
b.
0.2
0.4
x (m)
例题：一列沿x 正向传播的简谐波，已知t1=0和
t2=0.25s时的波形如图。
试求：（1）振动方程（2）波动方程（3）作出波源振动曲线。
（练习册P32计算题3·版书）
y(m)
u
0.02m
t1 t2
..
.
0
P
x (m)
置的位移（坐标为 y）随时间t 的变化关系。
波波
函数
动方程
y
=A
cos ω
(
t－
x
u
)
+j
波向x 轴正方向传播也称右行波
波向x 轴负方向传播也称左行波
y
=A
cos
ω
(
t
＋
x
u
) +j
物理意义：波线上任一点（距原点为 x）处的质点任一瞬间相对其平衡位置的位移。
当波向x 轴正方向传播而且已知距离0点为xo的Q点振动方程为：
与图（b）所表示的振动的初相位分别为：

弹性波波长计算公式_固体中的弹性波

弹性波波长计算公式_固体中的弹性波[拼⾳]：guti zhong de tanxingbo[外⽂]：elastic waves in solids也叫固体中的应⼒波。

它是固体中的⼀种机械波动，把固体中某⼀点或部分受⼒或其他原因的扰动引起的形变，如体积形变或剪切形变，以波动的形式传播到固体的其他部分。

在波动传播过程中，固体中的质点除在它原来的位置上有微⼩的振动外，并不产⽣永久性的位移。

因为固体有弹性，弹性⼒有使扰动引起的形变恢复到⽆形变的状态的能⼒，于是形成波动。

弹性是固体中能形成波动的主要原因。

在各向同性⽆限⼤的固体中，可以有两种类型的弹性波。

⼀种是纵波，另⼀种是横波。

在各向同性⽆限⼤的固体中，纵波传播速度为(1)式中с1是固体中纵波的传播速度，单位为m/s，ρ是固体媒质的密度，单位为kg/m3，μ┡和μ是有量纲的常数，常称为拉梅常数，μ也称为切变模量或切变弹性系数，E是弹性模量，σ 是泊松⽐。

纵波在固体媒质中传播时，常使固体的体积有交替的压缩和膨胀，因此纵波⼜叫膨胀波。

横波在固体中传播的速度是(2)式中сt是横波传播速度。

横波在固体中传播时不引起体积变化。

横波⼜称为切变波或旋转波。

地震时在地壳中常引起纵波和横波，即所谓P 波和S波。

因为纵波速度с1⼤于横波速度сt，所以地震时P波⽐S波早到远离震源的观测点。

在各向同性半⽆限的固体中，或⼀种固体与另⼀种固体的分界⾯处，波动⼊射在分界⾯上时除产⽣反射波和折射波外，还会引起波型的转换，如图1所⽰。

AB代表两种不同固体的分界⾯，NON┡为AB平⾯上的法线，如CO表⽰⼊射到AB平⾯上O点的平⾯纵波的波束，除在分界⾯处反射和折射⽽形成的反射纵波OD和折射纵波OF外，还转换成反射横波OE和折射横波OG。

⼊射⾓i、反射⾓γ和α、折射⾓β和γ的⼤⼩，与固体1和固体2中的波速有关，可⽤斯涅⽿定律(3)求出。

式中с11和с12是固体1和固体2中的纵波速度，сt1和с掯是固体1和固体2中横波速度。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。