下载文档原格式
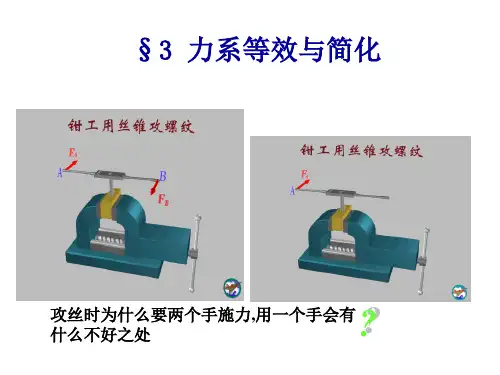
第三章 力系的简化和平衡引言力系分为：空间一般力系（空间汇交系、空间平行力系）和平面一般力系（平面汇交力系、平面平行力系）。
研究物体受力情况→作用在物体上的一组复杂力系→简化及合成→平衡条件研究。
§3.1 力线平移定理力线的平移定理：作用在刚体上O 点的力F 可平移到任意O '点，但必须附加上一个相应的力偶(称附加力偶)，这个附加力偶矩失等于原来的力F 对新作用点O '和矩。
且()d F F M M O ⋅==' (d 是力偶臂)力线平移定理不仅是力系简化的依据，也是分析力所物体效应的一个重要方法。
注：力线平移定理只能适应于静定刚体 证明：如F 图所示a. 力F 作用于刚体上O 点；b. 在刚上'O 处加上一对平衡力(F F ''',)，且F F F ''-='=。
根据加减平衡力系原理：（F F F ''',,）中（F F '',）等值反向不共线，是一对力偶, 这个力偶称为附加力偶。
附加力偶距失()F M d F M O '=⋅=ba§3.2 力系的简化、主矢与主矩一、力系的简化在工程中，最常见的力系是不同一平面内，不完全相交，也不完全平行的空间的一般力系。
在对作用于物体的力系的研究过程当中，首先将力系向任意一点进行简化。
如图所示：空间力系(1F ,2F ,…n F )，O 点为任取的简化中心1) 根据力线平移定理，将力系中各力1F ,2F ,…m F 平移到O 点→作用于O 点的空间汇力系(1'F ,2'F ,…n F ')及附加力偶系(1M ,2M ,…n M )11'F F =，22'F F =,… n n F F '=()11F M M O = ()22F M M O =…()n O n F M M =2) 将以上两个力系分别合成F F F F F F F R n n ∑=+++=+++=' 2121 n O M M M M +++= 21()()()()i O n O O O F M F M F M F M ∑=+++= 21R ':原力系主矢，是空间一般力系中各力的矢量和，与简化中心无关。
第三章 力系的简化和平衡引言一、力系分类1.汇交力系: 空间平行力系和平面汇交力系。
2. 一般力系：平面一般力系、空间一般力系。
3.平行力系。
平面平行力系和空间平行力系。
二、物体受力计算路径研究物体受力情况→作用在物体上的一组复杂力系→简化及合成→物体受力结果。
§3.1 力线平移定理力线的平移定理：作用在刚体上O 点的力F 可平移到任意O '点，但必须附加上一个相应的力偶(称附加力偶)，这个附加力偶矩失等于原来的力F 对新作用点O '和矩。
且()d F F MM O ⋅=='(d 是力偶臂)力线平移定理不仅是力系简化的依据，也是分析力所物体效应的一个重要方法。
注：力线平移定理只能适应于静定刚体 证明：如F 图所示图中：力F 作用于刚体上O 点；在刚上'O 处加上一对平衡力(F F ''',)，且F F F ''-='=。
根据加减平衡力系原理：（F F F ''',,），中（F F '',）等值反向不共线，是一对力偶, 这个力偶称为附加力偶。
附加力偶距失()F M d F M O '=⋅=。
b()ac§3.2 力系的简化、主矢与主矩一、力系的简化在工程中，最常见的力系是不同一平面内，不完全相交，也不完全平行的空间的一般力系。
在对作用于物体的力系的研究过程当中，首先将力系向任意一点进行简化。
如图所示：空间力系(1F ,2F ,…n F )，O 点为任取的简化中心1. 根据力线平移定理，将力系中各力1F ,2F ,…m F 平移到O 点→作用于O 点的空间汇力系(1'F ,2'F ,…n F ')及附加力偶系(1M ,2M ,…n M )11'F F =，22'F F =,… nn F F '=()11F M M O= ()22F MMO=…()n OnF MM=2.将以上两个力系分别合成F F F F F F F R n n ∑=+++=+++=' 2121nO MM M M+++= 21()()()()i O n O O OF M F M F M F M∑=+++=21R ':原力系主矢，是空间一般力系中各力的矢量和，与简化中的无关。
第2章 力系的等效与简化2.1 力系等效与简化的概念2.1.1 力系的主矢与主矩主矢的概念： 由若干多个力所组成的力系12(,,,)n F F F ⋅⋅⋅中所有力的矢量和，称为力系的主矢量，简称为主矢，用R F 表示，即1nR ii F F ==∑注意：主矢只有大小和方向，未涉及作用点。
对一个确定的力系主矢是唯一的。
主矩的概念： 力系中所有力对同一点之矩的矢量和，称为力系对这一点的主矩，用O M 表示，即1()nO O i i M M F ==∑注意：主矩是对某一确定点的。
同一力系对不同的点其主矩一般不同。
12O O M M ≠2.1.2 等效的概念设有两力系12(,,,)n F F F ⋅⋅⋅和12(,,,)n F F F '''⋅⋅⋅。
1nR ii F F ==∑，1nR i i F F =''=∑1()nO O i i M M F ==∑，1()nOO i i M M F ='''=∑。
等效力系：如果两力系的主矢和对同一点的主矩分别对应相等，二者对同一刚体就会产生相同的运动效应，则称则两个力系为等效力系。
2.1.3 简化的概念力系的简化：将由若干个力和力偶所组成的力系，变为一个力或一个力偶或者一个力和一个力偶等简单而等效的情形。
这一过程就称为力系的简化。
2.2 力偶及其性质2.2.1 力偶-----最简单、最基本的力系 1、力偶的概念 工程实例：方向盘搅拌器丝锥力偶：两个大小相等，作用线不重合的反向平行力组成的力系。
记为),(F F '。
F F '-=F F '=力偶臂：力偶中两力之间的垂直距离h ，称为力偶臂。
力偶的作用面：力偶所在的平面。
2、 力偶矩力偶使物体产生绕某点转动的效应。
F F '-=()()()O O A BA B AB M M F M F F r F r r r F r F''=+=⨯+⨯=-⨯=⨯若任意另取一点仍有AB M r F =⨯。
