土木工程力学教案——力系的等效与简化
- 格式:doc
- 大小:405.00 KB
- 文档页数:9





第五讲内容第二章力系的等效与简化一、刚体和平衡的概念刚体:在受力作用后而不产生变形的物体称为,刚体是对实际物体经过科学的抽象和简化而得到的一种理想模型。
而当变形在所研究的问题中成为主要因素时(如在材料力学中研究变形杆件),一般就不能再把物体看作是刚体了。
平衡:指物体相对于地球保持静止或作匀速直线运动的状态。
显然,平衡是机械运动的特殊形态,因为静止是暂时的、相对的,而运动才是永衡的、绝对的。
二、力系、等效力系、平衡力系力系:作用在物体上的一组力。
按照力系中各力作用线分布的不同形式,力系可分为:(1)汇交力系力系中各力作用线汇交于一点;(2)力偶系力系中各力可以组成若干力偶或力系由若干力偶组成;(3)平行力系力系中各力作用线相互平行;(4)一般力系力系中各力作用线既不完全交于一点,也不完全相互平行。
按照各力作用线是否位于同一平面内,上述力系各自又可以分为平面力系和空间力系两大类,如平面汇交力系、空间一般力系等等。
等效力系:两个力系对物体的作用效应相同,则称这两个力系互为等效力系。
当一个力与一个力系等效时,则称该力为力系的合力;而该力系中的每一个力称为其合力的分力。
把力系中的各个分力代换成合力的过程,称为力系的合成;反过来,把合力代换成若干分力的过程,称为力的分解。
平衡力系:若刚体在某力系作用下保持平衡。
在平衡力系中,各力相互平衡,或者说,诸力对刚体产生的运动效应相互抵消。
可见,平衡力系是对刚体作用效应等于零的力系。
第一节静力学基本公理静力学公理是人们从实践中总结得出的最基本的力学规律,这些规律的正确性已为实践反复证明,是符合客观实际的。
一、二力平衡公理作用于刚体上的两个力平衡的充分与必要条件是这两个力大小相等、方向相反、作用线相同。
这一结论是显而易见的。
如图所示直杆,在杆的两端施加一对大小相等的拉力(F1、F2)或压力(F2、F1),均可使杆平衡。
图2-1应当指出,该条件对于刚体来说是充分而且必要的;而对于变形体,该条件只是必要的而不充分。



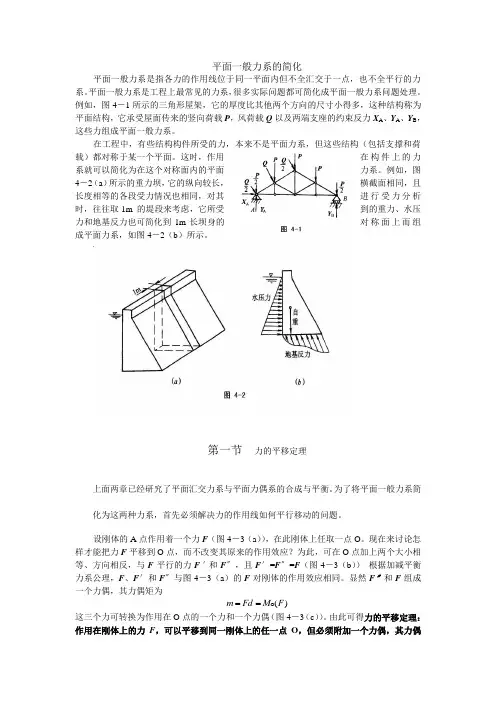
平面一般力系的简化平面一般力系是指各力的作用线位于同一平面内但不全汇交于一点,也不全平行的力系。
平面一般力系是工程上最常见的力系,很多实际问题都可简化成平面一般力系问题处理。
例如,图4-1所示的三角形屋架,它的厚度比其他两个方向的尺寸小得多,这种结构称为平面结构,它承受屋面传来的竖向荷载P,风荷载Q以及两端支座的约束反力X A、Y A、Y B,这些力组成平面一般力系。
在工程中,有些结构构件所受的力,本来不是平面力系,但这些结构(包括支撑和荷载)都对称于某一个平面。
这时,作用在构件上的力系就可以简化为在这个对称面内的平面力系。
例如,图4-2(a)所示的重力坝,它的纵向较长,横截面相同,且长度相等的各段受力情况也相同,对其进行受力分析时,往往取1m 的堤段来考虑,它所受到的重力、水压力和地基反力也可简化到1m长坝身的对称面上而组成平面力系,如图4-2(b)所示。
第一节力的平移定理上面两章已经研究了平面汇交力系与平面力偶系的合成与平衡。
为了将平面一般力系简化为这两种力系,首先必须解决力的作用线如何平行移动的问题。
设刚体的A点作用着一个力F(图4-3(a)),在此刚体上任取一点O。
现在来讨论怎样才能把力F平移到O点,而不改变其原来的作用效应?为此,可在O点加上两个大小相等、方向相反,与F平行的力F′和F〞,且F′=F〞=F(图4-3(b))根据加减平衡力系公理,F、F′和F〞与图4-3(a)的F对刚体的作用效应相同。
显然F〞和F组成一个力偶,其力偶矩为m=Fd=)M(O F这三个力可转换为作用在O点的一个力和一个力偶(图4-3(c))。
由此可得力的平移定理:作用在刚体上的力F,可以平移到同一刚体上的任一点O,但必须附加一个力偶,其力偶矩等于力F 对新作用点O 之矩。
顺便指出,根据上述力的平移的逆过程,共面的一个力和一个力偶总可以合成为一个力,该力的大小和方向与原力相同,作用线间的垂直距离为 F m d '= 力的平移定理是一般力系向一点简化的理论依据,也是分析力对物体作用效应的一个重要方法。

第2章 力系的等效与简化 作用在实际物体上的力系各式各样,但是,都可用归纳为两大类:一类是力系中的所有力的作用线都位于同一平面内,这类力系称为平面力系;另一类是力系中的所有力的作用线位于不同的平面内,称为空间力系。
这两类力系对物体所产生的运动效应是不同的。
同一类力系,虽然其中所包含的力不会相同,却可能对同一物体产生相同的作用效应。
在就是前一章中提到的力系等效的概念。
本章将在物理学的基础上,对力系的基本特征量加以扩展,引入力系主矢与主矩的概念;以此为基础,导出力系等效定理;进而应用力向一点平移定理以及力偶的概念对力系进行简化。
力系简化理论与方法将作为分析所有静力学和动力学问题的基础。
§2-1 力系等效定理 2-1-1 力系的主矢和主矩 2-1-2 力系等效定理 §2-2 力偶与力偶系 2-2-1 力偶与力偶系 2-2-2 力偶的性质 2-2-3 力偶系的合成 §2-3 力系的简化 2-3-1 力向一点平移定理 2-3-2 空间一般力系的简化 2-3-3 力系简化在固定端约束力分析中的应用 §2-4 结论和讨论 2-4-1 关于力矢、主矢、力矩矢、力偶矩矢以及 主矩矢的矢量性质 2-4-2 关于合力之矩定理及其应用 2-4-3 关于力系简化的最后结果 2-4-4 关于实际约束的简化模型 2-4-5 关于力偶性质推论的应用限制 习 题 本章正文 返回总目录第2章 力系的等效与简化 §2-1 力系等效定理 物理学中,关于质点系运动特征量已有明确论述,这就是:质点系的线动量和对某一点的角动量。
物理学中还指明线动量对时间的变化率等于作用在质点系上的合外力;角动量对时间的变化率等于作用在质点系上外力对同一点的合力矩。
这里的合外力,实际上只有大小和方向,并未涉及作用点或作用线。
因而,需要将其中的合外力与外力的合力矩扩展为力系的主矢和主矩。
2-1-1 力系的主矢和主矩 主矢:一般力系(F 1,F 2,…,F n )中所有力的矢量和(图2—1),称为力系的主矢量,简称为主矢(principal vector ),即∑=ni i1R FF =(2-1)图2-1力系的主矢其中F R 为力系主矢;F i 为力系中的各个力。
第2章 力系的等效与简化2.1 力系等效与简化的概念2.1.1 力系的主矢与主矩主矢的概念: 由若干多个力所组成的力系12(,,,)n F F F ⋅⋅⋅中所有力的矢量和,称为力系的主矢量,简称为主矢,用R F 表示,即1nR ii F F ==∑注意:主矢只有大小和方向,未涉及作用点。
对一个确定的力系主矢是唯一的。
主矩的概念: 力系中所有力对同一点之矩的矢量和,称为力系对这一点的主矩,用O M 表示,即1()nO O i i M M F ==∑注意:主矩是对某一确定点的。
同一力系对不同的点其主矩一般不同。
12O O M M ≠2.1.2 等效的概念设有两力系12(,,,)n F F F ⋅⋅⋅和12(,,,)n F F F '''⋅⋅⋅。
1nR ii F F ==∑,1nR i i F F =''=∑1()nO O i i M M F ==∑,1()nOO i i M M F ='''=∑。
等效力系:如果两力系的主矢和对同一点的主矩分别对应相等,二者对同一刚体就会产生相同的运动效应,则称则两个力系为等效力系。
2.1.3 简化的概念力系的简化:将由若干个力和力偶所组成的力系,变为一个力或一个力偶或者一个力和一个力偶等简单而等效的情形。
这一过程就称为力系的简化。
2.2 力偶及其性质2.2.1 力偶-----最简单、最基本的力系 1、力偶的概念 工程实例:方向盘搅拌器丝锥力偶:两个大小相等,作用线不重合的反向平行力组成的力系。
记为),(F F '。
F F '-=F F '=力偶臂:力偶中两力之间的垂直距离h ,称为力偶臂。
力偶的作用面:力偶所在的平面。
2、 力偶矩力偶使物体产生绕某点转动的效应。
F F '-=()()()O O A BA B AB M M F M F F r F r r r F r F''=+=⨯+⨯=-⨯=⨯若任意另取一点仍有AB M r F =⨯。
第二章力系的等效与简化一、刚体和平衡的概念刚体:在受力作用后而不产生变形的物体称为,刚体是对实际物体经过科学的抽象和简化而得到的一种理想模型。
而当变形在所研究的问题中成为主要因素时(如在材料力学中研究变形杆件),一般就不能再把物体看作是刚体了。
平衡:指物体相对于地球保持静止或作匀速直线运动的状态。
显然,平衡是机械运动的特殊形态,因为静止是暂时的、相对的,而运动才是永衡的、绝对的。
二、力系、等效力系、平衡力系力系:作用在物体上的一组力。
按照力系中各力作用线分布的不同形式,力系可分为:(1)汇交力系力系中各力作用线汇交于一点;(2)力偶系力系中各力可以组成若干力偶或力系由若干力偶组成;(3)平行力系力系中各力作用线相互平行;(4)一般力系力系中各力作用线既不完全交于一点,也不完全相互平行。
按照各力作用线是否位于同一平面内,上述力系各自又可以分为平面力系和空间力系两大类,如平面汇交力系、空间一般力系等等。
等效力系:两个力系对物体的作用效应相同,则称这两个力系互为等效力系。
当一个力与一个力系等效时,则称该力为力系的合力;而该力系中的每一个力称为其合力的分力。
把力系中的各个分力代换成合力的过程,称为力系的合成;反过来,把合力代换成若干分力的过程,称为力的分解。
平衡力系:若刚体在某力系作用下保持平衡。
在平衡力系中,各力相互平衡,或者说,诸力对刚体产生的运动效应相互抵消。
可见,平衡力系是对刚体作用效应等于零的力系。
第一节静力学基本公理静力学公理是人们从实践中总结得出的最基本的力学规律,这些规律的正确性已为实践反复证明,是符合客观实际的。
一、二力平衡公理作用于刚体上的两个力平衡的充分与必要条件是这两个力大小相等、方向相反、作用线相同。
这一结论是显而易见的。
如图所示直杆,在杆的两端施加一对大小相等的拉力(F1、F2)或压力(F2、F1),均可使杆平衡。
图2-1应当指出,该条件对于刚体来说是充分而且必要的;而对于变形体,该条件只是必要的而不充分。
如柔索当受到两个等值、反向、共线的压力作用时就不能平衡。
在两个力作用下处于平衡的物体称为二力体;若为杆件,则称为二力杆。
根据二力平衡公理可知,作用在二力体上的两个力,它们必通过两个力作用点的连线(与杆件的形状无关)且等值、反向。
二、加减平衡力系公理在作用于刚体上的已知力系上,加上或减去任意平衡力系,不会改变原力系对刚体的作用效应。
这是因为平衡力系中,诸力对刚体的作用效应相互抵消,力系对刚体的效应等于零。
根据这个原理,可以进行力系的等效变换。
推论1 力的可传性原理作用于刚体上某点的力,可沿其作用线任意移动作用点而不改变该力对刚体的作用效应。
利用加减平衡力系公理,很容易证明力的可传性原理。
设力F作用于刚体上的A点。
现在其作用线上的任意一点B加上一对平衡力系F1、F2,并且使F1= —F2=F,根据加减平衡力系公理可知,这样做不会改变原力F对刚体的作用效应,再根据二力平衡条件可知,F2和F亦为平衡力系,可以撤去。
所以,剩下的力F1与原力F等效。
力F1即可看成为力F沿其作用线由A点移至B点的结果。
同样必须指出,力的可传性原理也只适用于刚体而不适用于变形体。
三、力的平行四边形法则作用于物体同一点的两个力,可以合成为一个合力,合力也作用于该点,其大小和方向由以两个分力为邻边的平行四边形的对角线表示,即合力矢等于这两个分力矢的矢量和。
其矢量表达式为FR= F1 + F2 (1—1)在求两共点力的合力时,为了作图方便,只需画出平行四边形的一半,即三角形便可。
其方法是自任意点O开始,先画出一矢量F1,然后再由F1的终点画另一矢量F2,最后由O点至力矢F2的终点作一矢量FR,它就代表F1、F2的合力矢。
合力的作用点仍为F1、F2的汇交点A。
这种作图法称为力的三角形法则。
显然,若改变F1、F2的顺序,其结果不变。
利用力的平行四边形法则,也可以把作用在物体上的一个力,分解为相交的两个分力,分力与合力作用于同一点。
实际计算中,常把一个力分解为方向已知的两个(平面)或三个(空间)分力,如图1—7即为把一个任意力分解为方向已知且相互垂直的两个(平面)或三个(空间)分力。
这种分解称为正交分解,所得的分力称为正交分力。
四、两个力共面,且作用线通过此交点,构成平面汇交力系。
这是物体上作用的三个不平行力相互平衡的必要条件。
应当指出,三力平衡汇交公理只说明了不平行的三力平衡的必要条件,而不是充分条件。
它常用来确定刚体在不平行三力作用下平衡时,其中某一未知力的作用线。
五、作用力与反作用力公理两个物体间相互作用的一对力,总是大小相等、方向相反、作用线相同,并分别而且同时作用于这两个物体上。
这个公理概括了任何两个物体间相互作用的关系。
有作用力,必定有反作用力;反过来,没有反作用力,也就没有作用力。
两者总是同时存在,又同时消失。
因此,力总是成对地出现在两相互作用的物体上的。
要区别二力平衡公理和作用力与反作用力公理之间的关系,前者是对一个物体而言,而后者则是对物体之间而言。
第一节平面汇交力系合成平面汇交力系的合成方法可以分为几何法与解析法,其中几何法是应用力的平行四边形法则(或力的三角形法则),用几何作图的方法,研究力系中各分力与合力的关系,从而求力系的合力;而解析法则是用列方程的方法,研究力系中各分力与合力的关系,然后求力系的合力。
下面分别介绍。
一、几何法首先回顾用几何法合成两个汇交力。
如图2—1a,设在物体上作用有汇交于O点的两个力F1和F2,根据力的平行四边形法则,可知合力R的大小和方向是以两力F1和F2为邻边的平行四边形的对角线来表示,合力R的作用点就是这两个力的汇交点O。
也可以取平行四边形的一半即利用力的三角形法则求合力如图2—1b所示。
图2—1对于由多个力组成的平面汇交力系,可以连续应用力的三角形法则进行力的合成。
设作用于物体上O点的力F1、F2、F3、F4组成平面汇交力系,现求其合力,如图2—2a所示。
应用力的三角形法则,首先将F1与F2合成得R1,然后把R1与F3合成得R2,最后将R2与F4合成得R,力R就是原汇交力系F1、F2、F3、F4的合力,图2—2b所示即是此汇交力系合成的几何示意,矢量关系的数学表达式为R=F1+F2+F3+F4 (2—1)实际作图时,可以不必画出图中虚线所示的中间合力R1和R2,只要按照一定的比例尺将表达各力矢的有向线段首尾相接,形成一个不封闭的多边形,如图2—2c所示。
然后再画一条从起点指向终点的矢量R,即为原汇交力系的合力,如图2—2d所示。
把由各分力和合力构成的多边形abcde称为力多边形,合力矢是力多边形的封闭边。
按照与各分力同样的比例,封闭边的长度表示合力的大小,合力的方位与封闭边的方位一致,指向则由力多边形的起点至终点,合力的作用线通过汇交点。
这种求合力矢的几何作图法称为力多边形法则。
从图2—2e还可以看出,改变各分力矢相连的先后顺序,只会影响力多边形的形状,但不会影响合成的最后结果。
图2—2将这一作法推广到由n个力组成的平面汇交力系,可得结论:平面汇交力系合成的最终结果是一个合力,合力的大小和方向等于力系中各分力的矢量和,可由力多边形的封闭边确定,合力的作用线通过力系的汇交点。
矢量关系式为:R=F1+F2+F3+……+Fn=∑Fi (2—1b)或简写为R=∑F (矢量和)(2—1c)若力系中各力的作用线位于同一条直线上,在这种特殊情况下,力多边形变成一条直线,合力为R=∑F (代数和)(2—2)需要指出的是,利用几何法对力系进行合成,对于平面汇交力系,并不要求力系中各分力的作用点位于同一点,因为根据力的可传性原理,只要它们的作用线汇交于同一点即可。
另外,几何法只适用于平面汇交力系,而对于空间汇交力系来说,由于作图不方便,用几何法求解是不适宜的。
对于由多个力组成的平面汇交力系,用几何法进行简化的优点是直观、方便、快捷,画出力多边形后,按与画分力同样的比例,用尺子和量角器即可量得合力的大小和方向。
但是,这种方法要求这图精确、准确,否则误差会较大。
二、解析法求解平面汇交力系合成的另一种常用方法是解析法。
这种方法是以力在坐标轴上的投影为基础建立方程的。
1、力在平面直角坐标轴上的投影设力F用矢量AB表示如图2—3所示。
取直角坐标系oxy,使力F在oxy平面内。
过力矢AB的两端点A和B分别向x、y轴作垂线,得垂足a、b及a/、b/,带有正负号的线段ab与a/b/分别称为力F在x、y轴上的投影,记作Fx、Fy。
并规定:当力的始端的投影到终端的投影的方向与投影轴的正向一致时,力的投影取正值;反之,当力的始端的投影到终端的投影的方向与投影轴的正向相反时,力的投影取负值。
力的投影的值与力的大小及方向有关,设力F与x轴的夹角为α,则从图2—3可知ααsin cos F F F F y x -== (2—3)一般情况下,若已知力F 与x 和y 轴所夹的锐角分别为α、β,则该力在x 、y 轴上的投影分别为βαcos cos F F F F y x ±=±= (2—4)即力在坐标轴上的投影,等于力的大小与力和该轴所夹锐角余弦的乘积。
当力与轴垂直时,投影为零;而力与轴平行时,投影大小的绝对值等于该力的大小。
图2—3 图2—4反过来,若已知力F 在坐标轴上的投影Fx 、Fy ,亦可求出该力的大小和方向角:xyy x F F F F F =+=αtan 22 (2—5)式中α为力F 与x 轴所夹的锐角,其所在的象限由Fx 、Fy 的正负号来确定。
在图2—3中,若将力沿x 、y 轴进行分解,可得分力Fx 和Fy 。
应当注意,力的投影和分力是两个不同的概念:力的投影是标量,它只有大小和正负;而力的分力是矢量,有大小和方向。
它们与原力的关系各自遵循自己的规则。
在直角坐标系中,分力的大小和投影的绝对值是相同的。
同时,力的矢量也可以转化为力的标量进行计算,即F=Fx+Fy=jF F y x +i (2—6)式中i 、j 分别为沿直角坐标轴x 、y 轴正向的单位矢量。
力在平面直角坐标轴上的投影计算,在力学计算中应用非常普遍,必须熟练掌握。
例2—1 如图2—4所示,已知NF N F N F N F 400,300,200,1004321====,各力的方向如图,试分别求各力在x 轴和y 轴上的投影。
力力在x 轴上的投影(αcos F ±)力在y 轴上的投影(αsin F ±)F1 N 1000cos 100=⨯ο 00sin 100=⨯ο F2 N 10060cos 200-=⨯-οN 310060sin 200=⨯ο F3 N 15060cos 300-=⨯-ο N 315060sin 300-=⨯-οF4N 220045cos 400=⨯οN 220045sin 400-=⨯-ο为了用解析法求平面汇交力系的合力,必须先讨论合力及其分力在同一坐标轴上投影的关系。