下载文档原格式
16 第2章 力系的简化 2.1 主要内容2.1.1 汇交力系汇交力系合成为通过汇交点的合力，合力的大小、方向等于各分力的矢量和F F R ∑=或 汇交力系的合力在轴上的投影等于各分力在同一轴上的投影的代数和，称之为合力投影定理，即R R R 111,,nnnx xi y yi z zi i i i F F F F F F ======∑∑∑2.1.2 力偶系力偶系合成结果为一合力偶，其力偶矩M 等于各力偶矩的矢量和：∑==ni i1MM合力偶矩矢在各直角坐标轴上的投影：∑∑∑======ni ziz ni yi y ni xi x MM MM MM 111,,或 k j i M iz iy ix M M M ∑+∑+∑=平面力偶系可合成为一合力偶，合力偶矩等于各分力偶矩的代数和：i M M ∑=2.1.3 任意力系力的平移定理作用在刚体上的力，可平行移动到刚体上任一点，平移时需附加一力偶，附加力偶的矩等于原作用力对平移点之矩，称为力的平移定理。
该定理表明，一个力可以等效于一个力和一个力偶。
其逆定理表明，可将平面内的一个力和一个力偶等效于一个力。
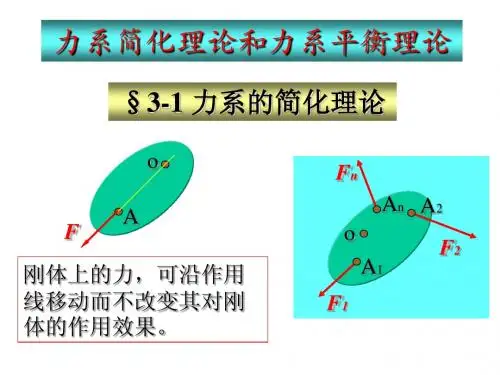
用一简单力系等效地替代一复杂力系称为力系的简化或合成，应用力的平移定理，将力系向一点简化的方法是力系简化的普遍方法。
kj i F z y x F F F ∑+∑+∑=R17力系向一点简化·主矢和主矩力系向任一点O （称简化中心）简化，得到通过简化中心的一个力及一个力偶。
力系中各力的矢量和称为力系的主矢量。
即F F ∑='R主矢与简化中心位置无关力系中各力对简化中心之矩的代数和称为力系对简化中心的主矩。
即)(F O O M M ∑=主矩与简化中心位置有关。
力系的简化结果归结为计算两个基本物理量——主矢和主矩。
它们的解析表达式分别为R1111()nni i i i n nO i O i i i ====⎫''==⎪⎪⎬⎪==⎪⎭∑∑∑∑F F F M M M F 力的大小、方向等于力系的主矢量，力偶矩矢等于力系对O 点的主矩。
