下载文档原格式
3.4实际问题与一元一次方程（探究二）设计者：闫晓刚迟璐一、学习目标1、结合球赛积分表，掌握从表中获取信息的方法，发展观察与推理能力2、通过探索球赛积分与胜负场数之间的数量关系，进一步体会一元一次方程是解决实际问题的数学模型，增强运用数学知识解决问题的意识，激发学习数学的热情3、通过球赛积分问题的探究，认识由实际问题得到的方程的解要符合实际意义，训练思维的严密性重点：从表格中获取有关数据信息，利用方程进行计算、推理、判断难点：从图表中获取有关数据信息，寻找数量之间的隐蔽关系，正确建立方程二、课前预习1、你知道篮球比赛时是如何计算积分的？2、如果不知道积分规则，你能从比赛后的积分表中得出来吗？三、引导自学，探索新知1、某次篮球赛积分榜问题：1）用式子表示总积分与胜、负场数之间的数量关系2）某队的胜场总积分能等于它的负场总积分吗？分析：①观察积分榜，从最下面的一行数据可以发现：负一场积分②设胜一场积分，从表中其他任何一行可以列方程：③用表中其他行可以验证，得出此次比赛的积分规则：负一场积分，胜一场积分④如何计算总积分？总积分= + =如果一个队胜m场，则负场，胜场积分为分，负场积分为分总积分为⑤某队的胜场总积分能等于它的负场总积分吗？设某个队胜了x场，则负了场如果这个队的胜场积分等于负场积分，则得方程：解这个方程，得由于这里x的值必须是整数，所以2、触类旁通1）某班的一次数学小测验中，共出了20道选择题，每题5分，总分100分，现从中抽出5份试卷进行分析，如下表：有一同学说：同学甲得了70分，同学乙得了85分，谁的成绩是准确的？为什么？2）一足球邀请赛，勇士队在第一轮比赛中共赛了9场，得分17分。
比赛规定胜一场得3分，平一场得1分，负一场得0分。
勇士队在这一轮中只负了2场，那么这个队胜了几场？又平了几场？3）观察下面的日历，一个竖列上的相邻的3个数之间有什么关系？①如果设其中的一个数为x ，那么其它两个数怎么表示？②如果这三个数的和是a ，根据你设的未知数x ，列出方程， 求出这3天分别是几号吗？③如果小颖说出的和是60，你能求出这3天分别是几号吗？为什么？④如果小颖说出的和是21，你能求出这3天分别是几号吗？为什么？四、小结通过本节课的学习你有哪些收获？你还有哪些疑惑？ 五、作业 导航6059P ~P。
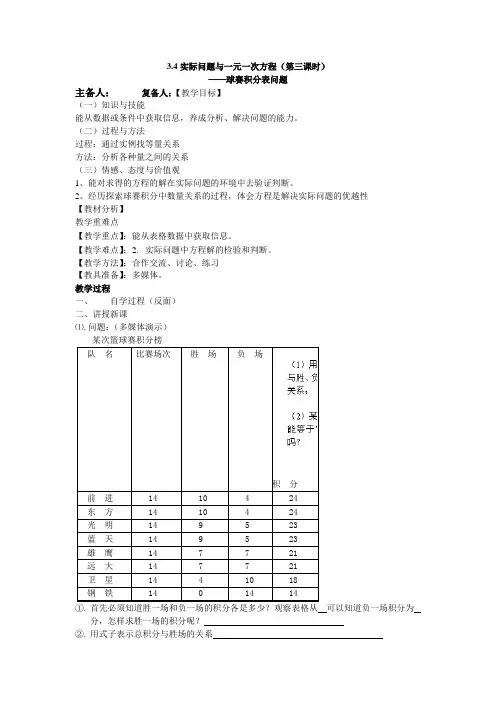
3.4实际问题与一元一次方程（第三课时）——球赛积分表问题主备人：复备人：【教学目标】（一）知识与技能能从数据或条件中获取信息，养成分析、解决问题的能力。
（二）过程与方法过程：通过实例找等量关系方法：分析各种量之间的关系（三）情感、态度与价值观1、能对求得的方程的解在实际问题的环境中去验证判断。
2、经历探索球赛积分中数量关系的过程，体会方程是解决实际问题的优越性【教材分析】教学重难点【教学重点】：能从表格数据中获取信息。
【教学难点】：2. 实际问题中方程解的检验和判断。
【教学方法】：合作交流、讨论、练习【教具准备】：多媒体。
教学过程一、自学过程（反面）二、讲授新课⑴.问题：（多媒体演示）某次篮球赛积分榜积分①. 首先必须知道胜一场和负一场的积分各是多少？观察表格从可以知道负一场积分为分，怎样求胜一场的积分呢？②. 用式子表示总积分与胜场的关系用式子表示总积分与负场的关系（提示：胜场或负场的场数并不确定，可以用未知数来表示）③. 完成（2）的解答，完成后谈谈您的感想。
⑵.如果去掉钢铁队的信息，你还能解决这个问题吗？试试看。
解决问题：①.必须知道胜一场和负一场的积分，引导学生观察表格，找到答案。
②.对于（1）中的问题，应引导学生设出一个未知数，用未知数表示这个数量关系。
③.问题（2）学生很容易想到用方程解决，教学中应注意学生对求得的解是否有异议，能否加以验证，指出数据的不合理性。
⑵.延伸：1.在本例中，如果去掉钢铁队那一行的信息，本题能否做出解答。
2.若蓝天队的信息丢失，你能够找回来吗？延伸的问题涉及到多个未知量的表示方法——用等量关系去表达，表格中有很多等量关系，引导学生应用这些等量关系来表示。
三、小试牛刀：1.足球比赛的记分规则为：胜一场得3分，负一场得0分，平一场得l分．一个队打了8 场球，只输了一场，共得17分，那么这个足球队胜了( )A．3场B．4场C．5场D．6场2.为了加强公民的节水意识，合理利用水资源，某市采用价格调控手段达到节水的目的．该市自来水收费价格见价目表．若某户居民月份用水，则应收水费：元．(1）若该户居民月份用水，则应收水费______元；(2）若该户居民、月份共用水(月份用水量超过月份），共交水费元，则该户居民，月份各用水多少立方米四、板书设计3.4实际问题与一元一次方程——球赛积分表问题1.球赛积分表①.获取信息②.字母表示数③.寻找等量关系2.检验方程的解的合理性五、教学后记：本课以学生比较感兴趣的足球为话题引人，然后把生活中的实际问题以表格的形式呈现给学生，提供给学生一个探索问题，掌握利用表格的信息解决问题的空间．然后通过教师的点拨，引导学生读懂表格的信息，求得胜负一场的积分，再通过师生共同合作参与，由学生自主探索得出用式子表示积分与胜负场数之间的数量关系，并探索某队的胜场总积分是否等于它的负场总积分．在整个新授过程中，充分发挥了学生的主体作用．新知识通过学生自主探索，在合作交流过程中得到．教师在过程中扮演了的参与者、合作者、引导、启迪者的角色．这充分体现了新课标的教学理念．。
3.4 实际问题与一元一次方程第3课时球赛积分表问题教学目标:1.会分析表格中的数据,从数据中找出隐含的条件.2.认识数学与生活的紧密联系、数学题目的形式多样性,培养学生学习数学的兴趣.教学重难点:分析表格数据,找出隐含条件,从而求出题目中的问题.教学过程:一、问题呈现课本P103探究2:1.学生分组讨论以下问题.(1)表格涉及的量中,要表示总积分,还需知道什么量?(2)表格中列出8个球队的积分中,只有一个球队的积分与其他球队的积分组成不同,这是哪一个球队?为什么?(3)如何求胜一场、负一场的积分?(4)用式子表示总积分与胜、负场数之间的数量关系?(6)根据以上表格数据解决以下问题:某队的胜场总积分能等于负场总积分吗?某队总积分是19分,该队胜几场?某队的胜场总积分能等于负场总积分的3倍吗?2.小结探究2的解题注意事项:(1)比赛总场次都是14,设胜场为x,则负场为(14-x),根据表格数据求出胜一场、负一场的分数,从而可表示出每个球队的总积分.(2)根据题目问题求出未知数的值后,还要看该未知数的值是否符合实际意义,如比赛场数不能是分数.3.反思:探究2中,用钢铁队的积分情况求出负一场得1分,再用其余任何一个队的积分求出胜一场积分,除了这种方法求负一场、胜一场积分外,如果没有钢铁队的积分,由其它球队的积分如何求胜一场、负一场的积分呢?按这种方法,胜一场、负一场的分都是未知量,可设胜一场得a分,拿前进队来说,如何用含a的式子表示负一场得的分?又以什么为相等关系列出关于a的方程求出a的值?学生分组讨论以上问题.二、巩固练习(1)从两个班可以知道平一场比负一场多得分.(2)若胜一场3分,求平一场、负一场各得几分?(3)某班胜场是平场的2倍,积16分,求这个班胜几场.(4)某班平场是负场的2倍,积15分,可能吗?2.分组合作学习:课本P106练习第3题,提出问题:(1)比较七、八年级文艺小组、科技小组的活动次数和两个年级课外小组活动总时间,可以总结出什么结论?(2)九年级课外小组活动时间7 h等于什么时间与什么时间的和?(3)设未知数解答.三、课时小结根据表格信息解决实际问题的方法.四、阅读课本课本P103~P104关于探究2的内容.2019-2020学年七年级数学上学期期末模拟试卷一、选择题1．下列关于角的说法正确的是（）A.两条射线组成的图形叫做角B.角的大小与这个角的两边的长短无关C.延长一个角的两边D.角的两边是射线，所以角不可度量2．如图，点A位于点O的方向上.( )A．南偏东35°B．北偏西65°C．南偏东65°D．南偏西65°3．已知线段，在直线AB上取一点C，使，则线段AC的长（）A.2B.4C.8D.8或44．若x=-2是关于x的方程2x+m=3的解，则关于x的方程3（1-2x）=m-1的解为（）A. B. C. D.15．如果代数式4y2－2y＋5的值是7，那么代数式2y2－y＋1的值等于( )A．2 B．3 C．－2 D．46．在1，－2，0，53这四个数中，绝对值最大的数是（）A.－2B.0C.53D.17．多项式2x3-8x2+x-1与多项式3x3+2mx2-5x+3的和不含二次项，则m为（）A．2 B．-2 C．4 D．-48．下列计算正确的是（）A．a5+a2＝a7B．2a2﹣a2＝2 C．a3•a2＝a6D．（a2）3＝a6 9．运用等式性质的变形，正确的是（）A.如果 a=b，那么 a+c=b﹣cB.如果a bc c=，那么 a=bC.如果 a=b，那么a bc c= D.如果 a=3，那么 a2=3a210．如图，数轴上有M、N、P、Q四个点，其中点P所表示的数为a，则数-3a所对应的点可能是( )A.MB.NC.PD.Q11．若m是有理数，则m m+的值是（）A.正数B.负数C.0或正数D.0或负数12．下列说法正确的是（）A．一个数的绝对值一定比0大 B．一个数的相反数一定比它本身小C．绝对值等于它本身的数一定是正数 D．最小的正整数是1二、填空题13．如图是一个正方体的展开图，它的六个面上分别写有“构建和谐社会”六个字，将其围成正方体后，与“社”在相对面上的字是_____．14．如图，是的平分线，是内的一条射线，已知比大，则的度数为__________．15．如图所示的运算程序中，若开始输入的x 值为64，我们发现第一次输出的结果为32，第二次输出的结果为16，……，则第2019次输出的结果为_____．16．某中学初三（6）班十几名同学毕业前和数学老师合影留念，一张彩色底片要0.6元，扩印一张相片0.5元，每人分一张，免费赠送老师一张（由学生出钱），每个学生交0.6元刚好，则相片上共有______人．17．有理数a 、b 、c 在数轴上的位置如图，则a c c b a b ++--+=______．18．将2341x x +-减去21x x -+，结果是___________． 19．用“＞”“＜”或“＝”填空．(1)－56________－67； (2)－45________－35；(3)|－7|________0； (4)|－2.75|________|＋234| 20．A ．B ．C 三点相对于海平面分别是－13米、－7米、－20米，那么最高的地方比最低的地方高____米. 三、解答题21．已知，如图，点C 在线段AB 上，且AC=6cm ，BC=14cm ，点M 、N 分别是AC 、BC 的中点．（1）求线段MN的长度；（2）在（1）中，如果AC=acm，BC=bcm，其它条件不变，你能猜测出MN的长度吗？请说出你发现的结论，并说明理由．22．如图，直线AB、CD相交于点O，OE平分∠BOD.(1)若∠AOC=70°,∠DOF=90°，求∠EOF的度数；(2)若OF平分∠COE,∠BOF=15°，求∠AOC的度数。
人教版数学七年级上册3.4《实际问题与一元一次方程球赛积分表问题》教学设计一. 教材分析人教版数学七年级上册3.4《实际问题与一元一次方程球赛积分表问题》这一节主要通过球赛积分表问题引入一元一次方程的实际应用。
学生通过解决这个问题，可以加深对一元一次方程的理解，并能运用到实际问题中。
教材通过这个例子，让学生感受到数学与生活的紧密联系，激发他们对数学的兴趣。
二. 学情分析学生在学习这一节之前，已经学习了一元一次方程的理论知识，对于如何解一元一次方程已经有了一定的了解。
但实际应用一元一次方程解决生活中的问题可能还存在一定的困难。
因此，在教学过程中，教师需要引导学生将理论知识与实际问题相结合，提高他们解决实际问题的能力。
三. 教学目标1.理解球赛积分表问题的背景，掌握解决这类问题的方法。
2.能够运用一元一次方程解决实际问题，提高解决问题的能力。
3.感受数学与生活的紧密联系，激发学习数学的兴趣。
四. 教学重难点1.重点：理解球赛积分表问题的背景，掌握解决这类问题的方法。
2.难点：如何引导学生将一元一次方程理论知识与实际问题相结合。
五. 教学方法采用问题驱动法，通过设置球赛积分表问题，引导学生自主探究，合作交流，从而解决问题。
同时，运用讲解法、示范法等，帮助学生理解问题，掌握解决方法。
六. 教学准备1.准备球赛积分表问题相关的案例。
2.准备教学PPT，包括问题呈现、解题过程、总结等内容。
3.准备黑板，用于板书解题过程和关键知识点。
七. 教学过程1.导入（5分钟）通过一个球赛积分表的案例，引导学生思考如何计算球队的积分。
让学生感受到数学与生活的联系，激发学习兴趣。
2.呈现（10分钟）呈现球赛积分表问题，引导学生观察问题，分析问题。
让学生尝试用自己的方法解决这个问题。
3.操练（10分钟）学生在课堂上独立解决这个问题，教师巡回指导，解答学生的疑问。
在这个过程中，教师可以引导学生运用一元一次方程的知识点。
4.巩固（5分钟）教师挑选几个学生的解题过程，进行讲解和分析，让学生加深对一元一次方程解决实际问题的理解。
3.4实际问题与一元一次方程教学设计（探究2 球赛积分表问题）江西省赣州市南康三中吴志平教学内容多媒体辅助教学、导学案．教学方法情境激趣、观察讨论、讲练结合．教学过程一、创设情境1．生命在于运动．在体育运动中也有很多问题可以用方程来解决，今天我们一起来探讨“球赛积分表问题”．先观看一段小视频．（CBA近期比赛视频）2．引出课题（在比赛即将结束的时候停住画面），比赛即将结束，北京首钢队在暂时落后2分的情况下在三分线外投出最后一球，最终比赛结果如何？先请同学们猜一下：你们认为有哪几种结果呢？（学生回答可能平局时）老师解释：正规的篮球比赛最终结果是不允许出现平局，如果常规时间结束比分相同就要通过加时赛分出胜负．二、问题探究例（课本P103探究2）：观察积分榜，完成下面的问题．（1）用式子表示总积分与胜、负场数之间的数量关系；（2）某队的胜场总积分能等于它的负场总积分吗？老师提问：从这张表格中你能获得哪些信息？学生可能有以下回答：（1）每队比赛总场次是14场．（2）胜场数越多，总积分越多．（师：为什么？）（3）负一场得1分，（师：从哪里看出来的？追问引出下面的答案）（4）胜一场得2分．（师：你是怎么算出来的？）结合学生的回答引导学生说出数量关系：胜场数+负场数＝总场数；胜场积分+负场积分＝总积分如果学生没有用方程的方法，老师提示可不可以用方程思想来解决这个问题呢（即列方程求解）？学生回答完后，展示：设胜一场积x分，从第一行可列方程：10x+ 1 ×4 = 24（问：这样列方程的依据是什么？出示：胜场积分+负场积分＝总积分）解得x= 2．所以胜一场积2分．用其他行的数据验证，得出结论：本次篮球联赛的积分规则是：胜一场积2分，负一场积1分．利用这个积分规则解决问题1、问题2．问题1：请你用式子表示总积分与胜、负场数之间的数量关系．如果设某队胜了m场，则这个队负了(14-m) 场，胜场积分为2m 分，负场积分为(14-m) 分，总积分为2m+(14-m)= (m+14) 分．提示：也可以设某队负了m场．问题2：某队赛14场，它的胜场总积分能等于它的负场总积分吗？这是个判断题，要正确作出判断，需要作出定量分析．学生讨论，如有困难教师点拨：不妨先假设某队的胜场积分等于负场积分．学生独立解答，请一学生演板．订正时屏幕展示完整的解答过程．设一个队胜了x场，则负了（14x-）场，如果胜、负场积分会相等列出方程：214x x=-，解得143x=．分析：因为x表示所胜的场数，所以必须是整数．而这里x的值不是整数，所以不符合实际意义，由此可以判定没有哪个队的胜场积分会等于负场积分．引导学生说说这类问题的解法．老师点评，这类的题目先按能去解答，再看解是否符合实际意义，如果符合，就说明能，如果不符合，就说明不能．归纳：这个问题说明了：1．利用方程不仅能求出具体的数值,而且还可以进行推理判断．2．用方程解决实际问题时，不仅要注意解方程的过程是否正确，而且还要检验方程的解是否符合问题的实际意义．三、课堂练习前面我了解了篮球的积分规则，但其他球赛的积分规则可能不一样，我们通过下面的练习来探索足球比赛的积分规则．1．在2014年巴西世界杯小组赛中，梅西率领的阿根廷队以三战全胜的战绩获得F组第一名，顺利闯入16强．F组积分榜（1）根据表格数据求积分规则：胜一场积______分；平一场积______分；负一场积______分；（2）已知尼日利亚队负1场，那么该队的积分能是5分吗？2．完成课本P106练习第3题．提示学生先求出文艺小组和科技小组的每次活动时间．设九年级文艺小组活动次数为x，科技小组活动次数为y，则可列方程______________然后引导学生用枚举法，找到合理的答案．3．现场抢答题．出示限时答题软件，请两至三位同学到电脑前轮流答题．（答对每题得10分，答错或未答每题扣5分）四、课堂小结通过对球赛积分表的探究，你有什么收获呢?五、课外作业1．阅读作业：课本第104～105页2．必做作业：课本第112页第9题3．选做作业：合作交流共同探讨如果“某次篮球联赛积分榜”中只有前进队和卫星队两行数据（如下图），你还能求出胜一场和负一场的积分各是多少吗？六、揭晓球赛结果七、板书设计八、教学反思。
