最新《球赛积分表问题》案例
- 格式:doc
- 大小:73.00 KB
- 文档页数:7

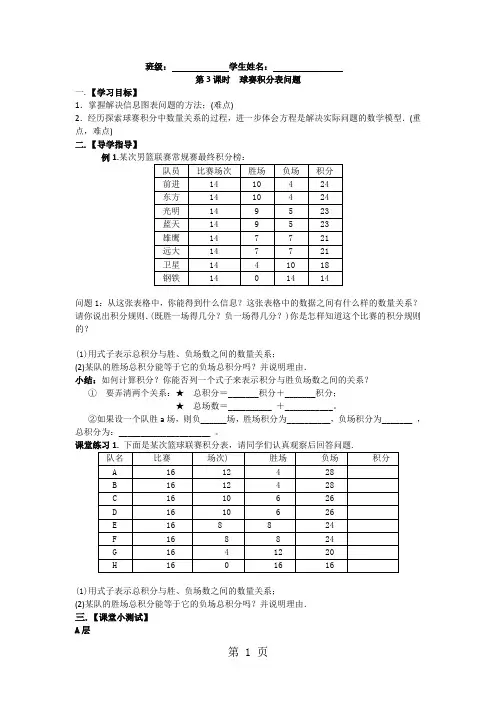
班级:学生姓名:第3课时球赛积分表问题一.【学习目标】1.掌握解决信息图表问题的方法;(难点)2.经历探索球赛积分中数量关系的过程,进一步体会方程是解决实际问题的数学模型.(重点,难点)二.【导学指导】例1.问题1:从这张表格中,你能得到什么信息?这张表格中的数据之间有什么样的数量关系?请你说出积分规则.(既胜一场得几分?负一场得几分?)你是怎样知道这个比赛的积分规则的?(1)用式子表示总积分与胜、负场数之间的数量关系;(2)某队的胜场总积分能等于它的负场总积分吗?并说明理由.小结:如何计算积分?你能否列一个式子来表示积分与胜负场数之间的关系?①要弄清两个关系:★总积分=_______积分+_______积分;★总场数=__________ +___________。
②如果设一个队胜a场,则负______场,胜场积分为__________,负场积分为_______ ,总积分为:_____________________ 。
(1)用式子表示总积分与胜、负场数之间的数量关系;(2)某队的胜场总积分能等于它的负场总积分吗?并说明理由.三.【课堂小测试】A层1.某次知识竞赛共20道题,每答对一题得8分,答错或不答要扣3分.某选手在这次竞赛中共得116分,那么他答对几道题?2.某班的一次数学小测验中,一共出了20道选择题,每题5分,总分为100分,现从中抽取5份试卷,进行分析,如下表:(1)某同学得了70分,问他答对了多少道题?(2)同学甲说他自己得了86分,同学乙说他自己得了72分,请你判断一下:谁说的是真话?为什么?B层1.有一批货物需要从A地运往B地,货主准备租用甲、乙两种货车,已知过去两次租用这两种货车运货情况如下表.现租用3辆甲种货车和5辆乙种货车,一次刚好运完这批货物,如果按每吨付502.例如:一户居民七月份用电420度,则需缴电费420×0.85=357(元).某户居民五、六月份共用电500度,缴电费290.5元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度.问该户居民五、六月份各用电多少度?。

球赛积分表问题解决有关表格的问题时,首先要根据表格中给出的相关信息,找出数量间的关系,然后再运用数学知识解决问题.例1 某次知识竞赛共20道题,每答对一题得8分,答错或不答要扣3分. 某选手在这次竞赛中共得116 分,那么他答对几道题?例2.甲、乙、丙、丁四支球队有资格参加亚洲冠军联赛八组足球比赛(主客场),结束后积分表如下:球队胜场平场负场总进球数总失球数积分甲42014314乙41112613丙2136107丁006x150(1)填空:表格中x的值是.(2)比赛规定:胜一场积分,平一场积分.(3)若甲队在争取资格的预赛中进行了12场比赛,其中负5场,积分共得19分,那么这支球队胜了多少场才能进人决赛?(4)在这次亚洲冠军杯的其他小组比赛中,能否出现一支球队保持不败的战绩(6场比赛都不输),且胜场总积分恰好等于它的平场总积分?练习1.某球队参加比赛,开局9 场保持不败,积21 分,比赛规则:胜一场得3 分,平一场得1分,则该队共胜场.2.足球比赛中,若胜一场记3分,平一场记1分,负一场记﹣2分.甲队获得9分,该队可能()A.胜3场,平3场,负3场B.胜3场,平1场,负1场C.胜3场,平2场,负1场D.胜3场,平2场,负2场3.中国男篮CBA职业联赛的积分办法是:胜一场积2 分,负一场积1 分,某支球队参加了12 场比赛,总积分恰是所胜场数的4 倍,则该球队共胜____场.4.足球比赛积分规则为:胜一场记3分,平一场得1分,负一场得0分,一个队进行了13场比赛,其中负了4场共得19分,那么这个队胜了场.5.足球比赛的记分规则是:胜一场记3分,平一场记1分,负一场记0分.一支中学生足球队参加了15场比赛,负了4场,共得29分,则这支球队胜了6.足球比赛的计分规则是:胜一场得3分,平一场得1分,负一场得0分.一队打16场,负7场,共得19分,那么这个队共胜了7.某班级乒乓球比赛的积分规则:胜一场得2分,负一场得-1分.一个选手进行了20场比赛,共得28分,则这名选手胜了多少场(说明:比赛均要分出胜负)?8.初一级进行法律知识竞赛,共有30题,答对一题得4分,不答或答错一题倒扣2分。



球赛积分表问题案例彭谷芳教学内容:球赛积分表问题教学目标:1:学会解决信息图表问题的方法2:经历探索球赛积分中数量关系的过程,进一步体会方程是解决的数学问题的模型,明确用方程解决实际问题时,还要检验方程的解是否符合问题实际意义。
3:在探索中体会学习的乐趣。
教学重点:解决信息图表问题教学难点:从图表中获取有用的信息教学媒体:多媒体教学课时:1课时一:情景引入观看视频:中国男篮获得伦敦奥运会门票,设计意图:由中国男篮获得伦敦奥运会门票激起学生的爱国情感同时引入本节课的课题--------球赛积分表问题,为提出下面的问题作铺垫。
二:提出问题某次篮球联赛积分榜(1)用式表示总积分与胜. 负场数之间的数量关系;(2)某队的胜场总积分能等于它的负场总积分吗?设计意图:解决这个图表问题是本节课的重点,让学生明确本节课的重点是什么。
三:解决问题师:从这张表格的横向和纵向你分别能得到什么信息?(学生分组讨论,由一个学生统计讨论结果)生1:我从表格的纵向看出,本次比赛共有八个队参加,分别是:前进,东方,光明,蓝天,雄鹰,远大,卫星,钢铁。
每个队都打14场比赛。
师:说得很棒。
除了这些信息之外,从纵向还能看出什么信息?生2:我从纵向还可以看出每个队的胜的场数和负的场数,如:前进队胜了10场负了4场,东方队胜了10场负了4场-------而且每个队在本次比赛中的总积分也能读出来。
如:雄鹰队本次比赛总积分为21分,钢铁队总积分为14分。
师:眼光很独到。
原来从表格的纵向可以读出这么多的信息,那从表格的横向又可以得到哪些信息,大家可以畅所欲言。
生3:每个队的:胜的场数+负的场数=14场胜场的积分+负场的积分=总积分师:太精彩了!你们能分别找出卫星,钢铁的胜场数、负场数和总积分吗?生4:卫星胜了4场,负了10场总积分为18分,钢铁胜了0场负了14场总结积分为14分。
师: 很准确。
在这八个队中有没有很特殊的,能够看出胜一场积几分,负一场积几分?生5:钢铁队胜0场,负14场,总积分为14分,可以看出每负一场积1分。




《球赛积分表问题》教学案例
保康县过渡湾镇中心学校:周香波
设计意图:
在近几年的数学中考试题中 ,试题背景越来越趋向社会化 ,把一些社会热点问题抽象成数学问题 ,不但体现了时代特征 ,也考查了学生对数学知识的掌握程度和运用数学知识解决实际生活问题的能力 ,这符合新的课程标准的精神 .我对 2014年各地中考试卷中有关的实际问题采撷。
从生活中的问题引导学生思考探究获得经验。
感受数学来源于生活并应用于生活,揭示生活中的现象。
体现提出问题,解决问题到获取方法及经验这样的思路。
学情分析:
学生学习的心理基础和认知特点来说,学生在前一阶段的学习过程中已经具备了实际问题建立一元一次方程和解一元一次方程的一般步骤的基础,能进行数学建模和简单的解释应用。
对于七年级的学生来说他们虽具有一定的分析、理解、筛选信息的能力。
教材分析:
《数学课程标准》对本章知识的要求是:“能够根据具体情况中的数量关系列出方程,体会方程是刻画现实世界数量关系的有效模型。
”从本章知识的安排上来看,对实际问题的讨论是贯穿全章的一条主线,本章中对一元一次方程解法的讨论始终是围绕实际问题进行的,及先列方程,讨论如何解方程,这是本章教材编写的一个特点。
而本节内容是有理数、整式加减之后的内容。
在前面两节已经讨论过由实际问题建立
一元一次方程和解一元一次方程的一般步骤的基础上,进一步以“探究”的形式讨论如何用一元一次方程解决实际问题。
本节课是一节《实际问题与一元一次方程》的第二课,选择球赛积分表的问题作为探究点,不仅仅是为了探究如何解决这个具体问题,而是想让学生通过这个问题的解决,进一步体验“建模解题”的过程,渗透建模思想。
另一方面使学生能在更加贴近实际生活的问题情境中运用所学数学知识,激发学生学习数学的兴趣,使学生在分析问题和解决问题的能力、创新精神和实践意识在更高层次上得到提高。
教学目标:
知识技能:掌握应用方程解决实际问题的方法步骤,提高分析问题、解决问题的能力。
情感态度:鼓励学生自主探究,合作交流,养成自觉反思的良好习惯。
重点:把实际问题转化为数学问题,不仅会列方程求出问题的解,还会进行推理判断。
难点:把数学问题转化为数学问题。
关键:从积分表中找出等量关系。
教法:探究、讨论、启发式教学。
教学过程:
一、创设问题情境
课件展示几张NBA,CBA比赛场面及比分图片。
(学习是生活需要,引起学生兴趣)
二、合作互学
教师用课件展示课本103页中“篮球联赛积分榜”引导学生观察,思考:①用式子表示总积分能与胜、负场数之间的数量关系;
②某队的胜场总分能等于它的负场总积分么?
三、精讲导学
先让学生充分思考、合作交流,然后教师引导学生一起合作完成问题分析。
师:要解决问题①必须求出胜一场积几分,负一场积几分,你能从积分榜中得到负一场积几分么?你选择哪一行最能说明负一场积几分?
生:从最下面一行可以发现,负一场积1分。
师:胜一场呢?
生:2分(有的用算术法、有的用方程各抒己见)
师:若一个队胜a场,负多少场,又怎样积分?
生:负(14-a)场,胜场积分2a,负场积分14-a,总积分a+14.
师:问题②如何解决?
学生通过计算各队胜、负总分得出结论:不等。
师:你能用方程说明上述结论么?
生:老师,没有等量关系。
师:欸,就是,已知里没说,是不是不能用方程解决了?谁又没有大胆设想?
生:老师,能不能试着让它们相等?
师:伟大的发明都是在尝试中进行的,试试?
生:如果设一个队胜了x场,则负(14-x)场,让胜场总积分等负场总积分,方程为:2x=14-x解得x=14/3
师:x表示什么?可以是分数么?由此你的出什么结论?
生:x表示胜得场数,应该是一个整数,所以,x=4/3不符合实际意义,因此没有哪个队的胜场总积分等于负场总积分。
师:此问题说明,利用方程不仅求出具体数值,而且还可以推理判断,是否存在某种数量关系;还说明用方程解决实际问题时,不仅要注意方程解得是否正确,还要检验方程的解是否符合问题的实际意义。
拓展延伸:
如果删去积分榜的最后一行,你还能用式子表示总积分与胜、负场数之间的数量关系吗?
先让学生独立思考、后交流。
遇有困难教师引导。
师:我们可以从积分榜中积分不相同的两行数据求的胜负一场各得几分,如:一、三行。
教师引导学生设未知数,列方程。
学生试说。
生:设胜一场积x分,则前进队胜场积分10x,负场积分(24-10x)分,它负了4场,所以负一场积分为(24-10x)/4,同理从第三行得到负一场积分为(23-9x)/5,从而列方程为(24-10x)/4=(23-9x)/5。
解得x=2,当x=2时,(24-10x)/4=1。
仍然可得负一场积1分,胜一场积2分。
四、展示竟学
已知某山区的平均气温与该山的海拔高度的关系见表:
若某种植物适宜生长在18℃——20℃(包括18℃——20℃)的山区,请问该植物适宜种在海拔为多少米的山区?
学生分析题意,思考,在练习本上完成,然后同桌小议,代表发言,教师点拨。
五、小结评学:1、让几个学生谈自己的学习体验,再请一两个学生交流。
(略)
2
六、布置作业:课本107页8、9题。
教学反思
本节课主要是借球赛积分表问题传授数学知识的应用。
在前面已经讨论过由实际问题抽象出一元一次方程模型和解一元一次方程的基础上,本节进一步以“探究”的形式讨论如何用一元一次方程解决实际问题。
要探究的问题比前几节的问题复杂些,问题情境与实际情况更接近。
本节的重点是建立实际问题的方程模型。
通过探究活动,进一步体验一元一次方程与实际的密切联系,加强数学建模思想,培养运用一元一次方程分析和解决问题的能力。
由于本节问题的背景和表达都比较贴近实际,其中的有些数量关系比较隐蔽,所以在探究过程中正确建立方程是难点,教师要恰当的引导,让学生弄清问题背景,分析清楚有关数量关系,找出可作为方程依据的
主要相等关系,但教师不要代替学生的思考。
2015年湖北省宜昌市中考数学试卷
一、选择题(下列各题中,只有一个选项是符合题目要求的,本大题共15小题,每小题3分,计45分)
1.(3分)(2015•宜昌)中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为()A.44×108B.4.4×109C.4.4×108D.4.4×1010
2.(3分)(2015•宜昌)下列剪纸图案中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.
3.(3分)(2015•宜昌)陆地上最高处是珠穆朗玛峰顶,高出海平面8848m,记为+8848m;陆地
上最低处是地处亚洲西部的死海,低于海平面约415m,记为()
A.+415m B.﹣415m C.±415m D.﹣8848m
4.(3分)(2015•宜昌)某校对九年级6个班学生平均一周的课外阅读时间进行了统计,分别为(单位:h ):3.5,4,3.5,5,5,3.5.这组数据的众数是()
A.3B.3.5 C.4D.5
5.(3分)(2015•宜昌)如图是一个可以自由转动的转盘,转盘分为6个大小相同的扇形,指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),指针指向阴影区域的概率是()
A.B.C.D.
6.(3分)(2015•宜昌)下列式子没有意义的是()
A.B.C.D.
7.(3分)(2015•宜昌)不等式组的解集在数轴上表示正确的是()A.B.C.D.。