当前位置：文档之家 › 电路分析基础第五版第7章

电路分析基础第五版第7章

  • 格式：ppt
  • 大小：4.48 MB
  • 文档页数：98

下载文档原格式

  / 98

合集下载

南京邮电大学电路分析基础_第7章2

南京邮电大学电路分析基础_第7章2

率因数pf=0.5，欲并联电容使负载的功
率因数提高到0.8(滞后),求电容。
解：负载电流有效值:
P
1.1103
I
10A
U pf 220 0.5
I' I
U C
IC
感性 负载
感性负载的阻抗角: Z arccos 0.5 60 设电压相量为： U 2200 V
则负载电流相量: I 10 60 A
并联电容后，电源电流有效值:
I ' P 1.1103 6.25A U pf ' 220 0.8
由于pf’=0.8 (滞后), 因此功率因数角:
Z ' arccos 0.8 36.9
I' 6.25 36.9 A
I'
U
IC I
IC I'I 6.25 36.9 10 60 5 j3.75 - (5 - j8.66) 4.9190 A
所获最大功率：
Pmax
U
2 oc
4 Ro
最大功率传输定理：工作于正弦稳态的
网 络 向 一 个 负 载 ZL=RL+jXL 供 电 ， 由 戴
维南定理(其中 Zo=Ro+jXo)，则在负载阻
抗等于含源网络输出阻抗的共轭复数(即
）时ZL，
*
Zo
负载可以获得最大平均功率：
Pmax
U
2 oc
4 Ro
满足 ZL 的Z* o匹配，称为共轭匹配。
5、无功功率
p(t) U I cosZ U I cos(2 t Z ) U I cosZ U I cosZ cos 2t U I sin Z sin 2 t U I cosZ (1 cos 2 t) U I sin Z sin 2 t

电路分析基础习题第七章答案

电路分析基础习题第七章答案
•
i2 (t) 2 co 4s t 0 (5 0 )0 A, I2 250A
电压滞后电流900，该二端元件为电容元件
•
(3) u 3 (t) 1c 0o 2s0 t (6 0 )0 V，U3 5 260V
i3(t)5si2 n0 (t 0 15 )A0 ， I•3
52 2
60A
电压与电流同相位，该二端元件为电阻元件
OC
S
S
等效阻抗： Z j2 eq
•
•
U
I OC 5.774 j6.667 8.819 130.89
Z j5 eq
8.如图所示电路，求其戴维南等效相量模型。
解：求开路电压，根据如图的相量模型：
•
I
3 0 6
3 0 6 4 4 ( 1 j) 2 ( 1 j)
9 j6 j6 /j6 / 9 j6 j 31 j 2
8.819 130.89
j5
（3）叠加定理，等效电路图为图
电流源单独作用时， I•1j2j 2j51 030 2 3 030A
电压源单独作用时，
•
I2
100j10A，
j3
3
• ••
总电流 II1I2 5 .77 j4 6 .67 A （4）戴维南定理，等效电路图为图
开路电压：
•
•
•
U I j2 U 1030 j2 100 20 j17.32
1 jC
• I
•
•
B.U (R C) I
D.
•
U
R
1 jC
•
I
•
R
I
+•
U
C
-
图 选择题 5 图

邱关源五版电路 第七章-文档资料

邱关源五版电路 第七章-文档资料
10
0
u ( t ) 10 e kV t 0 V
2500 t
uV (0+)= - 10000V
造成 V 损坏。 -10kV
4
例3: Photoflash Unit
2k R1 1 S 80V US 2 + 4 R2 C uC photolamp 2mF
BUCT
i
?
US
U R
在冲激函数激励下一阶电路的零状态响应。 注意：激励是冲激函数，响应不一定是冲激函数。 方法1： 积分法 （1）关键是求得冲激过后瞬间，在储能元件上所获得 的状态变量的初始值uC(0+)或 iL(0+)； （2）然后求零输入响应的过程：
BUCT
步骤： A、用戴氏（或诺顿）定理将电路简化；
B、对电路列写KVL或KCL方程→积分→求得状态 变量的初始值uC(0+)或 iL(0+) ； C、用三要素法写出t≥0后的电路响应 零输入响应） f (t)= f (0+) e-t/ (t) 。
(t )
9
2.延迟的单位阶跃函数 (t-t0)
BUCT
1
0
t0
t
0 (t t0) (t t0) 1 (t t0)
3.用单位阶跃信号可方便地表示各种信号
例1
1 0
f(t) 1
f(t)
(t) t - (t-t0)
f ( t ) ( t ) ( t t ) 0

解：方法1：
u s( t )
Us 0
用阶跃函数表示激励，求阶跃响应。
us (t) =Us (t) –Us (t–)
RC电路电容端电压uC的单位阶跃响应为： t t ) s ( t ) ( 1 e ( t ) u C

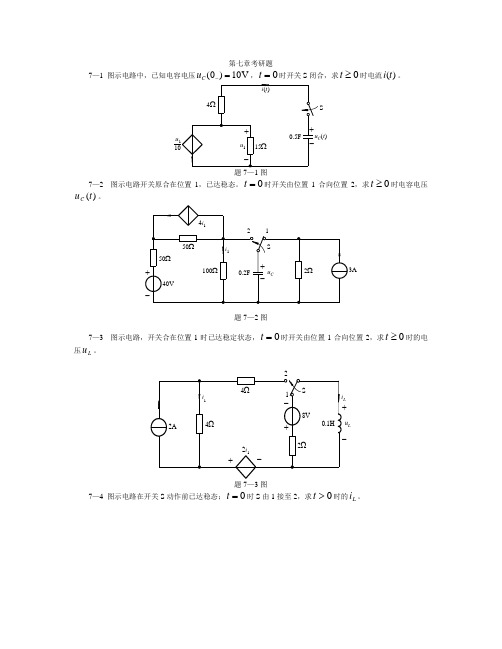
电路原理第五版 第七章考研题

电路原理第五版 第七章考研题

第七章考研题7—1 图示电路中，已知电容电压(0)10V C u -=，0=t时开关S 闭合，求0≥t 时电流)(t i 。

+-+-S0.5Fi (t )u 14Ω15Ωu C (t )u 110题7—1图7—2 图示电路开关原合在位置1，已达稳态。

0=t时开关由位置1合向位置2，求0≥t时电容电压)(t u C 。

+-+-0.2FS123Ai 14i 140V50Ω50Ω100ΩuC 2Ω题7—2图7—3 图示电路，开关合在位置1时已达稳定状态，0=t 时开关由位置1合向位置2，求0≥t 时的电压L u 。

+-+-+-2AS 28V0.1H1i 12i 14Ω4Ω2Ωu Li L题7—3图7—4 图示电路在开关S 动作前已达稳态；0=t时S 由1接至2，求0>t 时的L i 。

+-+-6V4V12S 2Ω0.2Fi L 1H(t = 0)题7—4图7—5 图示电路中，已知S 10()i t ε=A ，Ω=11R ，Ω=22R ，F μ1=C ，(0)2V C u -=，25.0=g S 。

求全响应)(1t i 、)(t i C 、)(t u C 。

+-+-i Si 1R 1u 1R 2gu 1i Cu CC题7—5图7—6 电路如图所示，当：（1）S()A i t δ=，0)0(=-C u ；（2）S ()A i t δ=，(0)1V C u -=；（3）S 3(2)A i t δ=-，(0)2V C u -=时，试求响应)(t u C 。

+-i S1k Ω2k Ω3 F u Cμ题7—6图7—7 图示电路中，S1()V u t ε=，S25()V u t ε=，试求电路响应)(t i L 。

+-+-u S1u S21Ω2Ω3Ωi L4H题7—7图7—8 图示电路中，电源S[50()2()]V u t t εδ=+，求0>t 时电感支路的电流)(t i 。

+-u S10Ω10Ωi0.1H题7—8图7—9 图示电路中，5S G =，0.25H L =，1F C =。

电路第五版 罗先觉 邱关源 课件(第七章)课件

电路第五版 罗先觉 邱关源 课件(第七章)课件

2
零输入响应：仅由电路初始储能引起的响应。
（输入激励为零） 零状态响应：仅由输入激励引起的响应。 （初始储能为零）
1. RC电路的放电过程：
如右图，已知uc(0-)=U0，S 于t=0时刻闭合，分析t≧0 时uc(t) 、 i(t)的变化规律。 +
i(t)
S uc(t) R
+ uR(t) -
(a)
i ()=12/4=3A
例3：如图(a)零状态电路，S于t=0时刻闭合，作0+图 并求ic(0+)和uL(0+)。 S Us ic
+ uc -
R2 L
S
↓iL
ic(0+) C
Us R1
R2 L
C R1
+ uL -
+ uL(0+) -
(a) 解: ① t<0时，零状态 →uc(0-)=0 iL(0-)=0 ② 由换路定理有：uc(0+)= uc(0-) =0 iL(0+)= iL(0-) =0 作0+图： 零状态电容→零值电压源 →短路线 零状态电感→零值电流源 →开路 ③ 由0+图有：ic(0+)=Us/R1 uL(0+)=uR(0+)=Us
uc(0+)= uc(0-) =8V
② 由换路定理有： iL(0+)= iL(0-) =2A 作0+等效图（图b）
S i 12V + R3 Us
2 R1 + uc (a) + R2 5 ic + iL 12V uL 4 i(0+) Us
R1 +
5
ic(0+) 8V

电路分析基础第七章__二阶电路

电路分析基础第七章__二阶电路

第七章二阶电路重点要求:1. 理解二阶电路零输入响应过渡过程的三种情况;2. 了解二阶电路的阶跃响应和冲击响应。

3.学习数学中的拉普拉斯变换的定义、性质及反变换的方法;4.掌握用拉普拉斯变换求解电路的过渡过程的方法。

1§7-1 二阶电路的零输入响应二阶电路:由二阶微分方程描述的电路。

典型的二阶电路是RLC串联电路。

求全响应方法:1.经典法(时域分析法)全响应= 稳态分量(强制分量) + 暂态分量(自由分量)2.拉普拉斯变换法(频域分析法)2响应曲线:U 0u C , u L , i 0ωtiu Cu L§7-1 二阶电路的零输入响应220p ααω=−±−一. 问题的提出经典法解动态电路过渡过程存在的问题：对较复杂的电路，联立求解微分方程特别是定积分常数比较困难。

若激励不是直流或正弦交流时，特解不容易求得。

二. 拉氏变换法用积分变换的原理简化求解电路过渡过程时域电路解微分方程时域响应f(t)取拉斯变换复频域电路解代数方程复频域响应F(s)取拉斯反变换7.2 动态电路的复频域分析应用拉氏变换法进行电路分析称为电路的一种复频域分析方法，也叫运算法！是数学中的一种积分变换.优点：对复杂电路﹑无稳态情况﹑换路时出现强迫跃变等用拉氏变换法较经典法方便。

三. 拉普拉斯变换的定义设函数f(t)在0≤t ≤∞时有定义，则积分称为原函数f(t)的拉普拉斯变换（象函数）。

()dte tf s F st∫∞−−=0)(式中s=σ+ j ω----复频率。

单位：熟悉的变换:相量法⎩⎨⎧=∫∞+∞−)s (21)(ds e F j t f stj c j c π反变换正变换ZH1.象函数F (s)存在的条件：∞<∫∞−−dt et f st0)(说明：电路分析中的函数都能满足上述条件。

2. 在电路中积分的下限定义为“0-”, 更有实际意义(将奇异函数也包括在内)。

[][]⎩⎨⎧==−)( )()( )( S F t f t f S F 1简写正变换反变换在电路分析中通常直接查表得到。

《电路》第五版 课件 第7章

− 1 t RC
c
全解
uc = uc′ + uc′′ = U s + Ae
由初始条件u 确定积分常数A 由初始条件 c(0+)=U0确定积分常数
uc (0+ ) = A + U s = U 0
∴ A = U0 − U s
− 1 t RC
uc (t ) = U s + (U 0 − U s )e
强制分量 稳态分量） （稳态分量）
1 t = iL (0− ) + ∫ u (ξ )dξ L 0−
Ψ=LiL
ψ = ψ (0− ) + ∫ u (ξ )dξ
0−
t
当u(ξ) 为有限值时 iL(0+)=iL(0-) Ψ(0+)=Ψ(0-)
∫0
0+
−
u (ξ )dξ → 0
磁链守恒
换路定理
uc(0+)=uc(0-) q(0+)=q(0-) iL(0+)=iL(0-) Ψ(0+)=Ψ(0-)
t
uc(0-)
换路定理
t =0+等 等 效电路
uc(0+)
ic(0+)
(1)由t=0-电路求uc(0-) 电路求 (1)由 电路 uc(0-)=8V ic(0-)=0≠ic(0+) (2)由 电阻(2)由换路定理
电路
uc(0+)=uc(0-)=8V
电阻 (0 ) ic + 电路
电路求 (3)由 (3)由t=0+电路求ic(0+)
思考题： 思考题：含有两个储能元件的电路
求iC(0+)和uL(0+) 和

电路原理 第五版 第五版 第七章(3)

(3)求通解 求通解 特征方程为： 特征方程为： 特征根为： 特征根为：
2
P + 200P + 20000 = 0
2
P= -100 ± j100
∴i = 1 + Ae
(4)定常数 定常数
−100t
sin(100t +ϕ)
ϕ = 45o A = 2
1 + Asinϕ = 2 ← iL (0+ ) + 100Acosϕ −100Asinϕ = 0 ← uL(0 )
(3)
uc = Ae−25t sin(139t +θ ) uc (0+ ) = 25 Asinθ = 25 139cosθ − 25sinθ = − 5 duc c = −5 10−4 dt 0 A = 355 ，θ = 176
uc 355 25 0
uc = 355e−25t sin(139t +1760 )V
U0 A= sin β
ω，ω０，δ间的关系 间的关系: 间的关系
ω ，β = arctg δ
ω0
ω β δ
ω sin β = ω0
ω0 −δ t uc = U0e sin(ωt + β ) ω
ω0 A = U0 ω
ω0 uc是其振幅以± U0为包线依指数衰减的正 弦函数。 弦函数。 ω
t=0时 uc=U0 时
t t=0+ ic=0 , t=∞ i c=0 ∞ ic>0 t = tm 时ic 最大 0< t < tm i 增加 uL>0 增加, i 减小 uL <0 减小,
duc − U0 p1t p2t ic = −C (e − e ) = dt L(P − P ) 2 1

电路分析基础第五版第7章


t1
uC (t1 ) duC (t)
dt tt1

U0e
1
U
0e

t1

在放电过程中，电容不断放出能量为电阻所 消耗；最后，原来储存在电容的电场能量全部为 电阻吸收而转换成热能。
时间常数愈小，放电过程愈快；反之，则愈慢。
二、RL电路的零输入响应
t0 iL(0)I0 初始条件
d 2 d u C 2 (tt)R L dd C ( u t)tL 1u C C (t)L 1u C s(t)
当求出uC(t)后，可应用元件的伏安关系求出电路中 其它元件的响应
i(t) C duC(t) dt
uR(t)R(it)RC dd C u(tt) uL(t)Ldd(it)tLC d2d uC 2t(t)
Req60 80 /210 0
R eC q 1 0 0 .0 0 2 1 6 0 2 s
i(0 ) 12 /10 0 1 0 .2 A u 0 (0 ) ( 1 .2 /2 ) 6 0 3V 6
故 i(t)1 .2 e 0 .5 160 tA t0
i(t) i(0 )e 1e 530 mA t 0
50 3
100
u (t)L dd i t2.5e130 tV 0 t0
§7-3 一阶电路的零状态响应
零状态响应：动态电路仅由外施激励引起的响应。
一、RC电路的零状态响应
在t=0时开关打开，电流
+ iC
iR
源与RC电路接通，引起 uC变化，产生响应。
§7-2 一阶电路的零输入响应 零输入响应：动态电路在没 有外施激励时,由动态元件的 初始储能引起的响应。
一、RC电路的零输入响应

电路第五版邱关源课件 第七章


1 C

t RC
e
t 0
t RC
C
1 C
+ uc
-
uc R

1 RC
uc ( 0 )
t 0
1 C
e
uC
uc
1 C

t RC
注意
e d uc dt
(t )
1 RC

t RC
t 0
e
iC
ic C
(t )
(t )
1 RC
1
t
例2
R
+ uL iL (0 ) 0
f(0)(t)



同理有：
f ( t ) ( t t 0 ) d t f ( t 0 )
(t)
(1) f(0)
f(t) t
* f(t)在 t0 处连续
0
二. 单位冲激响应
(t)
h(t)
零状态
1. 冲激函数作用于储能元件 当把一个单位冲激电流 i ( t ) （其单位为A）加到初始电 压为零且C=1F 的电容上，则电容电压u c为
dt 0
0

uc R
dt 0 ( t ) dt
0

=0
=1
uc (0 )

C [ u c ( 0 ) u c ( 0 )] 1
1 C
uC (0 )

电容中的冲激电流使电容电压发生跳变
b. t > 0+ 零输入响应（RC放电）
ic R

uc
ic
4. 单位冲激函数δ(t)对时间的积分等于单位阶跃函数ε(t)，即
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
本章主要讨论一阶和二阶电路的时域分析。首先建立动态电路的相关概念，如换路、瞬态、稳态，以及零输入、零状态和全响应等。对于由RLC组成的二阶电路，深刻理解了其不同动态响应的形式和物理机理，以及与RLC元件参数之间的关系。同时，强调了牢固掌握动态电路初始条件求法的重要性，并介绍了如何运用‘三要素’法分析一阶动态电路，以及二阶动态电路的分析方法。通过引例闪光灯电路，进一步阐释了电路构成、工作方式和元件参数选择的实际应用。在详细解析动态电路的方程和初始条件时，阐述了过渡过程、换路的概念，以及换路定律和初始条件的求解方法，包括电容电压和电立初始条件。这些内容对于理解和掌握电路分析的基础知识和实践应用具有重要意义。