下载文档原格式
第四章电路定理4-1应用叠加定理求图示电路中电压U ab。
1'-.1e」AU ni =3si ntVU ab C)= 汉1 = sin tV2+1题解4-1图对(b)图，应用电阻分流公式有_t e i _ 1 113 2 1所以1e_t V5U ab =Uab°)+Uab«)=Sint + 亠95丄丄1'Juab题4-1图解：画出两个电源单独作用时的分电路如题解对(a)图应用结点电压法可得：4-1图所示5sin tU ni解得:、+ r -5sin tV L1。
-L'bU ab2 " 1I'? 2门⑻a +e A(b)U ab------ a +i1 1 U ab 24-2应用叠加定理求图示电路中电压 u+136V解：画出电源分别作用的分电路图对(a)图应用结点电压法有136 50U ni 二8+2 10解得:u ^-u n ^82.667V对(b)图，应用电阻串并联化简方法，可得：2』8+空©10 40 u * 2 二处一8V23所以，由叠加定理得原电路的u 为 4-3应用叠加定理求图示电路中电压 U 218+2 40 10 丿400丿50V题4-2图16 V 2 33门解：根据叠加定理，作出电压源和电流源单独作用时的分电路，受控源均保留在分电路中。
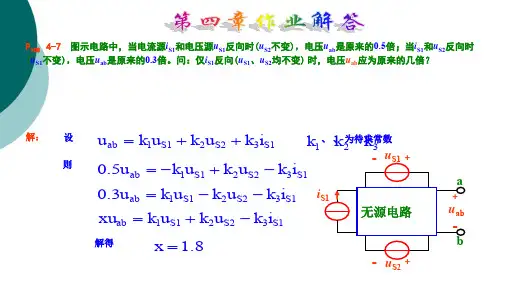
题解4-3图（a）图中12i10.5A4所以根据KVL有u2^-3 2i11 2 =-1V（b）图中ii（2）=0u22 = 3 3 = 9V故原电路电压u2 = u2f）+ u2（2）= 8V4-4图示电路中，当电流源i si和电压源U si反向时（U s2不变），电压u a b是原来的0.5 倍；当电流源i si和电压源U si反向时（U si不变），电压U ab是原来的0.3倍。
问：仅i si 反向时（U si，u s2不变），电压U ab应为原来的多少倍？解：根据叠加定理，设响应1 U ab = K i i slK 2U SI k 3U s2式中K i , K 2 , k 3为未知的比例常数，将已知条件代入上式，得2°.5U ab = -K/si - K 2us1 k 3us23 0.3U ab—K i i si 心人1 弋匕24xu ab =-K i i si ©U sik a U s2将(i),(2) ,(3)式相加，得5i.8U ab 一K i i siK 2U si k 3U s2因此求得X h.84-5图示电路U si =i0V ，U s2 =i5V ，当开关S 在位置i 时，毫安表的读数为r-40mA ;当开关S 在位置2时，毫安表的读数为1：：上-60mA 。
电路分析第五版答案第一章简介1.1 电路分析的重要性•电路分析是电气工程的基础课程之一，是理解电路原理和设计电路的关键。
•电路分析可以帮助我们了解电流、电压、功率等基本概念，并掌握电路元件的特性和相互关系。
1.2 本书的结构和内容本书共分为八个章节：1.第一章简介2.第二章基本电路定律3.第三章电阻电路4.第四章电容电路5.第五章电感电路6.第六章交流电路分析7.第七章双端口网络8.第八章共模与差模分析第二章基本电路定律2.1 基本电路定律的概述电路中的电压和电流遵循一些基本定律，包括：•基尔霍夫电流定律（KCL）•基尔霍夫电压定律（KVL）•电阻定律（Ohm’s Law）2.2 基尔霍夫电流定律（KCL）根据基尔霍夫电流定律，任何节点处的电流代数和必须等于零。
这可以用公式表示为：$$\\sum_{i=1}^n I_i = 0$$2.3 基尔霍夫电压定律（KVL）根据基尔霍夫电压定律，电路中任何回路的电压总和必须等于零。
这可以用公式表示为：$$\\sum_{i=1}^n V_i = 0$$2.4 电阻定律（Ohm’s Law）根据电阻定律，电阻的电压和电流之间存在线性关系。
这可以用公式表示为：V=VV其中，V表示电阻两端的电压，I表示通过电阻的电流，R 表示电阻的阻值。
第三章电阻电路3.1 电阻的基本性质•电阻是电路中常见的元件，用于限制电流的流动。
•电阻的阻值可以通过颜色代码或万用表进行测量。
3.2 串联电阻和并联电阻•串联电阻是将电阻依次连接在一起，电流从一个电阻流向下一个电阻。
•并联电阻是将电阻并排连接在一起，电流可以通过多个路径流动。
3.3 电阻网络的简化•电阻网络可以用串联和并联的组合来简化。
•通过串并联电阻的变换，可以将复杂的电阻网络简化为更简单的形式。
第四章电容电路4.1 电容的基本性质•电容是一种能够存储电荷的元件。
•电容的电压和电荷之间存在线性关系。
4.2 电容充放电过程•当电容器被连接到电池正极时，电容开始充电。
4-2．5μF 电容的端电压如图示。
（1）绘出电流波形图。
（2）确定2μs t =和10μs t =时电容的储能。
解：（1）由电压波形图写出电容端电压的表达式：10 0μs 1μs10 1μs 3μs ()1040 3μs 4μs 0 4μs t t t u t t t t≤≤⎧⎪≤≤⎪=⎨-+≤≤⎪⎪≤⎩ 式中时间t 的单位为微秒；电压的单位为毫伏。
电容伏安关系的微分形式：50 0μs 1μs 0 1μs 3μs()()50 3μs 4μs 0 4μs t t du t i t C t dt t<<⎧⎪<<⎪==⎨-<<⎪⎪<⎩上式中时间的单位为微秒；电压的单位为毫伏；电容的单位为微法拉；电流的单位为毫安。
电容电流的波形如右图所示。
（2）电容的储能21()()2w t Cu t =，即电容储能与电容端电压的平方成正比。
当2μs t =时，电容端电压为10毫伏，故：()()22631010μs 11()5101010 2.510J 22t w t Cu ---===⨯⨯⨯⨯=⨯当10μs t =时，电容的端电压为0，故当10μs t =时电容的储能为0。
4-3．定值电流4A 从t=0开始对2F 电容充电，问：（1）10秒后电容的储能是多少？100秒后电容的储能是多少？设电容初始电压为0。
解：电容端电压：()()()00110422t tC C u t u i d d t C τττ+++=+==⎰⎰；()1021020V C u =⨯=； ()1002100200V C u =⨯=()()211010400J 2C w Cu ==； ()()2110010040000J 2C w Cu ==4-6．通过3mH 电感的电流波形如图示。
（1）试求电感端电压()L u t ，并绘出波形图；（2）试求电感功率()L p t ，并绘出波形图；（3）试求电感储能()L w t ，并绘出波形图。
