当前位置：文档之家 › 电路分析基础习题第五章答案

电路分析基础习题第五章答案

  • 格式：doc
  • 大小：778.00 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

《电路分析基础》习题参考答案

《电路分析基础》习题参考答案

《电路分析基础》各章习题参考答案第1章习题参考答案1-1 (1) SOW; (2) 300 V、25V,200V、75V; (3) R=12.50, R3=1000, R4=37.5021-2 V =8.S V, V =8.S V, V =0.S V, V =-12V, V =-19V, V =21.S V U =8V, U =12.5,A mB D 'AB B CU =-27.S VDA1-3 Li=204 V, E=205 V1-4 (1) V A=lOO V ,V=99V ,V c=97V ,V0=7V ,V E=S V ,V F=l V ,U A F=99V ,U c E=92V ,U8E=94V,8U BF=98V, u cA=-3 V; (2) V c=90V, V B=92V, V A=93V, V E=-2V, V F=-6V, V G=-7V, U A F=99V, u c E=92V, U B E=94V, U BF=98V, U C A =-3 V1-5 R=806.70, 1=0.27A1-6 1=4A ,11 =llA ,l2=19A1-7 (a) U=6V, (b) U=24 V, (c) R=SO, (d) 1=23.SA1-8 (1) i6=-1A; (2) u4=10V ,u6=3 V; (3) Pl =-2W发出，P2=6W吸收，P3=16W吸收，P4=-lOW发出，PS=-7W发出，PG=-3W发出1-9 l=lA, U5=134V, R=7.801-10 S断开：UAB=-4.SV, UA0=-12V, UB0=-7.2V; S闭合：12 V, 12 V, 0 V1-12 UAB=llV / 12=0.SA / 13=4.SA / R3=2.401-13 R1 =19.88k0, R2=20 kO1-14 RPl=11.110, RP2=1000第2章习题参考答案2-1 2.40, SA2-2 (1) 4V ,2V ,1 V; (2) 40mA ,20mA ,lOmA 2-3 1.50 ,2A ,1/3A2-4 60 I 3602-5 2A, lA2-6 lA2-7 2A2-8 lOA2-9 l1=1.4A, l2=1.6A, l3=0.2A2-10 11=OA I l2=-3A I p l =OW I P2=-l8W2-11 11 =-lA, l2=-2A I E3=10V2-12 11=6A, l2=-3A I l3=3A2-13 11 =2A, l2=1A ,l3=1A ,14 =2A, l5=1A2-14 URL =30V I 11=2.SA I l2=-35A I I L =7.SA2-15 U ab=6V, 11=1.SA, 12=-lA, 13=0.SA2-16 11 =6A, l2=-3A I l3=3A2-17 1=4/SA, l2=-3/4A ,l3=2A ,14=31/20A ,l5=-11/4A12-18 1=0.SA I l2=-0.25A12-19 l=1A32-20 1=-lA52-21 (1) l=0A, U ab=O V; (2) l5=1A, U ab=llV。

【免费下载】电路分析基础 上海交通大学出版社习题答案-第5章和第8章

【免费下载】电路分析基础 上海交通大学出版社习题答案-第5章和第8章

第5章5.1解：s /rad LC 710811-⨯==ωHz LC f 571021082121⨯≈⨯⨯==-ππA .R U I 050108170-⨯==V L I U CO 2500==ω5.2解：(1)Ω61150252===max P U R H .C L 01601010250011622=⨯⨯==-ω(2)2406110102500250062=⨯⨯⨯==-R L Q ω通频带: 42102402500.Q ===ωω∆5.3解：(1)Ω3400==max I U R (2)H I U L L 1200010150300300=⨯⨯==-ω(3)F .L C μω250120==(4)15203000===S L U U Q 5.4解：(1)mH ...I U L L 05010591220100600=⨯⨯⨯==πω Ω100==I U R (2)5021000===S L U U Q(3)4010183⨯==.Qf f ∆5.5解：(1)MHz LC f 221==π (2)2402010641022660.R L Q =⨯⨯⨯⨯==-πω(3)A .R U I s 202040===(4)V .QU U S C 81600==5.6解：(1)Ωk R 51010503=⨯=- (2)F .U I C C C μω2505000501060300=⨯⨯==- (3)H ..C L 16010250500011622=⨯⨯==-ω (4)2560.CR Q ==ω5.7解：电流表读数为零，说明发生了并联谐振。

(1)F .L C μω530103002500113220=⨯⨯==-(2)︒∠=︒∠⨯==605339602555./R I U (3)︒∠==60255/I I R ︒-∠=⨯⨯︒∠==-3053010300250060533930.j .L j U I L ω ︒-∠-=-=30530.I I L C 5.8解：s/rad LC 5100010==ω 5100.CR Q ==ω s /rad Q 40010==ωω∆5.9解：(1)501020101360=⨯⨯==f f Q ∆(2)H .Q R L 183501021010630≈⨯⨯⨯==πω(3)F R Q C μπω796101010250360≈⨯⨯⨯==5.10解：(1)Ω010*********.I P R S ≈⨯==-(2)V ..R I U S 0202010=⨯==(3)nH ..I U L L 05010220002060≈⨯⨯==ω(4)mF .U I C L 510202020060≈⨯⨯==ω5.11 解：(1) 247pF 。

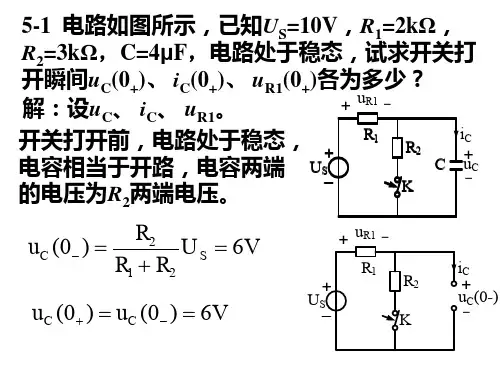
电路分析第五章答案

电路分析第五章答案

24 iL (0 ) iL (0 ) 3A 26
24 6 iL ( ) i ( ) 2.4A 6 6 // 2 6 2 t iL (t ) iL () [iL (0 ) iL ()]e
L 2.5 103 103 s R 2.5
R2 uC (0 ) U S 6V R1 R2
+ uR1 + R1
−
R2 K
uC (0 ) uC (0 ) 6V
US
iC + uC(0-)
−
用6V电压源替代电容，求解iC(0+)、 uR1(0+)
uR1 (0 ) U S 6 4V
u R1 (0 ) 4 iC (0 ) 2mA US+ R1 2
51电路如图所示已知u3kc4f电路处于稳态试求开关打开瞬间ur1开关打开前电路处于稳态电容相当于开路电容两端的电压为r52电路如图所示已知u6l5mh电路处于稳态试求开关打开瞬间ir1开关打开前电路处于稳态电感相当于短路电感电流等于电阻r53电路如图所示开关未动之前电路处于稳定状态
5-1 电路如图所示，已知US=10V，R1=2kΩ， R2=3kΩ，C=4μF，电路处于稳态，试求开关打 开瞬间uC(0+)、 iC(0+)、 uR1(0+)各为多少？ uR1 − + 解：设uC、 iC、 uR1。 iC 开关打开前，电路处于稳态， + R1 R2 + C u C 电容相当于开路，电容两端 US − K 的电压为R2两端电压。
t

400 t
)V
i(t ) i() [i(0 ) i()]e

40e 400 t mA

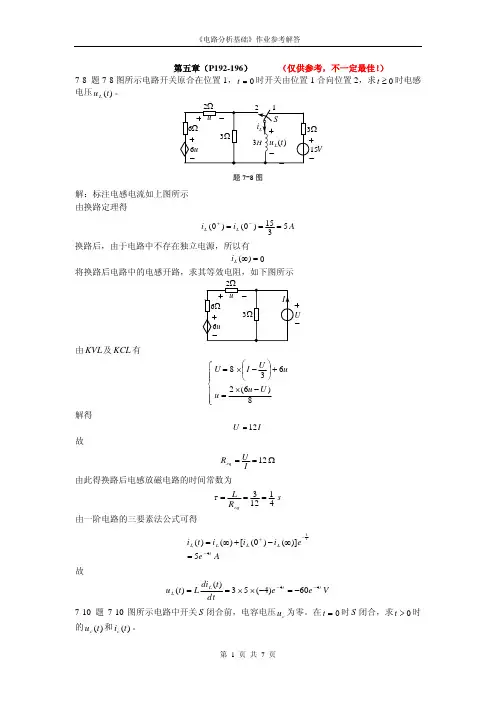
电路作业参考解答(第五章)

电路作业参考解答(第五章)
S
8i
i 2Ω
20V
i c (t )
2Ω
0.1F
u c (t )
题 7-13 图
解：由换路定理有
u c ( 0 + ) = u c (0 − ) = 0
换路后，将电容开路，求其戴维宁等效电路
1. 求开路电压 u oc
第 3 页 共 7 页
《电路分析基础》作业参考解答
8i
i 2Ω
20V
2Ω
uoc
2Ω 16i
故 i c (t ) = C = e −10 t
t −τ
(
)
d u c (t ) = 10 × 10 − 6 × 10 × ( −1) × ( −10)e −10 t dt mA
7-11 题 7-11 图所示电路中开关 S 打开前已处稳定状态。 求 t ≥ 0 时的 u L (t ) t = 0 开关 S 打开，
换路后，将电容开路，求其戴维宁等效电路
2. 求开路电压 u oc
50Ω 50Ω
40V
200i1
i1
100Ω
o
uoc
o
如上图所示，由 KVL 有
(50 + 50) i1 + 200i1 + 100i1 = 40
解得 i 1 = 0.1 A 。 故
u oc = 100i1 = 10 × 0.1 = 10 V
解得
U = 12 I
故
R eq = U = 12 Ω I
由此得换路后电感放磁电路的时间常数为
τ= L = 3 =1 s
R eq 12 4
由一阶电路的三要素法公式可得
i L (t ) = i L (∞) + [i L (0 + ) − i L (∞ )] e = 5e − 4t A

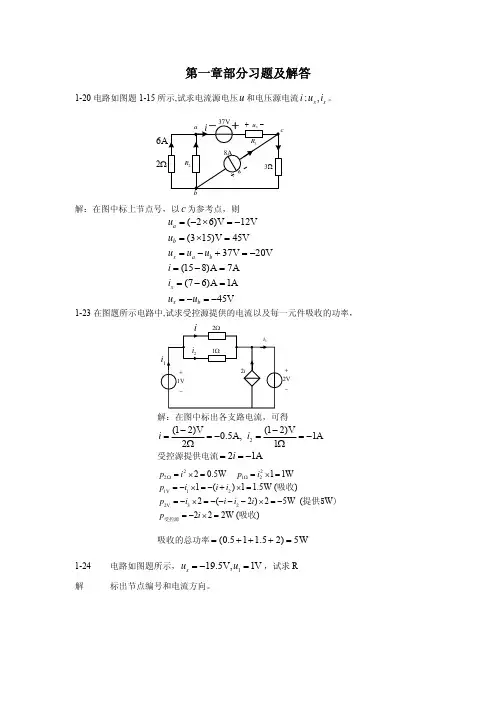
电路分析基础第四版课后习题答案

电路分析基础第四版课后习题答案
1-23 在图题所示电路中,试求受控源提供的电流以及每一元件吸收的功率，
i
i1
+ 1V −
2Ω
i3
i2
1Ω
2i
+ 2V −
解：在图中标出各支路电流，可得
(1 − 2)V (1 − 2)V = −0.5A, i2 = = −1A 2Ω 1Ω 受控源提供电流 = 2i = −1A i=
p2 Ω = i 2 × 2 = 0.5W
为确定 R，需计算 i4 ，
uce = ucd + ude = 0 ⇒ ude = −ucd = −10u1 = −10V
故
i3 =
udc = −2.5A, i4 = is − i3 = (−3.5 + 2.5)A = −1A 4 R = 0Ω 由此判定
1-33
试用支路电流法求解图题所示电路中的支路电流 i1 , i2 , i3 。
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2
⎧25i1 − 20i2 − 5i3 = 50 ⎪ 代入并整理得： ⎨−5i1 + 9i2 − 4i3 = 0 解得 ⎪−5i − 4i + 10i = 0 2 3 ⎩ 1
受控源电压 受控源功率
⎧i1 = 29.6A ⎨ ⎩i2 = 28A
i2
3Ω
i3
gu
2−5
解
设网孔电流为 i1 , i2 , i3 ,则 i3 = − gu A = −0.1u A ,所以只要列出两个网孔方程
27i1 − 18i2 = 42 −18i1 + 21i2 − 3(−0.1u A ) = 20
因 u A = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20

大学电工电子基础习题参考答案：第5章习题习题参考答案

大学电工电子基础习题参考答案：第5章习题习题参考答案

第五章习题参考答案5.1 题5.1的图所示的是三相四线制电路，电源线电压l U ＝380V 。

三个电阻性负载接成星形，其电阻为1R =11Ω，2R =3R =22Ω。

(1)试求负载相电压、相电流及中性线电流，并作出它们的相量图；(2)如无中性线，求负载相电压及中性点电压；(3)如无中性线，当L1相短路时求各相电压和电流，并作出它们的相量图；(4)如无中性线，当L3相断路时求另外两相的电压和电流；(5)在(3)，(4)中如有中性线，则又如何?1L 2L 3L N题5.1的图解： ○1各相负载两端电压都等于电源相电压，其值为：V V U U l P22033803===。

各负载相电流分别为：()()AI I I I I I A R UI A R U I A R U I N P P P 1030cos 30cos 30sin 30sin 10,10,202232132332211=︒-︒++︒-︒-=======相量图如图（b ）所示。

○2因为三相电源对称，而三相负载不对称时，由于无中性线，将使电源和负载中点之间的电位差不为零，而产生中性点位移。

设 V U U ︒∠=011 ()()()V V U U U V V U U U VV U U U V V R R R R U R U R U U NN N N N N N N ︒∠=︒∠-︒∠=-=︒-∠=︒∠-︒-∠=-=︒∠=︒∠-︒∠=-=︒∠=++︒∠+︒-∠+︒∠=++++=131252055120220131252055120220016505502200552212211112212022022120220110220111''''3'32'21'1321332211○3若无中性线，1L 相短路，此时电路如图（c ）所示，此时1L 相的相电压01=U ，2L 相、3L 相的相电压分别等于2L 、1L 之间、3L 、1L 之间的线电压，所以有：V U U V U U ︒∠==︒-∠=-=150380,150380313122 各相电流为：()()A A I I IV R U I VR U I ︒∠=︒∠+︒-∠-=+-=︒∠==︒-∠==0301503.171503.171503.171503.17321333222 相量图如图（d ）所示○4若无中线，3L 相断路，电路如图（e ）所示，1L ，2L 两相成了串联电路： V V R I UV V R I U AA R R U I I ︒∠=⨯︒∠=∙=︒∠=⨯︒∠=∙=︒∠=+︒∠=+==3025322305.113012711305.11305.11221130380222111211221 ○5当有中性线，1L 相短路或3L 相断路，其他相电压、电流均保持不变。

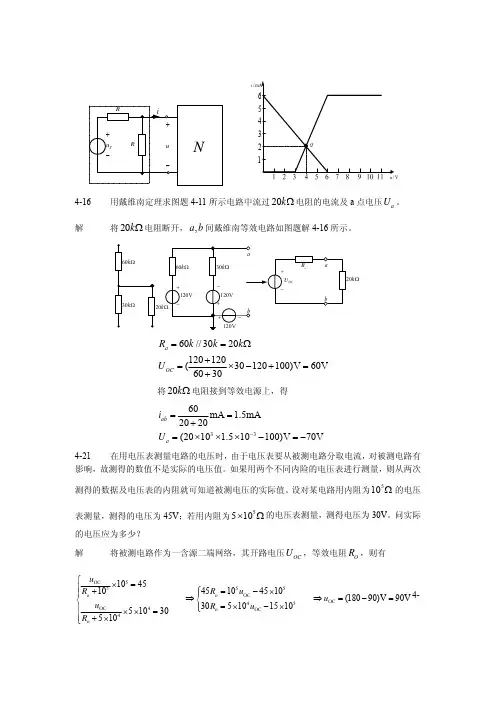
电路分析基础第四版课后习题第四章第五章第六章答案

电路分析基础第四版课后习题第四章第五章第六章答案

/i4-16 用戴维南定理求图题4-11所示电路中流过20k Ω电阻的电流及a 点电压。

a U 解将电阻断开，间戴维南等效电路如图题解4-16所示。

20k Ω,a bk Ω60//3020120120(30120100)V 60V6030a OCR k k k U ==Ω+=×−+=+ 将电阻接到等效电源上，得20k Ω3360mA 1.5mA2020(2010 1.510100)V 70V ab a i U −==+=×××−=− 4-21 在用电压表测量电路的电压时，由于电压表要从被测电路分取电流，对被测电路有影响，故测得的数值不是实际的电压值。

如果用两个不同内险的电压表进行测量，则从两次测得的数据及电压表的内阻就可知道被测电压的实际值。

设对某电路用内阻为的电压表测量，测得的电压为45V ；若用内阻为510Ω5510×Ω的电压表测量，测得电压为30V 。

问实际的电压应为多少？ 解将被测电路作为一含源二端网络，其开路电压，等效电阻OC U O R ，则有5OC 555o o OC OC 454OCo OC 4o 10451045104510(18090)V 90V 30510151051030510u R R u u u R u R ⎧×=⎪⎧+=−×⎪⎪⇒⇒=⎨⎨=×−×⎪⎪⎩××=⎪+×⎩−=4-28 求图题4-20所示电路的诺顿等效电路。

已知：12315,5,10,R R R =Ω=Ω=Ω。

10V,1A S S u i ==解对图题4-20所示电路，画出求短路电流和等效内阻的电路，如下图所示SC i对左图，因ab 间短路，故0,0i i α==，10A 0.5A 155SC i ==+ 对右图，由外加电源法，106ab R α=Ω− 4-30 电路如图题4-22所示。

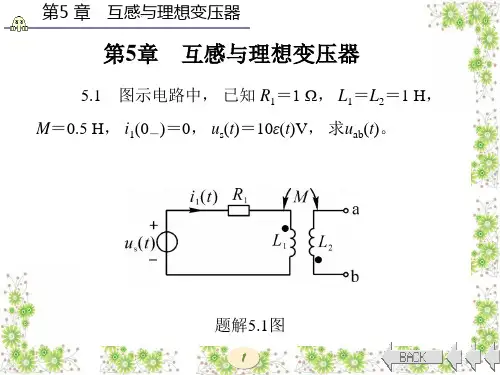
电路分析基础(第四版)张永瑞答案第5章

电路分析基础(第四版)张永瑞答案第5章
40
第5 章 互感与理想变压器 解 自耦变压器对求 U1、I1、U2、I2 来说可以等效为题解
5.9图所示的理想变压器。 设a端到c端的匝数为N1， b端到c端 的匝数为N2， 显然， 有
N1 U1 220 1.1 N2 U2 200
41
第5 章 互感与理想变压器
设 U2 2000 V ， 则
题解5.7图
36
第5 章 互感与理想变压器 5.8 求题5.8图所示的两个电路从ab端看的等效电感Lab。
题5.8图
37
第5 章 互感与理想变压器 解 应用互感T形去耦等效， 将题5.8图(a)、 题5.8图(b)分
别等效为题解5.8图(a)、 题解5.8图(b)。 图 (a)： Lab=1+2∥2=2 H 图 (b)： Lab=1+［4+(－1)］∥(2+4)+3=6 H
题解5.6图
33
第5 章 互感与理想变压器 5.7 题5.7图所示为全耦合空芯变压器， 求证：当次级短
路时从初级两端看的输入阻抗Zin＝0； 当次级开路时从初级两 端看的输入阻抗Zin＝jωL1。
题5.7图
34
第5 章 互感与理想变压器
证明 k=1知互感 M L1L2 。 画T形去耦等效电路并
R r1 r2 Z cosjz 300.8 24
阻抗Z中的电抗即相串联的两个互感线圈等效电感的感抗
X L Z sinjz 30 1 0.82 18
等效电感
L X L 18 57.3mH
2 f 100
25
第5 章 互感与理想变压器
由于是顺接，
0.5
d i1 dt
（2）

电路分析基础(英文版)课后答案第五章

电路分析基础(英文版)课后答案第五章
Z
i1 + i2 = i DE 5.5 v1 = 0:5 £ 10
6 t 0+
240 £ 10¡6 e¡10x dx ¡ 10 = ¡12e¡10t + 2 V
t 0+
v2 = 0:125 £ 106 v1 (1) = 2 V; W =
·
Z
240 £ 10¡6 e¡10x dx ¡ 5 = ¡3e¡10t ¡ 2 V
Z
v (t) v (0+ )
155
Z dy R t dx =¡ y L 0+
¯v(t) µ ¶ ¯ R ¯ ln y ¯ =¡ t +
v (0 )
L
v (t) R =¡ t ln + v (0 ) L v (t) = v (0 )e
+ ¡(R=L)t
"
#
µ

;
Vs v (0 ) = ¡ Io R = Vs ¡ Io R R
60(240) = 48 mH 300 [b] i(0+ ) = 3 + ¡5 = ¡2 A 125 Z t (¡0:03e¡5x ) dx ¡ 2 = 0:125e¡5t ¡ 2:125 A [c] i = 6 0+ 50 Z t [d] i1 = (¡0:03e¡5x ) dx + 3 = 0:1e¡5t + 2:9 A 3 0+ i2 = 25 Z t (¡0:03e¡5x ) dx ¡ 5 = 0:025e¡5t ¡ 5:025 A 6 0+
v (0+ ) = ¡9:6 + 38:4 = 28:8 V [b] v = 0 when 38:4e¡1200t = 9:6e¡300t

电路基础：第五章部分习题解

电路基础：第五章部分习题解

第五章5.1 如题5.1图所示电路，0<t 时已处于稳态。

当0=t 时开关S 打开,求初始值)0(+c u 和)0(+c i 。

解：V u u V u u s c 4)0()0(.4424)0(===+=-+-，所以因为电容是独立初始值。

开关断开后，,A i i u c c 8.0)0(,0)41()0()0(-==+∙+-++。

cu-cut<0,稳态c4开关断开后5.2 如题5.2图所示电路，0<t 时已处于稳态。

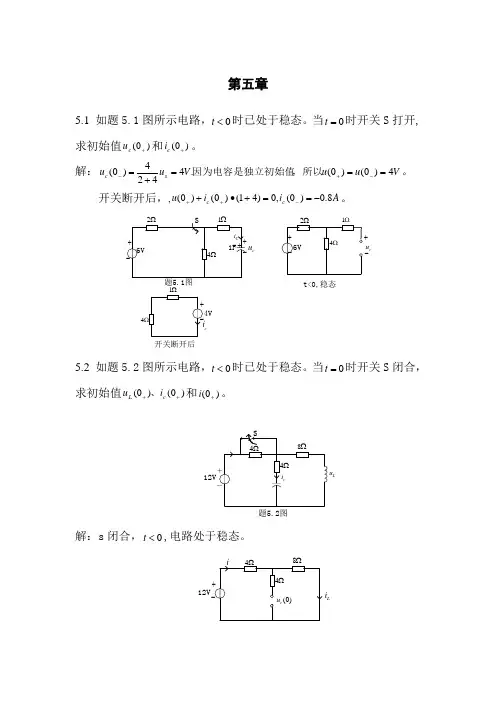
当0=t 时开关S 闭合，求初始值)0()0(++c L i u 、和)0(+i 。

Lu 题5.2图12V解：s 闭合，0<t ,电路处于稳态。

12VLiA i V u L c 18412)0(,812848)0(=+==⨯+=--, s 闭合后，独立初始值。

V u u c c 8)0()0(==-+,A i i L L 1)0()0(==-+.L uA i i c c 1)0(,1284==+⨯+， A i i i c 2)0(,1)0()0(=+=+++， V u u L L 4)0(,1218)0(==⨯+-+。

5.3 如题5.3图所示电路，0<t 时已处于稳态。

当0=t 时开关S 闭合求)0(+L i 和=t L dtdi 。

解：0=t 时，A i L 1)0(=-，S 闭合，A i L 1)0(=+，等效为b 图。

0442)1(4=⇒=+++i i i i ，0)0(=∴+L u ，00=+=t L dtdi ，A i L 1)0(=∴+，00=+=t L dtdi 。

iΩ题5.3图5.5 如题5.5图所示电路，0<t 时已处于稳态。

当0=t 时开关S 打开，求初始值)0(+c u 和)0(1+L i 、)0(2+L i 。

10VΩCu +-题5.5图解：0<t 时，V U c 6)0(=-，A i L 2)0(1=+，A i L 0)0(2=+； S 打开，V U c 6)0(=+，A Vi L 144)0(1=Ω=+，A i L 1)0(2=+。

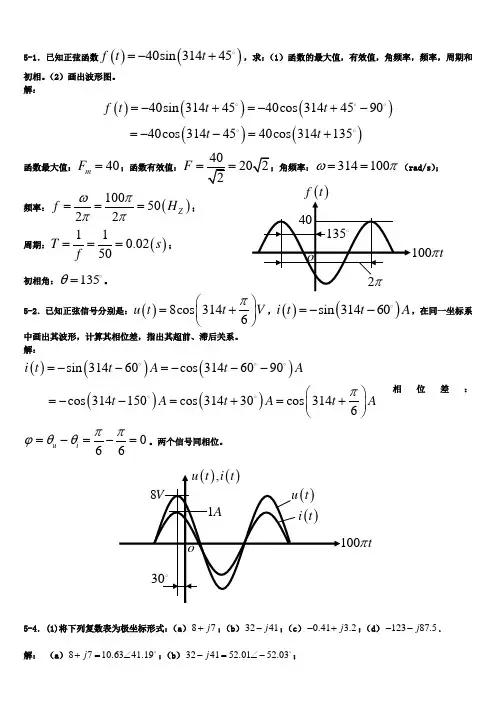
电路分析基础第五章答案

电路分析基础第五章答案

5-1．已知正弦函数()()40sin31445f t t=-+，求：（1）函数的最大值，有效值，角频率，频率，周期和初相。

（2）画出波形图。

解：()()()()()40sin3144540cos314459040cos3144540cos314135f t t tt t=-+=-+-=--=+函数最大值：40mF=；函数有效值：40F==314100ωπ==（rad/s）；频率：()1005022Zf Hωπππ===；周期：()110.0250T sf===；初相角：135θ=。

5-2．已知正弦信号分别是：()8cos3146u t t Vπ⎛⎫=+⎪⎝⎭，()()sin31460i t t A=--，在同一坐标系中画出其波形，计算其相位差，指出其超前、滞后关系。

解：()()()()()sin31460cos3146090cos314150cos31430cos3146i t t A t At A t A t Aπ=--=---⎛⎫=--=+=+⎪⎝⎭相位差：66u iππϕθθ=-=-=。

两个信号同相位。

5-4．(1)将下列复数表为极坐标形式：（a）87j+；（b）3241j-；（c）0.41 3.2j-+；（d）12387.5j--.解：（a）8710.6341.19j+=∠；（b）324152.0152.03j-=∠-；2πtπf t135tπ30（c ）0.41 3.2 3.22697.30j -+=∠；（d ）12387.5150.95144.6j --=∠-(2)将下列复数表为直角坐标形式：（a ）7.925.5∠；（b ）11.954.5∠-；（c ）22120∠；（d ）80150∠-. 解： （a ）7.925.57.13 3.40j ∠=+；（b ）11.954.5 6.919.69j ∠-=- （c ）221201119j ∠=-+；（d ）8015069.340j ∠-=--5-5．计算：(1) 615440760?∠-∠+∠-=；(2) ()()()()103456473?j j j j ++-+=；(3) 417590 2.540 2.130?j j ⎛⎫⎡⎤-++∠∠+∠-= ⎪⎣⎦⎝⎭解：(1)()()()()()6154407606cos156sin154cos 404sin 407cos607sin 606cos154cos 407cos606sin154sin 407sin 606.237.08j j j j j j j ∠-∠+∠-=+-++-=-++--=-(2)()()()()()()()()() 10345647310.4416.706.40351.347.233.697.61623.2010.44 6.4037.216.7051.3433.6923.207.61663.2011.15j j j j ++-+=∠∠∠-∠⨯⨯=∠+--=∠(3)()()(){}()()()()417590 2.540 2.1301745 2.5cos 40 2.1cos 30 2.5sin 40 2.1sin 3016 3.7340.557016903.7758.4844.23898.48j j j j j j j j ⎛⎫⎡⎤-++∠∠+∠- ⎪⎣⎦⎝⎭⎡⎤⎡⎤=--++-++-⎣⎦⎣⎦=-+=∠-∠=∠-5-8．已知元件A 的端电压：()()100030 ()u t t V =+，求流过元件A 的电流()i t 。

电路分析基础第5章习题答案

电路分析基础第5章习题答案
S1 3A 3Ω 0.5F 2Ω + uC 6Ω S2
i
3Ω + 3V

t=0-时，电容相当于开路，等效电路为
S1 3A 3Ω 0.5F 2Ω
i
3 6 u c (0 ) 3 6V 3 6 uc (0) uc (0) 6V
6Ω + uC(0-)
t =0+时，电容所在支路用电压源代替。等 效电路如下 i (0+)
R0 750// 1500 500
RC 500 50 106 0.025s
uc (t ) u (0 )e
t

54e

t 0.025
V
t0
t=20ms时
uc (0.02) 54e
0.02 0.025
54e 0.8 24.26V
1 2 1 Wc(t) cu c (t ) 50106 24.262 0.0147W 2 2
iL(∞)
iL (t ) iL () [iL (0) iL ()]e 0.2 [0.3 0.2]e
t
.2 0.5e
t

i(t ) i() [i(0) i()]e 0.3 [0.075 0.3]e
t

t
5mH
+ 9V
iL
9 30 iL (0 ) 0.3A 10 30 // 15 30 15 iL (0) iL (0) 0.3A
t=0+时，电感相当于电流源，等效电路为
i
i (0+)
10Ω 6V + 15Ω 30Ω
iL(0+)

电路分析课后习题第5章习题答案

电路分析课后习题第5章习题答案
t t
8isc − 4 × 2 = 2i1 isc = 1.2A i1 = 2 − isc
5-16 图示电路，在t<0已处于稳态，在t = 0时 图示电路， 已处于稳态， 已处于稳态 时 将开关S由1切换至 ，求i(0+)和u(0+)。 将开关 由 切换至2， 和 。 切换至
2
1 S t=0 2 5A 3
i
3 + 3V −
−
t=0-时，电容相当于开路，等效电路为 时 电容相当于开路，
S1 3A 3 0.5F 2 6 + uC(0-)
i
− 3× 6 u c (0 − ) = 3 × = 6V 3+ 6 uc (0+) = uc (0−) = 6V
i(0+) 2 + 12V 4 + u
−
−
12 4 i (0 + ) = + 3× = 4A 2+4 4+2 u (0 + ) = (4 − 3) × 4 = 4V
5-18电路如图所示，t<0时电路处于稳态，在 电路如图所示， 时电路处于稳态 时电路处于稳态， 电路如图所示 t = 0时将开关 闭合，求电容电压 C（t）。 时将开关S闭合 时将开关 闭合，求电容电压u ） S t=0 1 2 + 300µF µ uC 1A
t t t
τ
τ
τ
t 5-15图示电路，求电容电压 u（），≥ 0 。已知 图示电路， 图示电路 C t
u C 0 = 0V （）
i1 4 2A
4 0.01F + 2i1 − + uC
−
首先求出虚线左端的戴维南等效电路。 首先求出虚线左端的戴维南等效电路。

电路分析第五章习题解答

电路分析第五章习题解答

uL (t) 波形为
uL /V
0.5
0
1
2
3
4
t/s
-0.5
3、作用于 25μF 电容的电流如图题 5-3 所示，若 uc (0) = 0 ，试确定 t = 17ms 和 t = 40ms
时电容电压、吸收功率以及储能各为多少？
iC (mA) 20
10
0
10 20 30
t (ms)
图题 5-3
解：
∫ Q
− k1 cos t − k2 sin t − 2k1 sin t + 2k2 cos t + k1 cos t + k2 sin t = cos t
cos t(−k1 + 2k2 + k1 −1) + sin t(−k2 − 2k1 + k2 ) = 0
∴ k1 = 0
k2
=
1 2
∴
yp
(k)
=
t 3
iC
(ξ
)dξ
= 0 + 103 × 0 = 0V
波形为：
uC V
2 ×103
ts
−1
123
− 2 ×103
2、已知电感 L = 0.5H 上的电流波形如图题 5-2 所示。试求电感电压，并画出波形图。
iL (A) 1
0
12
3
t(s)
解：
−1 图题 5-2
Q
uL
=
L
diL (t) dtFra bibliotekt < 0s 时 iL = 0 A , ∴ uL = 0V
=
uC
(1)
+
1 C
t 1

电路分析答案第五章

电路分析答案第五章

第五章 习题5、1 如题5、1图所示电路,时已处于稳态。

当时开关S 打开,求初始值与。

解:根据电容电压不能突变,有: S 打开时有: 可得:5、2 如题5、2图所示电路,解:时处于稳态,有: 根据电容电压、电感电流不能突变,当开关S(0)(0)4(0)(0)8148184L C C L u i u i V ++++=⨯+-⨯=⨯+-⨯=5、3 如题5、3图所示电路,时已处于稳态。

当时开关S 闭合,求与。

解:时, 有:5、4 如题5、4图所示电路,问开关打开时,电压表就是否会损坏？ 解:当开关闭合时,有:当开关打开时,有:所产生得电压为:可见超出了电压表得量程,因此电压表会损坏。

5、5 如题5、5图所示电路,时已处于稳态。

当时开关S 打开,求初始值与、。

解:开关闭合时, 电阻上得电压为:所以有根据电容电压不能突变,开关打开时可得:5、6 如题5、6图所示电路,时已处于稳态。

当时开关S 从1打到2,试求时电流,并画出其波形。

解:开关S 位于1时,有:开关S 位于2时,建立得方程:为等效电阻得电压 而 可得微分方程: 初始条件: 解方程: 特征根为则有: 代入初始条件可得: 得:根据分流关系,可得:5、7 如题5、7图所示电路,电感初始储能为零,当时开关S 闭合,试求时电流,并画出其波形。

解:已知 当开关闭合时,有:根据KVL 有: 整理可得: 方程得齐次解为: 方程得特解为: 代入方程有: 可得: 全解为: 代入初始条件,可得: 得:5、8 如题5、8图所示电路,电容初始储能为零,当时开关S 闭合,试求时得、与。

解:已知开关闭合时,将电路等效为简单得RC 串联, 以建立方程,有:代入参数有:方程齐次解为:方程得特解为: 代入方程可知 所以有: 代入初始条件可得: 得:5、9 如题5、9图所示电路,时已处于稳态。

当时开关S 闭合,求时电压与电流得零输入响应与零状态响应。

解:设C=0、1F,开关闭合时建立方程,有:两式整理可得: 电容初始电压为: 零输入响应方程为:解得形式为: 代入初始条件可得: 得:零状态响应方程为: 其齐次为:其特解为: 代入方程有: 可知: 通解为: 代入初始条件: 得:根据分流关系,可知电流得零输入响应为:再根据回路列KVL 方程: 整理可得:5、10 如题5、10图所示电路,时开关S 位于1,电路已处于稳态。

电路分析答案第五章

电路分析答案第五章

电路分析答案第五章第五章习题5.1 如题5.1图所⽰电路，0t <时已处于稳态。

当0t =时开关S 打开，求初始值(0)C u +和(0)C i +。

解：根据电容电压不能突变，有： 4(0)6424C u V -=?=+ S 打开时有： (0)(0)4C C u u V +-== 可得： 1(0)(0)0.814C C i u A ++=-?=-+5.2 如题5.2图所⽰电路，0t <时已处于稳态。

当0t =时开关S 闭合，求初始值(0)L u +、(0)C i +和(0)i +。

解：0t <时处于稳态，有： 12(0)148L i A -==+ (0)(0)88C L u i V --=?=根据电容电压、电感电流不能突变，当开关S12(0)12(0)(0)144C C C u u i A +-+--=== (0)(0)4(0)(0)8148184L C C L u i u i V ++++=?+-?=?+-?= (0)(0)(0)112C L i i i A +++=+=+=5.3 如题5.3图所⽰电路，0t <时已处于稳态。

当0t =时开关S 闭合，求(0)L i +和(0)Ldi dt+。

解：0t <时，A Vi L 144)0(=Ω=- 有： A i i L L 1)0()0(==-+5.4 如题5.4图所⽰电路，电压表的内阻10V R k =Ω，量程为100V 。

开关S 在0t =时打开，问开关打开时，电压表是否会损坏？解：当开关闭合时，有：24==6(0)4L L i A i -=当开关打开时，有：(0)(0)6L L i i A +-==所产⽣的电压为： (0)61060V L V u i R k kV +=?=?Ω=可见超出了电压表的量程，因此电压表会损坏。

5.5 如题5.5图所⽰电路，0t <时已处于稳态。

当0t =时开关S 打开，求初始值(0)C u +和1(0)L i +、2(0)L i +。

电路分析基础习题第五章答案(史健芳)

电路分析基础习题第五章答案(史健芳)

第5章5.1选择题1、在关联参考方向下，R 、L 、C 三个元件的伏安关系可分别如（ D ）表示。

A. dt di C u d i L u u Gu i C C tL L L R R =+==⎰ ,)(1)0( ,0ττ B. dtdi C u d i L u Ri u C C t L L R R =+==⎰ ,)(1 )0(u , 0L ττ C. ⎰+===tC C C L L R R d i C u u dt di L u Gi u 0)(1)0( , ,ττ D. ⎰+===tC C C L L R R d i C u u dt di L u Ri u 0)(1)0( , ,ττ 2、一阶电路的零输入响应是指（ D ）。

A. 电容电压V 0)0(≠-C u 或电感电压V 0)0(≠-L u , 且电路有外加激励作用B. 电容电流A 0)0(≠-C i 或电感电压V 0)0(≠-L u , 且电路无外加激励作用C. 电容电流A 0)0(≠-C i 或电感电压A 0)0(≠-L i , 且电路有外加激励作用D. 电容电压V 0)0(≠-C u 或电感电流A 0)0(≠-L i , 且电路无外加激励作用 3、若1C 、2C 两电容并联，则其等效电容C =（ A ）。

A. 21C C +B.2121C C C C +C.2121C C C C +D. 21C C4、已知电路如图x5.1 所示，电路原已稳定，开关闭合后电容电压的初始值)0(+C u 等 于（ A ）。

A. V 2-B. V 2C. V 6D. V 8图x5.1 选择题4图5、已知V 15)(τtC e t u -=，当s 2=t 时V 6=C u ，电路的时间常数τ等于（ B ）。

A. s 458.0B. s 18.2C. s 2.0D. s 1.06、二阶RLC 串联电路，当C L R 2____时，电路为欠阻尼情况；当CLR 2____时， 电路为临界阻尼情况（ B ）。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第5章选择题1、在关联参考方向下，R 、L 、C 三个元件的伏安关系可分别如（ D ）表示。

A. dtdi C u d i L u u Gu i C C tL L L R R =+==⎰ ,)(1)0( ,0ττ B. dtdi C u d i L u Ri u C C tL L R R =+==⎰ ,)(1 )0(u , 0L ττC. ⎰+===tC C C L L R R d i C u u dt di L u Gi u 0)(1)0( , ,ττ D. ⎰+===tC C C L L R R d i C u u dt di Lu Ri u 0)(1)0( , ,ττ 2、一阶电路的零输入响应是指（ D ）。

A. 电容电压V 0)0(≠-C u 或电感电压V 0)0(≠-L u , 且电路有外加激励作用B. 电容电流A 0)0(≠-C i 或电感电压V 0)0(≠-L u , 且电路无外加激励作用C. 电容电流A 0)0(≠-C i 或电感电压A 0)0(≠-L i , 且电路有外加激励作用D. 电容电压V 0)0(≠-C u 或电感电流A 0)0(≠-L i , 且电路无外加激励作用 3、若1C 、2C 两电容并联，则其等效电容C =（ A ）。

A. 21C C +B.2121C C C C +C.2121C C C C +D. 21C C4、已知电路如图 所示，电路原已稳定，开关闭合后电容电压的初始值)0(+C u 等 于（ A ）。

A. V 2-B. V 2C. V 6D. V 85、已知V 15)(τtC e t u -=，当s 2=t 时V 6=C u ，电路的时间常数τ等于（ B ）。

A. s 458.0B. s 18.2C. s 2.0D. s 1.06、二阶RLC 串联电路，当C L R 2____时，电路为欠阻尼情况；当CL R 2____时， 电路为临界阻尼情况（ B ）。

A. >、= B. <、=C. <、>D. >、<填空题1. 若L 1 、L 2两电感串联，则其等效电感L=；把这两个电感并联，则等效电Cu 21L L +2121L L L L +感L= 。

2. 一般情况下，电感的 电流 不能跃变，电容的 电压 不能跃变。

3. 在一阶RC 电路中，若C 不变，R 越大，则换路后过渡过程越 长 。

4. 二阶RLC 串联电路，当R < 2C L /时，电路为振荡放电；当R= 0 时，电路发生等幅振荡。

5. 如图示电路中，开关闭合前电路处于稳态，()+0u = -4 V ，+0d d t u C =2×104V/s 。

图 填空题5图6. R =1Ω和C =1F 的并联电路与电流源I S 接通。

若已知当I S =2A ()t ≥0，电容初始电压为1V 时，u t C ()为 t - ()t ≥0，则当激励I S 增大一倍（即I S A =4），而初始电压保持原值，t ≥0时u t C ()应为V )e 34(t --。

计算题1. 电路如图所示，（1）求图（a ）中ab 端的等效电容；（2）求图（b ）中ab 端的等效电感。

(a)(b)图 计算题1图解：(1)ab 两端的等效电容F C ab μ610)101011011()101011011(10=+++++⨯=（2）ab 两端的等效电感H L ab 1066)66(6)66(=+++⨯+=10F10F10F10F10F2. 电路图（a ）所示，电压源S u 波形如图（b ）所示。

（1）求电容电流，并画出波形图；（2）求电容的储能，并画出电容储能随时间变化的曲线。

解：由图可知所以电流波形图为⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤-⨯<≤-<≤+⨯-<≤<≤⨯=s t t s t s t t s t s t t t u C μμμμμ87 4010575 553 2010531 510 105)(666⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤<≤<≤-<≤<≤==s t A s t st A s t s t A dt t du c t i c C μμμμμ87 1075 053 1031 010 10)()(μs⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤⨯-<≤⨯<≤⨯-⨯<≤⨯<≤⨯==--s t s t st st s t s t s t t t C W u C C μμμμμμμ87 10 )8(2575 105.253 10)4(2531 105.210 1025)(21)t (625625622电容储能储能变化曲线为3．如图（a ）所示电路，A 00=）（L i ，电压源S u 的波形如图（b ）所示。

求当t =1s 、t =2s 、t =3s 、t =4s 时的电感电流i L 。

（a ） （b ）图 计算题3图解：电感电压与电流的关系为⎰+=tt d u Lt i t 0)(1)()(i 0ζζ各时段，电感电压的表达式为⎪⎩⎪⎨⎧>≥->≥≥≥=st s t s t s t s V V t u 34,401023,002,10)( 所以，t=1s 时，有 ⎰=-⨯==+=1015.2)]01(5.2[41010410)1(|V V t dt it=2s 时，有⎰=-⨯+=+=+=2115)]12(5.25.2[4105.210415.2)2(|V V t dt i t=3s 时，有⎰=+=3250415)3(V dt it=4s 时，有μsW C 5.2⨯V t t dt t i 75.344024105)4010(415)4(||4343432=-⨯+=-+=⎰4. 如图所示S 闭合瞬间（t=0），求初始值u C (0+),、i C (0+)。

解：t=0-时，s 断开，等效电路如图(a)。

V V V u i c c 1002080)0( ,0)0(=+==--图 计算题4图t=0+时，s 闭合，等效电路如图(b)。

V u c 100)0()0(u c ==-+A u i c c 210)0(80)0(-=-=++5. 如图所示电路的暂态过程中， 求i L 的初始值，稳态值以及电路的时间常 数τ各等于多少？如R 1增大，电路的时间 常数τ如何变化？解： 当t=0-时，s 断开， 等效电路如图如图(a) 电路中的电流恒定不变 A i L 5.22210)0(=+=-由换路定理：Ai i L L 5.2)0()0(==-+当t=0+时，s 闭合，等效电路如图如图(b), 电路稳定后 ， 在电路放电过程中时间常数 ，与R 1无关所以R 1增大，τ不变。

6. 如图已知：E=6V ，R 1=5Ω，R 2=4Ω， R 3=1Ω，开关S 闭合前电路处于稳态，t=0时 闭合开关S 。

求：换路瞬间的u L (0+)、i C (0+)。

解：当t=0-时，s 断开，电路处于稳态 等效电路如图(a)。

V i c 0)0(=-V R R R E u A R R E i L 1)0( ,1)0(313c 31=+⋅==+=--由换路定理：V u u A i i C C L L 1)0()0( ,1)0()0(====-+-+当t=0+时，s 闭合等效电路如图(a)。

A R u E i c c 25.1)0()0(2=-=++7. 如图所示电路，t=0时开关K 闭合， 求t 0时的u C (t)、i C (t)和i 3(t)。

已知： I S =5A ，R 1=10，R 2=10，R 3=5，C=250F ， 开关闭合前电路已处于稳态。

解：当t=0-时，k 断开，电路处于稳态，等效电路5.02==RL τA i L 0)(=+∞VR i E u L L 5)0()0(3=-=++如图(a)。

由换路定理：当t=0+时，k 闭合，t=+∞时，电路 达到新的稳态，等效电路如图(b)。

电容两端的等效电阻：时间常数：8. 如图所示电路中，t=0时试用三要素 法求出t ≥0时的i L (t)和u L (t)，并画出i L (t) 的波形。

（注：在开关动作前，电路已达稳态）。

解：当t=0-时，开关S1闭合，S2打开，电路 处于稳态，等效电路如图(a)。

得 A i L 10110)0(==- 由换路定理：当t=0+时，s1断开，s2闭合，AI i s 5)0(3==-VR i u c 25)0()0(33==--0)0(=-c i Vu u C C 25)0()0(==-+A I R R R R i S 2)(32113=++=+∞Vi R 10)()(u 33C =+∞=+∞Ω=+=4//)(321R R R R eq SC R eq 310-==τ[]V e e e u u u t ut t tC C C C 100010001510)1025(10)()0()()(---++=-+=+∞-++∞=τA i i L L 10)0()0(==-+达到新的稳态，等效电路如图（b ）。

根据图（c ）求等效电阻:)(t i L 的波形为9. 如图题所示电路在t <0已处于稳态，在t = 0时将开关S 由1切换至2，求： （1）换路后的电容电压）（t u C ； （2）t =20ms 时的电容元件的储能。

解：当t=0-时，开关S 在位置1，电路 处于稳态，等效电路如图(a)。

54V )0()0(V5490150010001500)0(===⨯+=-+-c c c u u u 则Ω=+⨯=12222eqR A i L 326)(==∞s R L eq 5.0==τt Le dt di L t u 27)(--=⋅=A e e i i i t i t t L L L L )73()]()0([)()(2--+=∞-++∞=τt=∞时等效电路如图(b)。

V 0)(=∞c ut=20ms 时：10．电路如图所示，电路原处 于稳态。

在t = 0时将开关S 由位置1合 向位置2，试求t ﹥0时i L （t ）和i （t ）， 并画出它们随时间变化的曲线。

解：t=0-时，电感相当于短路，等效电路如图(a)：t →∞时，电感所在支路短路。

等效电路如 图(b)：t V 54)0((t)s025.010505005001500//750025.06≥===⨯⨯==Ω==--+-t tc eq eq e e u u C R R ττW 0147.026.24105021)(21Wc(t)V26.245454(0.02)2628.0025.002.0=⨯⨯⨯======---t cu e eu cc A3.015303015//30109)0(=+⨯+=-L i A2.015303015//30106)(-=+⨯+-=∞L i A3.0)0()0(=-=+L L i i求等效电阻： 求时间常数：11. 在如图所示电路中，已知μF 1H 1V 10===C L U S ，，， 开关S 原来合在触点1处，在t =0 时，开关由触点1合到触点2处。