数字电路第4章(5加法器)_2

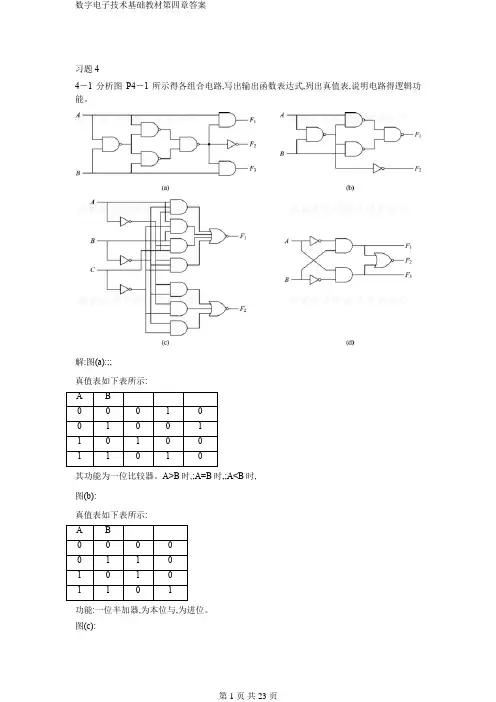
习题44－1 分析图P4－1所示得各组合电路,写出输出函数表达式,列出真值表,说明电路得逻辑功能。

解:图(a):;;真值表如下表所示:其功能为一位比较器。

A>B时,;A=B时,;A<B时,图(b):真值表如下表所示:功能:一位半加器,为本位与,为进位。

图(c):真值表如下表所示:功能:一位全加器,为本位与,为本位向高位得进位。

图(d):;;功能:为一位比较器,A<B时,＝1;A=B时,＝1;A>B时,＝14－2 分析图P4－2所示得组合电路,写出输出函数表达式,列出真值表,指出该电路完成得逻辑功能。

解:该电路得输出逻辑函数表达式为:因此该电路就是一个四选一数据选择器,其真值表如下表所示:,当M＝1时,完成4为二进制码至格雷码得转换;当M＝0时,完成4为格雷码至二进制得转换。

试分别写出,,,得逻辑函数得表达式,并列出真值表,说明该电路得工作原理。

解:该电路得输入为,输出为。

真值表如下:由此可得:完成二进制至格雷码得转换。

完成格雷码至二进制得转换。

4－4 图P4－4就是一个多功能逻辑运算电路,图中,,,为控制输入端。

试列表说明电路在,,,得各种取值组合下F与A,B得逻辑关系。

解:,功能如下表所示,两个变量有四个最小项,最多可构造种不同得组合,因此该电路就是一个能产生十六种函数得多功能逻辑运算器电路。

4－5 已知某组合电路得输出波形如图P4－5所示,试用最少得或非门实现之。

解:电路图如下:4－6 用逻辑门设计一个受光,声与触摸控制得电灯开关逻辑电路,分别用A,B,C表示光,声与触摸信号,用F表示电灯。

灯亮得条件就是:无论有无光,声信号,只要有人触摸开关,灯就亮;当无人触摸开关时,只有当无关,有声音时灯才亮。

试列出真值表,写出输出函数表达式,并画出最简逻辑电路图。

解:根据题意,列出真值表如下:由真值表可以作出卡诺图,如下图:C AB 00 10 11 100 1由卡诺图得到它得逻辑表达式为: 由此得到逻辑电路为:4－7 用逻辑门设计一个多输出逻辑电路,输入为8421BCD 码,输出为3个检测信号。

数电阎石第五版习题答案_第二章、第四章在学习数字电子技术这门课程时，阎石教授编写的第五版教材是许多同学的重要参考资料。

而其中的习题对于我们巩固知识、提升能力更是起到了关键作用。

接下来，让我们一起深入探讨第二章和第四章的习题答案。

第二章主要涉及逻辑代数基础。

逻辑代数是数字电路分析和设计的重要工具。

在这一章的习题中，我们首先要熟练掌握基本的逻辑运算，包括与、或、非、与非、或非、异或和同或等。

对于这些运算，我们需要清楚它们的真值表、逻辑表达式以及逻辑符号。

例如，有这样一道习题：已知逻辑函数 F ＝ A ＋ BC，求其反函数。

我们知道，求反函数的方法是将原函数中的与运算变为或运算，或运算变为与运算，0 变为 1，1 变为 0，同时原变量变为反变量，反变量变为原变量。

那么，F 的反函数 F' ＝（A' ·（B' ＋ C'））。

在处理逻辑函数的化简问题时，我们可以运用公式法、卡诺图法等多种方法。

公式法需要我们牢记各种逻辑代数的公式和定理，如摩根定律、吸收律等。

而卡诺图法则更加直观，通过将逻辑函数填入卡诺图，然后根据相邻最小项合并的原则进行化简。

再比如，给定一个复杂的逻辑函数 F ＝ AB ＋ A'C ＋ BC'，我们用卡诺图来化简。

先画出四变量的卡诺图，将函数中的各项对应填入，然后可以发现相邻的最小项可以合并，最终化简得到 F ＝ A ＋ C 。

在第二章的习题中，还会涉及到逻辑函数的表示方法及其相互转换。

逻辑函数可以用真值表、逻辑表达式、逻辑图、卡诺图等多种形式表示。

我们需要能够熟练地在这些表示方法之间进行转换。

例如，给出一个逻辑表达式 F ＝（A ＋ B)（C ＋ D) ，要画出其对应的逻辑图。

我们先将表达式展开得到 F ＝ AC ＋ AD ＋ BC ＋ BD ，然后根据每个与或项画出对应的逻辑门，最后连接起来就得到了逻辑图。

第四章则侧重于组合逻辑电路。

《数字电⼦技术基础》复习指导（第四章）第四章组合逻辑电路⼀、本章知识点(⼀)概念1.组合电路：电路在任⼀时刻输出仅取决于该时刻的输⼊，⽽与电路原来的状态⽆关。

电路结构特点：只有门电路，不含存储（记忆）单元。

2.编码器的逻辑功能：把输⼊的每⼀个⾼、低电平信号编成⼀个对应的⼆进制代码。

优先编码器：⼏个输⼊信号同时出现时，只对其中优先权最⾼的⼀个进⾏编码。

3.译码器的逻辑功能：输⼊⼆进制代码，输出⾼、低电平信号。

显⽰译码器：半导体数码管(LED数码管)、液晶显⽰器(LCD)4.数据选择器：从⼀组输⼊数据中选出某⼀个输出的电路，也称为多路开关。

5.加法器半加器：不考虑来⾃低位的进位的两个1位⼆进制数相加的电路。

全加器：带低位进位的两个 1 位⼆进制数相加的电路。

超前进位加法器与串⾏进位加法器相⽐虽然电路⽐较复杂，但其速度快。

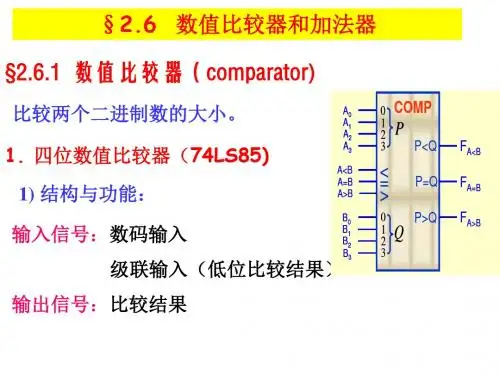
6.数值⽐较器：⽐较两个数字⼤⼩的各种逻辑电路。

7.组合逻辑电路中的竞争⼀冒险现象竞争：门电路两个输⼊信号同时向相反跳变(⼀个从1变0，另⼀个从0变1)的现象。

竞争-冒险：由于竞争⽽在电路输出端可能产⽣尖峰脉冲的现象。

消除竞争⼀冒险现象的⽅法：接⼊滤波电容、引⼊选通脉冲、修改逻辑设计(⼆)组合逻辑电路的分析⽅法分析步骤：1.由图写出逻辑函数式，并作适当化简；注意：写逻辑函数式时从输⼊到输出逐级写出。

2.由函数式列出真值表；3.根据真值表说明电路功能。

(三)组合逻辑电路的设计⽅法设计步骤：1.逻辑抽象：设计要求----⽂字描述的具有⼀定因果关系的事件。

逻辑要求---真值表(1) 设定变量--根据因果关系确定输⼊、输出变量；(2)状态赋值：定义逻辑状态的含意输⼊、输出变量的两种不同状态分别⽤0、1代表。

(3)列出真值表2.由真值表写出逻辑函数式真值表→函数式，有时可省略。

3.选定器件的类型可选⽤⼩规模门电路，中规模常⽤组合逻辑器件或可编程逻辑器件。

4.函数化简或变换式(1)⽤门电路进⾏设计：从真值表----卡诺图/公式法化简。

第4章全加器设计应用4.1全加器设计在计算机工程中，全加器是一种逻辑电路，用于将两个输入位和上一个进位位相加，并产生一个和位和一个进位位。

全加器是构成数字逻辑中任何计算机系统的基本构建模块之一一个全加器可以通过与门、或门和异或门组合构建。

它有三个输入（A、B和进位位C_in）和两个输出（和位S和进位位C_out）。

全加器的真值表如下所示：A B C_in S C_out0000000110010100110110010101011100111111全加器的电路图如下所示：_______________A_______，，____，，___AND1XOR1ORB_______，____，____，_________，_________，_____C_in ________，____4.2全加器的应用全加器是计算机系统中的关键组件，用于实现各种数学和逻辑运算。

下面是全加器的一些应用：1.加法器：全加器可以用来实现两个二进制数的加法运算。

将两个二进制数的每一位与对应的进位位输入到全加器中，从低位到高位依次相加，得到结果和位和进位位。

2.减法器：通过对减数取反，并在最低位的进位位上加上1，然后将减数和被减数与对应的进位位输入到全加器中，可以实现两个二进制数的减法运算。

3.乘法器：乘法器可以使用连续加法器来实现。

将两个二进制数的每一位与对应的进位位输入到全加器中，然后按照乘法运算规则依次相加，最终得到结果。

4.除法器：除法器可以使用连续减法器来实现。

将被除数和除数与对应的进位位输入到全加器中，然后按照除法运算规则依次相减，直到减数小于零为止，最终得到商和余数。

5.比较器：通过将两个二进制数的每一位与对应的进位位输入到全加器中，然后比较结果和进位位，可以判断两个二进制数的大小关系。

6.码转换器：全加器可以用来实现BCD码和8421码之间的转换。

BCD码是二进制编码和十进制数字之间的一种表示方法，而8421码是一种用来表示四位二进制数的编码。

加法器电路原理加法器电路是数字电子技术中常见的一种电路，它可以将多个输入信号相加，并输出它们的和。

在数字系统中，加法器电路是非常基础且重要的一部分，它广泛应用于计算机、通信系统、数字信号处理等领域。

本文将介绍加法器电路的原理及其实现方法。

加法器电路的原理基于二进制加法运算。

在二进制系统中，加法器电路可以将两个二进制数相加得到它们的和，并且可以处理进位的情况。

在实际的数字电路中，加法器电路通常由多个逻辑门组成，包括与门、或门、异或门等。

通过这些逻辑门的组合，可以实现不同位数的加法运算。

一般来说，加法器电路可以分为半加器和全加器两种。

半加器用于处理两个单独位的加法运算，它可以得到两个输入位的和以及进位输出。

而全加器则可以处理三个输入位的加法运算，包括两个输入位和一个来自上一位的进位，它可以得到三个输入位的和以及进位输出。

通过多个全加器的级联，可以实现多位数的加法运算。

在实际的电路设计中，加法器电路的实现方式多种多样。

最常见的是采用逻辑门的组合来实现加法器电路，例如使用异或门来实现不带进位的加法运算，再结合与门来处理进位的情况。

此外，还可以使用集成电路芯片或者可编程逻辑器件来实现加法器电路，这样可以提高电路的集成度和性能。

除了基本的加法器电路外，还可以通过增加控制信号或者引入特定的逻辑结构来实现更复杂的加法器电路。

例如，可以设计带有溢出检测功能的加法器电路，以便在加法运算溢出时给出相应的标志信号。

此外，还可以设计带有输入输出端口的加法器电路，以实现与其他模块的接口和数据交换。

总之，加法器电路是数字电子技术中非常重要的一部分，它可以实现数字系统中的加法运算，并且具有广泛的应用。

通过深入理解加法器电路的原理及其实现方法，可以更好地应用它们于实际的数字系统中，从而提高系统的性能和可靠性。

希望本文能够对读者对加法器电路有所帮助，并且能够在实际应用中发挥作用。

1 设计任务描述1.1设计题目：加法运算电路1.2 设计要求1.2.1 设计目的(1) 掌握1位十进制加法运算电路的构成，原理和设计原理；(2)熟悉集成电路的使用方法。

1.2.2 基本要求(1) 设计键盘以及编码电路；(2) 设计加数寄存器A和被加数寄存器B单元；(3) 实现4bit二进制码加法的BCD调整；(3) 用数码管以十进制形式显示最后运算结果。

1.2.3 发挥部分(1) 拓展十进制减法；(2) MR存储运算中间值；(3)其他。

2 设计思路根据此次课程设计的要求，我设计的简单计算器包括两大部分：加法计算部分，减法计算部分。

其中加法计算部分由五个部分组成，键盘及编码电路、加数寄存器A和被加数寄存器B、加法运算电路、4bit二进制码加法的BCD调整和译码显示器。

减法计算部分和加法计算部分共用同一个键盘，其他部分由反相器，求补逻辑电路以及相应的译码显示器组成。

其中有几个难点：如何实现2位十进制和怎样利用寄存器把数据传输到加法器中。

因为经键盘及编码器输出的是2进制数，那么寄存器接受并输出的数据也是2进制数，所以加法器输出的数据应是8421BCD码，使显示装置最终显示十进制数。

因为1位十进制数的8421BCD码与二进制数表现形式相同，但2位十进制数的8421BCD码与二进制数不同，所以我设计的加法运算装置是由两个74S283N芯片来实现2位十进制数的输出。

原理是让第二个芯片的一个输入端接第一个芯片的输出端，另一个输入端进行对第一个芯片的运算结果进行判断，大于等于10时输入6即2进制数的0110，反之输入0。

输出结果即为2位十进制数的8421BCD码。

寄存器的设计是由一个74LS374N芯片和两个74S194N芯片组成的，其中两个74S194N芯片并联后与74LS374N芯片串联。

74LS374N芯片的脉冲由键盘的数字键提供，使得按下数字键后该寄存器就存储输入的数字，并通过译码显示器显示。

两个74S194N芯片的脉冲分别由键盘的+号和=号提供，分别存储加数与被加数并输入到第一个74S283N芯片中运算。

数字电路加法器原理数字电路加法器是一种用于实现数字加法运算的电路。

它可以将两个二进制数相加，并输出其和。

在计算机和其他数字系统中，加法器是非常基础且重要的组件之一。

数字电路加法器的原理主要基于二进制加法的规则。

在二进制加法中，每一位的相加结果有四种可能：0+0=0，0+1=1，1+0=1，1+1=0（产生进位）。

这四种情况可以通过逻辑门来实现。

一个简单的加法器可以由多个半加器和一个全加器组成。

半加器用于计算两个输入位的和与进位，而全加器则用于计算包括上一位进位的三个输入位的和与进位。

通过级联多个半加器和全加器，可以构建出实现任意位数加法的加法器。

在加法器中，输入通常为两个二进制数和一个进位输入。

输出为两个二进制数相加的和和一个进位输出。

当两个输入数的每一位和进位输入都经过相应的逻辑运算后，得到了相应的输出结果。

在实际应用中，加法器常常是与其他数字电路组合使用的。

例如，在计算机的中央处理器中，加法器被用于实现整数加法、浮点数加法以及其他一些运算。

此外，加法器还可以用于实现其他数字运算，如减法、乘法和除法等。

除了基本的加法器，还有一些其他类型的加法器。

比如带有进位输入的全加器，可以通过输入一个外部进位信号来实现多位数的加法。

还有带有进位输出的全加器，可以将多个全加器级联，实现多位数相加时的进位传递。

在设计和实现加法器时，需要考虑到许多因素。

例如，加法器的延迟时间、功耗、面积等。

为了提高加法器的性能，可以使用一些优化技术，如并行加法器、流水线加法器和超前进位加法器等。

数字电路加法器是实现数字加法运算的基础组件。

它通过逻辑门的组合实现了二进制加法的规则，可以广泛应用于计算机和其他数字系统中。

加法器的设计和实现是数字电路设计中的重要内容，对于提高计算机的性能和效率具有重要意义。