正交变换的实例
- 格式:ppt
- 大小:3.21 MB
- 文档页数:109





正交变换法化二次型为标准型例题正交变换是线性代数中一个重要概念,它可以帮助我们将一个复杂的二次型化简为标准型,从而更好地理解和分析问题。
在本文中,我们将以正交变换法化二次型为标准型为主题,深入探讨其原理、方法和应用,并提供一个具体的例题来帮助读者更好地理解和掌握这一知识点。
1. 正交变换的概念和原理正交变换是指一个线性变换,在这个线性变换下,原来的向量空间中保持内积不变。
简单来说,就是变换后的向量之间的夹角保持不变。
在实际应用中,我们通常使用正交矩阵来进行正交变换,因为正交矩阵的行向量(或列向量)是两两正交彼此且模为1的向量。
2. 正交变换法化二次型为标准型的方法对于一个二次型矩阵A,我们可以通过正交变换将其化为标准型。
简单来说,就是存在一个正交矩阵P,使得P^TAP为对角矩阵。
这样做的好处在于,通过正交变换,我们可以将原来复杂的二次型化为易于分析和理解的标准型,从而更好地研究其性质和特点。
3. 一个具体的例题:将二次型矩阵化为标准型假设我们有一个二次型矩阵A,如下所示:A = [[3, 0, 0],[0, 2, -1],[0, -1, 2]]现在我们希望通过正交变换将其化为标准型。
我们可以按照以下步骤进行操作:(1)求出A的特征值和特征向量。
(2)将特征向量组成正交矩阵P。
(3)计算P^TAP,得到标准型矩阵。
通过具体的计算,我们可以得到最终的标准型矩阵B,如下所示:B = [[3, 0, 0],[0, 1, 0],[0, 0, 3]]4. 总结和回顾通过以上例题,我们深入探讨了正交变换法化二次型为标准型的方法,从而更好地理解了这一概念和原理。
通过正交变换,我们可以将原来复杂的二次型化为标准型,更好地研究其性质和特点。
这对于线性代数和数学分析领域的学习和研究具有重要意义。
5. 个人观点和理解我个人认为,正交变换法化二次型为标准型是线性代数中一个重要且实用的技巧。
通过正交变换,我们可以将复杂的二次型化简为简单的标准型,从而更好地理解和分析问题。

用正交变换将二次型化为标准型例题正交变换是线性代数中非常重要的概念,它能够将一个二次型矩阵化为标准型。
在本文中,我们将以一个具体的例题来说明如何使用正交变换将二次型化为标准型,帮助读者更深入地理解这一概念。
1. 例题描述假设有一个二次型矩阵Q如下:\[Q = \begin{bmatrix}2 & -1 & 0 \\-1 & 2 & 0 \\0 & 0 & 3 \\\end{bmatrix}\]我们的任务是使用正交变换将这个二次型矩阵化为标准型,并进行必要的计算和推导过程。
2. 步骤一:寻找正交矩阵我们需要寻找一个正交矩阵P,使得\[P^TQP = D\]其中D是一个对角矩阵,称为标准型矩阵。
3. 寻找特征值和特征向量我们先计算二次型矩阵Q的特征值和特征向量。
计算得到特征值为1,3,3,对应的特征向量分别为\[v_1 = \begin{bmatrix}1 \\-1 \\0 \\\end{bmatrix},v_2 = \begin{bmatrix}0 \\0 \\1 \\\end{bmatrix}\]4. 步骤二:构造正交矩阵接下来,我们可以使用特征向量构造正交矩阵P。
根据特征向量的定义,我们可以取单位化后的特征向量作为P的列向量,即\[P = \begin{bmatrix}\frac{1}{\sqrt{2}} & 0 \\-\frac{1}{\sqrt{2}} & 0 \\0 & 1 \\\end{bmatrix}\]5. 步骤三:进行正交变换现在,我们可以进行正交变换,计算\[P^TQP\]的结果。
将P带入计算,得到\[P^TQP = \begin{bmatrix}1 & 0 \\0 & 3 \\\end{bmatrix}\]6. 总结与回顾通过以上步骤,我们成功地使用正交变换将二次型矩阵Q化为标准型矩阵。
这说明正交变换在矩阵化简中的重要性和应用价值。




《正交变换的分类》一.概述正交变换是一种保持长度不变的线性变换(数域F中一个空间V 到自身的映射),在解析几何平面内保持这种关系或是等价关系或是全等关系。
其中包括平移、旋转、对折、或者是其中的组合等。
那么在欧氏空间(基本理论中有其概念)中,也会有如此的形式将一个向量经过某种途径将其变化而保持其长度不变。
在欧氏空间中实现这一变化和几何平面中几乎相同,它包括反射,旋转和这两种的组合,有限维数(两维以上)的空间中,这一变化可以实现,但是,实践起来并不容易。
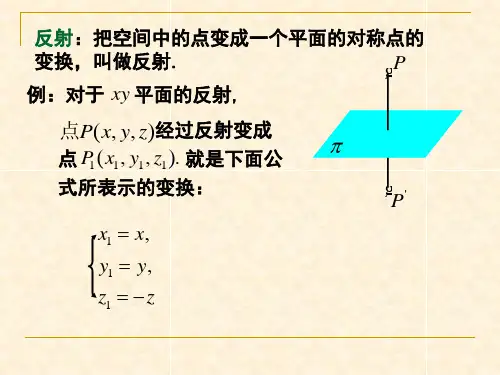
以一个简单例子引入,如图:αβ向量βα,在平面上采取了反射(或对称)变换使得βα=,这是平面中的实例。
那么在欧氏空间中,实现正交变换(反射,旋转还有而者的组合)会在论文中从二维和三维空间中步步引入。
二. 基础知识与理论基础 1. 正交变换的定义欧氏空间V 的一个线性变换叫δ作一个正交变换,如果对于任意V ∈ξ都有:|)(ξδ|=|ξ|2. 欧氏空间的概念设V 是实数域R 上一个向量空间。
如果对于V 中任意一对向量ηξ,有一个确定的记作<ηξ,>的实数与他们对应,叫作向量ξ与η的内积(或标量积),并且下列条件被满足:(i)<ηξ,>=<ξη,>(ii)<ζηξ,+>=<ζξ,>+<ζη,> (iii)<a ηξ,>=a<ηξ,> (iv)当0≠ξ时,<ξξ,>>0这里ζηξ,,是V 中任意向量,a 是任意实数,那么V 叫作这个内积来说的一个欧氏空间。
3. 正交矩阵n 维欧氏空间一个规范正交基到另外 一个规范正交基的过渡矩阵是一个正交矩阵。
有以下结论:UU T =U T U=I, U -1=U T4. 特征多项式定义设A=(a ij )是数域F 上一个n 阶矩阵。
行列式:f A (x)=det(XI-A)=1...312111an a a a x ----annx n a na n a ----................3...............2..............1.............. 叫作矩阵A 的特征矩阵多项式。
正交变换法化二次型为标准型例题一、引言正交变换法是线性代数中一个重要的概念,它在矩阵运算、特征值分解等领域都有广泛的应用。
在二次型化标准型的过程中,正交变换法起着至关重要的作用。
本文将通过一个具体的例题,深入探讨正交变换法化二次型为标准型的方法和过程,并结合个人的理解进行全面的解析。
二、例题及分析假设有一个二次型矩阵$A=\begin{bmatrix} 3&4\\4&-3\\\end{bmatrix}$,我们希望通过正交变换将其化为标准型。
1. 求解特征值和特征向量我们需要求解矩阵A的特征值和特征向量。
特征值可以通过解$|A-\lambda I|=0$得到,计算得到特征值为2和-2。
代入(A-2I)x=0和(A+2I)x=0中,可以求解得到相应的特征向量。
2. 构造正交矩阵接下来,我们需要构造正交矩阵T,使得$T^TAT$为对角矩阵。
由于A是一个2x2的矩阵,那么我们可以通过求解方程组$A=X\Lambda X^{-1}$得到正交矩阵X,其中Λ是特征值组成的对角矩阵。
3. 求解标准型通过正交变换$B=T^TAT$,我们可以得到矩阵B为标准型,即$B=\begin{bmatrix} 2&0\\0&-2\\ \end{bmatrix}$。
三、个人观点正交变换法是一种非常有用且强大的工具,它可以帮助我们简化矩阵的计算过程,同时也有助于更好地理解矩阵的性质。
通过对二次型的正交变换,我们可以将复杂的运算简化为一个更易于理解和操作的形式,这对于后续的研究和应用具有重要意义。
四、总结通过以上例题的深入分析,我们可以清晰地了解了正交变换法化二次型为标准型的具体步骤和方法。
在实际应用中,我们可以根据这一方法,将复杂的二次型矩阵化简为标准型,这不仅有助于简化计算,也有助于更深入地理解矩阵的性质和特点。
在学习和研究数学的过程中,正交变换法是一个重要且基础的概念,对于提高数学建模和问题求解的能力具有重要的意义。
第二章用正交变换化为标准型第一节2、1几种化标准形的方法2、1、1配方法2、1、2初等变换法2、1、3偏导数方法2、1、4雅可比方法第二节2、2用正交变换化为标准形2、2、1非退化线性替换的定义2、2、2正交替换法2、2、3例子2、2 用正交变换化为标准形2、2、1非退化线性替换的定义定义1、设x 1,…,x n ;y 1,…,y n 是两组文字,系数在数域P 中的一组关系式⎪⎪⎩⎪⎪⎨⎧+++=+++=+++=,..........,...22112222121212221111n nn n n nn n n n y c y c y c x y c y c y c x y c y c y c x 称为由x 1,…,x n 到y 1,…,y n 的一个线性替换,或简称线性替换,如果系数行列式ij c ≠0,那么线性替换就称为非退化的。
2、2、2正交替换法正交替换法:先写出二次型的矩阵A ,在用正交替换X=TY 将A 对角化,从而T ’AT=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡i 10λλ、、,其中λi(i=1,2,…,n)为二次型f(x 1,x 2,…x n )的矩阵的所有特征值,同时有f(x 1,x 2,…x n )=λ1y 21+λ2y 22+…+λny 2n2、2、3例子【例1】用正交变换化二次型f(x 1,x 2,x 3)=2x 21+5x 22+5x 23+4x 1x 2-4x 1x 3-8x 2x 3为标准形,要求写出所用的正交替换(广西师范大学*2001*(三)*15分)解:A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----542452222 A xE -=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----542452222x x x =x 3-12x 2+21x-10=(x-1)(x-1)(x-10)=0 x=1,1,10,(i) x=1E-A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----442442221--→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--000000221--→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-00000221η1=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-012 η2=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡102(ii) x=1010E-A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--542452228--→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-9945218180--→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-11452000--→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--00110102--→⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡0001102101 η3=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡--1121--→γ3⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---323231 γ1⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-05152 β2=η2-<η2,λ1> γ1=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡102+54⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-05152=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡102+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-05458=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡15452β2--→γ2=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡535534532令V=(γ1,γ2,γ3)=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---32535032534513153252 令X=UY 为所用正交变换,即Y=U ’Xf(x 1,x 2,x 3)=X ’AX=(UY)’AUY=Y ’U ’AUY=Y ’⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1011Y=y 21+y 22+10y 23为标准形【例2】用正交变换化二次型f(x 1,x 2,x 3)=x 21-2x 22+x 23+4x 1x 2+8x 1x 3+4x 2x 3为标准形,并写出所用的正交变换。
目录1引言 ................................................................................................................... 12正交变换的定义及其等价条件 ........................................................................ 12.1定义..................................................................................................................................12.2等价条件..........................................................................................................................23正交变换的应用................................................................................................ 43.1化二次型为标准形..........................................................................................................43.2解不变子空间相关问题..................................................................................................83.3求解矩阵问题..................................................................................................................83.4求解欧氏空间中其它相关问题......................................................................................83.5在积分中的应用.......................................................................................................... 114结束语 ............................................................................................................ 12参考文献 ........................................................................................................... 13致谢语 ............................................................................................................... 14正交变换的等价条件及其应用数学系2013级1班许鹏指导教师:陈金梅摘要:正交变换在大学学习中是一个重要的概念,例如在代数中,它涉及到了线性代数中一大部分的基本概念,如矩阵、向量、线性变换、标准正交基等,深入探讨研究这个课题对学好高等代数和线性代数十分有帮助.不仅如此,它在其他的领域也有着大范围的普及,如在积分的应用中,在多重积分的方面。