判别分析案例
- 格式:ppt
- 大小:3.35 MB
- 文档页数:43
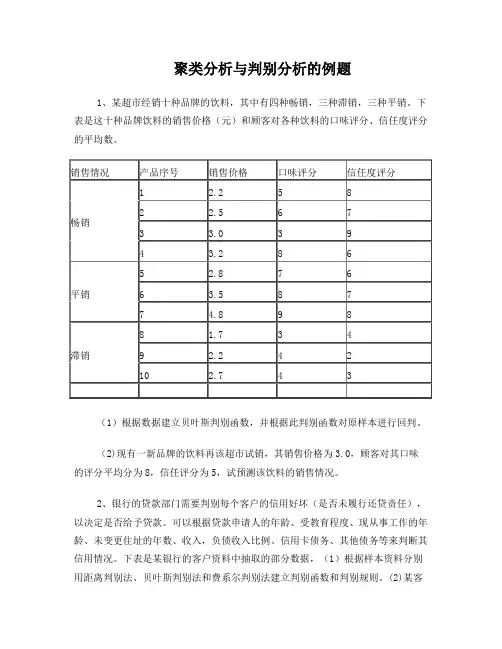
聚类分析与判别分析的例题1、某超市经销十种品牌的饮料,其中有四种畅销,三种滞销,三种平销。
下表是这十种品牌饮料的销售价格(元)和顾客对各种饮料的口味评分、信任度评分的平均数。
(1)根据数据建立贝叶斯判别函数,并根据此判别函数对原样本进行回判。
(2)现有一新品牌的饮料再该超市试销,其销售价格为3.0,顾客对其口味的评分平均分为8,信任评分为5,试预测该饮料的销售情况。
2、银行的贷款部门需要判别每个客户的信用好坏(是否未履行还贷责任),以决定是否给予贷款。
可以根据贷款申请人的年龄、受教育程度、现从事工作的年龄、未变更住址的年数、收入,负债收入比例、信用卡债务、其他债务等来判断其信用情况。
下表是某银行的客户资料中抽取的部分数据,(1)根据样本资料分别用距离判别法、贝叶斯判别法和费系尔判别法建立判别函数和判别规则。
(2)某客户的如上情况资料为(53,1,9,18,50,11,20,2.02,3.58),对其进行信用好坏的判别。
目前信用好坏客户序号已履行还贷责任1 23 1 7 2 31 6.6 0.34 1.712 34 1 173 59 8.0 1.81 2.913 42 2 7 23 41 4.6 0.94 0.944 39 1 195 48 13.1 1.93 4.365 35 1 9 1 34 5.0 0.40 1.30未履行还贷责任6 37 1 1 3 24 15.1 1.80 1.827 29 1 13 1 42 7.4 1.46 1.658 32 2 11 6 75 23.3 7.76 9.729 28 2 2 3 23 6.4 0.19 1.2910 26 1 4 3 27 10.5 2.47 0.363、从胃癌患者、萎缩性胃炎患者和非胃炎患者中分别抽取五个病人进行思想生化指标的化验:血清铜蛋白、蓝色反应、尿吲哚乙酸和中性硫化物,数据见下表。
试用距离判别法建立判别函数,并根据此判别函数对原样本进行回判。

例:研究某年全国各地区农民家庭收支的分布规律,根据抽样调查资料进行分类,共抽取28个省、市、自治区的六个指标数据。
先采用聚类分析,将28个省、市、自治区分为三组。
北京、上海、广州3个城市属于待判样本。
(家庭收支.sav)1.选中判别分析,2.选择Fisher 即bayes判别分析方法,易混!!!3.确定组别4. 选择保存结果5. 模型检验(即判别准确率)重要结果分类函数系数类别1 2 3食品.480 .473 .429 衣着 1.612 1.354 .933 燃料 2.421 2.189 .777 住房.555 .335 .052 用品及其它 1.032 .580 .847 文化支出 5.387 5.446 4.317(常量) -117.620 -89.052 -53.616Fisher 的线性判别式函数按照案例顺序的统计量案例数目实际组最高组第二最高组判别式得分预测组P(D>d |G=g)P(G=g| D=d)到质心的平方Mahalanobis距离组P(G=g| D=d)到质心的平方Mahalanobis距离函数1函数2 p df初始 1 1 1 .320 2 1.000 2.282 2 .000 22.754 3.163 -2.7172 1 1 .799 2 1.000 .449 2 .000 17.611 3.559 -1.6593 1 2**.095 2 .688 4.705 1 .312 6.283 2.737 1.2754 1 1 .797 2 .984 .453 2 .016 8.670 2.855 -.5695 1 1 .504 2 1.000 1.372 2 .000 20.770 4.205 -1.4616 1 1 .313 2 .996 2.321 2 .004 13.305 1.847 -2.1317 2 2 .788 2 .986 .476 1 .011 9.482 .566 .5958 2 2 .405 2 .992 1.806 1 .008 11.456 1.756 1.9139 2 2 .532 2 .987 1.263 1 .013 9.942 1.645 1.60710 2 2 .451 2 .999 1.593 1 .001 15.008 1.358 2.26911 2 2 .826 2 .984 .383 1 .015 8.758 .816 .71812 2 2 .769 2 .994 .524 1 .006 10.742 1.252 1.52313 2 2 .378 2 .861 1.945 3 .139 5.594 -.611 .53914 2 2 .219 2 .639 3.034 3 .361 4.179 -1.036 .60515 2 2 .304 2 .941 2.379 3 .059 7.903 -.943 1.59616 2 2 .935 2 .997 .134 1 .003 12.046 .874 1.48517 3 3 .387 2 .994 1.899 2 .006 12.039 -1.570 -1.44818 3 3 .801 2 1.000 .443 2 .000 19.449 -3.157 -1.07619 3 3 .413 2 .991 1.767 2 .009 11.104 -1.531 -1.30320 3 3 .570 2 .984 1.124 2 .016 9.398 -1.635 -.84721 3 3 .880 2 .997 .255 2 .003 11.791 -2.562 -.12822 3 3 .826 2 .993 .383 2 .007 10.155 -2.282 -.14023 3 3 .130 2 1.000 4.077 2 .000 29.305 -4.643 -.18324 3 3 .078 2 .995 5.095 2 .005 15.558 -3.369 1.52625 3 3 .323 2 1.000 2.260 2 .000 25.638 -3.294 -1.98926 未分组的1 .0002 1.000 20.223 2 .000 62.899 7.054 -3.27827 未分组的1 .0002 1.000 82.160 2 .000 150.236 11.796 -3.63028 未分组的1 .0052 1.000 10.431 2 .000 25.808 5.621 .759交叉验证a 1 1 1 .349 6 1.000 6.707 2 .000 27.3012 1 1 .025 6 .999 14.400 2 .001 29.4123 1 2**.087 6 1.000 11.051 1 .000 37.7404 1 1 .233 6 .900 8.064 2 .100 12.4595 1 1 .136 6 1.000 9.738 2 .000 28.7186 1 1 .182 6 .975 8.851 2 .025 16.1797 2 2 .249 6 .945 7.850 1 .043 14.0428 2 2 .734 6 .984 3.575 1 .016 11.8079 2 2 .039 6 .880 13.285 1 .120 17.26810 2 2 .078 6 .996 11.349 1 .004 22.46511 2 2 .701 6 .967 3.819 1 .031 10.68312 2 2 .461 6 .984 5.669 1 .016 13.90313 2 3**.129 6 .703 9.898 2 .297 11.62214 2 3**.444 6 .684 5.820 2 .316 7.36815 2 2 .123 6 .635 10.047 3 .365 11.15116 2 2 .000 6 .878 35.006 1 .121 38.97317 3 3 .114 6 .955 10.252 2 .044 16.40718 3 3 .925 6 1.000 1.939 2 .000 20.37119 3 3 .288 6 .959 7.373 2 .041 13.67820 3 3 .652 6 .963 4.186 2 .037 10.70721 3 3 .526 6 .991 5.139 2 .009 14.63422 3 3 .834 6 .986 2.792 2 .014 11.30223 3 3 .101 6 1.000 10.616 2 .000 39.41124 3 3 .018 6 .917 15.261 2 .083 20.05725 3 3 .268 6 1.000 7.611 2 .000 32.555对初始数据来说,平方Mahalanobis 距离基于典则函数。

例1. 现有分别来自总体A 和总体B 的两组随机样本,样本量分别为5和6,样本均值分别为⎪⎪⎭⎫⎝⎛00和⎪⎪⎭⎫⎝⎛23,样本离差阵分别为⎪⎪⎭⎫⎝⎛4004和⎪⎪⎭⎫ ⎝⎛5005.2。
今欲判别一个新样本⎪⎪⎭⎫⎝⎛2.11来自哪一个总体:(1). 请使用距离判别法(采用马氏距离)对上述新样本进行判别(不假设两个总体有相同的自协方差阵)。
(2). 请采用Fisher 判别法求出判别函数,并利用此判别函数对上述新样本进行判别。
解答:(1)、先求取新样本到不同总体均值的马氏距离: 44.22.11002.114004151002.112212=+=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-'⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫⎝⎛=-AMD64.88.022232.115005.2161232.112212=+⨯=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-'⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫⎝⎛=-B MD显然有22B AMD MD<,故此,应判别新样本来自总体A 。
(2) 、先求取线性判别函数: ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛=-+=--9/213/600235005.24004)()(11)2()1(A BX XSSu线性判别函数为:X X u y u '⎪⎪⎭⎫⎝⎛='=9/213/6)(。
新样本的判别函数值:7282.02.119/213/6)()0(≈⎪⎪⎭⎫⎝⎛'⎪⎪⎭⎫ ⎝⎛=X u ; 总体A 的均值的判别函数值:0)(=A X u ;总体B 的均值的判别函数值:829.1239/213/6)(≈⎪⎪⎭⎫⎝⎛'⎪⎪⎭⎫⎝⎛=B X u ; 临界值:9977.00116829.1)()(≈+⨯=+++BA B B BA A A n n n X u n n n X u ;由于)()(B A X u X u <,且7282.0)()0(≈X u 小于临界值0.9977,所以应判别新样本来自总体A 。


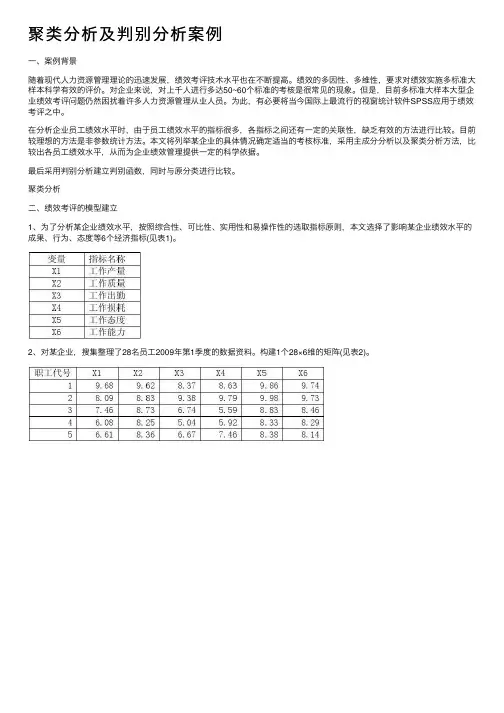
聚类分析及判别分析案例⼀、案例背景随着现代⼈⼒资源管理理论的迅速发展,绩效考评技术⽔平也在不断提⾼。
绩效的多因性、多维性,要求对绩效实施多标准⼤样本科学有效的评价。
对企业来说,对上千⼈进⾏多达50~60个标准的考核是很常见的现象。
但是,⽬前多标准⼤样本⼤型企业绩效考评问题仍然困扰着许多⼈⼒资源管理从业⼈员。
为此,有必要将当今国际上最流⾏的视窗统计软件SPSS应⽤于绩效考评之中。
在分析企业员⼯绩效⽔平时,由于员⼯绩效⽔平的指标很多,各指标之间还有⼀定的关联性,缺乏有效的⽅法进⾏⽐较。
⽬前较理想的⽅法是⾮参数统计⽅法。
本⽂将列举某企业的具体情况确定适当的考核标准,采⽤主成分分析以及聚类分析⽅法,⽐较出各员⼯绩效⽔平,从⽽为企业绩效管理提供⼀定的科学依据。
最后采⽤判别分析建⽴判别函数,同时与原分类进⾏⽐较。
聚类分析⼆、绩效考评的模型建⽴1、为了分析某企业绩效⽔平,按照综合性、可⽐性、实⽤性和易操作性的选取指标原则,本⽂选择了影响某企业绩效⽔平的成果、⾏为、态度等6个经济指标(见表1)。
2、对某企业,搜集整理了28名员⼯2009年第1季度的数据资料。
构建1个28×6维的矩阵(见表2)。
3、应⽤SPSS数据统计分析系统⾸先对变量进⾏及主成分分析,找到样本的主成分及各变量在成分中的得分。
去结果中的表3、表4、表5备⽤。
表 5成份得分系数矩阵a成份1 2Zscore(X1) .227 -.295Zscore(X2) .228 -.221Zscore(X3) .224 -.297Zscore(X4) .177 -.173Zscore(X5) .186 .572Zscore(X6) .185 .587提取⽅法 :主成份。
构成得分。
a. 系数已被标准化。
4、从表3中可得到前两个成分的特征值⼤于1,分别为3.944和1.08,所以选取两个主成分。
根据累计贡献率超过80%的⼀般选取原则,主成分1和主成分2的累计贡献率已达到了83.74%的⽔平,表明原来6个变量反映的信息可由两个主成分反映83.74%。

Wilks 的 Lambda卡方df Sig.函数检验Wilks 的Lambda1 到2 .025 538.950 8 .0002 .774 37.3513 .000标准化的典型判别式函数系数函数1 2花萼长-.346 .039花萼宽-.525 .742花瓣长.846 -.386花瓣宽.613 .555-=0.613⨯⨯0.846-1+3460.525.0花萼长z花萼宽花瓣长⨯z花瓣宽zD⨯+z=0.555⨯+0.3860.742⨯20.039-⨯花萼宽花瓣长花瓣宽花萼长zzD⨯+zz结构矩阵函数1 2花瓣长.726*.165花萼宽-.121 .879*花瓣宽.651 .718*花萼长.221 .340*判别变量和标准化典型判别式函数之间的汇聚组间相关性按函数内相关性的绝对大小排序的变量。
*. 每个变量和任意判别式函数间最大的绝对相关性0.1550.196--=0.299.0花瓣宽.2526-0631zz花萼长z花萼宽⨯z花瓣长⨯D⨯+⨯+0.089-+-=0.271 978⨯2.60.0070.218z花萼长z花萼宽花瓣长花瓣宽zz⨯⨯+D⨯+区域图典则判别函数 2-16.0 -12.0 -8.0 -4.0 .0 4.0 8.0 12.0 16.0+---------+---------+---------+---------+---------+---------+---------+---------+16.0 + 13 +I 13 II 13 II 123 II 123 II 12 23 I12.0 + + + + 12 23 + + + +I 12 23 II 12 23 II 12 23 II 12 23 II 12 23 I8.0 + + + + 12 + 23 + + + +I 12 23 II 12 23 II 12 23 II 12 23 II 12 23 I4.0 + + + + 12 + 23 + + + +I 12 23 II 12 23 II 12 23 II 12 23 II 12 23 * I.0 + + + * + 12 + 23 + + +I 12 * 23 II 12 23 II 12 23 II 12 23 II 12 23 I-4.0 + + + + 12 + + 23 + + +I 12 23 II 12 23 II 12 23 II 12 23 II 12 23 I-8.0 + + + +12 + + 23 + + +I 12 23 II 12 23 II 12 23 II 12 23 II 12 23 I-12.0 + + + 12 + + 23 + +I 12 23 II 12 23 II 12 23 II 12 23 II 12 23 I-16.0 + 12 23 ++---------+---------+---------+---------+---------+---------+---------+---------+ -16.0 -12.0 -8.0 -4.0 .0 4.0 8.0 12.0 16.0典则判别函数 1区域图中使用的符号符号组标签---- -- --------------1 1 刚毛鸢尾花2 2 变色鸢尾花3 3 佛吉尼亚鸢尾花* 表示一个组质心。
实验、判别分析
一、实验名称:判别分析
二、实验目的:通过本实验掌握使用SPSS进行判别分析
三、实验过程:
1.判断解释变量是属性变量而解释变量是度量变量。
2.判断各组的变量得协方差矩阵相等,并用很简单的公式来计算判别函数和进行显著性检验。
3. 各判别变量间具有多元正态分布,精确计算显著性检验值和分组归属的概率。
四、分析结果:
特征值
函数特征值方差的 % 累积 % 正则相关性
1 18.207a91.6 91.6 .974
2 1.460a7.
3 98.9 .770
3 .212a 1.1 100.0 .419
a. 分析中使用了前 3 个典型判别式函数。
从表显示出典型分析最终形成三个判别函数,判别函数F1的特征值为18.207,判别函数F2的特征值为1.460,判别函数F3的特征值为0.212.可见判别函数F1的判别能力大于F2和F3。
该表是非标准化的典型判别函数系数,写成函数为:
对原始数据中未进行分类的职工进行典型的判别分析。
得到结果如上图,可知职工号为26、27、28三个职工分别被判入了第三类和第四类。
数据:
表示工作产量,表示工作质量,表示工作出勤
表示工作损耗,表示工作态度,表示工作能力
五、心得体会:
通过判别,我们知道了当遇到需要识别一个个体所属类别的情况时,就能够运用自己所学的判别分析的知识,去解决这一类的问题,并能够准确的将其分类,甚至在遇到多重共线性问题,也能使用判别分析来解决。
通过此次的报告过程,我们对判别分析有了更进一步得认识,受益颇多。


判别分析假设有k 个总体,判别分析就是根据某个个体的观察值来推断该个体是来自这k 个总体中哪一个总体。
下面的例子说明判别分析有着广泛的应用。
(1)根据已有的气象资料,如气温、气压等判断明天是晴天还是阴天,是有雨还是无雨。
明天的天气情况是未来的行为。
因为是未来行为,难以得到它的完全信息。
已有的气象资料仅是它的一部分信息。
基于未来行为的不完全信息对未来行为进行预测是判别分析的一个应用。
(2)在非洲发现了一种头盖骨化石,考古学家要研究它究竟是像猿(如黑猩猩)还是像人。
倘若研究对象是活的,就能对他进行各方面的观察,有充足乃至完全的信息。
但研究对象早就死了,他的很多重要信息都丢失了。
考古学家只能根据不完全信息,如牙齿的长宽来进行判断。
当信息丢失后,对过去的行为进行判断是判别分析的另一个应用。
(3)有时人们难以得到完全的信息,这里有两种情况。
情况之一是信息完全只能来自破坏性试验。
例如,汽车的寿命只有在把它用坏之后才知道。
一般地,希望根据一些测量指标(如零部件的性能)就能事先对汽车的寿命作出判断。
情况之二是获得完全信息的代价太高。
例如,有些疾病可用代价昂贵的检查或通过手术得到确诊。
但人们往往更希望用便于观察得到的一些外部症状来诊断体内的疾病,以避免过大的开支和损失。
在完全信息难以得到时,对行为判断是判别分析的又一格应用。
正因为判别分析是基于不完全信息作出的判断,它就不可避免地会犯错误,一个好的判别法则错判的概率应很小。
除了错判概率,在判别分析问题中还应考虑费用,一个好的判别法则错误的损失应很小。
关于判别法则优良性的讨论从略。
判别分析问题的描述:设有k 个m 维总体k G G G ,,,21 ,其分布特征已知(如已知分布函数分别为)(,),(),(21x F x F x F k ,或知道来自各个总体的训练样本)。
对给定的一个新样品X ,我们要判断它来自哪个总体。
在进行判别归类时,由假设的前提,判别的依据及处理的手法不同,可得出不同判别方法。
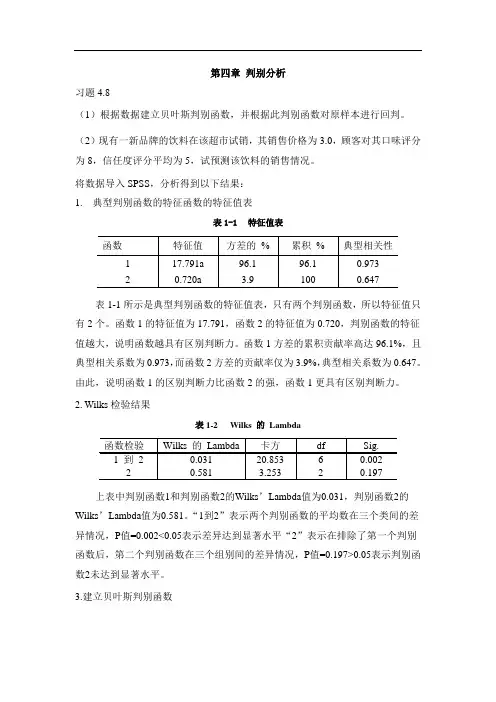
第四章判别分析习题4.8(1)根据数据建立贝叶斯判别函数,并根据此判别函数对原样本进行回判。
(2)现有一新品牌的饮料在该超市试销,其销售价格为3.0,顾客对其口味评分为8,信任度评分平均为5,试预测该饮料的销售情况。
将数据导入SPSS,分析得到以下结果:1.典型判别函数的特征函数的特征值表表1-1 特征值表表1-1所示是典型判别函数的特征值表,只有两个判别函数,所以特征值只有2个。
函数1的特征值为17.791,函数2的特征值为0.720,判别函数的特征值越大,说明函数越具有区别判断力。
函数1方差的累积贡献率高达96.1%,且典型相关系数为0.973,而函数2方差的贡献率仅为3.9%,典型相关系数为0.647。
由此,说明函数1的区别判断力比函数2的强,函数1更具有区别判断力。
2.Wilks检验结果表1-2 Wilks 的Lambda上表中判别函数1和判别函数2的Wilks’Lambda值为0.031,判别函数2的Wilks’Lambda值为0.581。
“1到2”表示两个判别函数的平均数在三个类间的差异情况,P值=0.002<0.05表示差异达到显著水平“2”表示在排除了第一个判别函数后,第二个判别函数在三个组别间的差异情况,P值=0.197>0.05表示判别函数2未达到显著水平。
3.建立贝叶斯判别函数表1-3 贝叶斯判别法函数系数上表为贝叶斯判别函数的系数矩阵,用数学表达式表示各类的贝叶斯判别函数为:第一组:F1=-81.843-11.689X1+12.97X2+16.761X3第二组:F2=-94.536-10.707X1+13.361X2+17.086X3第三组:F3=-17.499-2.194X1+4.960X2+6.447X3将新品牌饮料样品的自变量值分别代入上述三个贝叶斯判别函数,得到三个函数值为:F1=65.271,F2=65.661,F3=47.884比较三个值,可以看出F2=65.661最大,据此得出新品牌饮料样品应该属于第二组,即该饮料的销售情况为平销。
判别分析(一)SPSS11.5系统中判别分析选项卡内容介绍点击Data View窗口上方的Analyze按钮,出现菜单,然后把光标移至Classify 处,会出现下一级菜单,如图5.1所示,点击该菜单中的Discriminant(判别)栏目,便会出现Discriminant Analysis(判别分析)的选项卡,如图5.9所示,该卡上的内容有八个部分:(图5.9)Grouping Variable(组变量):指定分组变量及组变量值的范围。
首先把分组变量从左边的变量框内导入Grouping Variable矩形框中,然后点击Define Range按钮,在出现的对话框中输入组变量的最大值和最小值。
Independents(自变量):安排判别分析中的自变量。
·Enter independents togethe r:选定的自变量全部进入判别函数中,此是系统默认的项;·Use stepwise method:逐步进入,当点选该项时,Method(方法)被激活,单击Method按钮,出现如图5.10所示的对话框,通过该对话框可以设置逐步进入的方法。
Stepwise Method(逐步进入方法)对话框有三个部分:○1Method:设置逐步进入的方法,系统给出5个选项供选择,系统默认的选项是Wilks’ lambda(Wilks’ lambdaΛ值法):每步计算Wilks’ lambdaΛ值,该值最小的自变量进入判别函数。
○2Criteria:定义自变量进入判别函数或从判别函数中剔除的方法,系统给出两种方法:Use F value(用方差分析的F值),此为系统默认的项,但Entry(进入)和Removal(剔除)的值可以变动;Use probability of F(用方差分析的显著性水平),Entry和Removal(剔除)的值可以变动。
(图5.10)○3Display:设置输出内容,系统给出两个复选项:Summary of steps(输出变量进入判别函数的每一步),此为系统默认的选项;F for pairwise distances(输出各个变量不同水平的方差差异性检验)。
判别分析--线性判别分析(LDA)应⽤案例1 线性判别分析执⾏线性判别分析可使⽤lda()函数,且该函数有三种执⾏形式,依次尝试使⽤。
(1)公式formula格式我们使⽤nmkat变量作为待判别变量,其他剩余的变量作为特征变量,根据公式nmkat~使⽤训练集数据来运⾏lda()函数:library(MASS)library("MASS")fitlda1<-lda(nmkat~.,datatrain) #以公式格式执⾏判别分析names(fitlda1) #查看lda输出项名称结果分析:我们看到,可以根据lda()函数得到10项输出结果,分别为执⾏过程中所使⽤的先验概率prior、数据集中各类别的样本量counts、各变量在每⼀类别中的均值 means等。
fitlda1$prior #查看本次执⾏过程中所使⽤的先验概率fitlda1$counts #查看数据集datatrain中各类别的样本量结果分析:由于我们在之前的抽样过程中采⽤的是nmkat各等级的等概率分层抽样⽅式,因此如上各类别的先验概率和样本量在5个等级中都是相等的。
具体的,5类的先验概率都为0.2,之和为1,且训练集中每⼀类都抽出了144个样本。
fitlda1$means结果分析:在如上的均值输出结果中,我们可以看到⼀些很能反映现实情况的数据特征。
⽐如,对于占地⾯积wfl变量,它明显随着租⾦nmkat的升⾼⽽逐步提⾼,我们看到在租⾦为等级1(少于500马克)时,占地⾯积的均值仅为55.53平⽅⽶,⽽对于租⾦等级5(租⾦不低于1150 马克),平均占地⾯积则达到了92.24平⽅⽶。
⾯积越⼤的房屋租⾦越贵,这是⼗分符合常识的。
执⾏fitlda1可直接将判别结果输出。
(2)数据框data.frame及矩阵matrix格式由于这两种函数格式的主体参数都为x与grouping,我们放在⼀起实现,程序代码如下:fitlda2<-lda(datatrain[,-12],datatrain[,12])#设置属性变量(除第12个变量nmkat外)与待判别变量(第12个变量nmkat)的取值fitlda22.判别规则可视化我们⾸先使⽤plot()直接以判别规则fit_ldal为对象输出图形,如下图所⽰:plot(fitlda1)结果分析:从图可以看到,在所有4个线性判别式(Linear Discriminants,即 LD)下1⾄5这5个类别的分布情况,不同类别样本已⽤相应数字标出。
可编辑修改精选全文完整版实验报告5判别分析(设计性实验)(Discriminant analysis)实验原理:判别分析是判别样品所属类型的一种统计方法。
判别分析是在已知研究对象分成若干类型(或组别)并已取得各种类型的一批已知样品的观测数目,在此基础上根据某些准则建立判别式,然后对未知类型的样品进行判别分类。
本实验要求学生应用距离判别准则(即,对任给的一次观测,若它与第i类的重心距离最近,就认为它来自第i类),对两总体和多总体情形下分别进行判别分析。
实验中需注意协方差矩阵相等时,选取线性判别函数;协方差矩阵不相等时,应选取二次判别函数。
实验题目一:为了检测潜在的血友病A携带者,下表中给出了两组数据:(t11a8)其中x1=log10(AHF activity),x2=log10(AHF antigen)。
下表给出了五个新的观测,试对这些观测判别归类;(t11b8)实验要求:(1)分别检验两组数据是否大致满足二元正态性;(2)分别计算两组数据的协方差矩阵,是否可以认为两者近似相等?(3)对训练样本和新观测合并作散点图,不同的类用不同颜色标识;(4)用lda函数做判别分析,即在协方差矩阵相等的情形下作判别分析;(5)用qda函数做判别分析,即在协方差矩阵不相等的情形下作判别分析;(6)比较方法(4)和方法(5)的误判率。
实验题目二:某商学研究生院的招生官员利用指标――大学期间平均成绩GPA和研究生管理能力考试GMAT的成绩,将申请者分为三类:接受,不接受,待定。
下表中给出了三类申请者的GPA与GMAT成绩:(t11a6)GPA (x1)GMAT(x2)接受GPA(x1)GMAT(x2)不接受GPA(x1)GMAT(x2)待定2.96 596 1 2.54 446 2 2.86 494 33.14 473 1 2.43 425 2 2.85 496 3 3.22 482 1 2.2 474 2 3.14 419 3 3.29 527 1 2.36 531 2 3.28 371 3 3.69 505 1 2.57 542 2 2.89 447 3 3.46 693 1 2.35 406 2 3.15 313 3 3.03 626 1 2.51 412 2 3.5 402 3 3.19 663 1 2.51 458 2 2.89 485 3 3.63 447 1 2.36 399 2 2.8 444 33.59 588 1 2.36 482 2 3.13 416 33.3 563 1 2.66 420 2 3.01 471 33.4 553 1 2.68 414 2 2.79 490 33.5 572 1 2.48 533 2 2.89 431 33.78 591 1 2.46 509 2 2.91 446 33.44 692 1 2.63 504 2 2.75 546 33.48 528 1 2.44 336 2 2.73 467 33.47 552 1 2.13 408 2 3.12 463 33.35 520 1 2.41 469 2 3.08 440 33.39 543 1 2.55 538 2 3.03 419 33.28 523 1 2.31 505 2 3 509 33.21 530 1 2.41 489 2 3.03 438 33.58 564 1 2.19 411 2 3.05 399 33.33 565 1 2.35 321 2 2.85 483 33.4 431 1 2.6 394 2 3.01 453 33.38 605 1 2.55 528 2 3.03 414 33.26 664 1 2.72 399 2 3.04 446 33.6 609 1 2.85 381 23.37 559 1 2.9 384 23.8 521 13.76 646 13.24 467 1实验要求:(1)对上表中的数据作散点图,不同的类用不同的颜色标识;(2)用lda函数做判别分析,即在协方差矩阵相等的情形下作判别分析;(3)用qda函数做判别分析,即在协方差矩阵不相等的情形下作判别分析;(4)比较方法(2)和方法(3)的误判率;(5)现有一新申请者的GPA为3.21,GMAT成绩为497。