串联超前校正的计算方法
- 格式:doc
- 大小:496.04 KB
- 文档页数:6



6-4 串联迟后-超前校正一、迟后-超前校正网络串联迟后-超前校正,可以通过单独的迟后网络和超前网络来实现,如图6-12(a )。
也可以通过相位迟后-超前网络来实现,如图6-12(b )所示。
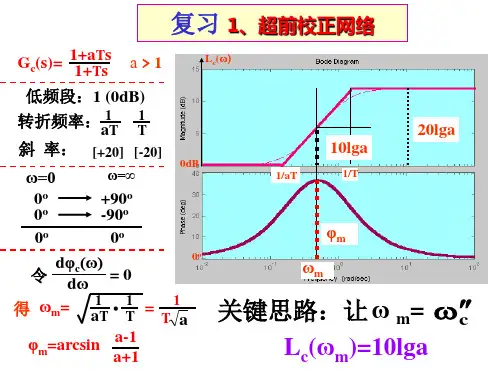
图6-12(b )所示网络传递函数为1)()1)(1()(212211*********++++++=s C R C R C R s C C R R s C R s C R s G c 11112211++++=s aT s T s a T s T (6-9) 式中 111T C R = ;222T C R =21212211aT aT C R C R C R +=++, (1>a ) 式中迟后校正部分为)1()1(22++s aT s T ;超前校正部分为)1()1(11++s aT s T 。
其对数频率特性曲线如图6-13所示。
由图可见,在频率ω由零增加到1ω的频段内,该网络呈现积分性质,具有迟后相角。
也就是说,在0~1ω频段里,相角迟后-超前网络具有单独的迟后校正特性;而在1ω~∞频段内,呈现微分性质,具有超前相角。
所以它将起单独的超前校正作用。
不难计算,对应相角等于零处的频率1ω为 2111T T =ω (6-10)二、串联迟后-超前校正应用串联迟后-超前校正设计,实际上是综合地应用串联迟后校正与串联超前校正的设计方法。
当未校正系统不稳定,且校正后系统对响应速度、相角裕量和稳态精度的要求均较高时,以采用串联迟后-超前校正为宜。
利用迟后-超前网络的超前部分来增大系统的相角裕量,同时利用迟后部分来改善系统的稳态性能或动态性能。
下面举例说明串联迟后-超前校正设计的一般步骤。
【例6-4】 设单位反馈系统,其开环传递函数为)15.0)(1()(++=s s s K s G 要求:(1)开环放大系数110-=s K ;(2)相角裕量︒=50γ;(3)幅值裕量dB h 10=;试确定串联迟后-超前校正网络的传递函数)(s G c 。



串联超前校正简单的超前网络若在系统的前向通路上(一般是串联于两级放大器之间),就构成了串联超前校正。
给系统串入串联超前校正,减少对数幅频特性在幅值穿越频率上的负斜率,可以有效地改善原系统的平稳性和稳定性,并可以提高系统的频带宽度,对快速性也将产生有利的影响,但是超前校正很难使原系统的低频段特性得到改善。
如果采取进一步开环增益的办法,使低频段上移,则系统的平稳性有所下移;幅频段过分上移,还会大大削弱系统干扰能力。
故超前校正对提高系统稳态精度的作用是很小的。
利用Bode 图设计超前校正网络超前校正的基本原理是利用超前网络的相位特性去增大系统的相位裕度,以改善系统的瞬态响应,具体设计步骤如下。
(1)求出满足稳态指标的开环放大系数K 值。
(2)根据求得的K 值,画出未校正系统的Bode 图,并计算出其幅值穿越频率c ω、相位裕度γ、幅度裕度g K 。
(3)确定需要对系统增加的相位超前m ϕ,m ϕ可表示为m ϕ=∆--γγ'式中,'γ 和γ 分别表示期望的相位裕度和未校正系统(原系统)的相位裕度,∆为增加超前网络后使幅值穿越频率向右方移动所带来的原系统相位的滞后量,一般该滞后量为 5~12。
(4)确定α值。
(5)确定校正后系统的幅值穿越频率'c ω。
为了最大限度利用超前网络的相位超前量。
'c ω应与m ω相重合,即 'c ω 应选在未校正系统的αωlg 10)(-=L 处。
(6)确定校正装置的传递函数。
令)/(1'αωωT c m ==,从而求出超前校正为了的两个转折频率 ⎩⎨⎧==T T αωω1112由此得出校正装置具有的传递函数为111121)(++=++=Ts Ts s sG s αωω(7)验证校正后系统的相位裕度γ。
MATLAB ProgramK0=1000;n1=1;d1=([1 0],[1 2]); sope= tf(K0*n1,d1);[mag,phase,w] =bode(sope);gama=45;[mu,pu]=bode(sope,w); gam=gama*pi/180;alfa=(1-sin(gam))/(1+sin(gam));adb=20*log10(mu);am=10*log10(alfa); ca=adb+am;wc=spline(adb,w,am); T=1/(wc*sqrt(alfa));alfat=alfa*T;Gc=tf([T 1],[alfat 1])MATLAB ProgramK0=1000;n1=1;d1=conv([1 0],[1 2]); S1=tf(K0*n1,d1);N2=[0.04916 1];d2=[0.008434 1]; S2=tf(n2,d2);sope=s1*s2;[mag,phase,w]=bode(sope);Margin(mag,phase,w);。

设 计 任 务题目: 超前校正一、设计内容设某控制系统不可变部分的传递函数为)11.0)(1001.0()(0++=s s s K s G ,要求该系统有如下性能指标:1)响应匀速信号r(t)=1R t 的稳态误差不大于0.0011R ,其中1R 为常量;2)剪切频率ωc =165rad/s ;3)相角裕度045γ≥;4)幅值裕度20lg g K ≥15dB 。
二、设计要求试应用频率响应法确定串联超前校正参数要求方法一用带惯性的PD 控制器实现串联超前校正方案1)劳斯判据判定未校正系统的稳定性,确定校正环节的传递函数模型。
2)计算校正系统的开环增益写出计算公式并通过MATLAB 编程计算,用MATLAB 画出未校正系统开环频率响应的Bode 图,计算未校正系统的剪切频率 ωc 写出计算公式并通过MATLAB 编程计算,相角裕度γ1写出计算公式,并通过MATLAB 编程计算。
3)根据给定的性能,计算要求校正后系统的剪切频率写出计算公式并通过MATLAB 编程计算,确定中频段宽度h 写出计算公式并通过MATLAB 编程计算。
4)计算最大超前相角m ϕ写出计算公式并通过MATLAB 编程计算。
5)计算串联超前校正参数a,T 写出计算公式并通过MATLAB 编程计算。
6)用MATLAB 验证性能四项指标,如果不符合修正校正参数继续验证,用劳斯判据和Nyquist 判据判定校正后系统稳定性。
7)设计校正环节的硬件参数,要求分别搭出无源校正和有源校正的电路图,确定电阻电容参数,用MATLAB 画出校正环节和最后的Bode 图,并进行对比说明。
要求方法二用PD 控制器实现串联超前校正方案1) 劳斯判据判定未校正系统的稳定性,确定校正环节的传递函数模型。
2) 根据要求求剪切频率ωc 计算出校正参数T 写出计算公式并通过MATLAB 编程计算。
3) 用MATLAB 验证性能四项指标,如果不符合修正校正参数继续验证,用劳斯判据和Nyquist 判据判定校正后系统稳定性。


第1篇一、实验目的1. 理解超前校正的原理及其在控制系统中的应用。
2. 掌握超前校正装置的设计方法。
3. 通过实验验证超前校正对系统性能的改善效果。
二、实验原理超前校正是一种常用的控制方法,通过在系统的前向通道中引入一个相位超前网络,来改善系统的动态性能。
超前校正能够提高系统的相角裕度和截止频率,从而改善系统的快速性和稳定性。
超前校正装置的传递函数一般形式为:\[ H(s) = \frac{1 + \frac{K}{T_{s}s}}{1 + \frac{T_{s}s}{K}} \]其中,\( K \) 为校正装置的增益,\( T_{s} \) 为校正装置的时间常数。
三、实验设备1. 控制系统实验平台2. 数据采集卡3. 计算机及仿真软件(如MATLAB/Simulink)4. 待校正系统四、实验步骤1. 搭建待校正系统模型:在仿真软件中搭建待校正系统的数学模型,包括系统的传递函数、输入信号等。
2. 分析系统性能:通过仿真软件分析待校正系统的性能,包括稳态误差、超调量、上升时间等。
3. 设计超前校正装置:根据待校正系统的性能要求,设计合适的超前校正装置参数。
4. 仿真验证:将设计好的超前校正装置添加到系统中,进行仿真验证,观察校正后的系统性能。
5. 实验数据分析:对实验数据进行分析,比较校正前后系统的性能差异。
五、实验内容1. 系统模型搭建:搭建一个简单的二阶系统模型,其传递函数为:\[ G(s) = \frac{1}{(s+1)(s+2)} \]2. 系统性能分析:分析该系统的稳态误差、超调量、上升时间等性能指标。
3. 设计超前校正装置:根据系统性能要求,设计一个超前校正装置,其传递函数为:\[ H(s) = \frac{1 + \frac{K}{T_{s}s}}{1 + \frac{T_{s}s}{K}} \]其中,\( K = 2 \),\( T_{s} = 0.5 \)。
4. 仿真验证:将设计好的超前校正装置添加到系统中,进行仿真验证,观察校正后的系统性能。
串联超前校正方法2超前网络的特性是相角超前,幅值增加。
串联超前校正的实质是将超前网络的最大超前角补在校正后系统开环频率特性的截止频率处,提高校正后系统的相角裕度和截止频率,从而改善系统的动态性能。
假设未校正系统的开环传递函数为)(0s G ,系统给定的稳态误差,截止频率,相角裕度和幅值裕度指标分别为***,,γωc ss e 和*h 。
设计超前校正装置的一般步骤可归纳如下:(1)根据给定稳态误差*ss e 的要求,确定系统的开环增益K 。
(2)根据已确定的开环增益K ,绘出未校正系统的对数幅频特性曲线,并求出截止频率0c ω和相角裕度0γ。
当*0c c ωω<,*0γγ<时可以考虑用超前校正。
(3)根据给定的相位裕度*γ,计算校正装置所应提供的最大相角超前量m ϕ,即)15~5(0︒︒+-=γγϕm (1)式中(5°~15°)是用于补偿引入超前校正装置,截止频率增大所导致的校正前系统的相角裕度的损失量。
若未校正系统的对数幅频特性在截止频率处的斜率为dec dB /40-,并不再向下转折时,可以取 8~5;若该频段斜率从dec dB /40-继续转折为dec dB /60-,甚至更负时,则补偿角应适当取大些。
注意:如果︒>60m ϕ,则用一级超前校正不能达到要求的*γ指标。
(4)根据所确定的最大超前相角m ϕ,求出相应的a 值,即m ma ϕϕsin 1sin 1-+= (2)(5)选定校正后系统的截止频率在a lg 10-处作水平线,与)(0ωL 相交于A '点,交点频率设为A 'ω。
取校正后系统的截止频率为{}*,max c A c ωωω'= (3)(6)确定校正装置的传递函数在选好的c ω处作垂直线,与)(0ωL 交于A 点;确定A 点关于dB 0线的镜像点B ,过点B 作dec dB /20+直线,与dB 0线交于C 点,对应频率为C ω;在CB 延长线上定D 点, 使Cc c D ωωωω=,在D 点将曲线改平,则对应超前校正装置的传递函数为1()1C CDsG s s ωω+=+ (4)(7)验算写出校正后系统的开环传递函数0()()()C G s G s G s =验算是否满足设计条件***h h c c ≥≥≥,,γγωω若不满足,返回(3),适当增加相角补偿量,重新设计直到达到要求。
完成一个控制系统的设计任务,往往需要经过理论和实践的反复比较才可以
得到比较合理的结构形式和满意的性能,在用分析法进行串联校正时,校正环节
的结构通常采用超前校正、滞后校正、超前滞后校正这三种类型,也就是工程上
常用的PID 调节器。
本次课设采用的超前超前校正的基本原理是利用超前相角
补偿系统的滞后相角,改善系统的动态性能,如增加相角裕度,提高系统稳定性
能等,而由于计算机技术的发展,matlab 在控制器设计,仿真和分析方面得到
广泛应用。
本次课设采用用Matlab 软件对系统进行了计算机仿真,分析未校正
系统的动态性能和超前校正后系统是否满足相应动态性能要求。
超前校正就是在前向通道中串联传递函数为:
()()()1
11G c ++⋅==Ts aTs a s R s C s 其中:
C R R R R T 2
121+= 1221>+=
R R R a 通常 a 为分度系数,T 叫时间常数,由式(2-1)可知,采用无源超前网络进行
串联校正 时,整个系统的开环增益要下降 a 倍,因此需要提高放大器增益交易
补偿. 如果对无源超前网络传递函数的衰减由放大器增 益所补偿,则
()1
1++=Ts aTs s aG c 上式称为超前校正装置的传递函数。
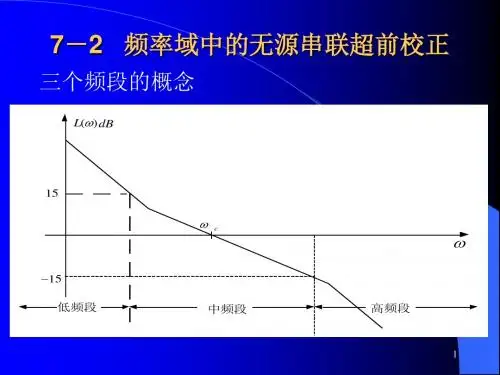
无源超前校正网络的对数频率特性如图6-4。
图6-4无源超前校正网络的对数频率特性
显然,超前校正对频率在1/aT 和1/T 之间的输入信号有微分作用,在该频
率范围内,输出信号相角比输入信号相角超前,超前网络的名称由此而得。
因此
超前校正的基本原理就是利用超前相角补偿系统的滞后相角,改善系统的动态性
能,如增加相位裕度,提高系统的稳定性等。
下面先求取超前校正的最大超前相角m ϕ及取得最大超前相角的频率m
ω,则像
频特性: ()ωϕc =arctanaT ω-arctanT ω ()()()221T
1d ωωωϕωT T a aT d c +-+= 当(),0=ωϕωd d e 则有: T a m 1=
ω 从而有:
a
a T a T T a aT 1arctan arctan 1arctan 1arctan m -=-=ϕ =11arcsin 21arctan 111arctan +-=-=+-a a a a a
a a a 既当T a m 1=ω时,超前相角最大为11arcsin m +-=a a ϕ,可以看出m
ϕ只与a 有关这一点对于超前校正是相当重要的
超前校正RC 网络图如图2。
图2超前校正RC 网络图
利用超前网络进行串联校正的基本原理,乃是利用超前网络相角超前特性。
只要正确地将超前网络的交接频率1/aT 和1/T 设置在待校正系统截止频率c ω的
两边,就可以使已校正系统的截止频率'c ω和相裕量满足性能指标要求,从而达
到改善系统动态性能的目的。
串联超前校正设计的一般步骤为
(1)根据稳态误差要求,确定开环增益K 。
(2)在已确定K 值条件下,计算未校正系统的相裕量。
(3)根据指标要求,确定在系统中需要增加的相角超前量。
(4)确定a 值及m L 值,在未校正系统的对数幅频特性曲线上找到幅值等于-m L 点所对应的频率,即为'c ω,这一频率为所选网络的c ω,并且在此频率上
将产生最大超前相角值m ϕ。
(5)确定超前网络的交接频率1ω=1/aT ,2ω=1/T 。
(6)验算。
二、原系统分析
设单位反馈系统的开环传递函数为:)
1001.0)(16.0)(1(5)(+++=s s s s s G 要求校正后系统的幅值裕度大于10dB ,相角裕度ο40≥γ,试设计串联超前
校正装置。
3.1 校正装置参数的确定
校正前截止频率s rad w c /73.1=,相角裕度γo o 402.16<-=,可知相角裕度不
满足要求,由此考虑加入串联超前校正系统。
为了满足校正后的系统的相角裕度︒≥40γ的条件,故需要加入 m θ='γ-[γ-(︒︒12~5)]=︒40-[︒-2.16-(︒︒12~5)], 然后再根据2.621
1sin
arg =+-=a a m θ求出7.15=a 。
跟据系统对相角裕度的要求,确定校正后系统的截止频率'c ω,由式10lg )(lg 20'c W A +α=0,由此可求得02.3c ='ω计算校正装置的时间常数T 。
由于a T W W m c 1
'==,由此可以解出T=0.084.
则校正装置的传递函数为()1084.01
3188.1s G c ++=s s
4.2 二次校正系统分析
如图6所示相角裕度o r 407.18<=,可知相角裕度不满足要求,由此考虑在次加入串联超前校正系统进行二次校正。
故需要加入m θ='γ-[γ-(︒︒12~5)]=o 50-[︒7.18-(︒︒12~5)], 然后再根据4.431
1sin arg =+-=a a m θ求出365.5=a 。
跟据系统对相角裕度的要求,确定校正后系统的截止频率"c ω
,由式10lg )''(lg 20c W A +α=0,由此可求得7.4''c =ω
计算校正装置的时间常数T 。
由于a
T W W m c 1''==,由此可以解出T=0.092. 则二次校正装置的传递函数为()1092.0149.0s "G c ++=
s s 校正后的传递函数为:
)
1092.0)(1084.0)(1001.0)(16.0)(1()149.0)(13188.1(5)(+++++++=s s s s s s s s G 如图7所示,由图可知h=12.1dB,ο8.43=γ满足系统要求
在设计超前校正装置校正时,要合理选择校正装置的参数,一般可以改善系统的动态性能。
从频率特性角度出发,可以利用将较高频段幅值下降20lg α、相位幅度较小的特性,减小系统的截止频率,提高相角裕度,从而提高了系统的稳定性。
但同时我们也应认识到串联校正装置本身所存在的缺陷和不足,以更好的把它应用于工程设计中。
如果在未校正系统的截止频率c ω附近,相频特性的变化率很大,即相角减小得很快,则采用单级串联校正效果将不大,这是因为随着校正后的截止频率'c
ω向高频段的移动,相角在c ω附近将减小得很快,于是在新的截止频率上便很难
得到足够大的相裕量。
在工程实践中一般不希望a 值很大,当a =20时,最大超
前角︒=60m ϕ,如果需要60°以上的超前相角时,可以考虑采用两个或两个以上的串联超前校正网络由隔离放大器串联在一起使用。
在这种情况下,串联超前校正提供的总超前相角等于各单独超前校正网络提供的超前相角之和。
(2)校正前系统的bode图
图2 (3)校正后系统的Bode图
图6 (4)二次校正后系统的Bode图
图7。