十三届三年级中环杯选拔赛
- 格式:pdf
- 大小:483.53 KB
- 文档页数:1

优客堂教育精品奥数班间隔趣谈(三)间隔趣谈(三)1、志愿者在一条长80米的路两旁植树,每8米植一棵,如果两头都植,需要()棵;如果两头不植,需要()棵;如果开始地方植一棵,终点不植,需要()棵。
2、同学们排队去春游,队伍从头到尾共20名小朋友,每两名小朋友之间的距离是1米,这个队伍长()米。
3、有一个圆形的水库,在水库的周围种满了樱花树,已知每两棵樱花树之间的距离都是6米,一共有80棵樱花树,这个水库的周长是()米。
4、在相距48米的两棵大树中间栽上7棵小树,要求间隔相等,树的间隔是()米。
5、一条街道两边从头到尾每隔6米埋一根电线杆,每两根电线杆中间植一棵树,街道的两边共植树20棵,街道长()米。
6、街心花园的周长是72米,每隔8米栽一棵杏树,一共需要()棵杏树。
7、一个圆形花坛,每隔4米摆一盆兰花,每两盆兰花中间摆1盆月季花,一共摆了60盆花,这个花坛的周长是()米。
8、有40个同学去操场围成一圈做体操,每相邻两人之间的距离是3米,他们围成的圆周长是()米。
如果圆的周长不变,每相邻两人之间的距离改为2米,需要()个同学才能围成这个圈。
9、在一个三角形池塘边植树,每边植6棵,最少植()棵。
10、(第十三届小机灵杯决赛)马戏团买来一些红气球、黄气球、蓝气球装饰圆形舞台,红气球40个正好全部用完,在每两个红气球中间装一个黄气球,结果少了3个,那么黄气球有()个。
在每个气球中间装一个蓝气球,结果正好装完,蓝气球有()个。
11、(《青少年科技报》2014年12月刊)陈庄小学有一个长60米,宽40米的小操场,四个顶点都种一棵树,长边上每隔10米种一棵,宽边上每隔8米种一棵,操场四周一共种了()棵。
12、(第十三届中环杯选拔赛)有六根木条。
各长50厘米,把它们首尾相连钉成一根很长的木条,每两根木条钉在一起的部分长10厘米,钉好后的木条长()厘米。
13、(2013年春蕾杯决赛)一个正方形的操场,每边都种13棵树,四个角都种,一共种了()棵。
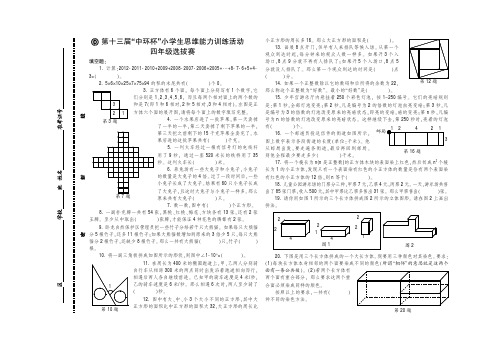

第十三届“中环杯”小学生思维能力训练活动五年级选拔赛1.计算:31.3×7.7+11×8.85+0.368×230=()。
2.宠物商店有狃狸犬和西施犬共2012只,其中母犬1110只,狐狸犬1506 只,公西施犬202只。
那么母狐狸犬有_( )只。
3.一个数A为质数,并且A+14, A+18, A+32, A+36也是质数。
那A的值是( )4.一个口袋中有50个编上号码的相同的小球,其中编号为1,2,3,4,5的小球分别有2,6,10,12,20个。
任意从口袋中取球,至少要取出()个小球,才能保证其中至少有7个号码相同的小球。
5.表格中定义了关于“*”的运算,如3*4=2。
(1*2)*(1*2)*……(1*2)=()。
共2012 个(1*2)6.数一数,图中共有()个三角形。
7.若干个学生去买蛋糕,若每人买K块,则蛋糕店还剩下6块蛋糕;若每人买8块,则最后一名学生只能买到1块蛋糕。
那么蛋糕店共有蛋糕()块。
8.—张正方形纸,如图所示折叠后,构成的图形中,角x的度数是()。
9.A、B两地相距66千米,甲、丙两人从A地向B地行走,乙从B地向AI地行走。
甲每小时行12千米,乙每小时行10千米,丙每小时行8千米。
三人同时出发()小时后, 乙刚好走到甲、丙两人距离的中点。
10.有()个形如abcdabcd的数能被18769 整除。
11.小明带24个自制的纪念品去伦敦奥运会卖。
早上每个纪念品卖7英镑,卖出的纪念品不到总数的一半。
下午他对每个纪念品的价格进行打折,折后的价格仍是—个整数。
下午他卖完了剩下的纪念品。
全天共收入120英镑。
那么早上他卖出了()个纪念品。
12.如图,在一个四边形ABCD中,AC,BD相交于点O。
作三角形DBC的高DE,联结AE。
若三角形ABO的面积与三角形DCO的面积相等,且DC=17厘米,DE=15厘米,则阴影部分的面积为( )平方厘米。
13.五名选手在一次数学竞赛中共得414分;毎人得分互不相等且都是整数,并且其中得分最高的选手得了92分,那么得分最低的选手至少得()分,最多得()分。


2020年中环杯获奖名单(三年级组)准考证号姓名奖项0130006金洛羽一等奖0130056佟松翼一等奖0130069杨元睿一等奖0130072纪皓天一等奖0130099祝明睿一等奖0130137李昊扬一等奖0130140周睿阳一等奖0130185王旭扬一等奖0130190徐子晨一等奖0130254黄大卫一等奖0130315张成浩一等奖0130361诸哲言一等奖0130384张书笑一等奖0130394卫星一等奖0130473杨镇一等奖0130523陈方旭一等奖0130536阮欣妍一等奖0130547贾丁一等奖0130550孟钰轩一等奖0130647姚越一等奖0130706金鑫渝一等奖0130708陈栩越一等奖0130721陆宇一等奖0130766陈修毅一等奖0130769张在贺一等奖0130787陈奕鑫一等奖0130788郭文赋一等奖0130877吴星宇一等奖0130907黄崇瑞一等奖0130926周昀朗一等奖0430026朱一青一等奖0430069蒋昕灏一等奖0430071徐邦杰一等奖0430108许皓然一等奖0430113邓瑞宁一等奖0430120黄首鑫一等奖0530042林光濠一等奖0530227潘嘉诚一等奖1630051杨子田一等奖1630052刘棋騵一等奖2930025吕锐一等奖2930026张黛凝一等奖2930059曹鸿生一等奖0130004李尚荣二等奖0130015舒胤嘉二等奖0130024庄子涵二等奖0130029李嘉安二等奖0130036陈一臻二等奖0130065薛睿涵二等奖0130066季庄喆二等奖0130074王舒涵二等奖0130079王淳稷二等奖0130157黄瀚卿二等奖0130165黄文远二等奖0130169陶安泽二等奖0130171方炜麟二等奖0130178黄子宸二等奖0130196徐天羿二等奖。
第十五届“中环杯”小学生思维能力训练活动三年级选拔赛1.计算:3×995+4×996+5×997+6×998+7×999-4985×3=__________2.一个数除以20的商是10,余数是10,这个数为__________3.如图是一个美术馆的俯视图,每个“×”表示A 、B 、C 、D 四人中的一个人,在美术馆中央是一根大石柱。
已知A 看不到任何人,B 只能看到C ,C 既可以看到B 也可以看到D ,D 只能看到C 。
那么,__________在P 点(填A 、B 、C 或D )A B B A A A B C CD如图1如图2如图3如图44.甲、乙两人相约去餐厅吃饭,由于这家餐厅生意火爆,所以甲到了之后就先去拿了一个等位号码,顺便等乙。
乙过了一会儿也到达餐厅,但是他没有看到甲,所以也去拿了一个等位号码。
等位的时候,乙看到了甲,两人拿出了等位号码,发现这两个号码的数码是顺序相反的两位数,而且两个号码的数码和(比如:数字23的数码和为2+3=5)都是8,而乙的号码比甲大18。
则甲的号码为__________5.将1~9这9个数分别填入图中的圆圈内,使得每个三角形(共7个)的3个顶点上的数之和都等于15。
现在已经填好了其中的3个,则标有“☆”的圆圈内应填__________6.10个学生(其中一个是队长,9个是队员)组队参加数学比赛,结果拿了第一名。
组委会决定颁发给队员每人200元奖金,队长比全队10名选手所获得的平均奖金还多90元。
则队长所获得的奖金为__________元。
7.森林里的小动物们外出郊游,它们排成了一列长40米的队伍,以每秒钟3米的速度前进。
小兔子有事要从排尾赶到排头,并立即返回排尾。
小兔的速度为每秒钟5米,那么经过__________秒钟,小兔可以返回排尾。
8.将4×4的大正方形切割为16个1×1的小正方形,擦去其中的两条线段,得到如图所示图形。
第十三届“中环杯”中小学生思维能力训练活动三年级选拔赛答案填空题1. 【答案】55555()()()()()()()()432432432432432432=34567+43675+56734+67453+753465310+410+510+610+7+410+310+610+710+5=+510+610+710+310+4+610+710+410+510+35+710+510+310+410+6=3+4+5+6+710+10+10+10+1÷⎡⎤⨯⨯⨯⨯⨯⨯⨯⨯⎢⎥⎢⎥⨯⨯⨯⨯⨯⨯⨯⨯÷⎢⎥⎢⎥⨯⨯⨯⨯⎣⎦⨯原式5=25111115=55555÷⨯÷2. 【答案】34由()()2A B A B A B *=+⨯-可知:()()757257517234*=+⨯⨯-=⨯=。
3. 【答案】5510+9+8+7+6+5+4+3+2+1=55(次)4. 【答案】74被3除余2的数有2,5,8,11,14,……其中14又能被5除余4,并且满足条件的最小的,而[3,5]=15,所以141529+=,291544+=,441559+=,591574+=满足了被7除余4这个条件,并且是最小的,因此是74。
5. 【答案】1234887用枚举法可以写出六个数,然后进行比较。
1123487,1223487,1233487,1234487,1234887,1234877,这就不难得到最大的数了。
出规律,212条直线最多能形成的交点数是1+2+3+……+211,得22366。
7. 【答案】223观察数列,不难发现它们以六个数字为周期不断重复,前六个数字之和为34526727+++++=。
50682÷= ,即前50个数字之和为 2787223⨯+=8.【答案】250重叠的部分长10厘米,一共重叠了615-=部分,那么钉好后木条总长是⨯-⨯-=厘米。
50610(61)2509.【答案】36,9椅子:90÷(2×4+3)=9(元)桌子:9×4=36(元)10.【答案】143(275-8+3)÷(1+2+3)=45(本)45×3+8=143(本)11.【答案】本题填法不唯一,以下是一种填法34 9 5612.【答案】17,80井深(1×5+3×4)÷(5-4)=17(米)绳子长(17-1)×5=80(米)13.【答案】14设面积最小的正方形面积为1,则面积为1的有6个,面积为2的有4个,面积为4的有2个,面积为5的有2个。
姓名年级学校准考证号赛区考场联系电话-------------------装----------------------订----------------------线---------------------第十三届世界奥林匹克数学竞赛(中国区)选拔赛全国总决赛------------------------------------------------------------------------------------------------------------------------三年级初赛试卷(本试卷满分120分,考试时间75分钟)一、知识题。
(每题5分,共50分)1.估计一下()最接近自己的年龄。
A.500分B.500时C.500天D.500周2.在如下所示折叠的纸板栗中能找到()个直角。
A.5B.4C.3D.23.右图是一个正方体的展开图,展开图的面积是150平方厘米,展开图的周长是()厘米。
A.50B.60C.70D.804.机器人工厂有A、B两种机械。
A机械每分钟可以制造6个机器人,B机械每分钟可以制造2个机器人。
若A和B 机械同时开始制造机器人,那么B机械在制造出16个机器人时,A机械比B机械制造出的机器人多()个。
A.22B.13C.32D.485.已知带余除法算式:11÷()=()……3,那么除数和商的和是()。
A.6B.8C.6或9D.6或86.2015年女足世界杯A组球队如下:加拿大、中国、荷兰、新西兰,若每两个球队比赛一场,一共要踢()场比赛。
A.6B.8C.10D.127.将周长为36厘米的长方形,用剪刀沿下图虚线剪成的4个长方形的周长之和是()厘米。
A.36B.54C.72D.不确定8.大熊和春丽住在同一单元,一天他俩放学一起上楼梯回家,春丽家住5楼,大熊算了一下,自己的速度必须是小红的2倍,才能与春丽同时到达各自的家中,那么大熊家住()楼。
填空题:
1.计算:(34567+43675+56734+67453+75346)÷5=()。
2.若A*B 表示(A +2B )×(A -B ),则7*5=()。
3.一把钥匙只能开一把锁。
现在有10把不同的锁和11把不同的钥匙,如果要找出每把锁的钥匙,最多需要试()次才能把每把锁和每把钥匙都正确配对。
4.被3除余2,被5除余4,被7除余4的最小自然数是()。
5.在六位数123487的某一位数码后面再插入一个该数码,得到一个七位数。
所有这些七位数中,最大的是()。
6.在平面上画212条直线,这些直线最多能形成()个交点。
7.有一列数字,按345267345267…的顺序排列,前50个数字的和是()。
8.有六根木条,各长50厘米。
现要将它们依次首尾相接钉在一起,每两根木条中间钉在一起的部分长10厘米。
钉好后木条总长()厘米。
9.学校买了2张桌子和3把椅子,共付了99元。
一张桌子的价钱和4把椅子的价钱相等,一张桌子()元,一把椅子()元。
10.在书架上摆放着三层书共275本,第三层的书比第二层的3倍多8本,第一层比第二层的2倍少3本。
第三层上摆放着()本书。
11.将3,4,5,6,9这五个数填入下图中,使得圆周上四个数的和与每条直线上的三个数的和都相等。
12.用一根绳子测井深
绳子露出井外3米;把绳子折
五折去量,绳子距离井口还有1米。
井深是()米,绳长是()米。
13.如图,在方格纸上的14个格点处有14枚钉子,用橡皮筋套住其中的几枚钉子,可以构成三角形、正方形、梯形等几何图形。
那么,一共可以构成()个不同的正方形。
14.如图为一个花园,线段表示花园中供行人行第十三届“中环杯”小学生思维能力训练活动
三年级选拔赛
走的小路。
园林工人要为花园里的花草浇水。
如果要不重复地走遍每条小路,应该以()为入口,以()为出口。
15.如图所示图形的周长是()。
16.有A 、B 、C 、D 四个点从左向右依次排在一条直线上。
以这四个点为端点,可以组成6条线段。
已知这6条线段的长度分别是15、21、34、35、48、69(单位:毫米),那么线段BC 的长度是()毫米。
17.图A 是一个由125个小正方体组成的大正方体。
从这个大正方体中抽出一些小正方体,抽的方法是:从一个面到其对面所涉及到的小正方体都要抽掉。
图B 中黑色部分就是抽出后的情形。
则图B 中共抽出了()个小正方体。
18.一列队伍长600米,以每秒钟2米的速度行进。
一战士因事要从排尾赶
到排头,并立即返回排尾。
若他每秒钟走3米,那么往返共行()米。
19.一天,某医院的红十字标记被人不小心碰坏了,碎成了5块,如图1。
你能把它恢复成原状吗?请在图2上画出拼法。
20.右图是一个变形的红十字,一共分为六块区
域。
现在要用四种颜色对其染色,要求相邻的两块区域(有公共边的两块区域称为相邻)染成不同的颜色。
如果颜色能反复使用,那么一共有()种不同的染色方法。
第17题
F
第14题
题第13题
第15题。