平面体系的几何组成分析习题解答

第二章平面体系的几何组成分析多余约束的存在要影响体系的受力性能和变形性能，是有用的。

连接两刚片的两根不共线的链杆相当于一个单铰（瞬铰）的约束作用。

X 相当于（4— 1） =3个单铰，相当于 6个约束。

X 为链杆，去除二元体后剩下体系如题答图 所示，有一个自由度。

X AB 杆不能既作为刚片川的一部 分又作为刚片i 、n 连接链杆。

去除二元体 后剩下的体系如题答图所示，有一个自由 度。

2、单项选择题将三刚片组成无多余约束的几何不变体系，必要的约束数目是几个A 2B 3C 4D 6三刚片组成无多余约束的几何不变体系，其联结方式是A 以任意的三个铰相联C 以三对平行链杆相联 瞬变体系在一般荷载作用下A 产生很小的内力 C 产生很大的内力从一个无多余约束的几何不变体系上去除二元体后得到的新体系是A 无多余约束的几何不变体系B 有多余约束的几何不变体系练习题: 1、判断题多余约束是体系中不需要的约束。

瞬变体系在很小的荷载作用下会产生很大的内力，所以不能作为结构使用。

两根链杆的约束作用相当于一个单铰。

每一个无铰封闭框都有三个多余约束。

连接四个刚片的复铰相当于四个约束。

图示体系是由三个刚片用三个共线的铰 图示体系是由三个刚片用三个共线的铰A\、BABC 相连，故为瞬变体系。

ABC 相连，故为瞬变体系。

(C )(D )(C (D (C (C (C) ) ) ) )1、判断题题图CBC 杆使用两次。

将刚片川视以不在一条线上三个铰相联 以三个无穷远处的虚铰相联不产生内力 不存在静力解答C图示体系是 A 瞬变体系BC 无多余约束的几何不变体系C 几何可变体系图示体系属于A 静定结构几何瞬变体系B 超静定结构 题图C图示体系属于A 无多余约束的几何不变体系 C 有多余约束的几何可变体系 不能作为建筑结构使用的是无多余约束的几何不变体系 几何不变体系C一根链杆 (C有多余约束的几何不变体系 瞬变体系有多余约束的几何不变体系 几何可变体系图示体系是A 瞬变体系 BC 无多余约束的几何不变体系下列那个体系中的1点不是二元体 （B ） 有一个自由度和一个多余约束的可变体系有两个多余约束的几何不变体系 （C )2、单项选择题 D B 2.5 A 2.6 C 2.3 C 题图2.4 A D ____ D 铰A 是相当于两个单铰的复铰， 体系是三个刚片用四个单铰相连，用了 8 个约束，有两个多余约束。

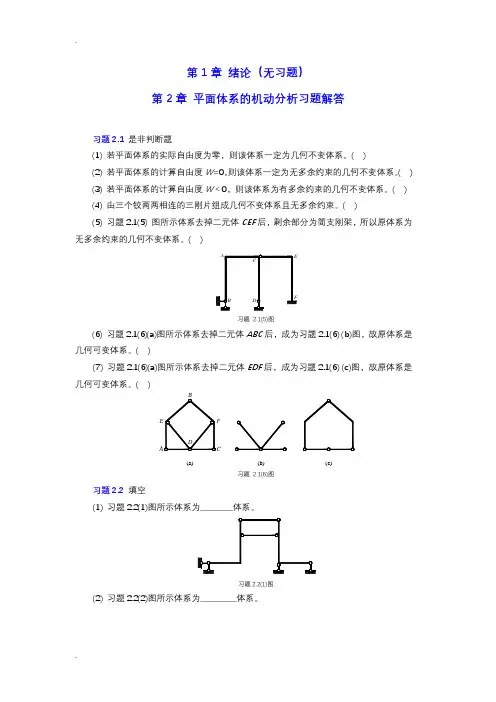
第一部分 平面体系的几何组成分析一、判断题：1、在任意荷载下，仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。

2、图中链杆1和2的交点O 可视为虚铰。

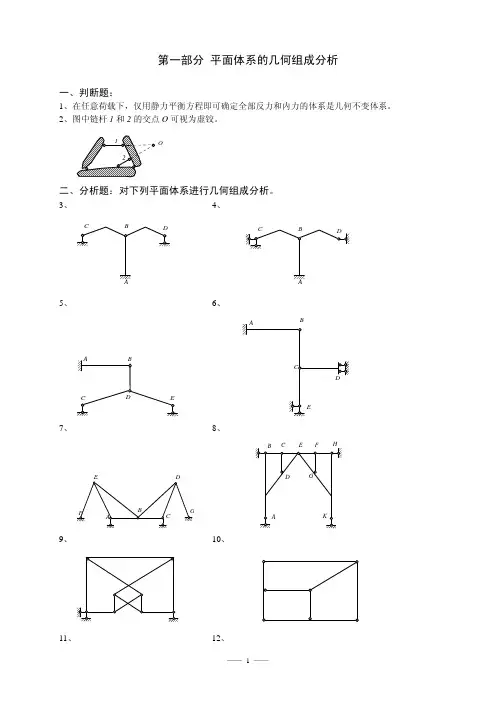
O二、分析题：对下列平面体系进行几何组成分析。

3、 4、ACDBAC DB5、 6、A CDBEABCDE7、 8、ABCD GE FA BCDEFGHK9、 10、11、 12、1234513、 14、15、 16、17、 18、19、 20、1245321、 22、124567831234523、 24、12345625、 26、27、 28、29、 30、31、 32、33、ACBDEF三、在下列体系中添加支承链杆，使之成为无多余约束的几何不变体系。

34、35、第二部分 静定结构内力计算一、判断题：1、静定结构的全部内力及反力，只根据平衡条件求得，且解答是唯一的。

2、静定结构受外界因素影响均产生内力，内力大小与杆件截面尺寸无关。

3、静定结构的几何特征是几何不变且无多余约束。

4、图(a)所示结构||M C =0。

(a)BCa aA ϕ2a2 (b)5、图(b)所示结构支座A 转动ϕ角，M AB = 0，R C = 0。

6、荷载作用在静定多跨梁的附属部分时，基本部分一般内力不为零。

7、图(c)所示静定结构，在竖向荷载作用下，AB 是基本部分，BC 是附属部分。

ABC(c)8、图(d)所示结构B 支座反力等于P /2(。

)↑9、图(e)所示结构中，当改变B 点链杆的方向（不通过A 铰）时，对该梁的影响是轴力有变化。

ＡＢ(e)10、在相同跨度及竖向荷载下，拱脚等高的三铰拱，水平推力随矢高减小而减小。

—— 1 ——11、图(f)所示桁架有9根零杆。

(f)a a a a(g)12、图(g)所示桁架有：=== 0。

N 1N 2N 313、图(h)所示桁架DE 杆的内力为零。

a a(h)14、图(i)所示对称桁架在对称荷载作用下，其零杆共有三根。

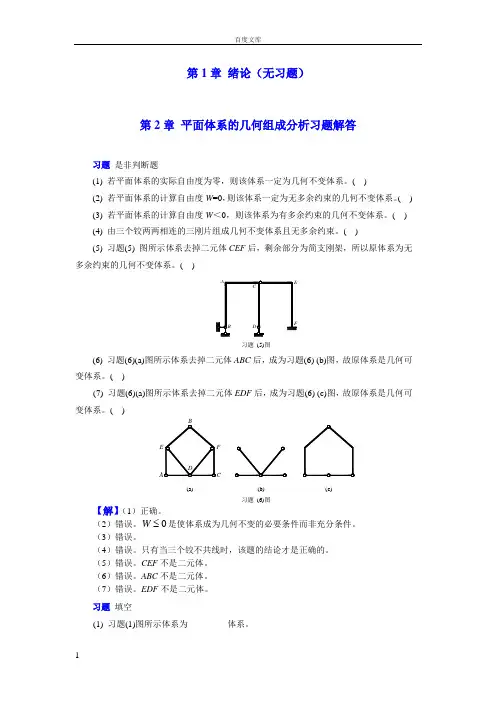
第1章 绪论（无习题）第2章 平面体系的几何组成分析习题解答习题 是非判断题(1) 若平面体系的实际自由度为零，则该体系一定为几何不变体系。

( )(2) 若平面体系的计算自由度W =0，则该体系一定为无多余约束的几何不变体系。

( ) (3) 若平面体系的计算自由度W ＜0，则该体系为有多余约束的几何不变体系。

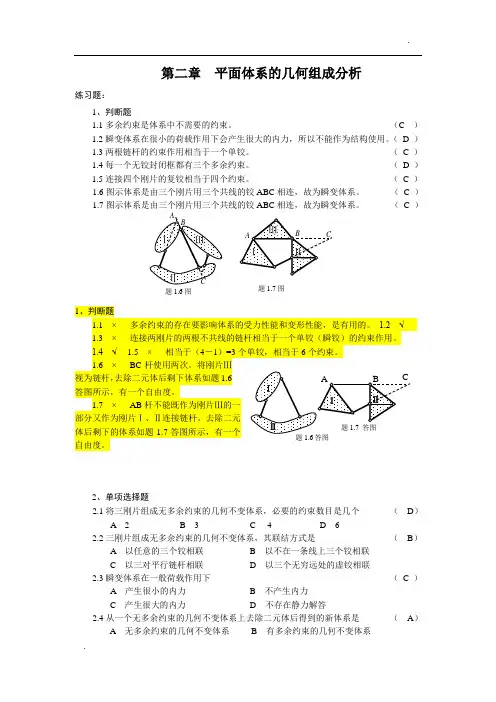
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。

( )(5) 习题(5) 图所示体系去掉二元体CEF 后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。

( )B DACEF习题 (5)图(6) 习题(6)(a)图所示体系去掉二元体ABC 后，成为习题(6) (b)图，故原体系是几何可变体系。

( )(7) 习题(6)(a)图所示体系去掉二元体EDF 后，成为习题(6) (c)图，故原体系是几何可变体系。

( )(a)(b)(c)D习题 (6)图【解】（1）正确。

（2）错误。

0W 是使体系成为几何不变的必要条件而非充分条件。

（3）错误。

（4）错误。

只有当三个铰不共线时，该题的结论才是正确的。

（5）错误。

CEF 不是二元体。

（6）错误。

ABC 不是二元体。

（7）错误。

EDF 不是二元体。

习题 填空(1) 习题(1)图所示体系为_________体系。

习题(1)图(2) 习题(2)图所示体系为__________体系。

习题2-2(2)图(3) 习题(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。

习题(3)图(4) 习题(4)图所示体系的多余约束个数为___________。

习题(4)图(5) 习题(5)图所示体系的多余约束个数为___________。

习题(5)图(6) 习题(6)图所示体系为_________体系，有_________个多余约束。

习题(6)图(7) 习题(7)图所示体系为_________体系，有_________个多余约束。

第二章 平面体系的几何组成分析练习题：1、判断题1.1多余约束是体系中不需要的约束。

（C ） 1.2瞬变体系在很小的荷载作用下会产生很大的力，所以不能作为结构使用。

（ D ） 1.3两根链杆的约束作用相当于一个单铰。

（ C ） 1.4每一个无铰封闭框都有三个多余约束。

（ D ） 1.5连接四个刚片的复铰相当于四个约束。

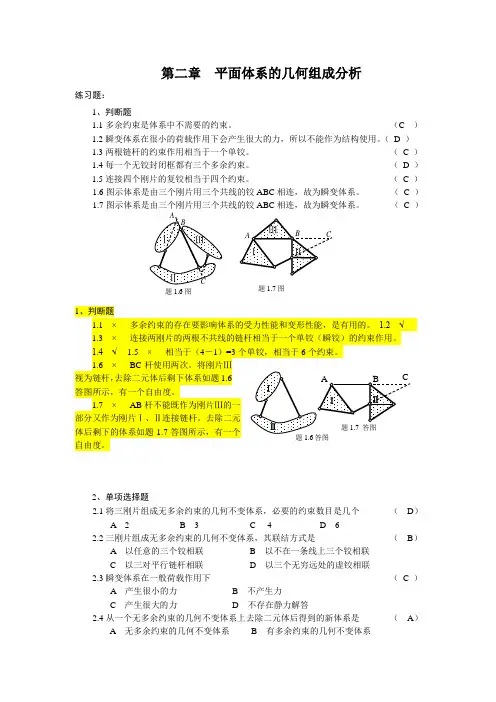
（ C ）1.6图示体系是由三个刚片用三个共线的铰ABC 相连，故为瞬变体系。

（ C ） 1.7图示体系是由三个刚片用三个共线的铰ABC 相连，故为瞬变体系。

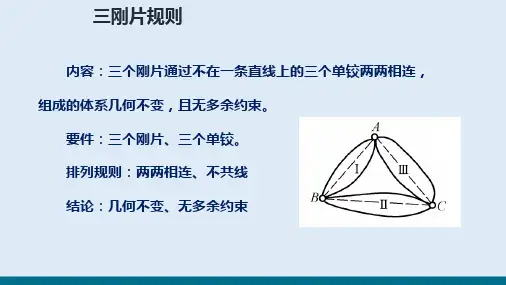
（ C ）2、单项选择题2.1将三刚片组成无多余约束的几何不变体系，必要的约束数目是几个（ D ）A 2B 3C4D 62.2三刚片组成无多余约束的几何不变体系，其联结方式是（ B ）A 以任意的三个铰相联B 以不在一条线上三个铰相联C 以三对平行链杆相联D 以三个无穷远处的虚铰相联 2.3瞬变体系在一般荷载作用下（ C ）A 产生很小的力B 不产生力C 产生很大的力D 不存在静力解答2.4从一个无多余约束的几何不变体系上去除二元体后得到的新体系是（ A ）A 无多余约束的几何不变体系B 有多余约束的几何不变体系题1.7图题1.6图C 几何可变体系D 几何瞬变体系 2.5图示体系属于（ A ）A 静定结构B 超静定结构C 常变体系D 瞬变体系2.6图示体系属于（C ）A 无多余约束的几何不变体系B 有多余约束的几何不变体系C有多余约束的几何可变体系D 瞬变体系 2.7不能作为建筑结构使用的是（ D ）A 无多余约束的几何不变体系B 有多余约束的几何不变体系C 几何不变体系D 几何可变体系 2.8一根链杆（ D ） A 可减少两个自由度B 有一个自由度 C有两个自由度D 可减少一个自由度2.9图示体系是（ D ）A 瞬变体系B有一个自由度和一个多余约束的可变体系C 无多余约束的几何不变体系2.10图示体系是（B ）A 瞬变体系B 有一个自由度和一个多余约束的可变体系C 无多余约束的几何不变体系D 有两个多余约束的几何不变体系 2.11 下列那个体系中的1点不是二元体（C ）题2.5图题2.9图题2.10图答图2.10 B 把刚片Ⅱ视为链杆，然后去 除二元体A ，剩下两个刚片用一个单铰相连，有一个自由度，而刚片Ⅰ中CD 杆是多余约束。

平面体系的几何组成分析(总分：100.00，做题时间：90分钟)一、{{B}}判断题{{/B}}(总题数：6，分数：12.00)1.下图所示体系为有一个多余约束的几何不变体系。

（分数：2.00）A.正确B.错误√解析：利用三刚片规则。

可选择AB、CD、EF作为刚片进行分析。

正确答案是无多余约束的几何不变体系。

2.下图所示体系中链杆1和2的交点O可称为虚铰。

（分数：2.00）A.正确B.错误√解析：3.自由度W≤0是体系保持几何不变的充分条件。

（分数：2.00）A.正确B.错误√解析：4.静定结构是无多余约束的几何不变体系，超静定结构是有多余约束的几何不变体系。

（分数：2.00）A.正确√B.错误解析：5.下图所示体系是几何不变体系，且无多余约束。

（分数：2.00）A.正确B.错误√解析：原体系为有一个多余约束的几何不变体系。

6.下图所示对称体系是几何瞬变体系。

（分数：2.00）A.正确√B.错误解析：如下图所示选取刚片，用三刚片规则分析，刚片Ⅰ与Ⅱ交于A点，刚片Ⅰ与Ⅲ交于B点，刚片Ⅱ与Ⅲ交于无穷远处C点，由于A、B的连线与连系刚片Ⅱ、Ⅲ的两杆平行。

根据无穷远点规则判断可知，该体系为几何瞬变体系。

[*]二、{{B}}填空题{{/B}}(总题数：6，分数：12.00)7.下图所示体系的几何组成为______体系。

（分数：2.00）填空项1:__________________ （正确答案：无多余约束的几何不变体系）解析：利用三刚片规则分析。

8.下图所示体系的几何组成为______，______。

（分数：2.00）填空项1:__________________ （正确答案：几何不变体系，无多余约束）解析：先选择基础为一个刚片，然后按“双藤摸瓜”方法找到另外两个刚片。

9.下图所示体系为几何______体系，多余约束数为______个。

（分数：2.00）填空项1:__________________ （正确答案：不变，1）解析：利用三刚片规则分析。

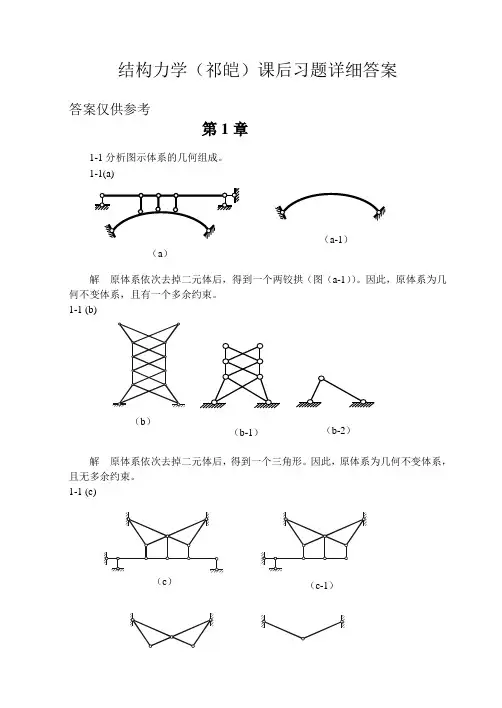
结构力学（祁皑）课后习题详细答案答案仅供参考第1章1-1分析图示体系的几何组成。

1-1(a)解 原体系依次去掉二元体后，得到一个两铰拱（图（a-1））。

因此，原体系为几何不变体系，且有一个多余约束。

1-1 (b)解 原体系依次去掉二元体后，得到一个三角形。

因此，原体系为几何不变体系，且无多余约束。

1-1 (c)（c-1）（a ）（a-1）（b ）（b-1）（b-2）（c-2） （c-3）解 原体系依次去掉二元体后，得到一个三角形。

因此，原体系为几何不变体系，且无多余约束。

1-1 (d)（d-1） （d-2） （d-3）解 原体系依次去掉二元体后，得到一个悬臂杆，如图（d-1）-（d-3）所示。

因此，原体系为几何不变体系，且无多余约束。

注意：这个题的二元体中有的是变了形的，分析要注意确认。

1-1 (e)解 原体系去掉最右边一个二元体后，得到（e-1）所示体系。

在该体系中，阴影所示的刚片与支链杆C 组成了一个以C 为顶点的二元体，也可以去掉，得到（e-2）所示体系。

在图（e-2）中阴影所示的刚片与基础只用两个链杆连接，很明显，这是一个几何可变体系，缺少一个必要约束。

因此，原体系为几何可变体系，缺少一个必要约束。

1-1 (f)解原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相连，符合几何不变体系的组成规律。

因此，可以将该刚片和相应的约束去掉只分析其余部分。

很明显，余下的部分（图（f-1））是一个几何不变体系，且无多余约束。

因此，原体系为几何不变体系，且无多余约束。

1-1 (g)（d ） （e ）（e-1）A（e-2）（f ）（f-1） （g ） （g-1） （g-2）解 原体系中阴影所示的刚片与体系的其它部分用三个链杆相连，符合几何不变体系的组成规律。

因此，可以将该刚片和相应的约束去掉，只分析其余部分。

余下的部分（图（g-1））在去掉一个二元体后，只剩下一个悬臂杆（图（g-2））。