当前位置：文档之家 › (完整版)对偶单纯形法详解

(完整版)对偶单纯形法详解

  • 格式：ppt
  • 大小：328.01 KB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

运筹学 对偶单纯形法

运筹学 对偶单纯形法
3.若所有akj’≥0( j = 1,2,…,n )，则原问题 无可行解,停止;否则,若有akj’<0 则选
=min{j’ / akj’┃akj’<0}=r’/akr’那么 xr为进基变量,转4； 4.以akr’为转轴元,作矩阵行变换使其变为1,该
列其他元变为0,转2。
2.对偶单纯形法
例3.2：求解线性规划问题：
1.线性规划对偶问题
对称形式： (P) Max z = cT x s.t. Ax ≤ b x ≥0 “Max -- ≤ ”
互为对偶 (D) Min f = bT y s.t. AT y ≥ c y ≥0 “Min-- ≥”
线性规划的对偶模型
原问题（或对偶问题） 约束条件右端项 目标函数变量的系数 目标函数 max 约 束 条 件 m个 ≤ ≥ = n个 变 量 ≥0 ≤0 无约束 对偶问题（或原问题） 目标函数变量的系数 约束条件右端项 目标函数 min m个 ≥0 ≤0 无约束 n个 ≥ ≤ = 约 束 条 件 变 量
否
所有aik
计算
0
否
是
Hale Waihona Puke 0 bi be min aik 0 aik aek
计算
j min aej 0 k < aej aek
以为中心元素进行迭代
以为中心元素进行迭代
单纯形法和对偶单纯形法步骤
2.对偶单纯形法 对偶单纯形法的适用范围 对偶单纯形法适合于解如下形式 的线性规划问题
0 x4 0 1 0 0 0 1 0 0 0 1 0 0
0 x5 0 0 1 0 -1 -1 1 -100 -1 1 1 -50
I
θ i 300 400 250 50 75

运筹学及其应用4.3 对偶单纯形法

运筹学及其应用4.3 对偶单纯形法
3
min w= 2x1+3x2+4x3+0x4+0x5 x1+2x2+ x3-x4＝ 1 2x1- x2+3x3– x5＝4 x1,x2,x3,x4,x5≥ 0
min w= 2x1+3x2+4x3+0x4+0x5 -x1-2x2- x3+x4＝ -1 -2x1+x2-3x3+x5＝ -4 x1,x2,x3,x4,x5≥ 0
4
234 000
0
x1 x2 x3 x4 -1 -2 -1
x4 x5 b 1 0 -1
max

2 −2
4 ，
−3

=
−1
0 x5 -2* 1 -3 0 1 -4
σ 234 000
0 x4 0 -2.5 0.5 1 -0.5 1
2 x1 1 -0.5 1.5 0 -0.5 2
σ 0 4 1 0 1 -4
步骤：(1)保持σj ≥ 0，j= 1,···,n，确定XB，建立计算表格； (2)判别XB = B-1b ≥ 0是否成立？ ①若成立，XB为最优基变量； ②若不成立，转(3)；
1
步骤：(1)保持σj ≥ 0，j= 1,···,n，确定XB，建立计算表格；
(2)判别XB = B-1b ≥ 0是否成立？ ①若成立，XB为最优基变量； ②若不成立，转(3)；
5
• 作业 • P81 1.12(1)
6
§3 对偶单纯形法
单纯形法：由 XB = B-1b ≥ 0，使σj ≥ 0，j = 1,···,m 对偶单纯形法：由σj ≥ 0(j= 1,···,n)，使XB = B-1b ≥ 0 相同点：都用于求解原问题

对偶单纯形法

对偶单纯形法
单纯形法迭代过程的实质是：在保持原问题可行性的前提下，驱使对偶问题从 不可行转变为可行的发展历程。
把上述思想移植到对偶问题上。
对偶单纯形法迭代过程的实质是：保持对偶问题的可行性（只要检验数≤0即可）， 通过改变对偶问题的可行基，使原问题由不可行变为可行。根据对偶理论，这两 个可行解就是原始和对偶问题的最优解。
例2.4.1 用对偶单纯形法求解下列线性规划问题。 min z = 15x1+24 x2 +5 x3
6 x2 + x3 ≥2
st.
5x1+2 x2 + x3 ≥1
x1 , x2 , x3 ≥0
解：把线性规划问题化为标准形式。
max z′ = －15x1－24 x2 － x3 +0 x4 +0 x5
-2/3是主元素， x3是换入变量。
ቤተ መጻሕፍቲ ባይዱj
－15 －24 － 5
CB
XB
b
x1
x2
x3
-24
x2 1/4
-5/4
1
0
表 11
0
0
x4
x5
-1/4 1/4
5
x3 1/2 15/2
0
1
1/2 -3/2
(cj－zj) 或 j
-15/2 0
0
-7/2 -3/2
由于原始，对偶都已经可行，所以，表11对应的解是最优解。
求极大为标准形式时
min j
c
j
arj
z
j
arj
0
cs zs ars
求极小为标准形式时
min j
z
j c arj
j
arj
0

第三章对偶单纯形法

第三章对偶单纯形法

··
≥ (c1,c2,…,cn)
y1，y2，…，ym≥0
m个变量，n个约束条件
2﹒约束条件全部为“=”的对偶
原问题：
max z=CX
max z=CX
max z=CX
AX＝b
等价
AX≤b AX≥b
AX≤b 等价 －AX≤－b
X≥0
min ω=(Y1,Y2) A
(Y1,Y2) －A Y1,Y2≥0
b －b
承租
出让代价应不低于 用同等数量的资源 自己生产的利润。
厂家能接受的条件：
出 用同让6等代y数价2量应的不y资低3 源于 2 5 y自1 己生2产y2的利y润3。 1
收购方的意愿：
min w 15 y 24 y 5 y
1
2
3
Ⅰ
Ⅱ
D
设备A
0
设备B
6
调试工序
1
5 15时 2 24时 1 5时
利润（元） 2
x1 0, x2 , x3 0, x4无限制max变S量个数5n y1 约4束y方2 程个6数yn3
2、求下列问题的对偶问题 min Z 2x1 3x2 5x3 x4
4x1 x2 3x3 2x4 5
s.t
3x1 2x2 7x4 2x1 3x2 4x3
4 x4
6
s.t
3﹒约束条件为“≥”的对偶
原问题：
max z=CX
max z=CX
对
AX≥b
等价
－AX≤ － b
偶
X≥0 min ω=Yb
对偶 问题
X≥0
问
题
min ω=Y1 (－ b)
YA ≥C Y≤0
令Y= － Y1

对偶单纯形法

对偶单纯形法
2x1 x2 3x3 4 x1 , x2 , x3 0
1. 换出变量的确定原则
常数列中最小的负元素所在的行所对应的基变量为换出变量.
p11-1
§3.4 灵敏度分析
运筹学
灵敏度分析——研究系数变化对最优解的影响.
一、改变价值向量
在最终表内, cr的变化只引起检验数的变化, 需重新计算检验数.
§3.3 对偶单纯形法
运筹学
一、对偶单纯形法与单纯形法的区别
对 运用对偶单纯形法时, 不需要引入人工变量, 但必须先给 定原问题的一个对偶可行基本解.
二、对偶单纯形法的求解方法
▲ 以求解下述线性规划 问题为例
min z 2x1 3x2 4x3 s.t. x1 2x2 x3 3
二、改变资源向量
在最终表内, br的变化只引起右端项的变化, 需重新计算右端项. 利用B-1(b+b).
三、改变A中的一列
通常是非基变量所对应的列, 需重新计算检验数.
四、增加一个新的约束条件
五、增加一个新的变量
p11-2
运筹学
作业：P81第1.12题之（2）； 第1.13题
p11-3

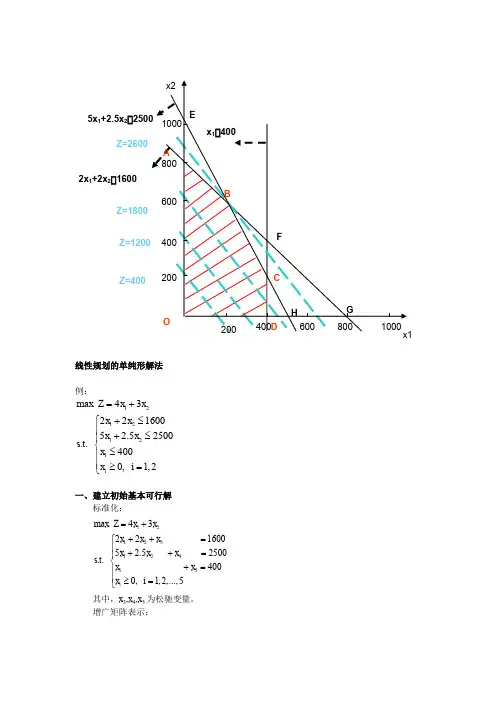
单纯形解法与对偶解法

单纯形解法与对偶解法

线性规划的单纯形解法 例：1212121max Z 432216005 2.52500.. 4000, 1,2i x x x x x x s t x x i =++≤⎧⎪+≤⎪⎨≤⎪⎪≥=⎩一、建立初始基本可行解标准化：1212312415max Z 4322 16005 2.5 2500.. 4000, 1,2,...,5i x x x x x x x x s t x x x i =+++=⎧⎪++=⎪⎨+=⎪⎪≥=⎩ 其中，x 3,x 4,x 5为松驰变量。

增广矩阵表示：2x 1+2x 2 1600Z=4005x 1+2.5x 212345 2 2 1 0 0 16005 2.5 0 1 0 2500 1 0 0 0 1 400x x x x x b ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦初始可行基：1 1 0 00 1 00 0 1B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦基变量可用非基变量表示成：3124125116002-225005 2.5400x x x x x x x x=-⎧⎪=--⎨⎪=-⎩ 令非基变量x 1=x 2=0，得初始可行解：X=[0,0,1600,2500,400]，对应于可行域的O 点。

相应的Z 值为0二、解的最优性检验规划判断的方法是检查目标函数中是否还有正的系数。

Z=4x 1+3x 2+0 因此，如果将这两个非基变量中的任意一个变成基变量，也就是使该变量的取值由零变为正值，都有可能使目标函数值增加，因此原来的解不是最优解。

三、第一次迭代（基变换） 1.确定换入变量一般选取价值系数大的那个为入基变量。

这里选择x 1为入基变量。

2.确定换出变量确定入基变量，同时要确定换出变量，其原则是使得到的新的基本解同时是可行解。

分析如下：令x 2=0（x 2仍为非基变量），得：3141511600225005400x x x x x x=-⎧⎪=-⎨⎪=-⎩ 随着x 1的增加，x 3, x 4, x 5的值就会逐渐变小，但始终应保持非负。

单纯形法和对偶问题

单纯形法和对偶问题
第六章 单纯形法的灵敏度分析与对偶问题
• • • •
§1 §2 §3 §4
单纯形表的灵敏度分析 线性规划的对偶问题 对偶规划的基本性质 对偶单纯形法
管
理
运
筹
学
1
单纯形表
管
理
运
筹
学
2
§1 单纯形表的灵敏度分析
一、目标函数中变量系数Ck灵敏度分析（在什么范围内变化， 最优解不变，与第二章，第三章联系起来） 在线性规划的求解过程中，目标函数系数的变动将会影响检 验数的取值，但是，当目标函数的系数的变动不破坏最优判 别准则时，原最优解不变，否则，原最优解将发生变化，要 设法求出新的最优解。下面我们具体的分析 1.在最终的单纯形表里，X k是非基变量 由于约束方程系数增广矩阵在迭代中只是其本身的行的初等 变换与Ck没有任何关系， 所以当Ck变成Ck+ Ck时，在最终单纯形表中其系数的增广矩 阵不变，又因为Xk是非基变量，所以基变量的目标函数的系 数不变，即CB不变，可知Zk也不变，只是Ck变成了Ck+ Ck。 这时 K= Ck-Zk就变成了Ck+ Ck- Zk= K+ Ck。要使原来的 最优解仍为最优解，只要 K+ Ck≤0即可，也就是Ck的增量 Ck≤- K。
由于单纯形表的迭代是约束方程的增广矩阵的行变换，Pk变成Pk’仅仅影响最终单纯形表上第k列
数据，包括Xk的系数列、Zk以及 ，这时最终单纯形表上的Xk的系数列就变成了B-1Pj’,而Zk就变成 k
CBB-1Pk’，新的检验数 迭代以求出最优。 例 以第二章例1为基础，设该厂除了生产Ι，Ⅱ种产品外，现在试制成一个新产品Ⅲ，已知生产产品
实际意义可以描述为：设备台时数在250与325之间变化，则设备台时

对偶单纯形法

对偶单纯形法

3x2 2x2
x4 x5
x7 3
6
用单纯形 法求解
x1, x2 , x3 , x4 , x5 0
对偶单纯形法的优点：
1、不需要人工变量；
2、当变量多于约束时，用对偶单 纯形法可减少迭代次数；
3、在灵敏度分析中，有时需要用对 偶单纯形法处理简化。
注意：对偶单纯形法仅限于初始基B对应
X（0）为基本可行 解的X（条0）件为？最优解的 条件？
B-1b≥0 C CBB1 A 0
原问题最优解条件
令Y=CBB-1，代入原问题最优解条件，→YA≥C
min Yb
YA C Y无符号限制
取基本解X1 B1b,0
保证对偶问题的可行性，逐
步改进原问题的可行性，求
x1 x3 2
s.t

x2
2x3
5
x1，x2，x3 0
若取初始基B1 P4，P5
则关于B1的标准型为
max Z 4x1 3x2 8x3
不s可.t 行 x1x2
x3 2x3

x4
2 x5 5
x1，x2，x3 , x4 , x5 0
且由对偶理论知，Y0 CB B 1为（D）的最优解
对偶单纯形法步骤：
1. 列出初始单纯形表，检查b 列的数字若都为非负， 则已得到最优解，停止计算，若b列的数字中至少 有一个负分量，转第二步。
2. 确定出基变量
按 min B1b i B1b i 0 B1b l ,对应的基变量法： 求max Z x6 Mx9

2x2 x3 x4 x5
x9 1

对偶单纯形法(经典运筹学)

对偶单纯形法(经典运筹学)

引进人工变量 x6，x7 max Z 2 x1 x 2 Mx6 Mx7 3x1 x 2 x3 x6 3 4 x 3 x x x 6 2 4 7 s.t 1 x1 2 x 2 x5 3 x1 , x 2 , x3 , x 4 , x5 0
3 6 最优解 X （ ，， 0， 0， 0 ） 5 5
最优值 Z 12
5
对偶单纯形法步骤：
1、找出一个初始对偶可行解。 即找出一个基B，
把原问题写成该基的典则形式时，目标函数的系数均≤0
2、判断： （1）若B-1b≥0，则得到最优解 （2）若B-1b≥0， 记B 1b b1 , b2 , , bm
m ax Z 2 x1 x 2 3 x1 x 2 x3 3 4 x 3x x 6 1 2 4 s.t 基 B的典则形式 x1 2 x 2 x5 3 x1 , x 2 , x3 , x 4 , x5 0
取基B P 3, P 4,P 5
解：问题化为标准型 max Z 2 x1 x 2 5 x1 x 2 x3 2 x 2 x3 x 4 5 s.t 6x xx 9 xx 2 2 6 x3 3 5 5 9 44 x1 , x 2 , x3，x 4，x5 0
1、确定出基变量： 设br =min{bi | bi <0} 则取br所在行的基变量 为出基变量 即取X4为出基变量 2、确定入基变量： 原则： 保持检验行系数≤0
i i0 设 min | a ri 0 a ri a ri 0
1 21 3
X1 检 -2/3 X3 -5/3 X2 4/3 X5 -5/3 X1 检 0 X3 0 X3 X4 0 -1/3 1 0 0

对偶单纯形法详解课件

对偶单纯形法详解课件

终止准则
算法终止的准则有多种，如达到预设的 最大迭代次数、解的变化小于预设阈值 等。
VS
终止判断
在每次迭代后，需要判断是否满足终止准 则，如果满足则算法终止，否则继续迭代 。
04 对偶单纯形法的优化策略
预处理技术
预处理技术
通过预处理，可以消除原问题中的冗 余约束，简化问题规模，提高求解效 率。
线性规划问题的转化
对偶单纯形法详解课 件
目录
CONTENTS
• 对偶单纯形法简介 • 对偶单纯形法的基本原理 • 对偶单纯形法的实现步骤 • 对偶单纯形法的优化策略 • 对偶单纯形法的案例分析 • 对偶单纯形法的展望与未来发展方向
01 对偶单纯形法简介
对偶问题的定义
对偶问题是指原问题的一个等价形式，其目标函数和约束条 件与原问题互为对偶。在优化问题中，对偶问题通常用于求 解原问题的最优解。
对偶单纯形法的应用场景
对偶单纯形法广泛应用于各种优化问题，如线性规划、整数规划、二次规划等。 它适用于求解大规模优化问题，并且具有较高的计算效率和精度。
在实际应用中，对偶单纯形法可以与其他优化算法结合使用，如梯度下降法、共 轭梯度法等，以提高求解效率和精度。同时，对偶单纯形法也可以用于解决一些 复杂的组合优化问题，如旅行商问题、背包问题等。
对偶问题的形式取决于原问题的类型和约束条件。例如，线 性规划的对偶问题就是将原问题的目标函数和约束条件进行 线性变换，得到一个新的优化问题。
对偶单纯形法的概念
对偶单纯形法是一种求解线性规划的方法，它利用对偶问 题的性质，通过迭代和交换变量的方式，逐步逼近最优解 。
在对偶单纯形法中，每次迭代都包括两个步骤：一是根据 对偶问题的最优解更新原问题的解；二是根据原问题的最 优解更新对偶问题的解。这两个步骤交替进行，直到达到 最优解或满足一定的停止准则。

运筹学对偶单纯形法

运筹学对偶单纯形法

则原问题无可行解。
例: 用对偶单纯形法求解线性规划问题：
min w 15y 1 24y 2 5y 3
s.t 6y 2 y 3 2 y1 , y 2 , y 3 0 5y 1 2y 2 y 3 1
对偶问题的 初始可行基

maxw w 15 15y1 max 1 24y2 2 5 y3 3 y y 2 s.ts.t 6 y2 y 2 3 4 2 3 4 5y y 2 y y y 1 -5 2 y y y 1 1 2 3 5 1 2 3 5 ,2y , , 5y y1y , 1y ,2 ,y 00 5
xk a1s …
… …
xn a1n …
…
0
a1, m+1
…
… … … … … … 即不可能存在 xj 0(j=1, …,n)的解，
bl l 故原问题无可行解，
… … … 0 0 … … 0 0 xm cj－zj
bm
x
0
…
1
…
0 … 1 0
a l,m+1 …
…
alk …
…
aln …
此时对偶问题的目标函数值无界。
-4 x3
-1/5
0 x4
-2/5
0 x5
1/5
1 0
0
7/5
-3/5
-1/5
-8/5
-2/5
-1/5
0
bi≥0, σj≤0得到最优解为：
X*=(11/5, 2/5,0,0,0）T 对偶问题最优解为：
Y ( y , y ) (8 / 5,1 / 5)
* * 1 * T 2
T

对偶单纯形法

对偶单纯形法

x 1 , x 2 , , x n x

是原问题 LP 的可行解，并且当扩充问题的最优
就是原问题 LP 的最优解． 值与大 M 无关时， x
以上通过构造扩充问题运用对偶单纯形法求解 LP 的做法与 单纯形法中的大 M 法相似。
例 3.3.2
用对偶单纯形法求解下列线性规划问题：
x j 0, j 1, 2, , 6
把扩充问题的数据列入表 3-7 中，并计算各检验数 j ．

2
2
0
0
0
0
基
b
8
x1
1
x2
4
x3
1
x4
1
x5
0
1
x6
0 0
1
x4 x5 x6
6
M
1
2
2
0
0
1
2
1
2
1
0 0
0 0
j
0
0
因 1 2 ，故此时的基本解还不是对偶可行的．选择 x1 为换入变量， x6 为换出 变量，即以 a31 1 为主元素进行变换，得到表 3.8．
j j
am1, j am1,k
k
其中 j 是变换后在新基下的检验数． 当 j n 1 时，am1, j 1 ， 而 am1,k 1 ， 故有 j j k 0 ；而当 j n 1 时， j 0, am1, j 0 ，故有 j 0 ．
min z 2 x1 2 x2 s.t. x1 4 x2 x3 8 x1 2 x2 2 x3 6 x1 , x2 , x3 0
解 式：
引入剩余变量 x4 和松弛变量 x5 ，把问题化为标准形

对偶单纯形法(经典运筹学)

对偶单纯形法(经典运筹学)
基本解 X 0， 0， 3 ， 6， 3
X1 X2 X3 X4 X5 检 X3 -2 -1 0 -3 -1 1 0 0 0 0 Z -3
X4
X5
-4 -3 0
1 2 0
1
0
0
1
-6
3
不 可 行
即max Z 2 x1 x2
3 3x1 x 2 x3 4 x 3x x4 6 1 2 s.t x5 3 x1 2 x 2 x1 , x 2 , x3 , x 4 , x5 0
-1/3 0 -1/3 0 2/3 1
X 3 X4 X5 0 -3/5 -2/5 Z+12/5 1 -1 -1 0
X2 0 X1 1
1 0
0 0
1/5 4/5 6/5 -2/5 -3/5 3/5
3 6 最优解X （ ，， 0， 0， 0 ） 5 5 最优值Z 12 5
则取xi0 为入基变量
1
1
令X N 0 得X B B b 0 得基本可行解 X 1 B b,0
1
1

1 、若所有的检验数 CN B 1 N 0 , 则X 1为最优解
2、检验数 C N C B B 1 N中存在一个分量 0, 且该分量对应的列 向量中所有的分量 0, 则目标函数值在可行解 域内无上界
1、确定出基变量： 设br =min{bi | bi <0} 则取br所在行的基变量 为出基变量 即取X4为出基变量 2、确定入基变量： 原则： 保持检验行系数≤0
i i0 设 min | a ri 0 a ri a ri 0
1 21 3
X1 检 -2/3 X3 -5/3 X2 4/3 X5 -5/3 X1 检 0 X3 0 X3 X4 0 -1/3 1 0 0

运筹学-3对偶单纯形法

运筹学-3对偶单纯形法

1.对偶单纯形法的应用条件； 2.出基与进基的顺序； 3.如何求最小比值； 4.最优解、无可行解的判断。 作业：教材P76 T2.7
The End of Section 3
灵敏度分析 Exit
即对偶问题具有无
界解，由性质2a知ik 原问a题Lj 无可行解。aik
§2.3 对偶单纯形法 The Dual Simplex Method
Ch2 Dual Problem
2020年6月20日星期六 Page 9 of 9
本节利用对偶性质6：原问题的检验数与对偶问题的基本 解的对应关系，介绍了一种特殊线性规划的求解方法—对 偶单纯形法。
0
-4
-1
0
-1
— 1.6 — —
2
x2
0.4
0
1 -0.2 -0.4 0.2
x1
2.2
1
0
1.4 -0.2 -0.4
检验数 5.6
0
0 -1.8 -1.6 -0.2
最优解： x2=0.4 x1=2.2
Max z = -5.6
§2.3 对偶单纯形法 The Dual Simplex Method
Ch2 Dual Problem
【解】先将约束不等式化为等式，再两边同乘以（－1）， 得到
min z 2x1 3x2 4x3
x1 2x2 x3 x4 3
2x1 x2 3x3 x5 4
x
j
0,
j
1,2,
,5
用对偶单纯形法，迭代过程如下页或看演示(请启用宏)。
§2.3 对偶单纯形法 The Dual Simplex Method
问题中，λ≤j0分母aij<0，
j

第4章05-对偶单纯形法

第4章05-对偶单纯形法

第4章05对偶单纯形法同学们，大家好，今天我们来学习对偶单纯形法。

我们先看一下对偶单纯形法的原理。

前面讲单纯形法的时候，我们知道，一个基B 如果是最优基，那么它必须满足下面的三个条件：（1）B 是可逆的；（2）B -1b ≥0；（3）C−C B B -1A ≤0。

（1）B 可逆；（2）10B b -≥；（3）10B C C B A --≤我们在用单纯形法进行求解的时候，是先找到一个满足了前两个条件的可行基，然后在迭代过程中再逐步满足第三个条件，从而找到最优解。

而对偶单纯形法是先找到一个基满足第一个和第三个条件，然后在迭代过程中逐步满足第二条，最后也同样找到最优解。

我们把满足第一和第三个条件的基称为正则基。

也就是说，单纯形法是先找一个可行基，然后逐步迭代找到最优基；而对偶单纯形法是先找一个正则基，然后再逐步迭代找到最优基。

关于对偶单纯形法，我们还需要注意下面三点：首先，在判定最优解时，单纯形法中根据的是检验数行，而对偶单纯形法中根据的是检验数列，也就是单纯形表中右端项的列。

第二，对偶单纯形法是求解线性规划模型的另一种方法，而不要简单的理解为对偶单纯形法就是求解对偶线性规划模型。

第三，使用对偶单纯形法时，需要先找到正则基，但实际上找一个正则基并不容易，所以，对偶单纯形法往往不单独使用，而是与第五章的灵敏度分析配合使用。

下面我们通过例4-7来说明对偶单纯形法是如何操作的。

例4-71212121212min 233436st.22,0z x x x x x x x x x x =+--≤-⎧⎪--≤-⎪⎨--≤-⎪⎪≥⎩第一步，先把它化成标准型，写出约束矩阵A ，右端项b ，以及价值向量C ，如下所示。

1234512312412512345max 200033436st.22,,,,0z x x x x x x x x x x x x x x x x x x x =--++++-=⎧⎪+-=⎪⎨+-=⎪⎪≥⎩311004*********-⎛⎫ ⎪=- ⎪ ⎪-⎝⎭A ，362⎛⎫⎪= ⎪ ⎪⎝⎭b ，()21000=--C 第二步，找初始基。

第二节 对偶单纯形法

第二节 对偶单纯形法
1
二、对偶单纯形法求解原规划的主要步骤
1.建立初始对偶单纯形表 对应一个基本解, 1.建立初始对偶单纯形表,对应一个基本解,所 建立初始对偶单纯形表, 有检验数均非正, 有检验数均非正,转2； 2.若 ≥0,则得到最优解 停止;否则,若有b 2.若bi≥0,则得到最优解,停止;否则,若有bi<0 则得到最优解, 行的基变量为出基变量，并计算： 则选i行的基变量为出基变量，并计算： θ=min{σj/alj∣alj<0}=σk/σlk =min{σ <0}= }=σ 确定x 为进基变量。若有多个b <0， 确定xk为进基变量。若有多个bi<0，则选择最 小的进行分析。 小的进行分析。 3.以 为中心元素， 3.以alk为中心元素，按照与单纯形法类似的方 在表中进行迭代计算，返回第(2) (2)步 法，在表中进行迭代计算，返回第(2)步。
4
下面用对偶单纯形法求解： 下面用对偶单纯形法求解：
CB 0 0 0 -z 0 -2 0 比值 x3 x2 x5 -z -3 -2 0 -z 比值 x1 x2 x5 XB x3 x4 x5 b -3 -6 23 -4 -1 -3 -2 x2 -1 [-3] [-3 -2 0 x3 1 0 0 0 --1 0 0 0 ---3/5 4/5 9/5 -1/5 0 x4 0 1 0 0 ---1/3 -1/3 -1 -2/3 2 1/5 -3/5 - 8/5 -3/5 0 x5 0 0 1 0 --0 0 1 0 --0 0 1 0
三、对偶单纯形法的适用范围
适合于解如下形式的线性规划问题
在引入松弛变量化为标准型之后， 在引入松弛变量化为标准型之后，约束等式两侧 同乘同乘-1，能够立即得到检验数全部非正的原规划基本 可以直接建立初始对偶单纯形表进行求解， 解，可以直接建立初始对偶单纯形表进行求解，非常 方便。 方便。

运筹学对偶单纯形法

运筹学对偶单纯形法

对偶单纯形法特点 : (1) 简化计算： 不引入人工变量将线性规划化成标准型 , 构造
初始单纯形表 (初始解是非可行解 ), 只要检验数非负 (最优检 验数), 就可以进行基的转换； (2) 适于变量多于约束条件： 当变量少于约束方程的个数时， 可考虑变成对偶问题后，再用对偶单纯形法； (3) 局限性：多数问题很难找到检验数为负 (最优检验数 )的初 始可行解。但可用于灵敏度分析中简化计算。
(2) 先确定换出变量：若 min{(B-1b)i|(B-1b)i <0} = (B-1b)l
对应的基变量xl为换出变量。（实际上，可取任何一个取 负值的基变量作为换出变量。取最小的含义是尽快）
(3) 确定换入变量： 检查xl所在行的各系数alj(j = 1,2,…,n)。 若所有的 alj0,则无可行解，停止计算。


min



2 2
,

4
3



2 2
1，x1
为换入变量
主元素位置见表，迭代得下表
cj→ -2 -3 -4 0 0
CB XB b x1 x2 x3 x4 x5
0 x4 -1 0 [-5/2] 1/2 1 -1/2
-2 x1 2 1 -1/2 3/2 0 -1/2
cj -zj
注意： 1. 对偶单纯形法不是解对偶问题的单纯形法，而是应用 对偶原理求解原问题最优解的一种方法。当然，当求解得 到原问题的最优解的同时，也就得到对偶问题的最优解。
2.在具体计算中，不另外构造单纯形表格，而是在原始问 题的单纯形表格基础上进行对偶处理。
对偶单纯形法的计算步骤:
(1) 根据线性规划问题，列出初始单纯形表，检查b列的数 值，若都为非负，并且检验数都为非正，则已得到最优解。 停止计算；若b 列的数值至少还有一个负分量，检验数保 持非正，那么进行计算。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2.3 对偶单纯形法
一、什么是对偶单纯形法？
对偶单纯形法是应用对偶原理求解原始 线性规划的一种方法——在原始问题的单 纯形表格上进行对偶处理。
注意：不是解对偶问题的单纯形法！
二、对偶单纯形法的基本思想 1、对“单纯形法”求解过程认识的提升— —
从更高的层次理解单纯形法 初始可行基（对应一个初始基本可行解）
3 4
x1, x2 , x3, x4, x5 0
以此形式进行列表求解，满足对偶单纯形 法的基本条件，具体如下：
CB
XB
0
x4
0
x5
cj -2 -3 -4 0 0
xj b
x1 x2 x3 x4 x5
-3
-1 -2 -1 1 0
-4
-2 1 -3 0 1
-Z
0
-2 -3 -4 0 0
比
值 -2/-2 --- -4/-3 --- ---
2/5
11/5
-2 -3 -4 0 0 x1 x2 x3 x4 x5
0 1 -1/5 -2/5 1/5 1 0 7/5 -1/5 -2/5
cj-zj
0
0 0 -3/5 -8/5 -1/5
最优解: X*=（11/5，2/5, 0, 0, 0）T，
最优值: minW= -maxZ* = -[11/5×(-2)+2/5×(-3)]= 28/5
将三个等式约束两边分别乘以-1，然后
列表求解如下：
CB
XB
0
y3
0
y4
0
y5
-Z
比
cj yj b
-3 -9 0 y1 y2 y3
00 y4 y5
-2
-1 -1 1 0 0
-3
-1 -4 0 1 0-3-Fra bibliotek -7 0 0 1
0
-3 -9 0 0 0
值 -3/-1 -9/-1 --- --- ---
CB
CB
XB
0
x4
-2 x1
cj xj b
-1
2
-2 -3 -4 0 0 x1 x2 x3 x4 x5
0 -5/2 1/2 1 -1/2 1 -1/2 3/2 0 -1/2
cj-zj
比
0
0 -4 -1 0 -1
值 --- -4/-5/2 --- -1/-1/2
CB
XB
-3 x2
-2 x1
cj xj b
证明： C CBB-1A 0
(CB MCN ) CBB-1 (BMN) 0
(CB MCN ) (CBB-1BMCBB-1N) 0 (CB CBB-1BMCN CBB-1N) 0
CB CBB-1B 0 CN CBB-1N 0
N 0
单纯形法的求解过程就是：
在保持原始可行的前提下(b列保持≥0)，
通过逐步迭代实现对偶可行(检验数行≤0)。 2、 对偶单纯形法思想：
换个角度考虑LP求解过程：保持对偶可行 的前提下（检验数行保持≤0） ，通过逐步迭 代实现原始可行（b列≥0，从非可行解变成 可行解）。
对偶单纯形法的思想（图示）
始终满 足对偶 可行性
最优解 基本可行性 对偶可行性
保持对偶可行性 初始对偶可行解
XB
-3 y1
0
y4
0
y5
-Z
比
cj yj b
2 -1 -1
-3 -9 0 y1 y2 y3
1 1 -1 0 -3 -1 0 -6 -1
00 y4 y5
00 10 01
→迭代→另一个可行基（对应另一个基 本可行解），直至所有检验数≤0为止。
所有检验数≤0意味着
CN CB B1N 0 YA C ，
说明原始问题的最优基也是对偶问题的可行 基。换言之，当原始问题的基B既是原始可 行基又是对偶可行基时，B成为最优基。
定理2-5 B是线性规划的最优基的充要条件 是，B是可行基，同时也是对偶可行基。
保持为基本 可行解
原问题
初始基本 可行解
始终满足解 的可行性
三、对偶单纯形法的实施
1、使用条件： ①检验数全部≤0；
②解答列至少一个元素 < 0；
2、实施对偶单纯形法的基本原则：
在保持对偶可行的前提下进行基变换——每 一次迭代过程中取出基变量中的一个负分量 作为换出变量去替换某个非基变量(作为换入 变量),使原始问题的非可行解向可行解靠近。
素
a
' lk
为主元素。
若 值吗al'j？为0 ,要什计么算？最小比
按主元素进行换基迭代（旋转运算、枢 运算），将主元素变成1，主元列变成单位向 量，得到新的单纯形表。
循环以上步骤，直至求出最优解。
3、举例——用对偶单纯形法求解LP：
MinW 2x1 3x2 4x3
s.t.
2xx112xx223xx33
即
min i
( B 1b) i
( B 1b) i
0
(B1b)l ,则选xl出基，
相应的行为主元行。
然后确定换入变量——原则是：在保持对偶 可行的前提下，减少原始问题的不可行性。
如果
min j
c
j
al'j
z
j
al'j
0
ck zk
a
' lk
(最小比值原则),则选 xk 为换入变量 , 相应 的列为主元列 , 主元行和主元列交叉处的元
3 4
x1, x2, x3 0
化为标准型 →
MaxZ 2x1 3x2 4x3
s.t.
2xx112xx223xx33xx45
3 4
x1, x2, x3, x4, x5 0
将两个等式约束两边分别乘以-1，得
MaxZ 2x1 3x2 4x3
s.t.
2xx112xx223xx33xx45
3、计算步骤：
①建立初始单纯形表，计算检验数行。
解答列≥0——已得最优解； 检验数全部≤0 （非基变量检验数<0）
至少一个元素<0,转下步;
至少一个检验数>0
解答列≥0——原始单纯形法； 至少一个元素<0,另外处理；
基变换：
先 确 定 换 出 变 量 —— 解 答 列 中 的 负 元 素 （一般选最小的负元素）对应的基变量出基；
Max Z CX
LP原问题: AX b
s.t.
X
0
若B是A中的一个基
可行基
对偶可行基
B对应的解是基 本可行解，则B 是可行基
若单纯形乘子 Y CBB1 是对偶问题的可行解， 则B是对偶可行基
的CB可B行1 解是对偶问题
等价
检验数 N 0
YA C CBB-1A C C CBB-1A 0 N 0
4、举例——用对偶单纯形法求解LP：
MinW 3y1 9 y2
MaxZ 3y1 9 y2
y1 y2 2
s.t.
y1 y1
4y2 7 y2
3 3
化为
y1 y2 y3 2
标准型
→
s.t.
y1 y1
4 7
y2 y2
y4 y5
3 3
y1 0, y2 0
y1, , y5 0