对偶单纯形法

对偶单纯形法的原理和应用一、原理介绍对偶单纯形法是线性规划的一种求解方法，通过对原问题的对偶问题进行迭代求解，来达到求解原问题的目的。

下面详细介绍对偶单纯形法的原理。

1. 线性规划问题的对偶性在线性规划问题中，我们常常需要求解最小化或最大化线性目标函数的问题，同时满足一系列线性约束条件。

对于这样的问题，可以通过定义对偶问题来求解。

2. 对偶问题的定义对于原问题的最小化形式，可以定义对偶问题的最大化形式。

对于原问题的最大化形式，可以定义对偶问题的最小化形式。

对偶问题和原问题之间具有很强的对称性。

3. 对偶单纯形法的基本思想对偶单纯形法的基本思想是通过迭代求解对偶问题来达到求解原问题的目的。

在每一次迭代中，首先确定最优解是否已经找到，如果找到最优解，则结束算法；否则，确定要改进的变量，通过计算改变最变量之前对应的对偶变量的值，然后再进行下一次迭代。

二、应用场景对偶单纯形法在实际应用中有着广泛的应用场景。

下面列举几个典型的应用场景。

1. 生产计划问题在生产计划问题中，常常需要确定各个生产线的产量，以最小化总成本或最大化总利润。

对偶单纯形法可以应用于该问题的求解，通过定义对偶问题，并通过迭代求解对偶问题，来确定生产线的产量。

2. 项目调度问题在项目调度问题中，需要确定各个项目的开始时间和结束时间，以最小化总工期或最大化资源利用率。

对偶单纯形法可以应用于该问题的求解，通过定义对偶问题，并通过迭代求解对偶问题，来确定项目的调度方案。

3. 运输问题在运输问题中，需要确定各个供应商到各个销售点的运输量，以最小化总运输成本。

对偶单纯形法可以应用于该问题的求解，通过定义对偶问题，并通过迭代求解对偶问题，来确定每个供应商和销售点的运输量。

4. 资源分配问题在资源分配问题中，需要确定各个资源的分配比例，以最大化总效益或最小化总成本。

对偶单纯形法可以应用于该问题的求解，通过定义对偶问题，并通过迭代求解对偶问题，来确定资源的分配比例。

对偶单纯形法的条件
首先，对偶单纯形法的条件包括：
1. 对偶可行性条件，对偶单纯形法要求原始问题和对偶问题都是可行的。

也就是说，原始问题的约束条件和对偶问题的变量非负条件都必须满足。

2. 对偶非退化条件，这个条件要求对偶单纯形表中的对偶变量都是非负的，且对偶问题的最优解是非退化的。

3. 对偶互补松弛条件，这个条件指的是原始问题的最优解和对偶问题的最优解之间存在一种互补关系，即原始问题的最优解和对偶问题的最优解必须满足一组互补松弛条件。

其次，对偶单纯形法的条件还涉及到对偶单纯形表的构建和迭代计算的条件：
1. 对偶单纯形表的构建需要满足对偶问题的约束条件和非负条件，通过构建对偶单纯形表，可以进行对偶单纯形法的迭代计算。

2. 对偶单纯形法的迭代计算需要满足一定的迭代规则和条件，
包括选择合适的进入变量和离开变量，进行主元素的换入换出操作，更新对偶单纯形表等操作。

最后，对偶单纯形法的条件还包括了对原始问题和对偶问题的
理解和转化能力：
1. 需要理解原始问题和对偶问题之间的对偶关系，以及如何通
过对偶问题来求解原始问题的最优解。

2. 需要具备将原始问题转化为对偶问题的能力，以及对对偶问
题的理解和求解能力。

总的来说，对偶单纯形法的条件涉及到对原始问题和对偶问题
的理解、对偶单纯形表的构建和迭代计算条件，以及对偶问题的可
行性、非退化性和互补松弛条件的满足。

这些条件是对偶单纯形法
顺利求解线性规划问题的基础，需要严格满足和理解。

介绍对偶单纯型算法
对偶单纯形法是一种求解线性规划问题的算法。

它基于线性规划问题的对偶理论，从对偶可行性出发，通过迭代搜索，逐步找出原始问题的最优解。

在具体操作上，对偶单纯形法首先需要设定一个初始基和对应的最优解。

然后，它会根据对偶问题的约束条件进行迭代，每次迭代都会根据一定规则（如“进基”和“出基”规则）更新基和对应的最优解。

当无法找到能使目标函数值更优的可行解时，算法结束，此时得到的解即为原始问题的最优解。

对偶单纯形法具有一些优点。

例如，它可以处理一些不可行或无界的情况，这些情况可能会让原始单纯形法束手无策。

此外，对偶单纯形法还可以提供对偶问题的信息，这些信息可能有助于理解原始问题的性质。

然而，对偶单纯形法也有一些缺点。

例如，它需要处理的是对偶问题而非原始问题，这可能会导致一些计算上的复杂性。

此外，虽然对偶单纯形法可以找到最优解，但它不能提供任何关于解的可行性和最优性的证明。

总的来说，对偶单纯形法是一种有效的求解线性规划问题的算法，但使用时需要注意其可能存在的局限性。

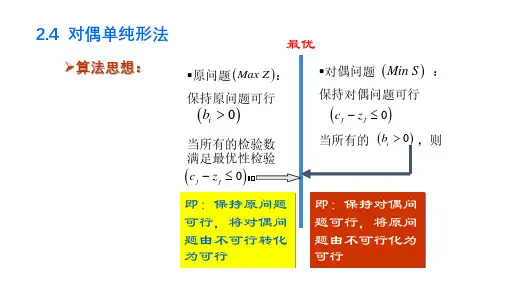
对偶单纯形法一. 对偶单纯形的思想：考虑线性规划问题..min ≥= x bAx t s xc T基本思想：从线性规划问题的一个基本解出发，迭代过程中 不要求基本解满足可行性（即允许基本解中存在负分量），但要求始终保持基本解的检验数小于等于0（即始终保持T T B B c )(1−为其对偶线性规划问题的可行解，逐步减少基本解中的负分量的个数，直至基本解中没有负分量为止就得到了问题的最优解。

这种迭代方法即为对偶单纯形法。

注：对偶单纯形法是根据对偶原理求解线性规划问题的 另一种单纯形法。

对偶单纯形法的迭代依然是以主元lk b 为主元的转轴运算，但它也有自己的特点。

它是先确定离开基的变量，即先确定l x ，然后确定进入基的变量，即确定k x 。

1. 最优性的判别已知线性规划问题的一个基矩阵B 及与它对应的基本 解⎟⎟⎠⎞⎜⎜⎝⎛0B x ，且此基本解的所有判别数0≤。

若01≥=−b B x B ，则所得到的基本解为最优解.(3) 以lk b 为主元进行转轴运算，返回（1）。

例1 用对偶单纯形法求解线性规划问题,, 12 423 32 ..3min 32132121321321≥≥−+≥+≥++++=x x x x x x x x x x x t s x x x f解：引入松弛变量654,,x x x ，将给定的线性规划问题化为标准形式,,,,, 12 423 32 ..3min 65432163215214321321≥=−−+=−+=−++++=x x x x x x x x x x x x x x x x x t s x x x f为了得到对偶问题的一个可行解，把每个约束方程两端乘以（-1），变换后的系数置于单纯形表：。

对偶单纯形法bland法则
偶单纯形法(Duality Simplex Algorithm)是求解线性优化问题的一种常见方法。

这种方法的核心思想是基于线性规划的对偶性的。

它的基础是著名的双重模型(dual problem)，即由原始线性规划问题派生出的等价的对偶线性规划问题。

偶单纯形法是将求解整数规划问题的配套技术，是一种基于可变缩减实现系统设计的启发式方法。

原始线性规划问题通过变量的解除转化为一个对偶的新的线性规划问题。

偶单纯形法比较适用于不约束的线性优化问题，也可以被应用到更加复杂的约束条件下的求解问题。

Bland法则是偶单纯形法的一种变体，该法则提出要在每一步中都选择最“可能”基本变量进行变换，可能意味着从潜在可行性基变量中选择120英寸可行松弛性单纯形变量。

该法则是线性优化中比较重要的最小化技术，可用于执行最优化准则，检查问题的最优解，并在找到最优解前止血处理的可行解。

偶单纯形法与Bland法则的中心思想在于解决线性规划问题，它们最大的优势在于能够解决问题更加迅速和有效，同时在系统推导出算法时，可以更容易理解和实现。

偶单纯形法Bland法则是常用的算法之一，它将精确解决线性优化问题，可以在短时间内找到可行解，可以开发出一类求解工具，帮助企业和机构解决线性规划问题，以获得自己理想的最优解。

对偶单纯形法的条件对偶单纯形法是线性规划中一种重要的求解方法，主要用于解决线性规划问题的对偶问题。

它通过对原问题进行转化和运算，求解出对偶问题的最优解，从而得到原问题的最优解。

对偶单纯形法是基于单纯形法的扩展，具有更广泛的适用性和更高效的求解效果。

对于使用对偶单纯形法求解线性规划问题，需要满足以下条件：1. 原问题必须是标准形式的线性规划问题：目标函数为最小化形式，约束条件为等式形式，并且所有变量的取值范围为非负数。

2. 原问题必须存在可行基本解：可行基本解是指满足所有约束条件的解，可以通过单纯形法或其他方法求得。

3. 原问题的最优解必须有限：即原问题存在最优解，不是无界的。

在满足以上条件的基础上，使用对偶单纯形法求解线性规划问题的步骤如下：步骤一：建立对偶问题根据原问题的约束条件和目标函数，建立对偶问题的目标函数和约束条件。

对偶问题的目标函数为原问题的约束条件的系数构成的向量与对偶变量的乘积之和，约束条件为原问题的目标函数的系数构成的向量与对偶变量之和等于对偶约束条件的系数构成的向量。

步骤二：初始化给定初始对偶变量的取值，通常取为0，然后计算初始对偶解。

步骤三：判断最优性根据当前对偶解，判断原问题的最优性。

如果原问题的最优性条件满足，则停止计算，得到最优解；否则，进行下一步。

步骤四：选择换入变量根据当前对偶解，选择换入变量。

具体方法是在对偶约束条件中，选择不满足约束条件且对偶变量目标函数系数最小的变量作为换入变量。

步骤五：选择换出变量根据换入变量，选择换出变量。

具体方法是在换入变量所对应的约束条件中，选择满足约束条件且使对偶解最小的变量作为换出变量。

步骤六：更新对偶解根据换入、换出变量，更新对偶解。

具体方法是用换入变量替换对应的换出变量，计算新的对偶解。

重复步骤三到六，直到原问题的最优性条件满足为止。

最终得到原问题的最优解和对偶问题的最优解。

对偶单纯形法的优点在于它能够通过解决对偶问题来求解原问题，从而减少了计算量，提高了求解效率。