平曲线的详细测设—切线支距法

切线支距法
（最新版）
目录
1.切线支距法的定义和原理
2.切线支距法的应用
3.切线支距法的优点和局限性
正文
切线支距法是一种用于测量物体长度的方法，主要通过测量物体切线与支点之间的距离来计算物体的长度。

这种方法的原理基于几何学中的切线定理，即在平面上，从一个点到一条直线的切线与该点到直线的垂线段之间的距离相等。

切线支距法在实际应用中具有广泛的应用。

例如，在工程测量中，常常需要测量建筑物或者道路的长度，这时候切线支距法就可以派上用场。

此外，切线支距法也可以用于测量物体的高度、宽度等尺寸。

切线支距法的优点在于操作简便，只需要测量切线与支点之间的距离，再根据切线定理计算出物体的长度即可。

而且，切线支距法的测量结果相对准确，只要操作得当，就能够获得较为精确的长度测量结果。

然而，切线支距法也存在一些局限性。

首先，切线支距法只适用于平面上的测量，对于立体物体的测量则无法使用。

其次，切线支距法的测量结果受到测量仪器精度的影响，如果仪器精度不高，那么测量结果也会存在偏差。

总的来说，切线支距法是一种简单而实用的测量方法，适用于各种平面测量场景。

第1页共1页。

473.4.5 切线支距法敷设曲线计算方法①用切线支距法敷设回旋线公式：式中：l ——回旋线上任意点m 至缓和曲线终点的弧长（m ）。

②切线支距法敷设带有回旋线的圆曲线公式：x = q + R sin ϕm (m) y = p + R (1 - cos ϕm ) (m)式中： l m ——圆曲线上任意点m 至缓和曲线起点的弧长（δ——l m 所对应的圆心角（rad ）例题：已知平原区某二级公路有一弯道，JD=K2+536.48，偏角α右=15°28′30″，半径R=600m ，缓和曲线长度Ls=70m 。

要求：（1）计算曲线主点里程桩号；（2）计算曲线上每隔25m 整桩号切线支距值。

解：（1）曲线要素计算：48J=2T-L=2×116.565-232.054=1.077（2）主点里程桩号计算：以交点里程桩号为起算点：JD = K2+536.48ZH = JD – T =K2+536.48 - 116.565 = K2+419.915HY = ZH + Ls = K2+419.915 +70 = K2+489.915QZ = ZH + L/2= K2+419.915+232.054/2 =K2+535.942HZ = ZH + L = K2+419.915 +232.054 =K2+651.969YH = HZ – Ls = K2+651.97 –70=K2+581.969（3）计算切线支距值：①缓和曲线段：ZH=K2+419.915②圆曲线段：HY=K2+489.915 ，YH =K2+581.969LCZ=K2+500，l m= 2500 - 2489.915 = 10.085=34.996+250sin4.3053=80.038(m)x = q + Rsinϕmy = p + R(1-cosϕ) = 0.34+250（1-cos4.3053）=2.033(m)m③计算曲线上每隔25m整桩号的切线支距值：列表计算曲线25m整桩号：ZH= K2+419.915，K2+425，K2+450，K2+475，K2+500 …49。

测量员必须掌握的曲线种类和测设方法曲线测设是将把图纸上的曲线标定在地面上，供施工使用。

是施工测量中常用的方法，也是测量当中一项重要的技术。

大家是否知道曲线有哪些种类，不同种类又有哪些方法测设曲线呢？小编接下来就给大家讲解一下曲线的相关知识。

一、曲线种类：曲线分为了平面曲线和竖曲线。

（一）平面曲线：1、圆弧曲线：具有一定半径的曲线称为圆弧曲线，圆弧曲线又包含单曲线、复曲线、反向曲线和回头曲线等。

2、缓和曲线：连接直线和曲线的过渡曲线称为缓和曲线，缓和曲线的半径半径由无穷大逐渐变化为圆弧曲线半径。

（二）竖曲线：连接两个相邻坡度线的凸形和凸形曲线称为竖曲线，目的是为了缓和坡度在变坡点的急剧变化。

二、曲线测设方法：（一）圆曲线测设1.切线支距法以圆曲线的起点或终点为坐标原点，以圆曲线的切线为X轴，过原点的半径方向为Y轴建上各点坐标X、Y设置曲线。

2.偏角法：以圆曲线起点或终点至曲线任一待定点P的弦线与切线之间的弦切角和弦长来确定P点的位置偏角法是一种灵活性比较大，适用性较强的方法。

但存在测点误差累积的问题，宜从起终点向中点或中点向起终点测设曲线。

切线支距法适用于开阔遍野的地方，测量简单、方便。

但精度较低。

除以上方法还根据细致的分类，有更多的测量方法（二）竖曲线测设1. 建立抛物线的竖曲线方程式的建立（1）抛物线起点为S，终点为T，设置起点坐标S（0,YS），终点坐标（XT,YT）（2）建立两条分别过S和T两点的切线，两切线交点为P（3）求ST中点的坐标 Q（XQ,YQ）和切点P的坐标（XP,YP）并求出中点和切点连线中与抛物线的交点R求出R（XR,YR）（4）最后求坐标系的旋转角α和S、R、T在X’OY’的坐标这次关于曲线测设的方法就讲解到这里啦，如果还有对曲线测设有什么问题，可以咨询东英时代，我们会一一为大家解答，如果对仪器操作不熟练，建议大家来东英时代培训学校进行实战培训。

切线支距法
切线支距法是一种用于计算曲线弯曲半径的方法，它基于曲线上某一点的切线长度和曲率半径的关系。

在切线支距法中，首先要找到曲线上某一点的切线方向，这可以通过计算曲线在该点处的导数来实现。

一旦知道了切线方向，就可以将其延长，直到它与曲线相切。

此时，可以通过计算切线长度和曲线弯曲程度来确定曲线的弯曲半径。

具体来说，假设曲线上某一点处，切线向量为t，法向量为n，曲率半径为r。

则可以通过以下公式计算切线支距d：d=r*sin(θ)，其中，θ是切线向量和法向量之间的夹角。

切线支距法可以用于计算任意曲线的弯曲半径，包括圆弧、椭圆等。

在工程和科学领域中得到广泛应用，例如可以用于计算道路和铁路的弯曲半径，以确保车辆能够安全通过。

切线支距法
（原创版）
目录
1.切线支距法的定义
2.切线支距法的应用
3.切线支距法的优缺点
4.切线支距法的发展前景
正文
切线支距法是一种在数学和物理学中经常使用的求解问题的方法。

切线支距法，顾名思义，是通过作图找到切线，然后通过切线的长度来求解问题的方法。

切线支距法最常见的应用是在力学中，特别是在静力学中。

例如，当一个物体放在一个斜面上时，我们可以通过作图找到斜面上物体所受到的支持力的切线，然后通过切线的长度来求解支持力的大小。

这种方法不仅可以求解支持力的大小，还可以求解支持力的方向，因此在实际问题中非常有用。

切线支距法的优点在于简单易懂，操作方便，而且结果准确。

只要作图准确，通过切线支距法求解出来的结果就可以直接应用到实际问题中。

但是，切线支距法也有其缺点，那就是它只适用于一些简单的问题，对于一些复杂的问题，切线支距法可能无法准确求解。

随着科学技术的发展，切线支距法的应用范围也在不断扩大。

现在，切线支距法不仅在数学和物理学中使用，还在工程学、地理学等学科中得到应用。

可以预见，随着科学技术的不断发展，切线支距法的应用前景将更加广阔。

总的来说，切线支距法是一种简单有效的求解问题的方法，它不仅可
以帮助我们解决实际问题，还可以帮助我们更好地理解科学原理。

切线支距法原理范文切线支距法（也称为平切法、切带法或纸带法）是一种测量地球上任意两点之间的直线距离的方法。

该方法基于地球的曲率，利用切线与球面的接触点之间的线段长度来计算两点之间的距离。

下面将详细介绍切线支距法的原理和计算过程。

1.地球的曲率地球是一个近似为椭球体的3D物体，因此不能简单地通过平面几何方法来计算其直线距离。

由于地球的曲率，两点之间的距离不再是直线，而是沿着地球表面的一条曲线。

因此，为了测量地球上两点之间的距离，需要使用球面几何学的原理。

2.切线接触点3.切线支距的计算一旦找到了切线与球面的接触点，即与起点和终点最近的点，便可以通过计算切线与球面接触点之间的线段长度来测量两点之间的距离。

切线支距也被称为切线长度或切带长度。

4.切线支距的计算公式在切线支距法中，使用下面的公式来计算切带长度：切带长度 = 地表弧长× cosA其中，地表弧长表示起点和终点之间的地表曲线距离，而A表示两点之间的小弧度。

在计算过程中，通常将角度转化为弧度来进行计算。

5.实际应用6.优点和限制-较高的精度：该方法可以提供比利用经纬度计算距离更精确的结果。

-简单易用：使用简单的公式和计算方法，不需要复杂的数学操作。

-适用广泛：可应用于各种地理环境和大范围的距离测量。

然而，切线支距法也有一些限制：-局限于球面：该方法仅适用于地球这样的近似球体，对于不规则的地形和地球模型可能不适用。

-相对复杂的计算：虽然计算方法相对简单，但需要进行一些角度和弧度的转换。

-潜在的误差：由于地球表面并非完全光滑和规则，切线支距法可能会引入一些误差。

综上所述，切线支距法可以提供精确的直线测距结果，适用于各个领域的距离测量。

但在实际使用中，需要注意其局限性和潜在的误差，结合其他测量方法来确保结果的准确性。

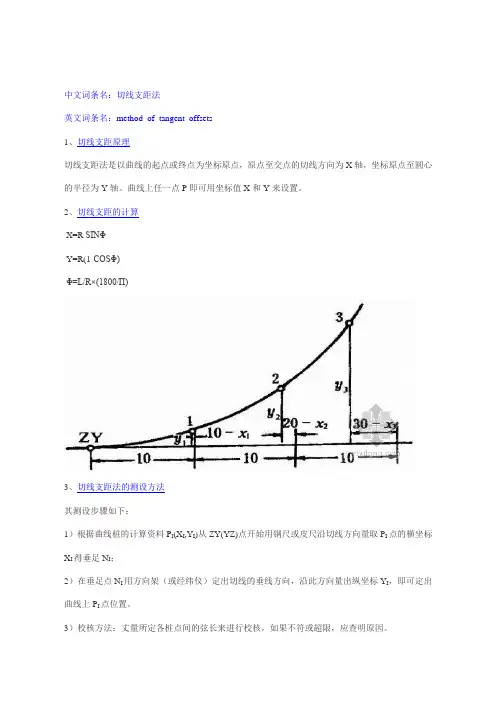
中文词条名：切线支距法英文词条名：method of tangent offsets1、切线支距原理切线支距法是以曲线的起点或终点为坐标原点，原点至交点的切线方向为X轴，坐标原点至圆心的半径为Y 轴。

曲线上任一点P即可用坐标值X和Y来设置。

2、切线支距的计算X=R SINΦY=R(1-COSΦ)Φ=L/R×(1800/Π)3、切线支距法的测设方法其测设步骤如下：1）根据曲线桩的计算资料P I(X I,Y I)从ZY(YZ)点开始用钢尺或皮尺沿切线方向量取P I点的横坐标X I得垂足N I；2）在垂足点N I用方向架（或经纬仪）定出切线的垂线方向，沿此方向量出纵坐标Y I，即可定出曲线上P I点位置。

3）校核方法：丈量所定各桩点间的弦长来进行校核，如果不符或超限，应查明原因。

切线支距法简单，各曲线点相互独立，无测量误差累积。

但由于安置仪器次数多，速度较慢，同时检核条件较少，故一般适用于半径较大、Y值较小的平坦地区曲线测设。

如果您认为本条内容需要改进，请点击这里编辑修改第一条缓和曲线部分：X=L- L 5/（40×R2×L 02）Y=L3/(6×R×L 0)这是以ZH点为坐标原点测设到YH点的计算公式圆曲线部分X=R×sina+mY=R×(1-cosa)+pa=( L i- L)×1800/(R×π)+β0m = L 0/2- L 03/(240×R2)P= L 02/(24×R)- L 04/(2688×R3)δ0= L 0×1800/(6×R×π)β0= L 0×1800/(2×R×π)T=（R+P）×tg（a/2）+mL= R×（a-2β0）×π/1800+2L 0切线角的计算β= L2×1800/（2×R×L0 ×π）缓和切线角的弧度计算：β= L2/（2×R×L0）圆曲线切线角的弧度计算：a=( L i- L 0) /R+ L 0/(2×R)上式中：m表示切垂距。

公路工程平曲线测量方法优选蒋李陵;闫志;赵忠梅【摘要】公路建设时有经过高山、峡谷、河流、森林等地形条件,公路弯道经过此类障碍时,单一平曲线放样方法往往会出现不通视、虚交点、双交点等特殊情况.介绍了目前常用的4种平曲线测量放样方法的测量原理,分析了4种测量放样方法的现场应用情况.结果表明,通过多种测量方法的综合应用,可以有效地解决测设过程遇障碍的问题,置镜交点的极坐标放样法、长弦偏角法等各点独立测设的方法精度准确,测设效率高.【期刊名称】《石油工业技术监督》【年(卷),期】2016(032)009【总页数】3页(P56-58)【关键词】公路工程;测量方法;测量原理;平曲线【作者】蒋李陵;闫志;赵忠梅【作者单位】中国石油吐哈油田分公司监督中心新疆鄯善838200;中国石油西部钻探吐哈钻井公司新疆鄯善838202;中国石油吐哈油田分公司监督中心新疆鄯善838200【正文语种】中文公路施工，测量先行。

测量是施工的基础与先导，是设计意图的最直接体现，测量的准确性关系到整个工程的成败。

新疆幅员辽阔，地貌复杂，公路建设跨越或穿越高山、峡谷、河流、森林等地形条件的情况比较常见。

公路平曲线经过此类障碍时，由于单一平曲线放样方法出现不通视、虚交点、双交点等特殊情况，造成测量困难，需要综合采用不同的测量方法。

目前常用的平曲线测量放样方法有切线支距法、偏角法、极坐标法和长弦偏角法等，对4种平曲线测量方法的适用条件、效率、精度等方面进行探讨。

1.1 偏角法采用偏角法［1］详细测设曲线，如图1所示，需要分别置镜于四大主点（直缓点、缓圆点、圆缓点、缓直点）之一，相对于置镜点处曲线的切线方向，正拨或反拨待测点到置镜点与切线方向的偏角，同时相对于已测定点位丈量距离，视线定向与钢尺量距相交即可测设出曲线上的待测点。

1.2 切线支距法切线支距法测设原理如图2所示，根据放样元素公式推算曲线上各点的纵横坐标，然后根据坐标对曲线上的点进行量测定位的一种测量方法［2］。

第十二章 平曲线测设公路路线平曲线测设是公路工程测量的重要组成部分。

平曲线基本形式有：圆曲线、缓和曲线、复曲线和回头曲线等。

本章主要介绍平曲线的常规测设原理与方法，以及单曲线遇障碍的测设。

通过本章的学习，学生应能够：会用切线支距法和偏角法详细测设园曲线；理解遇障碍时曲线的测设方法；描述缓和曲线；能用切线支距法和偏角法测设带有缓和曲线段的园曲线；第一节 圆曲线主点测设在路线平曲线测设中，圆曲线是路线平曲线的基本组成部分，且单圆曲线是最常见的曲线形式。

圆曲线的测设工作一般分两步进行，先定出曲线上起控制作用的点，称为曲线的主点测设，然后在主点基础上进行加密，定出曲线上的其它各点，完整地标定出圆曲线的位置，这项工作称为曲线的详细测设。

一、圆曲线测设元素的计算在图12-1中：图 12-1P 点——公路路线测量中所测定的交点JD 位置；α——路线转角；R ——圆曲线半径；A 点和B 点——直线与圆曲线的切点，即圆曲线的起点ZY 和终点YZ ； M 点——分角线与圆曲线的相交点，即圆曲线的中点QZ ； T ——圆曲线的切线长； L ——圆曲线的曲线长； E ——交点JD 至圆曲线中点M 的距离，称为外距。

根据图中的几何关系，单圆曲线元素按下列公式计算：切线长： 2tanαR T =曲线长： R L απ︒=180 （12-1）外距： )12(sec-=αR E另外，为了计算里程和校核，还应计算切曲差（超距），即两切线长与曲线长的差值。

切曲差（超距） D=2T-L二、圆曲线的主点测设单圆曲线有三个主点，即曲线起点（ZY ）、曲线中点（QZ ）和曲线终点（YZ ）。

它们是确定圆曲线位置的主要点位。

在其点位上的桩称为主点桩，是圆曲线测设的重要桩志。

1．主点里程桩号的计算在中线测时中，路线交点（JD ）的里程桩号是实际丈量的，而曲线主点的里程桩号是根据交点的里程桩号推算而得的。

其计算步骤如下：交点 JD 里程 -) T 圆曲线起点 ZY 里程 +) L 圆曲线终点 YZ 里程 -) L /2 圆曲线中点 QZ 里程 +) D /2 校核 JD 里程2．主点的测设 如图12-1所示，自路线交点JD 分别沿后视方向和前视方向量取切线长T ，即得曲线起点ZY 和曲线终点YZ 的桩位。

切线支距法
摘要：
1.切线支距法简介
2.切线支距法的应用
3.切线支距法在实际问题中的应用案例
4.总结
正文：
切线支距法是一种在数学和物理学中常用的方法，它可以用来解决曲线运动、力学和电磁学等领域的问题。

这种方法利用切线的概念，通过计算切线与坐标轴的交点，可以确定曲线运动物体的位置和速度。

切线支距法的应用十分广泛。

在物理学中，它可以用来解决平抛运动、圆周运动等问题。

在数学中，它可以用来解决微积分、线性代数等问题。

此外，在计算机图形学、工程学和天文学等领域，切线支距法也发挥着重要作用。

以平抛运动为例，假设一个物体在水平方向上以初速度v0投掷，竖直方向上受到重力加速度g的作用。

我们可以通过切线支距法来计算物体在空中的运动轨迹。

首先，我们需要计算物体在水平方向和竖直方向上的速度。

水平方向上的速度始终保持不变，即v0。

竖直方向上的速度可以通过公式vy = gt来计算，其中t为时间。

接下来，我们需要计算物体在各个时刻的切线方程。

根据初速度和加速度，我们可以得到物体在时刻t的切线方程为：y - y0 = v0t - 0.5gt^2。

与x 轴相交的点即为物体在时刻t的水平位置。

通过计算这个交点，我们可以得到
物体在空中的运动轨迹。

在实际问题中，切线支距法的应用可以帮助我们更好地理解物体的运动规律，从而为实际问题提供解决方案。

例如，在导弹轨迹规划中，通过使用切线支距法，可以预测导弹的飞行轨迹，从而提高导弹的命中精度。

总之，切线支距法是一种在多个领域具有重要应用价值的数学方法。

切线支距法计算公式
切线支距法是一种常用的测量方法，用于计算两个平行线之间的距离。

该方法通过测量两个平行线上的任意一点到另一个平行线上的切线的长度来确定距离。

切线支距法的计算公式如下：
切线支距 = 切线长度× (1/切线斜率)
其中，切线长度是从任意一点到切线的长度，切线斜率是切线与水平方向的夹角的正切值。

在实际应用中，切线支距法经常用于测量建筑物之间的间距、道路宽度等。

下面以测量建筑物之间的间距为例进行详细说明。

首先，选择两个平行线上的任意一点，分别为点A和点B。

然后，通过测量从点A和点B到另一个平行线上的切线的长度来确定距离。

假设从点A到另一个平行线上的切线的长度为L1，从点B到另一个平行线上的切线的长度为L2。

另外，假设点A的切线斜率为k1，点B的切线斜率为k2。

根据切线支距法的计算公式，可以得到：
切线支距 = L1 × (1/k1) = L2 × (1/k2)
通过测量L1和L2，并计算k1和k2的值，可以求得两个平行线之间的距离。

需要注意的是，为了保证测量结果的准确性，需要选择切线点A和点B时，尽量使切线斜率k1和k2的值较大，以减小测量误差。

总结起来，切线支距法是一种通过测量切线长度和切线斜率来计算两个平行线之间距离的方法。

它在测量建筑物间距、道路宽度等应用中具有广泛的实用性。

利用切线支距法测设非对称型平曲线非对称型平曲线是一种自然地形或人工地形，它不具有对称性，而是沿着一条曲线有较大的变化。

在建设道路、管道、铁路、水利等工程时，需要对非对称型平曲线进行测量。

本文将讨论利用切线支距法测设非对称型平曲线的方法、步骤及注意事项。

一、切线支距法测设非对称型平曲线的原理切线支距法是利用实测数据计算出各点处曲线的切线倾角和弯矩，最后推算出各点的高程值。

该方法将曲线近似为若干条等距离线段的连续整体，将曲线上任意一点处的曲率半径表示为其斜率之倒数。

根据平面几何的相关公式求出曲线上任意一点处的切线倾角。

最终利用解析公式把曲线的横截面轮廓用多项式函数来表示，得到曲线的高程等参数。

二、切线支距法测设非对称型平曲线的步骤1. 建立原始数据。

依据现场实测数据，建立起“距离-X”、“到中线的偏差-Y”，及该点对称轴的坡度变化值的“曲率-C”三个序列。

2. 计算弯矩值。

由原始数据中的距离和偏差，利用微积分计算得到当前段弯矩值。

3. 拟合函数。

根据得到的曲率和弯矩值，采用最小二乘法，建立各个点的拟合函数，进行各点的弯矩值的计算。

4. 计算切线倾角。

如果该段曲线形态已知，则可以根据已知的形态参数计算出切线角。

如果曲线形态未知，则需要根据拟合函数计算出弯矩值以进行切线角计算。

5. 推算高程值。

最后根据多项式式提取能得出每个点的高程值。

三、切线支距法测设非对称型平曲线的注意事项1. 周围环境：在测设非对称型平曲线时，需要注意周围环境是否干扰测量结果，应选择平坦的场地并及时清除障碍。

2. 测量仪器：选择准确、精确、稳定、易于操作的测量仪器进行测量，保证数据精确性和可靠性。

3. 测量过程：在测量过程中必须采用严格的步骤，确保各项数据的准确性和一致性。

4. 数据处理：数据处理要准确、快捷、简便，并采取科学、合理的处理方法，以保证数据的可靠性，避免人为错误的出现。

5. 算法应用：测量数据按照步骤进行处理，根据各种公式和计算方法进行算法应用，以便得到正确的结果。

在测量中，将平面曲线放样在实地上采用的方法一般有两种：弦线偏角法和切线支距法。

弦线偏角法
弦线偏角法操作：
1.将经纬仪架设在直线与曲线的起点上（ZY）
2.将经纬仪后视曲线的终点（YZ），读数为0,固定。

3.确定曲线上放样的第一点X，计算X与Y之间的偏角A。

4.将经纬仪镜头转到A，定位，这一就是当前曲线从起点到
X长度的实地点。

5.如此类推。

切线支距法
切线支距法又称直角坐标法，是以曲线的起点ZY或终点YZ 为坐标原点，以切线为 X 轴，经过原点的半径为 Y 轴，按曲线上各点坐标x、y设置曲线上各点的位置。

如图，设Pi为曲线上欲测设的点位，该点至ZY点或YZ 点的弧长为li，φi为li所对的圆心角，R为圆曲线半径，则Pi的坐标可按下式计算：
xi=Rsinφi
yi=R(1-cosφi)=xtan(φi/2)
式中：
φi=li/R(rad)。