切线支距法计算综合曲线

实习四 圆曲线详细测设——切线支距法一、实习目的及要求1. 学会用切线支距法详细测设圆曲线。

2. 掌握切线支距法测设数据的计算及测设过程。

二、仪器设备与工具1. 由仪器室借领：经纬仪1台、皮尺1把、小目标架3根、测钎若干个、方向架1个、记录板1块。

2. 自备：计算器、铅笔、小刀、记录计算用纸。

三、实习方法与步骤1．切线支距法原理：切线支距法是以曲线起点YZ 或终点ZY 为坐标原点，以切线为X 轴，以过原点的半径为Y 轴，根据曲线上各点的坐标（X ，Y ）进行测设，故又称直角坐标法。

如图9-1所示，设P 1、P 2…为曲线上的待测点，l i 为它们的桩距（弧长），其所对的圆心角为i ϕ，由图可以看出测设元素可由下式计算 ：式中：2. 测设方法（1）在实习前首先按照本次实习所给的数据计算出所需测设数据。

（2）根据所算出的圆曲线主点里程测设圆曲线主点。

（3）将经纬仪置于圆曲线起点(或终点)，标定出切线方向，也可以用花杆标定切线方向。

（4）根据各里程桩点的横坐标用皮尺从曲线起点(或终点)沿切线方向量取x 1、x 2、x 3……，得各点垂足，并用测钎标记之，如图4-1所示。

（5）在各垂足点用方向架标定垂线，并沿此垂线方向分别量出y 1、y 2、y 3……，即定出曲线上P 1、P 2、P 3……各桩点，并用测钎标记其位置。

sin (1cos )x R y R ϕϕ==-180l R ϕπ︒=⋅图4-1 切线支距法测设原理（6）从曲线的起(终)点分别向曲线中点测设，测设完毕后，用丈量所定各点间弦长来校核其位置是否正确。

也可用弦线偏距法进行校核。

五、实习数据已知：圆曲线的半径R =100 m，JD2的里程为K4 +296.67，桩距l =10 m，按切线支距整桩距法设桩，试计算各桩点的坐标(x，y)，并详细测设此圆曲线（转角视实习场地现场测定）。

切线支距法详细测设圆曲线数据记录表日期：班级：组别：观测者：记录者：交点号交点里程转角观测结果盘位目标水平度盘读数半测回右角值右角转角盘左盘右曲线元素R(半径)= T(切线长) =E(外距)=α (转角) = L(曲线长)= D(切曲差)=主点桩号ZY 桩号： QZ 桩号： YZ桩号:各中桩的测设数据桩号曲线长x y 备注略图：计算：检核：。

缓和曲线的切线支距法和偏角法的计算公式和测设方法理解线路勘测设计阶段的主要测量工作（初测控制测量、带状地形图测绘、中线测设和纵横断面测量）；掌握路线交点、转点、转角、里程桩的概念和测设方法；掌握圆曲线的要素计算和主点测设方法；掌握圆曲线的切线支距法和偏角法的计算公式和测设方法；了解虚交的概念和处理方法；掌握缓和曲线的要素计算和主点测设方法；理解缓和曲线的切线支距法和偏角法的计算公式和测设方法；掌握路线纵断面的基平、中平测量和横断面测量方；了解全站仪中线测设和断面测量方法。

重点：圆曲线、缓和曲线的要素计算和主点测设方法；切线支距法和偏角法的计算公式和测设方法；路线纵断面的基平、中平测量和横断面测量方法难点：缓和曲线的要素计算和主点测设方法；缓和曲线的切线支距法和偏角法的计算公式和测设方法。

§ 9.1 交点转点转角及里程桩的测设一、道路工程测量概述分为：路线勘测设计测量(route reconnaissance and design survey) 和道路施工测量(road construction survey) 。

（一）勘测设计测量(route reconnaissance and design survey)分为：初测(preliminary survey) 和定测(location survey)1、初测内容：控制测量(control survey) 、测带状地形图(topographical map of a zone) 和纵断面图(profile) 、收集沿线地质水文资料、作纸上定线或现场定线，编制比较方案，为初步设计提供依据。

2、定测内容：在选定设计方案的路线上进行路线中线测量(center line survey) 、测纵断面图(profile) 、横断面图(cross-section profile) 及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查，为施工图设计提供资料。

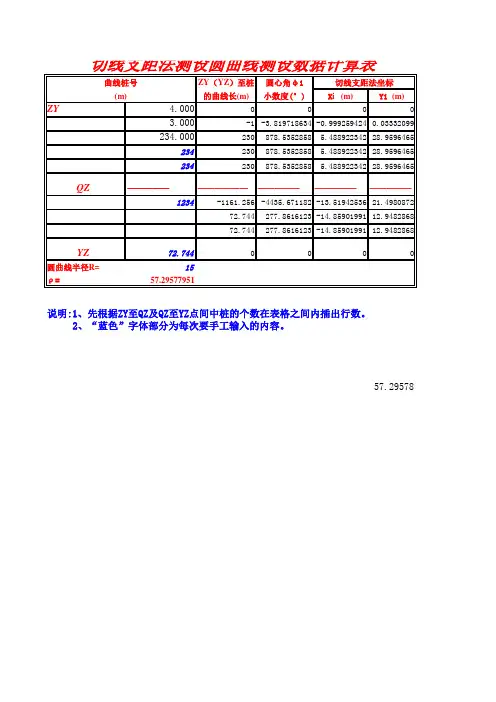
切线支距法
切线支距法是一种用于计算曲线弯曲半径的方法，它基于曲线上某一点的切线长度和曲率半径的关系。

在切线支距法中，首先要找到曲线上某一点的切线方向，这可以通过计算曲线在该点处的导数来实现。

一旦知道了切线方向，就可以将其延长，直到它与曲线相切。

此时，可以通过计算切线长度和曲线弯曲程度来确定曲线的弯曲半径。

具体来说，假设曲线上某一点处，切线向量为t，法向量为n，曲率半径为r。

则可以通过以下公式计算切线支距d：d=r*sin(θ)，其中，θ是切线向量和法向量之间的夹角。

切线支距法可以用于计算任意曲线的弯曲半径，包括圆弧、椭圆等。

在工程和科学领域中得到广泛应用，例如可以用于计算道路和铁路的弯曲半径，以确保车辆能够安全通过。

切线支距法
摘要：
1.切线支距法的定义
2.切线支距法的应用领域
3.切线支距法的计算方法
4.切线支距法的优缺点
5.切线支距法的实际应用案例
正文：
切线支距法是一种用于计算物体在斜面上的滑动距离和速度的方法，它主要应用于物理学、力学以及机械工程等领域。

切线支距法的定义是指，当物体在斜面上滑动时，其下滑的加速度与斜面切线间的距离。

具体来说，就是将物体在斜面上的滑动分解为沿斜面切线的滑动和垂直斜面切线的滑动，然后通过计算沿斜面切线的速度和时间，得出物体在斜面上的滑动距离。

切线支距法的计算方法主要包括以下步骤：首先，确定物体在斜面上的初始速度和加速度；其次，计算物体在斜面上的滑动时间；最后，根据滑动时间和初始速度，计算物体在斜面上的滑动距离。

切线支距法在实际应用中具有很多优点，比如计算简便、结果精确等。

它不仅可以用于计算物体在斜面上的滑动距离和速度，还可以用于分析物体在斜面上的滑动力学特性。

然而，切线支距法也存在一些缺点，比如在计算过程中需要假设物体在斜面上的滑动是均匀的，这可能会导致计算结果与实际情况存
在一定的偏差。

切线支距法的实际应用案例非常多，比如在机械工程中，它可以用于设计和分析各种斜面传动机构；在物理学和力学中，它可以用于研究物体在斜面上的滑动规律等。

切线支距法
（最新版）
目录
1.切线支距法的定义和原理
2.切线支距法的应用
3.切线支距法的优点和局限性
正文
切线支距法是一种用于测量物体长度的方法，主要通过测量物体切线与支点之间的距离来计算物体的长度。

这种方法的原理基于几何学中的切线定理，即在平面上，从一个点到一条直线的切线与该点到直线的垂线段之间的距离相等。

切线支距法在实际应用中具有广泛的应用。

例如，在工程测量中，常常需要测量建筑物或者道路的长度，这时候切线支距法就可以派上用场。

此外，切线支距法也可以用于测量物体的高度、宽度等尺寸。

切线支距法的优点在于操作简便，只需要测量切线与支点之间的距离，再根据切线定理计算出物体的长度即可。

而且，切线支距法的测量结果相对准确，只要操作得当，就能够获得较为精确的长度测量结果。

然而，切线支距法也存在一些局限性。

首先，切线支距法只适用于平面上的测量，对于立体物体的测量则无法使用。

其次，切线支距法的测量结果受到测量仪器精度的影响，如果仪器精度不高，那么测量结果也会存在偏差。

总的来说，切线支距法是一种简单而实用的测量方法，适用于各种平面测量场景。

第1页共1页。

切线支距法
（原创版）
目录
1.切线支距法的定义
2.切线支距法的应用
3.切线支距法的优缺点
4.切线支距法的发展前景
正文
切线支距法是一种在数学和物理学中经常使用的求解问题的方法。

切线支距法，顾名思义，是通过作图找到切线，然后通过切线的长度来求解问题的方法。

切线支距法最常见的应用是在力学中，特别是在静力学中。

例如，当一个物体放在一个斜面上时，我们可以通过作图找到斜面上物体所受到的支持力的切线，然后通过切线的长度来求解支持力的大小。

这种方法不仅可以求解支持力的大小，还可以求解支持力的方向，因此在实际问题中非常有用。

切线支距法的优点在于简单易懂，操作方便，而且结果准确。

只要作图准确，通过切线支距法求解出来的结果就可以直接应用到实际问题中。

但是，切线支距法也有其缺点，那就是它只适用于一些简单的问题，对于一些复杂的问题，切线支距法可能无法准确求解。

随着科学技术的发展，切线支距法的应用范围也在不断扩大。

现在，切线支距法不仅在数学和物理学中使用，还在工程学、地理学等学科中得到应用。

可以预见，随着科学技术的不断发展，切线支距法的应用前景将更加广阔。

总的来说，切线支距法是一种简单有效的求解问题的方法，它不仅可
以帮助我们解决实际问题，还可以帮助我们更好地理解科学原理。

程序计算在道路测量中的运用二、曲线坐标计算：传统计算坐标方法如下：.1 切线支距法：是以直缓点ZH或缓直点HZ为坐标原点，以过原点的切线为X 轴，过原点的曲率半径为Y轴，利用缓和曲线和圆曲线上各点的X、Y坐标测设曲线。

在缓和曲线上各点的坐标可按以下公式计算，即：X=L-L5/40R2Ls2Y=L3/6R Ls圆曲线上各点坐标的计算公式如下：X=Rsinφ+qY=R(1-cosφ)+p式中：φ=L180º/R*π+βo；L：该点到HY或YH的曲线长。

2.2偏角法用上述切线法算出缓和曲线和圆曲线上各点的坐标X、Y后，偏角法测设平曲线时，可将经纬仪置于ZH或HZ点进行测设。

设平曲线上任意一点P的支坐标为X、Y，则其偏角δ和弦长c的计算可由三角形得：δ=arcotY/Xc=√（X2+Y2）以上两种方法为传统计算法，图示及计算实例略。

此上方法计算过程繁琐,而且高速公路坐标为国家统一坐标系,要进行坐标转换容易产生错误,不利于施工过程的快速、准确开展,笔者在道路施工测量过程中,总结出了一套运用CASIO（fx-4800P）计算器程序计算缓和曲线上各点坐标,其特点是灵活、速度快、精度高。

.1 缓和曲线计中边桩推算思路：如上图：根据切线支距法公式先计算P点坐标，由P点坐标算出P-ZH距离，由起始方位角减P点的偏角δ得出ZH-P点方位角，后计算P点统一坐标；计算P点切线方位角计算左右边桩。

Xp=X0+Cos(F-δ)*√(X2+Y2); (δ=β0*L2*180/3Ls2π)Yp=Y0+Sin(F-δ)*√(X2+Y2)；（β0=Ls/2R*180/π）X边=Xp+Cos(90±F-β)*S; (β=L2/2RLs)Y边=Yp+Sin(90±F-β)*S。

式中X0、Y0，为ZH点线路统一坐标；X、Y为P点直角坐标；F为起始方位角；β为P点切线角；δ为P点偏角；L为P至ZH的缓和曲线长；S为P点左右边桩距离。