002 切线支距法专题(课堂PPT)
- 格式:ppt
- 大小:3.39 MB
- 文档页数:15

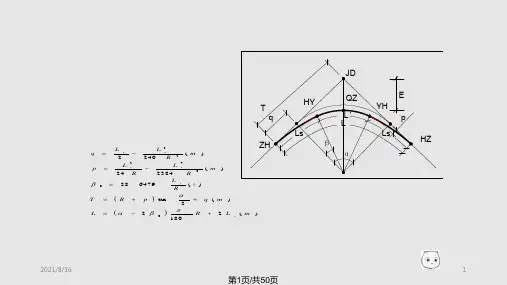
圆曲线计算-----切线⽀距法标志名称简称汉语拼⾳缩写交点JD转点ZD圆曲线起点直圆点ZY圆曲线中点曲中点QZ圆曲线终点圆直点YZ公切点GQ第⼀缓和曲线起点直缓点ZH第⼀缓和曲线终点缓圆点HY第⼆缓和曲线起点圆缓点YH第⼆缓和曲线终点缓直点HZ切线长转⾓(⾓度):α半径:R切线长:T=R*tan(α/2)曲线长:L=R*α *π/180外⽮距:E=R*(sec(α/2)-1)切曲差:D=2*T-L直圆点⾥程:ZY=JD-T圆直点⾥程:YZ=ZY+L曲中点⾥程:QZ=YZ-L/2交点⾥程(校核):JD=QZ+D/2切线⽀距法正算Pi点坐标Xi=R*SinφiYi=R*(1-Cosφi)(⾓度)φi=Li/R *180/π以曲线起点ZY或YZ为假定坐标原点,以切线为X轴,过假定坐标原点的半径为Y轴,设Pi点为曲线上待定点,该点⾄ZY点或YZ点弧长坐标为Xi,Yi 。
偏⾓法正算偏⾓(⾓度)Δi=Li/R/2 *180/π弦长Ci=2*R*Sin Δi弧弦差δi=L 3/R 2/24Ci=Li-δi δi=Li-Ci坐标系转换x=y=A=B=(y-y 0)cos α-(x-x 0)sin α偏⾓法是以曲线起点ZY 或终点YZ ⾄曲线上任⼀待定Pi 的弦线与切线T 之间的弦切⾓(这⾥称为偏⾓)Δi 和弦长Ci 或相邻邦点的⼩弦Ci'来确定Pi 点的位置。
x 0,y 0为建筑坐标系原点O'在国家或假定的勘测坐标系中坐标值;A ,B 为建筑坐标中的坐标;α为两坐标系的纵轴(X 轴与A 轴)的正向顺时针夹⾓x 0+Acos α-Bsin αy 0+Bcos α+Asin α(x-x 0)cos α+(y-y 0)sin α倒算Pi 点坐标Xi=R*Sin φiYi=R*(Cos φi-1)(⾓度)φi=Li/R *180/πLi为正倒算原点,以切线为X轴,设Pi 点为曲线上长坐标为Xi ,Yi 。

切线支距法
(最新版)
目录
1.切线支距法的定义和原理
2.切线支距法的应用
3.切线支距法的优点和局限性
正文
切线支距法是一种用于测量物体长度的方法,主要通过测量物体切线与支点之间的距离来计算物体的长度。
这种方法的原理基于几何学中的切线定理,即在平面上,从一个点到一条直线的切线与该点到直线的垂线段之间的距离相等。
切线支距法在实际应用中具有广泛的应用。
例如,在工程测量中,常常需要测量建筑物或者道路的长度,这时候切线支距法就可以派上用场。
此外,切线支距法也可以用于测量物体的高度、宽度等尺寸。
切线支距法的优点在于操作简便,只需要测量切线与支点之间的距离,再根据切线定理计算出物体的长度即可。
而且,切线支距法的测量结果相对准确,只要操作得当,就能够获得较为精确的长度测量结果。
然而,切线支距法也存在一些局限性。
首先,切线支距法只适用于平面上的测量,对于立体物体的测量则无法使用。
其次,切线支距法的测量结果受到测量仪器精度的影响,如果仪器精度不高,那么测量结果也会存在偏差。
总的来说,切线支距法是一种简单而实用的测量方法,适用于各种平面测量场景。
第1页共1页。

切线支距法
切线支距法是一种用于计算曲线弯曲半径的方法,它基于曲线上某一点的切线长度和曲率半径的关系。
在切线支距法中,首先要找到曲线上某一点的切线方向,这可以通过计算曲线在该点处的导数来实现。
一旦知道了切线方向,就可以将其延长,直到它与曲线相切。
此时,可以通过计算切线长度和曲线弯曲程度来确定曲线的弯曲半径。
具体来说,假设曲线上某一点处,切线向量为t,法向量为n,曲率半径为r。
则可以通过以下公式计算切线支距d:d=r*sin(θ),其中,θ是切线向量和法向量之间的夹角。
切线支距法可以用于计算任意曲线的弯曲半径,包括圆弧、椭圆等。
在工程和科学领域中得到广泛应用,例如可以用于计算道路和铁路的弯曲半径,以确保车辆能够安全通过。

切线支距法
(原创版)
目录
1.切线支距法的定义
2.切线支距法的应用
3.切线支距法的优缺点
4.切线支距法的发展前景
正文
切线支距法是一种在数学和物理学中经常使用的求解问题的方法。
切线支距法,顾名思义,是通过作图找到切线,然后通过切线的长度来求解问题的方法。
切线支距法最常见的应用是在力学中,特别是在静力学中。
例如,当一个物体放在一个斜面上时,我们可以通过作图找到斜面上物体所受到的支持力的切线,然后通过切线的长度来求解支持力的大小。
这种方法不仅可以求解支持力的大小,还可以求解支持力的方向,因此在实际问题中非常有用。
切线支距法的优点在于简单易懂,操作方便,而且结果准确。
只要作图准确,通过切线支距法求解出来的结果就可以直接应用到实际问题中。
但是,切线支距法也有其缺点,那就是它只适用于一些简单的问题,对于一些复杂的问题,切线支距法可能无法准确求解。
随着科学技术的发展,切线支距法的应用范围也在不断扩大。
现在,切线支距法不仅在数学和物理学中使用,还在工程学、地理学等学科中得到应用。
可以预见,随着科学技术的不断发展,切线支距法的应用前景将更加广阔。
总的来说,切线支距法是一种简单有效的求解问题的方法,它不仅可
以帮助我们解决实际问题,还可以帮助我们更好地理解科学原理。


切线支距法
摘要:
1.切线支距法简介
2.切线支距法的应用
3.切线支距法在实际问题中的应用案例
4.总结
正文:
切线支距法是一种在数学和物理学中常用的方法,它可以用来解决曲线运动、力学和电磁学等领域的问题。
这种方法利用切线的概念,通过计算切线与坐标轴的交点,可以确定曲线运动物体的位置和速度。
切线支距法的应用十分广泛。
在物理学中,它可以用来解决平抛运动、圆周运动等问题。
在数学中,它可以用来解决微积分、线性代数等问题。
此外,在计算机图形学、工程学和天文学等领域,切线支距法也发挥着重要作用。
以平抛运动为例,假设一个物体在水平方向上以初速度v0投掷,竖直方向上受到重力加速度g的作用。
我们可以通过切线支距法来计算物体在空中的运动轨迹。
首先,我们需要计算物体在水平方向和竖直方向上的速度。
水平方向上的速度始终保持不变,即v0。
竖直方向上的速度可以通过公式vy = gt来计算,其中t为时间。
接下来,我们需要计算物体在各个时刻的切线方程。
根据初速度和加速度,我们可以得到物体在时刻t的切线方程为:y - y0 = v0t - 0.5gt^2。
与x 轴相交的点即为物体在时刻t的水平位置。
通过计算这个交点,我们可以得到
物体在空中的运动轨迹。
在实际问题中,切线支距法的应用可以帮助我们更好地理解物体的运动规律,从而为实际问题提供解决方案。
例如,在导弹轨迹规划中,通过使用切线支距法,可以预测导弹的飞行轨迹,从而提高导弹的命中精度。
总之,切线支距法是一种在多个领域具有重要应用价值的数学方法。

切线支距法
摘要:
1.切线支距法的定义
2.切线支距法的应用领域
3.切线支距法的计算方法
4.切线支距法的优缺点
5.切线支距法的实际应用案例
正文:
切线支距法是一种用于计算物体在斜面上的滑动距离和速度的方法,它主要应用于物理学、力学以及机械工程等领域。
切线支距法的定义是指,当物体在斜面上滑动时,其下滑的加速度与斜面切线间的距离。
具体来说,就是将物体在斜面上的滑动分解为沿斜面切线的滑动和垂直斜面切线的滑动,然后通过计算沿斜面切线的速度和时间,得出物体在斜面上的滑动距离。
切线支距法的计算方法主要包括以下步骤:首先,确定物体在斜面上的初始速度和加速度;其次,计算物体在斜面上的滑动时间;最后,根据滑动时间和初始速度,计算物体在斜面上的滑动距离。
切线支距法在实际应用中具有很多优点,比如计算简便、结果精确等。
它不仅可以用于计算物体在斜面上的滑动距离和速度,还可以用于分析物体在斜面上的滑动力学特性。
然而,切线支距法也存在一些缺点,比如在计算过程中需要假设物体在斜面上的滑动是均匀的,这可能会导致计算结果与实际情况存
在一定的偏差。
切线支距法的实际应用案例非常多,比如在机械工程中,它可以用于设计和分析各种斜面传动机构;在物理学和力学中,它可以用于研究物体在斜面上的滑动规律等。