计算传热学 第3讲 数学模型与求解区域的离散化 习题课 Patanker 3.1

传热学--第三章第三节一维非稳态导热问题§3 — 3 一维非稳态导热的分析解本节介绍第三类边界条件下：无限大平板、无限长圆柱、球的分析解及应用。

如何理解无限大物体，如：当一块平板的长度、宽度>> 厚度时，平板的长度和宽度的边缘向四周的散热对平板内的温度分布影响很少，以至于可以把平板内各点的温度看作仅是厚度的函数时，该平板就是一块“无限大”平板。

若平板的长度、宽度、厚度相差较小，但平板四周绝热良好，则热量交换仅发生在平板两侧面，从传热的角度分析，可简化成一维导热问题。

一、无限大平板的分析解已知：厚度的无限大平板，初温t0，初始瞬间将其放于温度为的流体中，而且>t0，流体与板面间的表面传热系数为一常数。

试确定在非稳态过程中板内的温度分布。

解：如图3-5 所示，平板两面对称受热，所以其内温度分布以其中心截面为对称面。

对于x 0 的半块平板，其导热微分方程：(0<x< , )定解条件：t(x,0)= t0(0 x )（边界条件）（边界条件）引入过余温度：则（0<x< , ）(3-9)(x,0)= (0 x ) （初始条件）（边界条件）（边界条件）对偏微分方程分离变量求解得：（3-10 ）其中离散值是下列超越方程的根，称为特征值。

其中Bi 是以特征长度为的毕渥数。

由此可见：平板中的无量纲过余温度与三个无量纲数有关：以平板厚度一半为特征长度的傅立叶数、毕渥数及即：（3-12)二、非稳态导热的正规状况阶段1 、平板中任一点的过余温度与平板中心的过余温度的关系前述得到的分析解是一个无穷级数，计算工作量大，但对比计算表明，当Fo>0.2 时，采用该级数的第一项与采用完整的级数计算平板中心温度的误差小于1% ，因此，当Fo>0.2时，采用以下简化结果：（3-13 ）其中特征值之值与Bi 有关。

由上式（3-13 ）可知：Fo>0.2 以后平板中任一点的过余温度(x ，τ) 与平板中心的过余温度(0 ，τ)=（τ ）之比为：（3-14 ）此式反映了非稳态导热过程中一种很重要的物理现象：即当Fo>0.2 以后，虽然(x ，τ) 与（τ ）各自均与τ 有关，但其比值则与τ 无关，而仅取决于几何位置（x/ ）及边界条件（Bi ）。

【最新整理，下载后即可编辑】第三章思考题1. 试说明集中参数法的物理概念及数学处理的特点答：当内外热阻之比趋于零时，影响换热的主要环节是在边界上的换热能力。

而内部由于热阻很小而温度趋于均匀，以至于不需要关心温度在空间的分布，温度只是时间的函数，数学描述上由偏微分方程转化为常微分方程、大大降低了求解难度。

2. 在用热电偶测定气流的非稳态温度场时,怎么才能改善热电偶的温度响应特性?答：要改善热电偶的温度响应特性，即最大限度降低热电偶的时间常数hA cvc ρτ=,形状上要降低体面比，要选择热容小的材料，要强化热电偶表面的对流换热。

3. 试说明”无限大平板”物理概念,并举出一二个可以按无限大平板处理的非稳态导热问题答；所谓“无限大”平板，是指其长宽尺度远大于其厚度，从边缘交换的热量可以忽略不计，当平板两侧换热均匀时，热量只垂直于板面方向流动。

如薄板两侧均匀加热或冷却、炉墙或冷库的保温层导热等情况可以按无限大平板处理。

4.什么叫非稳态导热的正规状态或充分发展阶段?这一阶段在物理过程及数学处理上都有些什么特点?答：非稳态导热过程进行到一定程度,初始温度分布的影响就会消失，虽然各点温度仍随时间变化,但过余温度的比值已与时间无关，只是几何位置(δ/x)和边界条件(Bi数)的函数，亦即无量纲温度分布不变，这一阶段称为正规状况阶段或充分发展阶段。

这一阶段的数学处理十分便利，温度分布计算只需取无穷级数的首项进行计算。

5.有人认为,当非稳态导热过程经历时间很长时,采用图3-7记算所得的结果是错误的.理由是：这个图表明,物体中各点的过余温度的比值与几何位置及Bi有关,而与时间无关.但当时间趋于无限大时,物体中各点的温度应趋近流体温度,所以两者是有矛盾的。

你是否同意这种看法,说明你的理由。

答：我不同意这种看法，因为随着时间的推移，虽然物体中各点过余温度的比值不变但各点温度的绝对值在无限接近。

这与物体中各点温度趋近流体温度的事实并不矛盾。

第三章 非稳态导热(unsteady state conduction)物体的温度随时间而变化的导热过程称非稳态导热。

0≠τ∂∂t，任何非稳态导热过程必然伴随着加热或冷却过程。

根据物体内温度随时间而变化的特征不同，非稳态导热过程可分为两类：（1）周期性导热（periodic unsteady conduction ）：物体的温度按照一定的周期发生变化； 如建筑物的外墙和屋顶温度的变化。

（2）瞬态导热(transient conduction)：物体的温度随时间不断升高或降低，在经历相当长时间后，物体的温度逐渐趋于周围介质的温度，最终达到热平衡。

分析非稳态导热的任务：找出温度分布和热流密度随时间和空间的变化规律。

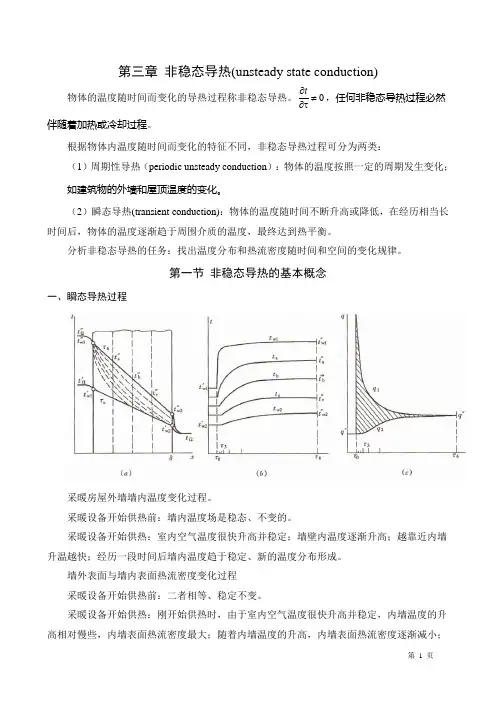
第一节 非稳态导热的基本概念一、瞬态导热过程采暖房屋外墙墙内温度变化过程。

采暖设备开始供热前：墙内温度场是稳态、不变的。

采暖设备开始供热：室内空气温度很快升高并稳定；墙壁内温度逐渐升高；越靠近内墙升温越快；经历一段时间后墙内温度趋于稳定、新的温度分布形成。

墙外表面与墙内表面热流密度变化过程 采暖设备开始供热前：二者相等、稳定不变。

采暖设备开始供热：刚开始供热时，由于室内空气温度很快升高并稳定，内墙温度的升高相对慢些，内墙表面热流密度最大；随着内墙温度的升高，内墙表面热流密度逐渐减小；随着外墙表面的缓慢升高，外墙表面热流密度逐渐增大；最终二者相等。

上述非稳态导热过程，存在着右侧面参与换热与不参与换热的两个不同阶段。

（1）第一阶段（右侧面不参与换热）是过程开始的一段时间，特点是：物体中的一部分温度已经发生变化，而另一部分仍维持初始状态时的温度分布（未受到界面温度变化的影响），温度分布显现出部分为非稳态导热规律控制区和部分为初始温度区的混合分布，物体内各处温度随时间的变化率是不一样的，即：在此阶段物体温度分布受t分布的影响较大，此阶段称非正规状况阶段或初始阶段（initialregime）。

（2）第二阶段（右侧面参与换热）当右侧面参与换热以后，物体中的温度分布不受t影响，主要取决于边界条件及物性。

第四版传热学第三章习题解答第三章思考题1. 试说明集总参数法的物理概念及数学处理的特点答：当内外热阻之比趋于零时，影响换热的主要环节是在边界上的换热能力。

而内部由于热阻很小而温度趋于均匀，以至于不需要关心温度在空间的分布，温度只是时间的函数，数学描述上由偏微分方程转化为常微分方程、大大降低了求解难度。

2. 在用热电偶测定气流的非稳态温度场时,怎么才能改善热电偶的温度响应特性?答：要改善热电偶的温度响应特性，即最大限度降低热电偶的时间常数hA cvc ρτ=,形状上要降低体面比，要选择热容小的材料，要强化热电偶表面的对流换热。

3. 试说明”无限大平板”物理概念,并举出一二个可以按无限大平板处理的非稳态导热问题答；所谓“无限大”平板，是指其长宽尺度远大于其厚度，从边缘交换的热量可以忽略不计，当平板两侧换热均匀时，热量只垂直于板面方向流动。

如薄板两侧均匀加热或冷却、炉墙或冷库的保温层导热等情况可以按无限大平板处理。

4. 什么叫非稳态导热的正规状态或充分发展阶段?这一阶段在物理过程及数学处理上都有些什么特点?答：非稳态导热过程进行到一定程度,初始温度分布的影响就会消失，虽然各点温度仍随时间变化,但过余温度的比值已与时间无关，只是几何位置(δ/x )和边界条件(Bi 数) 的函数，亦即无量纲温度分布不变，这一阶段称为正规状况阶段或充分发展阶段。

这一阶段的数学处理十分便利，温度分布计算只需取无穷级数的首项进行计算。

5. 有人认为,当非稳态导热过程经历时间很长时,采用图3-7记算所得的结果是错误的.理由是：这个图表明,物体中各点的过余温度的比值与几何位置及Bi 有关,而与时间无关.但当时间趋于无限大时,物体中各点的温度应趋近流体温度,所以两者是有矛盾的。

你是否同意这种看法,说明你的理由。

答：我不同意这种看法，因为随着时间的推移，虽然物体中各点过余温度的比值不变但各点温度的绝对值在无限接近。

这与物体中各点温度趋近流体温度的事实并不矛盾。