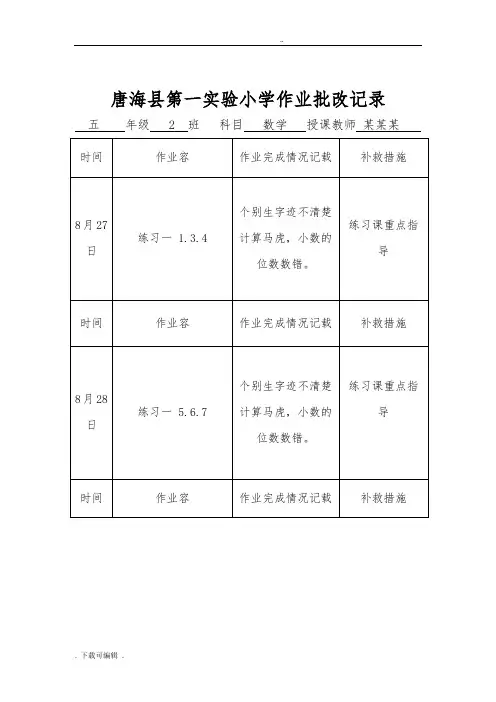
数学实验8月13日作业

2024届高三年级第一学期周考（实验班）数学试卷油印： 日期： 2023.8.6一、单项选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中， 只有一项是符合题目要求的。

A ．(],2−∞B ．[)2,+∞C ．[]2,4D ．(]0,22．已知a b <，则（ ）3．已知函数()22,1,x x x af x x x a +≤= −>，则01a <<是()f x 有3个零点的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．若命题：“存在整数x 使不等式()()2440kx k x <−−−成立”是假命题，则实数k 的取值范围是（ ）A ．-2B ．-1C ．1D ．26．已知函数3ln(1),0()31,0x x f x x x x +> = −+≤ ，关于x 的方程()()22210f x mf x m −+ − = 恰有4个零点，则m 的取值范围是（ ）二、多项选择题：本题共4小题，每小题5分，共20分。

在每小题给出的选项中，有多项符合题目要求。

全部选对的得5分，有选错的得0分，部分选对的得2分。

9．下列说法正确的是（）10．函数()21e xy kx=+的图像可能是（）A．B．C．D．11．已知函数()22lnf x a x x=+，则下列说法正确的是（）A．()()=f x f x−B．()f x的最小值为2eC．()()f x f x−的最小值为4D．()f x在区间()1,0−上单调递增三、填空题：本题共4小题，每小题5分，共20分。

(1)给出以下四个函数模型：参考答案：x（天) 1 14 18 22 26 30 Q x122 135 139 143 139 135 ()。

五年级数学日记(通用15篇)8月17日星期天我家的电费很多，你想知道原因吗?就让我来告诉你吧。

因为我晚上睡觉的时候从来不会关灯的，你相信吗?对了，我从来都不会关灯的，有时候我爸爸帮我关掉，我也会偷偷地把灯打开，我只要听到一点点声音或者发现灯关着，我都会感到很害怕。

其他同学都说开着灯睡不着的，但是我也不知道为什么我正好跟他们相反。

我的爸爸妈妈也为此觉得很困扰，他们已经为我讲了许许多多的道理了，听得我耳朵都快出茧了，但是我还是改不掉这个坏习惯，呜呜。

就这样，爸爸教会了我怎么看电表，电表是这样看的：各种电能表，所显示的数字都是到目前为止用去的电能。

为了计量一段时间消耗的电能，必须记录这段时间起始和结束时电能表上的示数。

电能表的计数器上前后两次读数之差，就是这段时间内用电的度数。

电能表是有一排数字吗，最后一个，就是和前面颜色不一样的，是小数。

比如电能表上的那些数是00023，就是用了2.3度电。

不过为了计算电费方便，读数时常常只读整数，小数略去不计。

从此我晚上睡觉就不开灯了，知道为爸爸妈妈省钱了。

8月23日星期六我喜欢做一些数学题目，因为我觉得数学有趣又实用，并且和我们的生活息息相关。

今天我在一本课外数学书上看到这样一道题，来和大家分享一下。

题目是这样的：“我们国家大约有13亿的人口，如果我们每人每天节约1角钱，这样全国每天就可以节约1300万元，如果把这笔钱用在失学儿童身上，就可以让1800位小朋友去上学。

”看了上面的信息，我想，真是人多力量大啊。

但我又想了想：如果我们国家的13亿人口，每人每天浪费一滴水，那么一共约浪费了13亿滴水，大家想一想13亿滴水大约有多重呢?我做了一个小实验：用一个杯子在水龙头下面积了100滴水，再用天平秤秤了一下，100滴水重20克，我动笔算了一下：1300000000÷100×20=260000000克260000000克=260吨真是不算不知道，一算吓一跳呀。

郑州市宇华实验学校2024—2025学年高三上学期第一次月考数学注意事项：1．答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚．2．每道选择题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号．在试题卷上作答无效．3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．4．考试结束后，请将本试卷和答题卡一并交回．一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知,0,2παβ⎛⎫∈ ⎪⎝⎭，则“1cos()4αβ-<”是“1cos sin 4αβ+<”的（ ）A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2．已知实数x ,y ,z 满足e ln e y x x y =且1e lne z x z x =,若01y <<,则（ ）A ．x y z >> B ．x z y >> C ．y z x >>D ．y x z >>3．已知函数2||,(),x m x m f x x x m +≤⎧=⎨>⎩，若存在实数b ,使得关于x 的方程()f x b =有三个不同的根，则实数m 的取值范围是（）A ．(0,2) B ．(,2)(0,2)-∞-C ．(2,0)-D ．(2,0)(2,)-+∞ 4．定义：两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值．在棱长为1的正方体1111ABCD A B C D -中，直线BD 与1CB 的距离为（ ）A ．1BC ．12D5．在ABC △中，内角A ,B ,C 所对的边分别为a ,b ,c ,ABC △的面积为S ,若22cos bc A b c +=+,则sin cos cos A B C=+（ ）A B ．12C D6．已知z 为复数，且||1z =,则|3i |z -的取值范围是（）A ．[]2,3B ．[]3,4C ．[]2,4D ．4⎡⎤⎣⎦7．若样本空间Ω中的事件123,,A A A 满足()()()()()223113231221,,,4356P A P A A P A P A A P A A =====∣∣∣，则()13P A A =（ ）A ．114 B ．17 C ．27 D ．5288．已知a ,b 均为正实数，若直线y x a =-与曲线ln(2)y x b =+相切，则2a b ab ab ++的最小值是（ ）A ．8 B ．9 C ．10 D ．11二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，有选错的得0分，若只有2个正确选项，每选对1个得3分；若只有3个正确选项，每选对1个得2分．9．下列函数()f x 的最小值为2的是（）A ．2()21f x x x =--+B ．()23()log 210f x x x =++C ．()22x x f x -=+D ．1()32x f x -=+10．如图，在棱长为的正方体1111ABCD A B C D -中，点P 是平面11A BC 内一个动点，且满足13PD PB +=+,则下列结论正确的是（ ）A ．1B D PB ⊥B ．直线1B P 与平面11A BC 所成角为定值C ．点P 的轨迹的周长为D ．三棱锥11P BB C -体积的最大值为11．对于函数3()()ln ,()f x f x x x g x x ==，则下列说法正确的是（ ）A ．()g x 在x =12eB ．(2)g g >C ．()g x 只有一个零点D ．若方程2()kf x x =恰好只有一个实数根，则0k <三、填空题：本大题共3个小题，每小题5分，共15分．12．一批小麦种子的发芽率是0.7，每穴只要有一粒发芽，就不需补种，否则需要补种．则每穴至少种_________粒，才能保证每穴不需补种的概率大于97%．()lg 30.48≈13．已知函数2()2sin cos 0)222xxxf x ωωωω=-+>的最小正周期为T ,若223T ππ<<，且3π是()f x 的一个极值点，则ω=_________．14．过点P 作斜率为k 的直线l 交圆22:8E x y +=于,A B 两点，动点Q 满足||||||||PA QA PB QB =，若对每一个确定的实数k ,记||PQ 的最大值为max d ,则当k 变化时，max d 的最小值为_________．四、解答题：本大题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15．（13分）各项都为整数的数列{}n a 满足272,4a a =-=,前6项依次成等差数列，从第5项起依次成等比数列．（1）求数列{}n a 的通项公式；（2）求出所有的正整数m ,使得1212m m m m m m a a a a a a ++++++=．16．（15分）如图，正方体111ABCD A B C D -．（1）求证：1A B ⊥面1A BC ;（2）若E 为线段1AC 的中点，求平面ABE 与平面BCE 所成锐二面角的大小．17．（15分）书籍是精神世界的入口，阅读让精神世界闪光，阅读逐渐成为许多人的一种生活习惯，每年4月23日为世界读书日．某研究机构为了解某地年轻人的阅读情况，通过随机抽样调查了100位年轻人，对这些人每天的阅读时间（单位：分钟）进行统计，得到样本的频率分布直方图，如图所示．（1）根据频率分布直方图，估计这100位年轻人每天阅读时间的平均数x （单位：分钟）；（同一组数据用该组数据区间的中点值表示）（2）若年轻人每天阅读时间X 近似地服从正态分布(,100)N μ,其中μ近似为样本平均数x ,求(6494)P X <≤；（3）为了进一步了解年轻人的阅读方式，研究机构采用分层抽样的方法从每天阅读时间位于分组[50,60),[60,70),[80,90)的年轻人中抽取10人，再从中任选3人进行调查，求抽到每天阅读时间位于[80,90)的人数ξ的分布列和数学期望．附参考数据：若，则①()0.6827P X μδμδ-<≤+=；②(22)0.9545P X μδμδ-<≤+=；③(33)0.9973P X μδμδ-<≤+=．18．（17分）已知圆22:(1)1M x y ++=,圆22:(1)9N x y -+=动圆P 与圆M 外切并且与圆N 内切，圆心P 的轨迹为曲线C ．（1）求曲线C 的方程；（2）设不经过点Q 的直线l 与曲线C 相交于A ,B 两点，直线QA 与直线QB 的斜率均存在且斜率之和为2-，直线AB 是否过定点，若过定点，写出定点坐标．19．（17分）已知函数()ln f x x x =．（1）求曲线()y f x =在点(1,(1))f 处的切线方程；（2）求()f x 的单调区间；（3）若对于任意1,x e e ⎡⎤∈⎢⎥⎣⎦，都有()1f x ax ≤-,求实数a 的取值范围．数学参考答案一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．【答案】B 【解析】,0,2παβ⎛⎫∈ ⎪⎝⎭，则0cos 1,0sin 1βα<<<<,所以cos()cos cos sin sin cos sin αβαβαβαβ-=+<+,所以由1cos()4αβ-<不能推出1cos sin 4αβ+<，充分性不成立；反之，11cos sin cos()44αβαβ+<⇒-<成立，即必要性成立；,0,2παβ⎛⎫∴∈ ⎪⎝⎭,则“1cos()4αβ-<”是“1cos sin 4αβ+<”的必要不充分条件．故选：B ．2．【答案】A【解析】由e ln e y xx y =得ln e ex y x y =，由1e ln e z x z x =得ln e e x z x z -=，因此e ey z y z -=，又01y <<,所以0e e z y z y =-<，又e 0z >,所以0z <,利用01y <<得ln 0e ex y x y =>，又e 0x >,所以ln 0x >,即1x >,所以10x y z >>>>,即x y z >>．故选A ．3．【答案】B【解析】分情况讨论，当0m >时，要使()f x b =有三个不同的根，则2|2|020m m m m ⎧>⇒<<⎨>⎩;当0m <时，要使()f x b =有三个不同的根，同理可知，需要2|2|20m m m m ⎧>⇒<-⎨<⎩．当0m =时，两个分段点重合，不可能有三个不同的根，故舍去．所以m 的取值范围是(,2)(0,2)-∞- ．故选B ．4．【答案】D【解析】设M 为直线BD 上任意一点，过M 作1MN CB ⊥,垂足为N ,可知此时M 到直线1CB 距离最短，设111,DM DB DA DC CN CB DA DA DD λλλμμμμ==+===+ ，1(1)()MN DN DM DC CN DM DC DA DD λμλμ=-=+-=-+-+ ，11CB DA DD =+ ,因为1MN CB ⊥,所以10MN CB ⋅= ,即()11(1)()0DC DA DD DA DD λμλμ⎡⎤-+-+⋅+=⎣⎦ ，所以0μλμ-+=，即=2λμ=，所以1(12)MN DC DA DD μμμ=--+ ,所以||MN === ，所以当13μ=时，||MN，所以直线BD 与1CB．故选：D ．5．【答案】D【解析】由22cos bc A b c +=+22sin cos A bc A b c +=+,22cos 2sin 6b c b c A A A bc c b π+⎛⎫+=⇒+=+ ⎪⎝⎭，由于2,2sin 26b c A c b π⎛⎫+≥+≤ ⎪⎝⎭，当且仅当b c c b =，以及62A ππ+=时，等号成立，结合2sin 6b c A c b π⎛⎫+=+ ⎪⎝⎭，因此2sin 26b c A c b π⎛⎫+=+= ⎪⎝⎭，且b c c b =，以及3A π=，故3B C π==，因此sin cos cos A B C ==+故选D ．6．【答案】C【解析】因为复数z 满足||1z =,不妨设cos isin ,R z θθθ=+∈,则|3i ||cos i(sin 3)|z θθ-=+-==．因为sin [1,1]θ∈-，所以[2,4]，所以|3i |z -的取值范围是[2,4]．故选：C ．7．【答案】A【解折】因为()()()()()113223231221,,,4356P A P A A P A P A A P A A =====∣∣∣，所以()()()()()2323323P A P A P A A P A P A A =+∣∣()()()()()3233231P A P A A P A PA A =+-∣∣,解得()357P A =，()()31311P A A P A A =-∣∣()()()()()133131111P A A P A P A A P A P A =-=-∣()()()13311P A A P A A P A =∣()()()1133115144714P A P A A P A =-=-⨯=∣．故选：A ．8．【答案】C 【解析】由于直线y x a =-与曲线ln(2)y x b =+相切，设切点为(,)m n ,而12y x b '=+，故112ln(2)m b m b m a⎧=⎪+⎨⎪+=-⎩,解得m a =,故21,,a b a b +=均为正实数，故22122(2)16610a b ab a b a b ab b a ba ++⎛⎫=+++=++≥+= ⎪⎝⎭，当且仅当22a b b a =，结合21a b +=,即得13a b ==时等号成立，故2a b ab ab ++的最小值是10，故选：C ．二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，有选错的得0分，若只有2个正确选项，每选对1个得3分；若只有3个正确选项，每选对1个得2分．9．【答案】BC【解析】对于A,由二次函数性质可知，()f x 无最小值，A 错误；对于B,令22210(1)99t x x x =++=++≥，因为3log y t =单调递增，所以3()log 92f x ≥=,当1x =-时等号成立，所以min ()2f x =，B 正确；对于C,因为20x >，所以1()222x x f x =+≥，当且仅当122x x =，即0x =时，等号成立，所以min ()2f x =，C 正确；对于D,由指数函数性质可知，130x ->,所以1()322x f x -=+>,D 错误．故选：BC ．10．【答案】ABD【解析】对于A,连接11B D ,因为四边形1111A B C D 为正方形，则1111A C B D ⊥,因为1DD ⊥平面111111,A B C D A C ⊂平面1111A B C D ,则111A C DD ⊥,因为111111,B D DD D B D = 、1DD ⊂平面11B DD ,所以11A C ⊥平面11B DD ,1B D ⊂平面11B DD ,所以111B D A C ⊥,同理可得11B D A B ⊥,因为1111111,A C A B A A C A B =⊂ 、平面11A BC ,所以1B D ⊥平面11A BC ,因为PB ⊂平面11A BC ,所以1B D PB ⊥,故A 正确；对于C,由A 选项知1B D ⊥平面11A BC ,设1B D 平面11A BC E =,即1B E ⊥平面11,A BC DE ⊥平面11A BC ,因为1111111116,A B BC AC A B BB B C ======,所以三棱锥111B A BC -为正三棱锥，因为1B E ⊥平面11A BC ,则E 与正11A BC △的中心，则12sin 3A BBE π==，所以1B E ==,因为1B D ==所以DE =,因为13PD PB +=+,3=+,3+=+(3=+-,两边平方化简可得0)PE PE =>,因为E 点到等边三角形11A BC 的边的距离为163PE ==,所以点P 的轨迹是在11A BC △内，且以E所以点P 的轨迹的周长为，故C 错误；对于B,由选项C 可知，点P 的轨迹是在11A BC △内，且以E 的圆，EP =1B E =1B E ⊥平面11A BC ,所以1B PE ∠就是直线1B P 与平面11A BC 所成角，所以11tan B E B PE PE ∠===102B PE π<∠<，所以直线1B P 与平面11A BC 所成角为定值，故B 正确；对于D,因为点E 到直线1BC点P 到直线1BC =，故1BPC △的面积的最大值为162⨯=,因为1B E ⊥平面11A BC ,则三棱锥11B BPC -体积的最大值为13⨯=，故D 正确．故选：ABD ．11．【答案】AC【解新】对于A ，函数32()ln ()ln ,()f x xf x x xg x x x===，则24312ln 12ln (),0x x xxx g x x x x⨯--'==>,令()0g x '=，即12ln 0x -=,解得x =当0x <<时，()0g x '>,故函数()g x在上为单调递增函数，当x >时，()0g x '<，故函数()g x在)+∞上为单调递减函数，故()g x在x =处取得极大值12eg =,故选项A 正确；对于B,当x >()0g x '<,故函数()g x在)+∞上为单调递减函数，所以(2)g g <，故选项B 错误；对于C,令函数()0g x =,则ln 0x =,解得1x =,所以函数()g x 只有一个零点，故选项C 正确；对于D,易知1x =不是方程的解；当1x ≠时，()0f x ≠，方程2()kf x x =恰好只有一个实数根，等价于y k =和()ln xh x x=只有一个交点，则2ln 1(),0(ln )x h x x x -'=>且1x ≠，令()0h x '=,即ln 10x -=,解得e x =,当e x >时，()0h x '>,故函数()h x 在(e,)+∞上为单调递增函数，当01,1e x x <<<<时，()0h x '<,故函数()h x 在(0,1)，(1,e)上均单调递减，1x =是一条渐近线，当01x <<时，()0h x <,当1e x <<时，()0h x >,故()h x 在e x =处取得极小值(e)e h =,结合条件可知k e =或0k <,故选项D 错误；故选：AC．三、填空题：本大题共3个小题，每小题5分，共15分．12．【答案】3【解析】记事件A 为“种一粒种子，发芽”，则()0.7,(0.3P A P A ==设每穴种n 粒，则相当于做了n 次独立重复实验，记事件B 为“每穴至少有一粒发芽”，则00()C 0.7(10.7)0.3,()1()10.3n n n n P B P B P B =-==-=-若保证每穴不需补种的概率大于97%，则10.30.97n ->即0.30.03n <，两边取对数得，lg 0.3lg 0.03n <,即(lg 31)lg 32n -<-又lg 30.48≈，则lg 322.92lg 31n ->≈-，又n 为整数，则每穴至少种3粒，才能保证每穴不需补种的概率大于97%．故答案为：3．13．【答案】72【解析】2()2sincossin 2sin 2223xxxf x x x x ωωωπωωω⎛⎫=-+==+ ⎪⎝⎭所以()2sin 3f x x πω⎛⎫=+ ⎪⎝⎭的最小正周期为2T πω=，于是2223πππω<<，解得34ω<<，因为3π是()f x 的一个极值点，则,Z 332k k πππωπ+=+∈，解得13,2k k Z ω=+∈,所以1k =时，7(3,4)2ω=∈．故答案为：72．14．【答案】2【解析】由题设1348+=<，即P 在圆22:8E x y +=内，令||||P APA PB P Bλ'=='且1λ≠，显然P 是A ,B 内分比点，若P '为外分比点，则||||P APA PB P Bλ'==',此时PP '的中点C 为P ,Q 所在阿氏圆的圆心，对于每一个确定的实数,||k PQ 最大值为max d PP '=,即,Q P '重合时max d 为对应圆直径，根据圆的对称性，如上图，讨论1λ>的情况，而||2OP =,当AB为直径时，max ||3||PA PB λ===+,3=+可得4P B '=-故||PQ 的最大值为max ||2d PP P B PB ''==+=；当AB不为直径时134||AB λ<<+<<,且,||AB λ增减趋势相同，由||P A P B AB P B P Bλ''+==''，得||1AB P B λ'=-，显然||1AB P B λ'=-接近于1时P B '趋向无穷大，此时||PQ 的最大值为max d 趋向无穷大．综上，max d 的最小值是2．故答案为：2．四、解答题：本大题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15．（13分）【答案】（1）()*54,14N 2,5n n n n a n n --≤≤⎧=∈⎨≥⎩；（2）{1,3}【解析】（1）设前6项的公差为d ,所以2151612,4,5a a d a a d a a d =+=-=+=+，所以()()12112445a d a d a d +=-⎧⎪⎨+⨯=+⎪⎩，化简可得(43)(1)0d d --=,所以1d =或34，又因为{}n a 各项均为整数，所以d 为整数，所以1d =,当*14,n n ≤≤∈N 时，2(2)4n a a n d n =+-=-,当*5,N n n ≥∈时，555621,2,121n n n a a a --⎛⎫===⨯= ⎪⎝⎭，综上所述，()*54,14N 2,5n n n n a n n --≤≤⎧=∈⎨≥⎩；（2）当1m =时，1231236,6a a a a a a ++=-=-,满足条件；当2m =时，2342343,0a a a a a a ++=-=,不满足条件；当3m =时，3453450,0a a a a a a ++==，满足条件；当4m =时，4564562,0a a a a a a ++==,不满足条件；当5m ≥时，52n n a -=，若1212m m m m m m a a a a a a ++++++=,则有22111m m m m m m a a a a a a ++++++=,则5311222m m -+-++=，所以28722m -=，所以2727m -=，又因为273m -≥，所以2728m -≥，所以2727m -=无解，综上所述，m 的取值为{1,3}．16．（15分）【答案】（1）证明见解析；（2）3π【解析】（1）因为正方体1111ABCD A B C D -,所以四边形11ABB A 是正方形，所以11AB BA ⊥,又BC ⊥平面111,ABB A AB ⊂平面11ABB A ,所以1BC AB ⊥,又111,,AB BA BA BC ⊥是平面1A BC 内的两条相交直线，所以1AB ⊥面1A BC（2）如图，以A 为原点，以1,,AB AA AD 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系，设正方体1111ABCD A B C D -的边长为a ,又E 为线段1AC 的中点，则(0,0,0),(,0,0),(,,0),,,222a a a A B a C a a E ⎛⎫⎪⎝⎭，所以(,0,0),,,,(0,,0),,,222222a a a a a a AB a AE BC a BE ⎛⎫⎛⎫====- ⎪ ⎪⎝⎭⎝⎭，设平面ABE 的法向量为(,,)m x y z =,则0000222ax m AB a a ax y z m AE ⎧=⎧⋅=⎪⎪⇒⎨⎨++=⋅=⎪⎪⎩⎩,令1y =,则0,1x z ==-,所以(0,1,1)m =- ，设平面BCE 的法向量为()111,,n x y z =,11110000222ay n BC a a a x y z n BE ⎧=⎧⋅=⎪⎪⇒⎨⎨-++=⋅=⎪⎪⎩⎩，令1111,0x z y ===，所以(1,0,1)n = ，设平面ABE 与平面BCE 所成锐二面角的大小为θ．所以1cos ||||2m n m n θ⋅== ，又0,2πθ⎛⎫∈ ⎪⎝⎭，所以3πθ=17．（15分）【答案】（1）74；（2）0.8186；（3）分布列见解析；期望为65【解析】（1）根据频率分布直方图得：(550.01650.02750.045850.02950.005)1074x =⨯+⨯+⨯+⨯+⨯⨯=．（2）由题意知~(74,100)X N ,即74,10μσ==,所以0.68270.9545(6494)(2)0.81862P X P X μδμδ+<≤=-<≤+==．（3）由题意可知[50,60),[60,70)和[80,90)的频率之比为：1:2:2，故抽取的10人中[50,60),[60,70)和[80,90)分别为：2人，4人，4人，随机变量ξ的取值可以为0,1,2,3，321664331010C C C 11(0),(1)C 6C 2P P ξξ======，123644331010C C C 31(2),(3)C 10C 30P P ξξ======，故ξ的分布列为：ξ0123P1612310130所以11316()01236210305E ξ=⨯+⨯+⨯+⨯=．18．（17分）【答案】（1）221(2)43x y x +=≠-；（2）直线l 过定点．【解析】（1）设动圆P 的半径为r ,因为动圆P 与圆M 外切，所以||1PM r =+,因为动圆P 于圆N 外切，所以||3PN r =-,则||||(1)(3)4||2PM PN r r MN +=++-=>=,由椭圆的定义可知，曲线C 是以(1,0),(1,0)M N -为左、右焦点，长轴长为4的椭圆．设椭圆方程为22221(0)x y a b a b+=>>,则2,1a c ==,故2223b a c =-=,所以曲线C 的方程为221(2)43x y x +=≠-．（2）①当直线l斜率存在时，设直线:,l y kx m m =+≠联立22143x y y kx m ⎧+=⎪⎨⎪=+⎩，消去y 可得()()222438430k x kmx m +++-=，则()()222(8)164330km k m ∆=-+->,化简得22430k m -+>．设()()1122,,,A x y B x y ，则()12221228434343km x x k m x x k ⎧+=-⎪+⎪⎨-⎪=⎪+⎩．由题意可知，因为2QA QB k k +=-．2==-，所以)1221121220x y x y x x x x +-++=,所以()())1221121220x kx m x kx m x x x x +++++=,即()1212(22)(0k x x m x x ++-+=,()222438(22)(04343m km k m k k -⎛⎫+⋅+⋅-= ⎪++⎝⎭，即()2(1)3(0k m km m +--=,即(1)]0m m k -++=．因为m ≠，所以1)0m k +=,即m =所以直线l的方程为(y kx k x =-=-,所以直线l过定点．②当直线l 斜率不存在时，设直线:(0)l x t t =≠，且(2,2)t ∈-，则点,,A t B t ⎛⎛ ⎝⎝．所以k 2QA QBk k +=+==-,解得t =,所以直线l的方程为x =也过定点．综上所述，直线l过定点．19．（17分）【答案】（1）1y x =-（2）()f x 的单调递增区间是1,e⎛⎫+∞ ⎪⎝⎭；()f x 的单调递减区间是10,e ⎛⎫ ⎪⎝⎭（3）1a e ≥-．【解析】（1）因为函数()ln f x x x =,所以1()ln ln 1,(1)ln111f x x x x f x''=+⋅=+=+=．又因为(1)0f =,则切点坐标为(1,0)，所以曲线()y f x =在点(1,0)处的切线方程为1y x =-．（2）函数()ln f x x x =定义域为(0,)+∞,由（1）可知，()ln 1f x x '=+．令()0f x '=解得1x e=．()f x 与()f x '在区间(0,)+∞上的情况如下：x10,e ⎛⎫ ⎪⎝⎭1e1,e ⎛⎫+∞ ⎪⎝⎭()f x -0+()f x '↘极小值↗所以，()f x 的单调递增区间是1,e⎛⎫+∞ ⎪⎝⎭；()f x 的单调递减区间是10,e ⎛⎫⎪⎝⎭．（3）当1x e e ≤≤时，“()1f x ax ≤-”等价于“1ln a x x≥+”．令22111111()ln ,,,(),,x g x x x e g x x e x e x x x e -⎡⎤⎡⎤'=+∈=-=∈⎢⎥⎢⎥⎣⎦⎣⎦．令()0g x '=解得1x =,当1,1x e ⎛⎫∈ ⎪⎝⎭时，()0g x '<,所以()g x 在区间1,1e ⎛⎫ ⎪⎝⎭单调递减．当(1,)x e ∈时，()0g x '>,所以()g x 在区间(1,)e 单调递增．而111ln 1 1.5,()ln 1 1.5g e e e g e e e e e⎛⎫=+=->=+=+< ⎪⎝⎭．所以()g x 在区间1,e e ⎡⎤⎢⎥⎣⎦上的最大值为11g e e ⎛⎫=- ⎪⎝⎭．所以当1a e ≥-时，对于任意1,x e e⎡⎤∈⎢⎥⎣⎦,都有()1f x ax ≤-．。

四年级数学日记四年级数学日记（精选10篇）四年级上册数学日记18月13日星期四晴今天，我带了10元钱到好又多超市的3层楼去买书。

我找来找去找到了一本《神话传说》，一看封面就知道里面有许多精彩的故事。

我决定买下它，可一看定价，我又愣住了，原来这本书是11元。

我一边看着这本书，一边摸着口袋里的钱，可真叫我为难呀！售货员阿姨看到我为难的样子，亲切地问：“怎么了，小朋友？”我腼腆地说：“我想买这本书，可是钱不够。

”她又问：“你带了多少钱？”“只有10元。

”我说。

阿姨笑了笑说：“小朋友，你看定价牌上还写着‘优惠售书，一律九折’。

”我问：“什么叫‘一律九折’呀？”阿姨说：“就是按定价的十分之九收款，比如10元的书，只收9元。

”我算了算，这本书只要9元9角。

“对呀！”我连声向阿姨道谢。

今天，我既买到了满意的书，又学了知识，心里真高兴！四年级上册数学日记21月22日星期二天气：晴今天，妈妈给我出了一道盈亏问题：兔妈妈分配小白兔和小灰兔在几天里来摘一定数量的蘑菇。

小白兔计划前5天每天采80个，后几天每天采60个：小灰兔打算前三天每天采100个，后几天每天采70个，这样可以休息2天。

问小兔们应几天完成任务？各要采摘多少个蘑菇？我想了一想就做出来了：首先我把小白兔的计划转化成每天采60个，则少采：（80－60）5＝100（个）。

接着，我把小灰兔的计划转换成每天采70个，则多采：702－（100－70）3=50（个）。

然后按照盈亏问题的计算公式：份数=（盈＋亏）两次分配差计算出小兔们应（100＋50）（70－60）=15（天）完成任务。

最后用盈亏问题公式：总数量=每次分的数量份数+盈得出各要采805＋（15－5）60＝1000（个）蘑菇。

我把我的解题思路告诉妈妈，妈妈直夸我是个聪明的孩子，我的心乐滋滋的。

四年级上册数学日记39月11日星期日天气晴我正和妹妹玩得高兴，奶奶非把我叫去，让我给她算一笔账。

奶奶买了3斤4两的鸡蛋，每斤的价钱是3元5角，奶奶付了12元，应该找回多少钱？奶奶的话音刚落，爷爷就说道："找1角钱！"我不相信爷爷能算得这么快，便用我学过的数学知识进行计算：单价乘数量=总价；付出的.钱一花的钱=找回的钱，正好与爷爷的得数一样，找1角钱。

2022年人教版四4年级下册数学期末解答质量检测题附解析1．一个圆形花圃的面积是45公顷，里面种了4种不同的花，其中牡丹占总面积的310，百合占总面积的720，月季花占总面积的415，其余是玫瑰。

玫瑰占总面积的几分之几？2．某工程队修一条路，第一周修了全长的15，第二周修了全长的13，第三周比前两周修的总和少，少的部分占全长的415，第三周修了全长的几分之几？3．老师把45本书分给三个小组，第一组分得总数的35，第二组分得总数的13，剩下的分给第三组，第三组分得总数的几分之几？4．一节课的时间是40分钟，数学课上同学们做实验用了这节课的38，老师讲解用了这节课的49，其余时间同学们独立做作业。

同学们做作业用了这节课的几分之几？5．一支钢笔比一支圆珠笔贵6.5元，钢笔的单价是圆珠笔的3.5倍。

请你提出一个数学问题，并用方程解答。

6．同学们参观展览，五年级去的人数是四年级的1.6倍，比四年级去的人数多180人。

两个年级各去了多少人？7．学校举行书画竞赛，四、五年级共有75人获奖，其中五年级获奖人数是四年级的1.5倍，四、五年级各有多少同学获奖？（先写出等量关系，再列方程解答）8．某汽车销售公司去年第四季度售出小汽车和面包车共96辆。

这个公司去年第四季度销售小汽车和面包车各多少辆？（列方程解）9．明明和亮亮都到图书馆去借书，明明每6天去一次，亮亮每8天去一次，如果7月20日他们两人在图书馆相遇，那么下一次都到图书馆是几月几日？10．观察下面每个图形中小正方形的排列规律，并填空。

2＝1×22＋4＝2×32＋4＋6＝3×（）2＋4＋6＋8＝4×（）根据上面的规律用简便方法计算。

（1）2＋4＋6＋8＋10＋12＋14＋16＋18＋20（2）2＋4＋6＋ (2)11．花店挑选了15朵红花、25朵黄花搭配花篮，每篮两种花朵数分别相同，要使这些花刚好分完。

最多可以配多少篮？每篮至少有多少朵花？12．暑假期间，小林每6天游泳一次，小军每8天游泳一次。

暑假作业7月1日298×24= 447×42 = 315×48= 139×40= 408×25=210÷50= 277÷90= 330÷80= 310÷50= 250÷30=1、今年植树节，三年级植树360棵，是四年级的3倍。

三年级比四年级多植多少棵树？2、5人一小时加工零件135个，照这样计算，再增加4人，一小时一共加工多少个零件？7月2日217×46= 644×38= 646×13= 280×24= 409×12=380÷90= 325÷30= 435÷70= 222÷30= 248÷60=1、幼儿园买来苹果和梨各20箱，苹果每箱32千克，梨每箱25千克，买来的苹果比梨多多少千克？2、公园里有菊花100盆，比月季花少35盆，郁金香是菊花和月季花总数的3倍还多15盆。

公园里有郁金香多少盆？7月3日188×32= 415×26= 218×45= 130×55= 209×36=159÷30= 360÷50= 460÷60= 230÷30= 290÷70=1、王先生一家国庆期间自驾游，汽车每小时行驶65千米，他们上午9:00从家出发，下午1:00到达目的地，王先生家距离目的地有多少千米？2、王华看一本书，4天看了64页，照这样的速度，他再看5天才能看完，这本书一共有多少页？7月4日185×38= 524×18= 213×45= 170×86= 609×55=528÷69= 347÷52= 418÷48= 485÷62= 712÷80=1、超市新进8箱鸭蛋，每箱120只。

四年级暑假作业布置方案四年级暑假作业布置方案范文1）四年级暑假作业布置方案为了使学生渡过一个愉快而有意义的暑假，使他们在玩的同时不忘学习，特制定此假期计划。

一、安全方面：注意自身安全：不玩火，不到沟渠里游泳，不在有电线的地方玩，过马路注意交通安全，不在路上跑，不到危险的地方去，不能独自到人少的地方去，不听信陌生人的话。

一定要增强自我防范意识。

二、礼貌方面：现在你快是五年级的学生了，在家里要听父母的话，帮父母做一些力所能及的家务活，尊敬老人，爱护小孩子，讲话要文明，不说脏话。

三、习惯方面：每天安排好自己要做的事情，做作业要有计划，不要等到开学了才开始写作业。

合理安排好作息时间。

四、作业：数学：1、完成《暑假生活》。

2、调查一些生活用品的价格。

3、每天让父母出2道小数乘法和2道小数除法的计算题以及1道应用题。

4、每周出一份试卷。

5、看三本数学课外读物，拓展自己的知识面。

语文：1、完成《暑假生活》。

2、抄写生字，四字词语。

抄写20首古诗3、完成语文天地。

4、写10篇作文。

英语：每天写一个模块的单词，边写边读，一个单词5遍。

综合实践：1、调查小麦、玉米、水稻的种植成本，制作成统计表和统计图。

2、奥运专栏：形式有搜集和调查奥运知识、手抄报、剪贴报等。

2）小学四年级暑假作业前几天去母亲那里吃饭，看到妹妹手里拿着一本厚厚的练习题，一问才知道原来是小外甥的暑假作业。

这本书有近200页，16开大小，是一本《五年级数学天天练》，外甥刚刚上完小学4年级，却要去做五年级的题。

妹妹说，这本书只是所有作业的一小部分，我听了倒吸一口凉气。

我让妹妹把孩子抄写的作业项目给我抄了下来，具体如下：语文1、语文暑假作业一本，（16开大小，64页）2、每天记两个成语，每个词义读5遍，每个成语造一个句子3、每天抄两句名言警句、两句歇后语、两句谚语、两个对联。

4、每三天背诵并默写一首古诗。

5、小说《西游记》读完，里边的好词好句要重读。

6、写长篇小说15回，四天写一回，每回不少于800字。

初二数学证明试题1.如图，电路中有4个电阻和一个电流表A，若没有电流通过电流表A，问电阻器断路的可能情况共有种．【答案】8+3=11种【解析】要使没有电流通过电流表A，则若总路上的电阻是断开的，其它的三个电阻无论是断开，还是通的都可以，共有23=8种情况；若总路上的电阻是通的，则每一个支路都不能是通的，所以下面的电阻一定是断开的，上面的两个电阻只要有一个是断开的即可，有3种情况．故共有11种情况．解：本题分两种情况：①若主路的电阻不通，那么这个电路必为断路．因此共有2×2×2=8种可能；②若主路的电阻通电，那么两条支路必须同时为断路，因此共有3种可能．故电阻器断路的可能情况共有8+3=11种．点评：此题的学科综合性较强，能够结合物理中的知识进行分析求解是解答本题的关键．2.有一地球同步卫星A与地面四个科研机构B、C、D、E，它们两两之间可以互相接发信息，由于功率有限，卫星及每个科研机构都不能同时向两处发送信息（如A不能同时给B、C发信息，它可先发给B，再发给C），它们彼此之间一次接发信息的所需时间如右图所示．则一个信息由卫星发出到四个科研机构都接到该信息时所需的最短时间为．【答案】4【解析】首先卫星A传递信息给B用时1（秒），然后B传给C（3秒）；同时卫星传给E（1秒），信息传给D和C的时候同时进行，所有动作在4秒钟内结束．解：开始的时候，时间0秒，卫星传给B（1秒）第1秒钟时候，B传给C（3秒）；同时卫星传给E（1秒），第2秒钟的时候，E传给D，所有动作在4秒钟内结束，故接到该信息时所需的最短时间为4秒，故答案为4．点评：本题主要考查推理与论证的知识点，解答本题的关键是注意卫星传递信息的同时性，此题难度不大．3.暑假期间，小丽、小杰决定定期到敬老院打扫卫生，小丽每4天去一次，小杰每6天去一次，如果8月1日他们俩都在敬老院打扫卫生，那么，他们下一次同时在敬老院打扫卫生的时间是几月几日？【答案】8月13日【解析】根据4、6的最小公倍数是12，则他们每隔12天相遇一次，所以他们应在12天以后，即第13日再相遇．解：4、6的最小公倍数是12，所以他们应在12天以后，即第13日再相遇．答：他们下一次同时在敬老院打扫卫生的时间是8月13日．点评：本题主要是利用最小公倍数进行求解．4.有人认为数学没有多少使用价值，我们只要能数得清钞票，到菜场算得出价钱这点数学知识就够了．根据你学习数学的体会，谈谈你对数学这门学科的看法．【答案】见解析【解析】可以从数学的基础性，应用的广泛性，培养严密的逻辑思维能力，人文素养，科学精神等各方面价值作简单说明．解：答案不唯一，如：数学是思维的体操，可以培养自己的逻辑思维能力、发散思维能力等． 点评：此题为开放性试题，主要是考查学生对数学的认识．5. 推理能力都很强的甲、乙、丙站成一列，丙可以看见甲、乙，乙可以看见甲但看不见丙，甲看不见乙、丙．现有5顶帽子，3顶白色，2顶黑色．老师分别给每人戴上一顶帽子（在各自不知道的情况下）．老师先问丙是否知道头上的帽子颜色，丙回答说不知道；老师再问乙是否知道头上的帽子颜色，乙也回答说不知道；老师最后问甲是否知道头上的帽子颜色，甲回答说知道．请你说出甲戴了什么颜色的帽子，并写出推理过程． 【答案】见解析【解析】如果甲、乙都戴黑帽子，丙马上知道自己戴的是白帽子，如果甲戴黑帽子，甲、乙中至少有一个人戴白帽子，则乙马上知道自己戴的是白帽子． 解：甲戴的是白帽子．理由如下：因为丙说不知道，说明甲、乙中至少有一个人戴白帽子（如果甲、乙都戴黑帽子，丙马上知道自己戴的是白帽子）．因为乙也说不知道，说明甲戴的是白帽子（如果甲戴黑帽子，甲、乙中至少有一个人戴白帽子，则乙马上知道自己戴的是白帽子）．点评：本题主要考查了论证与推理的一些基础知识，能够找出题中的内在联系，从而求解．6. 10名棋手参加比赛，规定：每两名棋手间都要比赛一次，胜者得2分，下和各得1分，输者得0分．比赛结果表明：棋手们所得分数各不相同，前两名棋手没输过，前两名的总分之和比第三名多20分，第四名得分与后四名得分总和相等，那么前六名得分分别是多少？ 【答案】17，16，13，12，11，9【解析】先设第k 名选手的得分为a k （1≤k≤10），得出a 1、a 2的值，再根据得出a 4≥12，求出a 3，再根据a 1≤a 3﹣1=12，求出a 4，最后根据a 1+a 2+a 3+…a 8+a 9+a 10=90分别求出a 5、a 6的值．解：设第k 名选手的得分为a k （1≤k≤10），依题意得：a 1＞a 2＞a 3＞…a 9＞a 10a 1≤1+2×（9﹣1）=17，a 2≤a 1﹣1=16，a 3+20=a 1+a 2，∴a 3≤13 ①，又后四名棋手相互之间要比赛=6场，每场比赛双方的得分总和为2分，∴a 7+a 8+a 9+a 10≥12，∴a 4≥12而a 3≥a 4+1≥13，②∴由①②得：a 3=13，∴a 1+a 2=33，∴a 1=17，a 2=16，又∵a 1≤a 3﹣1=12，∴a 4=12， ∵a 1+a 2+a 3+…a 8+a 9+a 10=×2=90，∴17+16+13+12+a 5+a 6+12=90，而a 5+a 6≤a 5+a 5﹣1，即：a 5≥10\frac{1}{2}，又a5＜a 4=12， ∴a 5=11，a 6=9，故前六名得分分别是：17，16，13，12，11，9．点评：本题考查了推理与论证；解决问题的关键是读懂题意，找到所求的量的等量关系是解题的关键．7. 图中小圆圈表示网络的结点，结点之间的连接表示它们有网线相连，相连标注的数字表示该段网线单位时间内可以通过的最大信息量．现从结点A 向结点B 传递信息，若信息可以分开沿不同路线同时传递，则单位时间内传递的最大信息量为（ ）A ．11B ．10C ．8D ．7【答案】C【解析】先找出从结点A 向结点B 传递信息可沿A ﹣C ﹣B 和A ﹣D ﹣B 路线同时传递，再找出每条路线通过的最大信息量，然后相加即可得到答案．解：由于信息可以分开沿不同路线同时传递，所以从结点A 向结点B 传递信息可经过结点D 和结点B ；又因为从结点A 到结点D 的最大信息量为5，从结点C 到结点B 的最大信息量为3，所以从结点A 向结点B 传递信息，若信息可以分开沿不同路线同时传递，则单位时间内传递的最大信息量为5+3=8． 故选C ．点评：本题考查了推理与论证的方法：先分析题目所给的条件或要求，然后通过推理得到相关的结论．8. 如果甲的身高或体重数至少有一项比乙大，则称甲不亚于乙．在100个小伙子中，若某人不亚于其他99人，我们就称他为棒小伙子，那么100个小伙子中，棒小伙子最多可能有（ ） A ．1个 B ．2个 C ．50个 D ．100个【答案】D【解析】因为求得最多是多少人，且如果甲的身高或体重数至少有一项比乙大，我们可把这一百个小伙子用A 1～A 100来表示，然后根据体重和身高两个条件找出答案． 解：先退到两个小伙子的情形，如果 甲的身高数＞乙的身高数，且 乙的体重数＞甲的体重数 可知棒小伙子最多有2人． 再考虑三个小伙子的情形，如果甲的身高数＞乙的身高数＞丙的身高数，且 丙的体重数＞乙的体重数＞甲的体重数 可知棒小伙子最多有3人．这时就会体会出小伙子中的豆芽菜与胖墩现象．由此可以设想，当有100个小伙子时，设每个小伙子为A i ，（i=1，2，…，100），其身高数为x i ，体重数为y i ，当y 100＞y 99＞…＞y i ＞y i ﹣1＞…＞y 1且 x 1＞x 2＞…＞x i ＞x i+1＞…＞x 100时，由身高看，A i 不亚于A i+1，A i+2，…，A 100； 由体重看，A i 不亚于A i ﹣1，A i ﹣2，…，A 1所以，A i 不亚于其他99人（i=1，2，...，100） 所以，A i 为棒小伙子（i=1，2， (100)因此，100个小伙子中的棒小伙子最多可能有 100个． 故选D ．点评：本题考查推理和论证，关键注意本题有身高和体重两种情况，少有一项大，就称作不亚于，从而可求出解．9. 用1，2，3，4共可以写成不同的四位数（ ） A ．4个 B ．12个 C ．18个 D ．24个【答案】D【解析】当1作千位时，可得1234，1243，1324，1342，1423，1432，6个不同的四位数．同理可得其余3个数字当千位上的数字也会有6个不同的四位数，那么可以写成24个不同的四位数．解：当1作千位上的数字时，四位数可写成1234，1243，1324，1342，1423，1432共6个； 同理，当2、3、4作千位上的数字时，也分别可写成6个不同的四位数． 因此用1、2、3、4共可写成的不同四位数的个数为4×6=24．故选D ． 点评：解决本题应先找到确定一个数位上数的四位数的情况，进而得解．10.用锯锯木，锯会发热；用锉锉物，锉会发热；在石头上磨刀，刀会发热，所以物体摩擦会发热．此结论的得出运用的方法是（）A．观察B．实验C．归纳D．类比【答案】C【解析】由多种现象得到一个规律属于归纳．解：由多种现象得到一个规律属于归纳．故选C．点评：本题考查归纳的形成．所谓归纳，是指通过对特例的分析来引出普遍结论的一种推理形式．它由推理的前提和结论两部分构成：前提是若干已知的个别事实，是个别或特殊的判断、陈述，结论是从前提中通过推理而获得的猜想，是普遍性的陈述、判断．。

三年级北师大版上册数学应用题实验学校习题班级：__________ 姓名：__________1. 一列火车早上7：00从甲地出发，15：00到达乙地，这列火车共行驶了多长时间？2. 小红家有一个密码箱，其密码是由0至9中不同的四个数字组成的，由于疏忽，她只记住了后三位是365，那么小红要想打开箱子，最多需要试几次？3. 汤清杨和哥哥在开学时都买了一些作业本,如果哥哥给他3本的话,那么两个人的作业本数就一样多;如果汤清杨给哥哥1本的话,那么哥哥的本数就是他的3倍。

汤清杨和哥哥各买了多少本作业本?4. 修路队已经修路360米，还剩下未修的是已经修好的5倍。

这条路有多长？5. 兰兰读一本100页的故事书，每天读8页，她从8月11日开始读，能在8月21日读完这本故事书吗？6. 学校食堂王师傅买了 4 袋面粉，每袋面粉 118 元，他付给收银员一些钱后，收银员找给他 28 元，王师傅给的是多少钱？7. 明明和丽丽分别从相距220km的两地同时相向而行。

明明每小时行10km，丽丽每小时行12km，几小时后相遇？8. 一列火车每小时行驶125千米，早上8:00从昆明出发，中午11：00到丽江，昆明到丽江一共有多少千米？9. 某汽车厂计划全年生产汽车16800台，结果提前2个月就完成了全年的生产任务。

照这样的速度，全年可生产汽车多少台？10. 饲养场有黄牛和黑牛一共84头,黄牛卖掉20头后和黑牛同样多,饲养场原有黄牛和黑牛各多少头?11. 从甲地到乙地全长396千米，一辆汽车平均每小时行78千米，5小时能从甲地到达乙地吗？12. 每张成人票19元，买6张成人票大约要多少钱？13. 果园里今年收苹果728千克，收的梨是苹果的3倍，收梨多少千克？收苹果和梨一共多少千克？14. 图书馆购进一批少儿图书，其中《成语故事》72本，《寓言故事》比《成语故事》多18本。

《童话故事》的本数是《寓言故事》的3倍，购进《童话故事》多少本？15. 为庆祝“六·一”，学校大门旁边挂一排彩色气球，按照一个黄气球，两个红气球，三个绿气球的顺序排列。

人教五年级下册数学期末解答质量监测题（含解析）1．一台拖拉机耕一块地，上午耕了710公顷，下午比上午少耕了14公顷，全天一共耕地多少公顷？2．一台拖拉机耕一块地，上午耕78公顷，比下午多耕地14公顷。

这一天一共耕地多少公顷？3．一个圆形花圃的面积是45公顷，里面种了4种不同的花，其中牡丹占总面积的310，百合占总面积的720，月季花占总面积的415，其余是玫瑰。

玫瑰占总面积的几分之几？4．五（1）班同学去革命老区参观，共用去10小时，其中路上用去的时间占15，吃午饭与休息时间共占110，剩下的是游览时间，游览的时间占了几分之几？5．五年级有28名同学去植树，共植树104棵，其中男生每人植树5棵，女生每人植树3棵，参加植树的男、女生各有多少人？6．同学们参观“机器人”展览，四、五年级一共去了450人，五年级去的人数是四年级的1.5倍，两个年级各去了多少人？（列方程解答）7．实验小学举办“我最喜爱的电视节目”调查活动，喜欢小品和歌舞的观众共有700人，喜欢小品的人数是喜欢歌舞的2.5倍，喜欢小品和歌舞的各有多少人？（用方程解）8．有两桶油，甲桶油的质量是乙桶油的3倍，如果从甲桶中取出10千克油放入乙桶，两桶油的质量相等，两桶油原来各有多少千克？（用方程解）9．甲、乙两个小朋友爱去图书馆看书，甲每3天去一次，乙每4天去一次，8月1日两人在图书馆相遇，至少再过多少天两人能再次在图书馆相遇？是几月几日？10．暑假期间，小林每6天游泳一次，小军每8天游泳一次。

7月24日两人在游池相遇，八月几日他们再次相遇？11．把一张长32厘米、宽24厘米的长方形纸裁成同样大小、面积尽可能大的正方形，要求纸没有剩余。

至少可以裁出多少个？12．一座喷泉由内外双层构成。

外面每隔10分钟喷一次，里面每隔6分钟喷一次。

中午12：45同时喷过一次后，下次同时喷水是几时几分？13．“垃圾分类，从我做起”。

小玲家在上半年共收集“可回收垃圾”54.8kg，比“有害垃圾”重量的3倍还多0.5kg。

四年级数学暑期每天作业安排百惠学校7 月 5 号1.a 2和 2a 不行能相等。

（）2. 三角形的底扩大 5 倍，高减小 5 倍，面积不变。

（）3.3x － 8 不是方程。

（）4.周长相等的正方形 . 长方形 . 平行四边形中，平行四边形的面积最大。

（）5.104.104 读作一百零四点一百零四。

（）6.0.5 和 0.50 的大小相等，计数单位不一样。

（）7. 一个因数扩大 10 倍，另一个因数也扩大10 倍，本来的积就扩大20 倍。

（）8. 假如用 a 表示总价， b 表示单价， c 表示数目，那么 a = bc 。

（）9. 三角形的面积等于平行四边形面积的一半。

（）10.使方程左右两边相等的未知数的值叫解方程。

7 月 6 号1. 右图梯形ABCD的面积是60 平方厘米， E 是 AB的中点，三角形的面积是平方厘米。

（）① 40② 30③ 20④ 102. 下边不可以用1表示的是（）33. 如图，平行四边形的另一条高是厘米。

（）① 5 ② 10 ③ 11 ④ 124. 比 x 的 5 倍多 20 的数是（）① 5x = 20 ② 5x － 20 ③ 5x ＋ 20 ④ 20 － 5x1. 有三角形的花园，底是25 米，高是 22 米。

均匀每平方米产鲜花40 枝，这块花园一共可产鲜花多少枝？7 月 7 号3240÷ [24 ×（ 83－ 68） ]（680＋68× 45）÷ 55x÷ 36 = 17 4 x－5×8 = 201.24 除 192 的商加上 13，再乘以 11，积是多少？2. 什么数比 35 与 4 的积少 58？（用方程解。

）2. 小明在 60 米的跑道上走了4 次，第一次 152 步，第二次 155 步，第三次 145 步，第四次148 步。

他均匀每步走多少分米？7 月 8 号1. 比 1 小的最大两位小数是 ，它的计数单位是。

总复习测试卷(一)一、填空题。

(每题2分，共22分)1．一个数由8个百万，6个千，7个0.1和6个0.01组成，这个数写作( )，省略“万”位后面尾数约是( )。

2．45分：23时化成最简整数比是( )，比值是( )。

3．7.05吨＝( )吨( )千克 35分＝（ ）（ ）时4．（ ）12＝0.75＝( )÷20＝( )%＝( ):24＝( )折 5．57的分数单位是( )，再添上( )个这样的分数单位后是最小的质数。

6．三个连续奇数中间的数是m ，则m 的前面和后面的奇数分别是( )和( )。

7．如果a 和b 是不为0的两个连续自然数，那么a ，b 的最小公倍数是( )，最大公因数是( )。

8．57的后项加上21，要使比值不变，比的前项应加上( )。

9．根据规律填空。

12，23，35，58，813，( )，( )……10．今年植树节，六年级同学栽了180棵树，有20棵没有活，后来又补栽了20棵，全部成活。

六年级同学今年植树的成活率是( )。

11．40 kg 减少它的25后，再增加25 kg 是( )kg 。

二、判断题。

(每题1分，共6分)1．因为58>13，所以58的分数单位比13的分数单位大。

( ) 2．4900÷400＝49÷4＝12……1。

( ) 3．8和0.125互为倒数。

( ) 4．0.8和0.80大小相等，意义相同。

( ) 5．－2 ℃比－5 ℃的温度低。

( )6．把48%的百分号去掉，这个数就扩大为原来的100倍。

( ) 三、选择题。

(每题1分，共7分)1．下列分数中，不能化成有限小数的是( )。

A.720B.825C.712D.6152．六(1)班总人数一定，期中考试获得优秀的人数与优秀率( )。

A ．成正比例B ．成反比例C ．不成比例D ．无法确定3．两根同样长的绳子，甲绳用去14，乙绳用去14米，则两根绳子( )。

A ．甲剩下的长一些B ．乙剩下的长一些C ．甲、乙剩下的一样长D ．无法判断谁剩下的长4．在2.35·48·，2.3·548·，2.3548·，2.354·8·中，最小的数是( )。

计算题+解决问题8月1日1.计算下面各题，能简算的要简算。

237-73-27 1.25+2.36+3.75+4.6420.5-1.37-3.63 487-187-139-61102×17+98×17 138+560÷8×42.手工小组5人一共做了120件手工，平均每人做了多少件？3.一个等腰三角形的一个底角是30°，它的顶角是多少度？4.妈妈带了50元钱去超市买东西，买了一条毛巾15.7元，两把牙刷14.8元，还剩下多少元？9.85-4.3-1.7 25×365×458×101-58 12.36+9.6+3.64272-14×6÷3 9000÷（125×8）2.一本《童话故事》38.8元，一辆玩家小汽车16.8元，一本《童话故事》比一辆玩家小汽车贵多少元？3.学校购进1200本图书分给6个年级，每个年级有4个班。

平均每个班分到多少本图书？4.松鼠妈妈采松果，晴天每天可采20个，雨天每天可采12个，它接连8天一共采了112个松果，这8天中有几天是雨天？3.72+5.3+7.28+3.7 25.4-5.2-4.8256-127+144-173 7200÷25÷494×[128-(154-31)] 125×7×242.某地上周的最高气温分别是15℃、12℃、11℃、12℃、13℃、14℃、14℃，计算该地上周平均每天的最高气温。

3.一支钢笔的售价是一支铅笔的10倍，一个篮球的售价是一支铅笔的100倍。

一支钢笔售价9.00元，一支铅笔多少元？一个篮球多少元？4. 1吨小麦可以磨面粉0.83吨，100千克这种小麦可以磨面粉多少千克？4.28+1.69-1.28 706-57-1433.65-3.6+6.45-6.4 77×25×435×43+35×56+35 420+39÷13-1352.妈妈付电费用去45.4元，付水费用去3.8元，还剩14.6元，妈妈原来有多少元钱？3.地球的海洋面积约为3.61亿平方千米，约比陆地面积多2.12亿平方千米。

2024年人教版小学四4年级下册数学期末解答学业水平（含答案）1．如图：杨树：○○○○○○松树：○○○○○○○○○○○○（1）松树的棵数是杨树的几倍？（2）杨树的棵数是松树的几分之几？2．张爷爷种菜。

一块菜地的16种了黄瓜，36种了西红柿，剩下的种茄子，茄子占这块地的几分之几？3．某汽车公司生产线年产A品牌汽车18万台、B品牌汽车24万台，该汽车公司年产的A 品牌汽车占这两种汽车总量的几分之几？4．谁采茶速度快？5．一块瓷砖长60cm，宽45cm，至少要用多少块这样的瓷砖，才可以铺成一个正方形？6．8月份暑假期间，鹏鹏和甜甜去敬老院当志愿者照顾老人，他们去敬老院的日期各自有规律，（如下表○表示他们去的日子），两人下次相遇是几月几号？（写出必要的过程）7．一堆橘子，2个2个地拿正好拿完，3个3个地拿正好拿完，5个5个地拿正好拿完，这些橘子最少多少个？如果不超过200个，最多多少个？8．幼儿园的王老师买来了一些苹果，平均分给8位小朋友或10位小朋友，都正好能分完。

王老师至少买来多少个苹果？9．王叔叔是自行车运动爱好者，周末经常去训练场进行训练。

训练路线由三部分组成，从起点到全程的13处是上坡，从13处到全程的47处是下坡，其余的是平地，如下图所示。

（1）下坡路线占全程的几分之几？（2）王叔叔从起点出发，骑行了全程的310后原地休息，然后继续向终点方向骑行了全程的37，这时他处于哪段训练路线？（列式计算说明）10．一堂美术课，学生活动用了15小时，老师讲课用了310小时，其余的时间学生独立做画，学生独立做画用了多少小时？11．一瓶1升的饮料，小刚第一次喝了15升，第二次喝了14升。

小刚两次共喝了多少升饮料？12．五年①班的同学参加学校“数学文化节”活动，班上15的同学参加数独游戏，14的同学参加“24点”游戏，38的同学参加七巧板游戏。

其余的同学被老师选派担任文化节的工作人员。

（1）五年①班参加三项数学游戏的同学一共占了班上的几分之几？（2）五年①班担任文化节工作人员的同学占了班上的几分之几？（3）五年①班一共有40名同学，担任文化节工作人员的同学有几人？13．用一根长72厘米的铁丝围成一个长方体框架，长、宽、高的比是5∶3∶1，如果要给这个长方体框架表面糊上纸皮，至少需要多大面积的纸皮？14．一个油桶的形状是长方体，底面恰好是正方形，从里面量边长是4分米，深1米，做这个油桶至少需要多少平方分米的铁皮？桶内装的油占容积的34，如果每立方分米油重0.7千克，这个桶里的油有多少千克？15．一个美术教室长12米，宽8米，高3.5米。

期中复习计划日记8月12日今天开始进行期中复习计划，首先安排了数学的复习任务。

早上，我先复习了一遍数学的公式和定理，对于重点内容进行了归纳和总结。

下午，我选择了一些典型的例题进行练习，巩固了知识点的运用能力。

8月13日今天我继续进行英语的复习。

上午，我复习了英语语法的知识点，并进行了一些相关练习。

下午，我选择了一些听力材料进行听力练习，提高了自己的听力理解能力。

8月14日今天我进行了历史学科的复习。

早上，我复习了历史的重要事件和历史人物，加深了对历史的整体把握。

下午，我看了历史的教材，重点复习了一些重要章节，并做了一些相关的练习题。

8月15日今天我安排了语文的复习任务。

上午，我读了一些古代文学作品，加深了对文言文的理解。

下午，我进行了一些现代文学作品的阅读，提高了自己的阅读和鉴赏能力。

8月16日今天我进行了化学的复习。

上午，我复习了化学的基本概念和化学方程式的写法，加强了对化学知识的掌握。

下午，我进行了一些化学实验的模拟，提高了实验操作的能力。

8月17日今天我安排了物理学科的复习。

上午，我重点复习了力学和电磁学的知识点，并进行了一些相关的习题练习。

下午，我看了一些物理实验的视频资料，加深了对实验原理的理解。

8月18日今天我进行了地理的复习。

上午，我复习了地理的重要概念和地理要素的相互关系，加强了对地理知识的整体认知。

下午，我看了一些地理图谱，加深了对地理地形的认识。

8月19日今天我进行了生物学科的复习。

上午，我复习了生物的基本概念和生物进化的理论，加强了对生物知识的理解。

下午，我进行了一些实物的观察和实验，提高了自己的实验技能。

8月20日今天是最后一天的复习，我进行了综合的复习和总结。

上午，我回顾了每个学科的重点内容，并进行了一些综合题的练习。

下午，我做了一些模拟考试，检验了自己的复习成果。

8月21日今天是期中考试的第一天，我参加了数学和英语的考试。

我发现自己复习的内容基本都能答对，感到很满意。

绿豆芽观察日记集合15篇绿豆芽观察日记120__年 __月 __日周x9月的一天，我来到了一家书店。

在这里，我无意间看到了《在阳台上种菜》的这本书，看到了种绿豆芽。

什么种一次绿豆芽只要7天?不会吧，以前我种都要1个月!为了看这本书是否真实，我决定回家种一次看看。

经过了老妈的同意，我拿了10颗绿豆，按书上说的，盖了一块黑布泡了一些水，看了看我这些“可爱的”绿豆，心中不停地幻想着等我的小绿豆不断的长大、长大、长大、长大。

经过了一个漫长的夜晚，第二天早晨一起来，就直奔阳台，啊!我惊呆了，因为绿豆全都长大了，有的还长出了小芽呢!呆了一会儿，我才回过神来，赶紧把水倒掉，继续看着这些可爱的小苗成长。

又经过了漫长的第三天，第四天。

第五天。

到了第7天，小苗们个个都有15厘米高了，也都可以吃了，看来那本书说得一点也不假。

有一天，我抓一把绿豆放在一个小杯子里，杯子里装着半杯水，我放学回来时，看见水没有了，我想：一定是绿豆偷喝了。

第三天，我看见绿豆发了很小的芽，咧开口笑着，我也笑了。

我告诉妈妈可以炒一盘菜了，妈妈说：“豆芽太小了，再等一天吧!”第五天，放学回家我看到放在窗台的豆芽长得足够5厘米长，又光鲜又脆嫩，真是好看，用手一掐，都冒出水来。

妈妈把它做成了一道菜，真是一道好吃的菜。

绿豆芽观察日记2第三天，我格外高兴，你们猜为什么呢？因为今天我就可以吃到香喷喷的豆芽炒肉了！今天我一放学回到家，就掀起豆芽机上的遮光布，哇！“绿豆市民们”最大的已经长到大约八厘米了！其中有四厘米是伸到“豆芽床”下的小细根。

“豆芽床”上现在已经是拥挤不堪了！它们个个都吐着小舌头，都好像在对我喊着：“闷死了，闷死了！终于可以透口气了！”哦，我还要告诉你们一件事情，而且还是一件令人头疼的事情，你们猜怎么啦？其实呀就是“绿豆市民们”吵架了。

瞧！一群豆芽异口同声地对另一个豆芽说：“你为什么踩到我们的头上！”那个豆芽说：“喂！你们讲不讲道理呀！明明是你们把我挤到上面的嘛，我也没有办法呀！”话音刚落，那边又吵成了一锅粥！！！你们说这件事烦不烦人呀！还有一件令人高兴的事要告诉你们呢！下面那一层豆芽也不甘示弱呢！上面的绿豆芽的根须全都伸到了下面了，它们也不在乎，下层的“绿豆市民们”就像一个个“大力士”，把上层的“豆芽床”整个给托举起来了，你们说它们厉不厉害呢？我都好佩服它们呀！嘿嘿嘿，幸好它们想吵也吵不成了，想闹也闹不成了，因为它们马上就要变成我的盘中菜了！哈哈哈……生豆芽可真有意思！下次你们如果要生豆芽的话可一定要叫上我呦，我可是生豆芽的“专家”呢！绿豆芽观察日记38月13日是晴天从昨天种绿豆开始，就一直期待它发芽长大，但还是来得及的。

五年级上册数学小日记范文3篇五年级上册数学小日记范文3篇“铃铃铃”下课的铃声响了，同学们走出了教室。

我和张靖娜，邹诗瑶和杜鑫越在一起玩游戏——异想天开。

我们四个人一人拿出三块纸分别在纸上写出人物，地点，和做的什么事，写完之后把它们捏成一个小球，打乱顺序，分好堆，人物一堆，地点一堆，事情一堆，一人在三堆里拿出一个球，翻开并按照人物地点和事情连成一个句子。

我先读，郝教师在锅里抓鱼，哈哈哈，我们四个不由得笑出声来，张靖娜读，出雷宇航在电饭锅里洗澡。

哈哈哈，有一阵笑声，我插着腰撅着嘴看着张靖娜，扑哧一声笑了。

我们又恢复了刚刚的状态，这回到邹诗瑶了，她还没等说呢自己先笑上了，我们着急得对邹诗瑶说：快点。

邹诗瑶笑眯眯地说：杜鑫越在英语书上摘苹果。

杜鑫越边笑边看邹诗瑶，我有那么傻吗。

最后一个是杜鑫越：张靖娜在厕所里吃黑芝麻糊。

咦呀，我要吐了。

哈哈哈愉快地笑声给我们的校园添了几分色彩。

“铃铃铃”上课的铃声响起了我们拾掇好东西上了第二节课。

小学兴趣数学对小朋友数学学习才能的进步非常重要，同学们一定要多学多练。

为大家了数学日记：我的数学小实验，欢迎大家阅读。

今天中午，为了能把筷子体积测得更准确，我叫爸爸从化学室拿了一个细长的量筒，刻度单位更小，每个单位只有1立方厘米。

此时，我似乎感觉到了成功在向我招手，真可谓万事具备，只差动手实验了。

首先，我用铅笔在一次性筷子上划了一道分界限，将筷子平均分成两段，并用水浸泡，以免筷子在测定过程中洗水。

随后，将筷子插入量筒中，并用滴管将水滴入量筒中，让量筒内的水涨到筷子的分界限上，记下量筒内的水位刻度（38毫升）后，将筷子从量筒内取出，再记下量筒内的水位刻度（34。

5毫升），前后两次水位刻度之差就是这一部分筷子的体积，即3。

5立方厘米。

用同样的方法，我又测量了筷子另一部分的体积是5立方厘米，两次测定结果相加得到这双筷子的体积为8。

5立方厘米。

当我得到这个结果时，我兴奋地叫了，此时的我是多么自豪、多么骄傲啊！接着，我又按每人一天使用3双计算出了我们学校（1500人）及全国（12亿）一年消耗的一次性筷子量，分别是13。