数学实验作业

数学实验-作业1—及部分答案（要求：1. 每次上机课下课之前提交，文件名如：数学091朝鲁第一次作业.doc。

2. 交至邮箱：matlabzuoyetijiao@3.作业实行5分制，依次为A++，A+，A ，A-，A- -）4.作业中，需要编程实现的均要求列出你的代码，以及求解的结果）1.请上网或查阅各种资料并回答：MATLAB是什么？MATLAB能做什么？答：略2.请上网或查阅各种资料并回答：MATLAB语言突出的特点是什么？答：略3.在MATLAB软件中有几种获得帮助的途径？答：help函数，菜单栏help菜单。

4.请上网或查询MATLAB软件中inv函数的功能与特点。

答：用来求可逆矩阵的逆矩阵。

inv(A),即求已知矩阵A的逆矩阵。

5.请上网或查阅各种资料并回答：如何在MATLAB中建立向量和矩阵。

答：如在matlab中创建向量a=(2,-5,6,1);a=[2,-5,6,1];b= [2;-5;6;1];如在matlab中创建矩阵A=;A=[1,2,3;4,5,6;7,8,9]；A =1 2 34 5 67 8 96.请上网或查阅各种资料并回答：在MATLAB中，向量和矩阵如何进行基本加减乘除四则运算，以及矩阵的乘法。

答：a=[2,-5,6,1];b= [1,2,3,4];求向量的和与差，直接输入a+b,a-b,即可,当然必须要求两个向量大小一致。

如：>> a=[2,-5,6,1];b= [1,2,3,4];>> a+bans =3 -3 9 5>> a-b1 -7 3 -3>> a.*bans =2 -10 18 4>> a./bans =2.0000 -2.5000 2.0000 0.2500>> a/b向量之间进行除法运算，使用不加点的矩阵除法“A/B”时，问题可以描述为：给定两个向量A、B，求一个常量x，使得A=x * B。

数学实验之学生实验题目 MATLAB 简介实验一：数组操作及运算练习1．设有分块矩阵⎥⎦⎤⎢⎣⎡=⨯⨯⨯⨯22322333S O R E A ，其中E,R,O,S 分别为单位阵、随机阵、零阵和对角阵，试通过数值计算验证⎥⎦⎤⎢⎣⎡+=22S 0RS R EA 。

2．求如下非齐次线性方程组的通解，⎪⎩⎪⎨⎧=--+=+-+=+-+.12,2224,12w z y x w z y x w z y x3．某零售店有9种商品的单件进价（元）、售价（元）及一周的销量下表，问哪种商品的利润最大，哪种商品的利润最小；按收入由小到大，列出所有商品及其收入；求这一周该10种商品的总收入和总利润。

实验二：作图练习1. 用两种方法在同一个坐标下作出y 1= x 2,y 2= x 3,y 3= x 4 y 4= x 5这四条曲线的图形，并要求用两种方法在图上加各种标注。

2．用subplot 分别在不同的坐标系下作出下列四条曲线，为每幅图形加上标题， 1）概率曲线 2exy -=；2）四叶玫瑰线 r =sin2q ；3）叶形线 ⎪⎪⎩⎪⎪⎨⎧+=+=;13,13323t ty t t x 4）曳物线 22111lnyyy x --±= 。

3．作出下列曲面的3维图形，1）)sin(22y x z +=π；2）环面：⎪⎩⎪⎨⎧=+=+=,sin ,sin )cos 1(,cos )cos 1(u z v u y v u x )2,0()2,0(ππ∈∈v u 。

实验三：编写M-文件1．建立一个命令M-文件：求所有的“水仙花数”，所谓“水仙花数”是指一个三位数，其各位数字的立方和等于该数本身。

例如，153是一个水仙花数，因为153=13+53+33。

2．编写函数M-文件SQRT.m ：用迭代法求a x =的值。

求平方根的迭代公式为迭代的终止条件为前后两次求出的x 的差的绝对值小于10-5。

〈返回〉方程求解实验一：油价与船速的优化问题油价的上涨，将影响大型海船确定合理的航行速度，以优化航行收入。

八年级上册数学实践作业
一、活动目标：
1. 通过实践活动，使学生更加深入地理解和掌握基础的数学知识，提高数学的应用能力。

2. 通过小组合作，培养学生的团队协作精神和沟通能力。

3. 培养学生的创新思维和实践能力，提高他们解决问题的能力。

二、活动内容：
1. 分组调查：学生自由分组，每组4-6人。

选择一个与数学相关的话题进行调查研究，如“生活中的数学”、“数学在科学中的应用”等。

2. 数据收集：根据选定的话题，收集相关数据和信息。

可以通过网络、图书馆、实地调查等方式获取数据。

3. 数据整理：对收集到的数据进行整理，分类，以便于分析和解读。

4. 数据分析：运用所学的数学知识对数据进行处理和分析，发现其中的规律和趋势。

5. 报告撰写：将调查结果和数据分析写成报告，要求语言简洁明了，逻辑清晰。

6. 汇报展示：每组选派一名代表，向全班汇报展示本组的调查结果和分析。

三、活动要求：
1. 小组分工明确，每个成员都要积极参与调查和讨论。

2. 调查和分析过程中要尊重事实，严谨认真。

3. 报告要条理清晰，数据准确，分析深入。

4. 汇报时要自信流畅，能够清晰地表达本组的观点和结论。

四、活动时间安排：
1. 分组和选定话题（1周）
2. 数据收集（2周）
3. 数据整理和分析（1周）
4. 报告撰写（1周）
5. 汇报展示（1周）
五、评价标准：
1. 数据的准确性和完整性。

2. 分析的深入性和逻辑性。

3. 报告的条理性和可读性。

4. 小组的协作和沟通能力。

八年级数学生活实践作业
在数学的学习过程中，我们不仅要掌握基本概念、定理和方法，还要学会将数学知识应用到生活中。

为此，我们要开展数学生活实践作业。

一、数学游戏
通过数学游戏，可以在轻松愉快的氛围中巩固数学知识。

比如，猜数字、消除方块、九宫格等游戏，都可以锻炼我们的数学思维能力。

二、数学调查
通过数学调查，可以让我们了解周围的数学现象。

比如，调查同学们喜欢的运动项目及其比例，可以学习比例的概念和应用。

三、数学实验
通过数学实验，可以让我们亲身体验数学知识。

比如，用球体积和直径的关系验证球体积公式，可以帮助我们理解和记忆公式。

四、数学应用
通过数学应用，可以让我们将数学知识应用到实际生活中。

比如，设计平面图、制作尺子、计算面积和周长等活动，都可以培养我们的数学应用能力。

五、数学探究
通过数学探究，可以让我们自主发现数学规律和性质。

比如，探究数列的规律、研究数学模型等活动，都可以培养我们的数学思维和创新能力。

六、数学竞赛
通过数学竞赛，可以让我们在比赛中巩固和提高数学知识。

比如，参加奥数、数学建模等比赛，可以锻炼我们的数学能力和竞赛意识。

总之，数学生活实践作业是数学学习的重要组成部分。

希望同学们能够积极参与，将数学知识与生活实践结合起来，提高自己的数学素养。

小学生数学实验100例第1篇：我的数学小实验的日记今天中午，为了能把筷子体积测得更准确，我叫爸爸从化学室拿了一个细长的量筒，刻度单位更小，每个单位只有1立方厘米。

此时，我似乎感觉到了胜利在向我招手，真可谓万事具备，只差动手实验了。

首先，我用铅笔在一次筷子上划了一道分界线，将筷子平均分成两段，并用水浸泡，以免筷子在测定过程中洗水。

随后，将筷子入量筒中，并用滴管将水滴入量筒中，让量筒内的水涨到筷子的分界线上，记下量筒内的水位刻度（38毫升）后，将筷子从量筒内取出，再记下量筒内的水位刻度（34.5毫升），前后两次水位刻度之差就是这一部分筷子的体积，即3.5立方厘米。

用同样的方法，我又测量了筷子另一部分的体积是5立方厘米，两次测定结果相加得到这双筷子的体积为8.5立方厘米。

当我得到这个结果时，我兴奋地叫了，此时的我是多么自豪、多么骄傲啊！接着，我又按每人一天使用3双计算出了我们学校（1500人）及全国（12亿）一年消耗的一次*筷子量，分别是13.96立方米和11169000立方米。

结果使我大吃一惊，每年竟有这么多的木料做成一次筷子被浪费了，真是太可惜！在此，我呼吁在校的同学，不！是全国，也不！应该是全世界的每个人都不要再使用一次筷子了，只有这样，才能保护好我们的森林资源，使我们共有的地球环境更加美好，让地球上的每一个人呼吸到干净、清新的空气。

第2篇：我的小实验数学日记下午放学时，班主任老师给我们布置了一道家庭作业，要求大家想办法测算一次筷子的体积，并用数学日记的形式将测算过程记录下来。

这道家庭作业，表面上是一次数学实践活动，实际可能寓意更深，因为一次筷子的使用与环保有关，一回到家，我就静静地坐在书桌前思考这个问题。

一次*筷子的形状是一个不规则的立体图形，怎样才能测算出它的体积呢?我思来想去，一会儿抓耳挠腮，一会儿摇，终于，有了一点眉目。

我可以将一次筷子放入装满水的容器中，这样容器中的水就会溢出来，溢出水的多少不就是筷子的体积吗?可是筷子比水轻，会浮在水面上，又该怎么办呢?可不可以用石头或胶布之类的东西将筷子固定住呢?我想应该是可以的，但这些办法测定起来又都太麻烦了，要是有更简便的方法该多好啊!经过冥思苦想，我终于自豪的笑了。

第1篇一、作业背景随着我国基础教育改革的不断深入，数学教学教研工作越来越受到重视。

为了提高数学教学质量，促进教师专业成长，我们学校开展了数学教学教研实践活动。

本次实践作业旨在通过教师间的合作、研讨和反思，提升数学教学水平，培养学生的数学素养。

二、作业目标1. 提高教师对数学教学的理解和认识，掌握数学教学的基本规律和教学方法。

2. 培养教师之间的合作意识，促进教师间的交流与学习。

3. 提升教师的教学设计能力，优化教学过程，提高教学质量。

4. 培养学生的数学思维能力、逻辑思维能力和创新能力。

三、作业内容1. 教学观摩与反思（1）观摩：选择一节数学课，进行全程观摩，记录下课堂中的亮点和不足。

（2）反思：结合观摩内容，从教学目标、教学内容、教学方法、教学评价等方面进行反思，总结经验教训。

2. 教学研讨与交流（1）主题研讨：围绕一个具体的教学问题，如“如何培养学生的数学思维能力”，组织教师进行研讨。

（2）经验分享：教师们分享自己在教学过程中的成功经验和做法，互相借鉴，共同提高。

3. 教学设计与实践（1）设计：根据教学目标和教学内容，设计一节数学课的教学方案。

（2）实践：在课堂上实施教学方案，观察学生的学习效果，并根据实际情况进行调整。

4. 教学评价与反馈（1）评价：对教学设计、教学过程和学生学习效果进行评价。

（2）反馈：根据评价结果，对教学方案进行改进，提高教学质量。

四、作业实施步骤1. 制定计划：根据学校教学教研计划，确定实践作业的具体内容和时间安排。

2. 组织实施：按照计划，组织教师开展各项实践活动。

3. 汇报交流：教师完成实践作业后，进行汇报交流，分享经验，互相学习。

4. 总结反思：对实践作业进行总结，分析存在的问题和不足，提出改进措施。

五、作业成果展示1. 教学案例集：收集教师在实践过程中积累的优秀教学案例，汇编成册。

2. 教学论文集：教师撰写教学论文，总结实践经验，提高教育教学理论水平。

3. 教学公开课：组织教师开展公开课活动，展示实践成果，促进教师间的交流与合作。

二年级数学创意实践作业
1. 数学游戏设计，让学生设计一个简单的数学游戏，例如数学拼图、数学迷宫等。

他们可以使用基本的加减法来设计游戏规则，并与同学们分享他们的游戏。

2. 数学手工制作，让学生使用纸板、彩纸等材料制作一些数学教具，例如数字卡片、几何图形模型等。

通过动手制作，学生可以更好地理解数学概念。

3. 数学故事创作，鼓励学生编写一个关于数学的小故事，可以是关于数字的奇妙故事，也可以是关于解决数学问题的故事。

这样的创作可以培养学生的想象力和逻辑思维能力。

4. 数学实地探索，组织学生到校园或社区进行数学实地探索，例如数数树上的鸟巢、测量操场的长度和宽度等。

通过实地探索，学生能够将抽象的数学概念与日常生活联系起来。

5. 数学竞赛活动，组织一个小型的数学竞赛，让学生在游戏中巩固所学的数学知识，激发他们的学习兴趣和竞争意识。

这些创意实践作业可以帮助学生在实践中感受到数学的乐趣，提高他们的动手能力和逻辑思维能力，同时巩固所学的数学知识。

希望这些建议能对你有所帮助。

一、作业目的通过本次暑假数学实践作业，帮助学生巩固和运用二年级上学期的数学知识，提高学生的数学思维能力、实践能力和创新能力。

同时，培养学生良好的学习习惯，激发学生对数学学习的兴趣。

二、作业内容1. 实践活动一：生活中的数学（1）观察和记录：请家长带领学生观察和记录生活中常见的数学现象，如：商品的标价、购物时的计算、家庭用电量等。

（2）分析：引导学生分析这些现象背后的数学原理，如：整数、小数的加减乘除运算。

（3）作业：请学生选择其中一个现象，用文字、图画或表格等形式记录下来，并简要说明其数学原理。

2. 实践活动二：数学游戏（1）制作数学游戏：学生可以和家长一起制作一些简单的数学游戏，如：数独、找规律等。

（2）游戏规则：制定游戏规则，确保游戏的公平性和趣味性。

（3）作业：请学生介绍自己制作的数学游戏，包括游戏名称、规则和玩法。

3. 实践活动三：数学日记（1）记录生活：学生每天记录生活中遇到的数学问题，如：购物、旅游、做家务等。

（2）思考与解答：针对记录的问题，引导学生运用所学数学知识进行思考和解答。

（3）作业：请学生选择一个具有代表性的数学问题，用文字、图画或表格等形式记录下来，并说明解题思路。

4. 实践活动四：数学实验（1）实验材料：准备一些简单的实验材料，如：水、杯子、橡皮筋等。

（2）实验过程：根据实验材料，设计一个有趣的数学实验，如：探究水杯容积、观察橡皮筋的弹性等。

（3）作业：请学生详细记录实验过程，包括实验步骤、实验现象和实验结论。

5. 实践活动五：数学故事（1）收集素材：引导学生收集关于数学家的故事，如：陈景润、华罗庚等。

（2）编写故事：根据收集到的素材，编写一个数学故事。

（3）作业：请学生讲述自己编写的数学故事，并简要介绍故事中的数学知识。

6. 实践活动六：数学绘画（1）主题选择：学生可以选择自己感兴趣的数学主题，如：几何图形、数学符号等。

（2）绘画创作：根据主题，进行绘画创作。

（3）作业：请学生展示自己的绘画作品，并简要介绍作品中的数学元素。

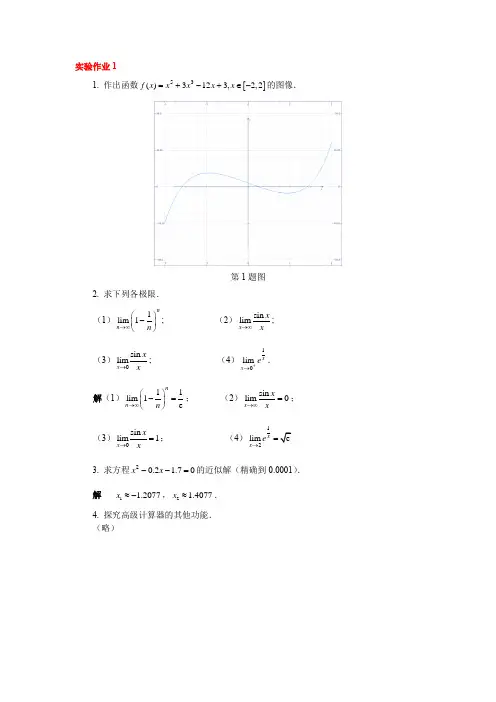
1. 作出函数[]53()3123,2,2f x x x x x =+-+∈-的图像．第1题图2. 求下列各极限．（1）1lim 1nn n →∞⎛⎫- ⎪⎝⎭; （2）sin lim x x x →∞;（3）0sin lim x x x →; （4）10lim x x e +→．解（1）11lim 1enn n →∞⎛⎫-= ⎪⎝⎭； （2）sin lim 0x x x →∞=；（3）0sin lim 1x xx →=； （4）12lim e x x e →3. 求方程20.2 1.70x x --=的近似解（精确到0.0001）． 解 1 1.2077x ≈-，2 1.4077x ≈． 4. 探究高级计算器的其他功能．（略）1. 求函数3(21)y x x =-的导数； 操作：在命令窗口中输入：>> syms xy=x^3*(2*x -1); dy=diff(y) 按Enter 键，显示：dy = 3*x^2*(2*x -1)+2*x^3 继续输入：>> simplify(dy) % 将导数化简 按Enter 键，显示： ans =8*x^3-3*x^2即 3283y x x '=-． 2. 求函数()ln 1y x x =-+的二阶导数； 操作：在命令窗口中输入： >> syms xy=1-log(1+x); dy=diff(y,x,2) 按Enter 键，显示： dy = 1/(1+x)^2即 21(1)y x ''=+． 3.函数4322341y x x x x =-+-+在区间[-3,2]上的最小值． 操作：在命令窗口中输入：>>x=fminbnd('x^4-2*x^3+3*x^2-4*x+1',-3,2) y=x^4-2*x^3+3*x^2-4*x+1 按Enter 键，显示： x =1 y =-11．求下列不定积分（1）在命令窗口中输入： >> syms xint(x/(sqrt(x^2+1)),x)按键Enter 键，显示结果： ans = (x^2+1)^(1/2)即c +.（2）在命令窗口中输入： >> syms xint(x^3*cos(x))按键Enter 键，显示结果：ans =x^3*sin(x)+3*x^2*cos(x)-6*cos(x)-6*x*sin(x) 即332cos =sin 3cos 6cos 6sin x xdx x x x x x x x c +--+⎰. 2．求下列定积分（1）在命令窗口中输入： >> int((-3*x+2)^10,x,0,1) 点击Enter 键，显示结果： ans = 683/11 即1100683(-3+2)d =11x x ⎰. （2）在命令窗口中输入： >> int(x*sin(x),x,0,pi/2)点击Enter 键，显示结果： ans = 1 即 π20sin d =1x x x ⎰.3．求广义积分0e d x x x -∞⎰.操作：在命令窗口中输入： >>int(x*exp(x),x,-inf,0)按Enter 键，显示结果： ans =-1 即e d =1xx x -∞-⎰.1. 230y y y '''++=.操作：在命令窗口中输入： >> syms x y;y=dsolve('D2y -4*Dy -5*y=0','x') 显示：y =C1*exp(5*x)+C2*exp(-x)即满足所给初始条件的特解为：512xx y c e c e -=-．2. 232sin xy y e x '''-=.操作：在命令窗口中输入： >> syms x y;y=dsolve('D2y -3*Dy=2*exp(3*x)*sin(x)','x') 显示：y = -3/5*exp(3*x)*cos(x)-1/5*exp(3*x)*sin(x)+1/3*exp(x)^3*C1+C2即满足所给初始条件的特解为：33312311cos sin 553xxxy e x e x c e c =--++． 整理得：33213cos +sin 5xxy e x x ce c =-++（）（令113c c =）3. +cos x y y y e x '''+=+，00x y ==，032x y ='=.操作：在命令窗口中输入： >> syms x y;y=dsolve('D2y+Dy+y=exp(x)+cos(x)','y(0)=0', 'Dy(0)=3/2', 'x') 显示：y = -1/3*exp(-1/2*x)*cos(1/2*3^(1/2)*x)+1/3*exp(x)+sin(x)即满足所给初始条件的特解为：211cos()sin 323x xy e e x -=-++．1. 绘制平面曲线ln y x =． 操作：在命令窗口中输入： >> x=1:0.02: exp(2); y=log(x); plot(x,y);按Enter 键，显示下图：2. 绘制空间曲面2232z x y =-. 操作：在命令窗口输入 >>[x,y]=meshgrid(-4:0.5:4); z=-3*x.^2-2*y.^2; surf(x,y,z)按Enter 键，显示下图：3. 绘制空间曲线23,23.t t t x e y e z e ---⎧=⎪⎪=⎨⎪=⎪⎩操作：在命令窗口输入>>t=0:0.01:1;x=exp(-t);y=exp(-2*t)/4;z=3*exp(-3*t)/9;plot3(x,y,z)按Enter键，显示下图：实验6作业题1. 求函数cos z xy =的偏导数. 操作：在命令窗口中输入：>> dz_dx=diff('cos(x*y)', 'x ') 显示dz_dx = -sin(x*y)*y 继续输入：>> dz_dy=diff('cos(x*y)', 'y ') 显示：dz_dy =-sin(x*y)*x即sin zx xy x∂=-∂， sin z x xy y ∂=-∂2. 计算函数23y x y =-的极值.操作：在matlab 中依次选择“File\New\M -File ”，在弹出的M 文件编辑窗口中在命令窗口中输入：clear all;clc syms x y;z=x^3-6*x-y^3+3*y;dz_dx=diff(z,x); %计算z 对x 的偏导数 dz_dy=diff(z,y); %计算z 对y 的偏导数 [x0,y0]=solve(dz_dx,dz_dy); %求驻点x0,y0A_=diff(z,x,2); %计算z 对x 的二阶偏导数B_=diff(diff(z,x),y); %计算z 对x,y 的二阶混合偏导数 C_=diff(z,y,2); %计算z 对y 的二阶偏导数 x0=double(x0); %数据转换 y0=double(y0);n=length(x0); %计算x0中元素的个数 for i=1:nA_x=subs(A_, x,x0(i)); %把x=x0(i)(即x0的第i 个元素值)代入z 对x 的二阶偏导数A=subs(A_x, y,y0(i)); %继续把y=y0(i)(即y0的第i 个元素值)代入z 对x 的二阶偏导数,得到AB_x=subs(B_, x,x0(i)); %把x=x0(i)代入z 对x 、y 的二阶混合偏导数 B=subs(B_x, y,y0(i)); %继续把y=y0(i)代入二阶混合偏导数,得到B C_x=subs(C_, x,x0(i)); %把x=x0(i)代入z 对y 的二阶偏导数C=subs(C_x, y,y0(i)); %继续把y=y0(i)代入z 对y 的二阶偏导数，得到C D=A*C-B^2;text=['原函数在(',num2str(x0(i)), ', ',num2str(y0(i)), ')处' ]; if D>0fm=subs(x^3-6*x-y^3+3*y,{x,y},{x0(i),y0(i)}); %求函数值 if A>0disp([text, '有极小值',num2str(fm)]) %在命令窗口中输出 elsedisp([text, '有极大值',num2str(fm)])end end if D==0disp([text, '的极值情况还不确定，还需另作讨论' ]) end end保存后，选择M 文件编辑窗口中的“Debug\run ”，显示如下结果： 原函数在(1.4142,-1)处有极小值-7.6569 原函数在(-1.4142,1)处有极大值7.65693. 计算(2)d d Dx y x y -⎰⎰，D ：顶点分别为(0,0)，(1,1)和(0,1)的三角形闭区域；操作：在命令窗口中输入： >>syms x y;S=int(int(2*x-y,y,0,1-x),x,0,1) 显示： S=1/6即：二重积分1(2)d d =6Dx y x y -⎰⎰.实验7作业题1. 将函数xx f -=11)(展开为幂级数，写出展开至6次幂项. 操作：在命令窗口中输入： >> clear;clc syms x; f=1/(1-2*x); taylor(f,7,x) 显示：ans = 1+2*x+4*x^2+8*x^3+16*x^4+32*x^5+64*x^6即65432643216842111x x x x x x x ++++++=-. 2. 求函数2()tf t e =的拉氏变换.操作：在命令窗口中输入： >> clear;clc syms x;laplace(exp(2*t)) 显示： ans = 1/(s -2)即 21)(2-=s e L t. 3.求函数22()56s F s s s +=-+的拉氏逆变换.操作：在命令窗口中输入： >>syms silaplace((s+2)/(s^2-5*s+6)) 显示：ans =-4*exp(2*t)+5*exp(3*t)即 12256s L s s -+⎡⎤⎢⎥-+⎣⎦234e 5e t t =-+.。

（1）产生一个5阶魔方矩阵M：M=magic(5)（2）将矩阵M的第3行4列元素赋值给变量t：t=M(3,4)（3）将由矩阵M第2，3，4行第2,5列构成的子矩阵赋给变N：N=M(2:4,2:3:5)（4）将由矩阵M的前3行赋给变量N：N=M(1:3,:)（5）将由矩阵M的后3列赋给变量N：N=M(:,end:-1:end-2)（6）提取M的主对角线元素，并以这些对角线元素构成对角矩阵N：N=diag(diag(M))或N=tril(triu(M)) (7)随机产生1000个100以内的整数赋值给变量t：t=round(rand(1,1000)*100)（8）随机产生100*5个100以内的实数赋值给变量M：M=rand(100,5)*100（1）删除矩阵M的第7个元素M(7)=[]（2）将含有12个元素的向量t转换成3*4的矩阵：reshape(t,3,4)（3）产生和M同样大小的单位矩阵：eye(size(M))（4）寻找向量t中非零元素的下标：find(t)（5）逆序显示向量t中的元素：t(end:-1:1)（6）显示向量t偶数位置上的元素：t(2:2:end)（7）利用find函数，将向量t中小于10的整数置为0：t(find(t<10&rem(t,1)==0))=0（8）不用find函数，将向量t中小于10的整数置为0：t(t<10&rem(t,1)==0)=0（9）将向量t中的0元素用机器0（realmin）来代替：t(find(t=0))=realmin（10）将矩阵M中小于10的整数置为0：M(find(M<10)&rem(M,1)==0)=02、写出完成下列操作的命令及结果。

（1）将1~50这50个整数按行优先存放到5*10的矩阵中，求该矩阵四周元素的和；>> t=[1:10];>> M=[t;t+10;t+20;t+30;t+40]M =1 2 3 4 5 6 7 8 9 1011 12 13 14 15 16 17 18 19 2 021 22 23 24 25 26 27 28 29 3 031 32 33 34 35 36 37 38 39 4 041 42 43 44 45 46 47 48 49 5 0>> N=M(2:4,2:9)N =12 13 14 15 16 17 18 1922 23 24 25 26 27 28 2932 33 34 35 36 37 38 39>> sum(sum(M))-sum(sum(n))ans =6632）n取100、1000、10000，求序列1、1/2、1/3……1/n的和。

四年级数学滴水实验练习题滴水实验是一种常见的数学实验，通过该实验可以帮助学生直观地理解数的增加和减少。

下面是一些关于滴水实验的练习题，帮助四年级学生巩固对数的概念和运算的理解。

1. 小明在滴水实验中，先往容器中滴入5滴水，接着又滴入3滴水。

请问容器里共有几滴水？2. 小红在滴水实验中，先往容器中滴入7滴水，接着又滴入2滴水，然后又滴入5滴水。

请问容器里共有几滴水？3. 小华在滴水实验中，先往容器中滴入4滴水，接着又滴入6滴水，然后再滴入3滴水。

请问容器里共有几滴水？4. 小明在滴水实验中，先往容器中滴入10滴水，接着每次都滴入2滴水，滴了5次。

请问容器里共有几滴水？5. 小红在滴水实验中，先往容器中滴入8滴水，接着每次都滴入3滴水，滴了4次。

请问容器里共有几滴水？解答：1. 小明一共滴入5滴水，再滴入3滴水，所以容器中共有5 + 3 = 8滴水。

2. 小红一共滴入7滴水，再滴入2滴水，最后滴入5滴水，所以容器中共有7 + 2 + 5 = 14滴水。

3. 小华一共滴入4滴水，再滴入6滴水，最后滴入3滴水，所以容器中共有4 + 6 + 3 = 13滴水。

4. 小明先滴入10滴水，然后每次都滴入2滴水，滴了5次，所以容器中共有10 + 2×5 = 10 + 10 = 20滴水。

5. 小红先滴入8滴水，然后每次都滴入3滴水，滴了4次，所以容器中共有8 + 3×4 = 8 + 12 = 20滴水。

通过这些练习题，我们可以观察到在滴水实验中，数的增加可以通过加法来表示，而数的减少可以通过减法来表示。

希望同学们通过这个实验，能够更好地理解和掌握数的增加和减少的概念，从而在数学学习中更加自信和熟练。

数学实验作业七题目：P200. 2)；6) 日期：2003-4-9【实验目的】：1、掌握MATLAB 优化工具箱的基本用法，对不同算法进行初步分析、比较。

2、练习实际问题的非线性最小二乘拟合。

【实验内容】：二：求解()12212122min 42421x e x x x x x ++++，初值（－1，1），对不同算法的结果进行分析、比较。

【模型分析】：首先画出函数f=12212122(42421)x e x x x x x ++++的图像和等高线：可以看到：在[0.5,-1]附近为一个“凹地”，最小值应在该凹地中取得。

另外，从（-1,1）到此凹地为一与Rosenbrock 函数类似的狭长通道，不利于沿负梯度方向下降。

可以想象，该函数具有与Rosenbrock 函数类似的性质。

【MATLAB 源程序】比较程序如下：%数学实验作业二.1-dfunction f=ch72fun(x);%第7章第2题的函数f=exp(x(1)).*(4*x(1).^2+2*x(2).^2+4*x(1).*x(2)+2.*x(2)+1);%ch72.m%第7章第2题X0=[-1,1];%赋初值%BFGS,混合二三次插值opt1=optimset('TolX',1e-6,'TolFun',1e-6,'MaxIter',1000);[X1,FV AL,EXITFLAG,OUTPUT]=FMINUNC(@ch72fun,X0,opt1)%BFGS,三次插值opt2=optimset(opt1,'LineSearchType','cubicpoly');[X1,FV AL,EXITFLAG,OUTPUT]=FMINUNC(@ch72fun,X0,opt2)%DFP,混合二三次插值opt3=optimset(opt1,'HessUpdate','dfp');[X1,FV AL,EXITFLAG,OUTPUT]=FMINUNC(@ch72fun,X0,opt3)%DFP,三次插值opt4=optimset(opt3,'LineSearchType','cubicpoly');[X1,FV AL,EXITFLAG,OUTPUT]=FMINUNC(@ch72fun,X0,opt4)%最速下降,混合二三次插值opt5=optimset(opt1,'HessUpdate','steepdesc');[X1,FV AL,EXITFLAG,OUTPUT]=FMINUNC(@ch72fun,X0,opt5)【MATLAB 运行结果】：结果为：所以可以得到本题的解析解：x=(0.5,-1)，f=0。

50个简单的数学小实验1. 滚动骰子，记录每个点数的数量，进行统计分析。

2. 观察不同颜色的薯片在水中的沉浮情况，研究密度与沉浮关系。

3. 使用不同比例的液体混合，观察颜色的变化。

4. 抛掷硬币，记录正反面的次数，进行概率分析。

5. 用尺子测量不同物品的长度、宽度和高度，并计算体积。

6. 研究太阳光的折射现象，观察镜面反射和散射。

7. 测量水的密度，并探究不同温度下密度的变化。

8. 按照不同比例混合物质制作彩色火焰，观察颜色的变化。

9. 观察火柴棒在水中的漂浮情况，探究密度与沉浮关系。

10. 测量不同颜色纸张的吸光度，并研究颜色与吸光度的关系。

11. 投掷骰子，计算点数之和的概率分布。

12. 测量不同材质的物体上的摩擦系数，并计算摩擦力。

13. 研究声音的传播和反射，观察声波在不同介质中的特性。

14. 制作简易水银温度计，测量温度的变化。

15. 用万能表测量不同电器的电阻、电流和电压。

16. 研究气体的扩散速率，观察气体分子在不同温度下的运动状态。

17. 测量不同颜色光线的波长和频率，并探究颜色与波长频率的关系。

18. 使用不同硬度的铅笔在不同纸张上写字，观察痕迹的深浅和清晰度。

19. 用扫描电镜观察不同物质的微观结构，并比较不同物质之间的差异。

20. 研究磁场的强度和方向，探究电流与磁场的相互作用关系。

21. 设计和制作简易的电磁铁，测量其磁场强度和电阻。

22. 投掷飞镖，研究飞行轨迹和命中准确度。

23. 测量不同物体的密度，计算质量和体积的比值。

24. 制作水晶，观察不同溶液的晶体形态和颜色。

25. 研究不同材质之间的传热过程，探究热传导和热辐射的特性。

26. 测量不同物体的电荷量，研究电荷与电力的相互作用关系。

27. 观察不同金属的折射率和反射率，研究光的特性在金属中的表现。

28. 测量不同水平面上的液体压力和重力，探究液体压力和重力的关系。

29. 研究不同状态的气体压强，探究气体压强与体积的关系。

六年级数学实践作业
六年级数学实践作业示例：
题目：测量并计算家中常见物品的面积或体积
目标：通过实际操作，加深对面积和体积计算的理解，提高数学应用能力。

步骤：
1. 选择家中常见的物品，例如：餐桌、电视机、书柜、水桶等。

2. 使用测量工具（如卷尺）测量所选物品的长、宽、高。

3. 根据测量数据，使用面积和体积的计算公式（面积=长×宽，体积=长×宽×高），计算所选物品的面积和体积。

4. 将测量数据、计算过程和结果记录在实践作业表格中。

5. 分析测量和计算过程中的误差来源，讨论如何减小误差。

6. 将实践作业表格贴在数学实践作业本上，供老师检查。

注意事项：
1. 测量时要小心谨慎，避免损坏物品。

2. 记录数据时要准确无误，保证计算结果的准确性。

3. 在计算过程中，要注意单位的统一（如：长度单位为米或厘米，面积单位为平方米或平方厘米，体积单位为立方米或立方厘米）。

4. 分析误差时，可以从测量工具、测量方法、计算过程等方面进行考虑。

通过这样的实践作业，学生可以在实际操作中加深对面积和体积计算的理解，提高数学应用能力，同时也可以培养细心、耐心和观察力等素质。

例题（2）:假设某地区人口数量N(t)随时间t 连续增长，即dN(t)/dt=λN(t),其中λ是人口增长率.易得其解 N(t)=N o e λt ,N O 是该地区的初始人口。

如果考虑到移民以速度V 进入该地区，则dN(t ）/dt=λN(t)+v微分方程的解为N(t)=N o e λt +v （e λt -1）/λ问题提出：假设该地区的初始人口有100万。

第一年内有43.5万移民迁入，第一年末总计人口156.4万，则43.5156.4100(1)λλλ=+-e e求该地区的人口增长率λ（一元方程求根）。

编程练习题1：对带有迁移的人口模型，试用几种非线性方程求根方法，确定模型公式中的人口增长率λ。

其满足：43.5156.4100(1)λλλ=+-e e设人口数量随着时间以固定的相对增长率变化。

领N(t)为t 食客的人口数量。

λ 为人口出生率。

1）人口数量的微分方程模型：dN(t)/dt=λN(t)2)指数模型: N(t)=N oe λt N O :初始时刻人口数量。

如果允许移民移入且移入速率v 为固定常数dN(t ）/dt=λN(t)+v3)有移民移入的指数模型：N(t)=N o e λt +v （e λt -1）/λ假设：N o =1000000 (人） ，v=435000（人/年） ，N(t)=1564000（人） 通过求解方程：43.5156.4100(1)λλλ=+-e e 的该地区人口的出生率λ=0.1。

设方程f(λ)=0在区间[0,1]内有根，二分法就是逐步收缩有根区间，最后得出所求的根。

具体过程如下区有根区间[0,1]得重点，将它分为两半，分点λo =0+1/2=0.5 这样就可以缩少有根区间。

有三种情可以出现：1）若f(λ)f(0)﹤0,则f(λ)在区间[0,0.5）内有零点;2）若f(λ)f(1)﹤0,则f(λ)在区间(0.5,1]内有零点;3）若f(λo)=0,则λo 再区间[0,1]内的零点。

小学生数学实验100例实验一：糖果计数Obj：培养小学生的计数能力Materials：糖果Procedure：1. 给每个小学生发放相同数量的糖果。

2. 让小学生一边将手中的糖果一个一个取出，一边用口数数。

3. 让他们将自己数的结果告诉老师，老师确认无误后，鼓励他们继续进行下一轮的计数。

4. 重复以上步骤，直到小学生们计数无误。

实验二：数字拼图Obj：提高小学生的数字认知和逻辑思维能力Materials：数字卡片、拼图板Procedure：1. 将数字卡片打乱顺序放在桌上。

2. 让小学生们按照数字的顺序将卡片拼在拼图板上。

3. 鼓励小学生们在完成之后互相检查答案，找出错误并及时修改。

实验三：趣味运算Obj：强化小学生的运算能力Materials：纸、铅笔Procedure：1. 给每个小学生发放纸和铅笔。

2. 出题者可以随机给出一道加法、减法或乘法的算式。

3. 小学生们写下自己的答案，并在完成后把纸张交给出题者。

4. 出题者检查答案，将答对的小学生召集起来并鼓励他们。

实验四：图形分类Obj：提高小学生的图形识别和分类能力Materials：各种图形卡片（正方形、长方形、圆形、三角形等）Procedure：1. 将各种图形卡片打乱顺序放在桌上。

2. 让小学生们按照图形的特征将卡片分类。

3. 鼓励小学生们在完成之后互相检查分类结果，并讨论不同分类方式的合理性和差异。

实验五：分数比较Obj：加深小学生对分数大小关系的理解Materials：纸、铅笔Procedure：1. 准备一些简单的分数题目，例如1/2、1/4、1/8等。

2. 让小学生们通过比较分子和分母的大小，判断分数的大小关系。

3. 引导小学生们用纸和铅笔练习绘制简单的分数图形，加深对分数大小关系的理解。

实验六：时钟读表Obj：提高小学生的时间概念和读表能力Materials：模拟时钟、题目卡片Procedure：1. 准备一些时钟读表题目卡片，包括小时和分钟的各种组合。

实验七T7:取不同的初值计算下列平方和形式的非线性规划，尽可能求出所有局部极小点，进而找出全局极小点，并对不同算法（搜索方向、搜索步长、数值梯度与分析梯度等）的结果进行分析、比较。

2)min 22222121212(1211)(4949812324681)x x x x x x +-++++-4)min 100θ2221/222312123{[χ-10(χ,χ)]+[(χ+χ)-1]}+χ 其中1(), >0 2(,)11(), <0 22arctg arctg πθπ21112211⎧χχχ⎪⎪χχ=⎨⎪χχ+χ⎪⎩ 解：2）在matlab 中输入程序（exam0705grad.m ，exam0705grad_run.m ）： function [f,g]=exam0705grad(x)f=(x(1)^2+12*x(2)-11)^2+(49*x(1)^2+49*x(2)^2+81*x(1)+2324*x(2)-681)^2;% compute the function value at xif nargout > 1 % fun called with 2 output argumentsg(1)=2*(98*x(1) + 81)*(49*x(1)^2 + 81*x(1) + 49*x(2)^2 + 2324*x(2) - 681) + 4*x(1)*(x(1)^2 + 12*x(2) - 11); % compute the gradient evaluated at xg(2)=288*x(2) + 2*(98*x(2) + 2324)*(49*x(1)^2 + 81*x(1) + 49*x(2)^2 + 2324*x(2) - 681) + 24*x(1)^2 - 264;endclear all ;clc;% comparing different algorithms: using gradient vectorformat short ex0=[-1.9,2];'---case1: bfgs, hybrid 2,3 poly-------'opt1=optimset('LargeScale','off', 'MaxFunEvals',1000,'GradObj','on');[x1,v1,exit1,out1]=fminunc(@exam0705grad,x0,opt1)pause'---case2: dfp, hybrid 2,3 poly-------'fopt=optimset(opt1,'HessUpdate','dfp');[x2,v2,exit2,out2]=fminunc(@exam0705grad,x0,fopt) pause'---case3: bfgs, hybrid 2,3 poly-------'fopt=optimset(opt1,'HessUpdate','bfgs');[x3,v3,exit3,out3]=fminunc(@exam0705grad,x0,fopt) pause'---case4: steep, hybrid 2,3 poly-------'fopt=optimset(opt1,'HessUpdate','steepdesc');[x4,v4,exit4,out4]=fminunc(@exam0705grad,x0,fopt) pause'---case5: bfgs, 3rd poly-------'opt2=optimset(opt1,'LineSearchType','cubicpoly'); [x5,v5,exit5,out5]=fminunc(@exam0705grad,x0,opt2) pause'---case6: dfp, 3rd poly-------'fopt=optimset(opt2,'HessUpdate','dfp');[x6,v6,exit6,out6]=fminunc(@exam0705grad,x0,fopt) pause'---case7:bfgs , 3rd poly-------'fopt=optimset(opt2,'HessUpdate','bfgs');[x7,v7,exit7,out7]=fminunc(@exam0705grad,x0,fopt) pause'---case8: steep, 3rd poly-------'fopt=optimset(opt2,'HessUpdate','steepdesc');[x8,v8,exit8,out8]=fminunc(@exam0705grad,x0,fopt)pause'++++ results of solutions ++++++'solutions=[x1;x2;x3;x4;x5;x6;x7;x8];funvalues=[v1;v2;v3;v4;v5;v6;v7;v8];iterations=[out1.funcCount;out2.funcCount;out3.funcCount;out4.funcCou nt;out5.funcCount;out6.funcCount;out7.funcCount;out8.funcCount]; [solutions,funvalues,iterations]则输出：x1 =-2.8997e+000 2.1583e-001v1 =3.2329e-006exit1 =1out1 =iterations: 32funcCount: 41stepsize: 1firstorderopt: 2.3873e+000algorithm: 'medium-scale: Quasi-Newton line search' message: [1x438 char]x2 =-2.3709e+000 2.5629e-001v2 =6.8300e+000exit2 =out2 =iterations: 401funcCount: 422stepsize: 1firstorderopt: 5.7455e+003algorithm: 'medium-scale: Quasi-Newton line search' message: [1x128 char]x3 =-2.8997e+000 2.1583e-001v3 =3.2329e-006exit3 =1out3 =iterations: 32funcCount: 41stepsize: 1firstorderopt: 2.3873e+000algorithm: 'medium-scale: Quasi-Newton line search' message: [1x438 char]x4 =-2.0594e+000 2.7379e-001v4 =1.2063e+001exit4 =out4 =iterations: 118funcCount: 1000stepsize: 4.7397e-006firstorderopt: 1.7291e+002algorithm: 'medium-scale: Quasi-Newton line search' message: [1x144 char]x5 =-2.8997e+000 2.1583e-001v5 =3.2329e-006exit5 =1out5 =iterations: 32funcCount: 41stepsize: 1firstorderopt: 2.3873e+000algorithm: 'medium-scale: Quasi-Newton line search' message: [1x438 char]x6 =-2.3709e+000 2.5629e-001v6 =6.8300e+000exit6 =out6 =iterations: 401funcCount: 422stepsize: 1firstorderopt: 5.7455e+003algorithm: 'medium-scale: Quasi-Newton line search'message: [1x128 char]x7 =-2.8997e+000 2.1583e-001v7 =3.2329e-006exit7 =1out7 =iterations: 32funcCount: 41stepsize: 1firstorderopt: 2.3873e+000algorithm: 'medium-scale: Quasi-Newton line search' message: [1x438 char]x8 =-2.0594e+000 2.7379e-001v8 =1.2063e+001exit8 =out8 =iterations: 118funcCount: 1000stepsize: 4.7397e-006firstorderopt: 1.7291e+002algorithm: 'medium-scale: Quasi-Newton line search' message: [1x144 char]ans =++++ results of solutions ++++++ans =-2.8997e+000 2.1583e-001 3.2329e-006 4.1000e+001-2.3709e+000 2.5629e-001 6.8300e+000 4.2200e+002-2.8997e+000 2.1583e-001 3.2329e-006 4.1000e+001-2.0594e+000 2.7379e-001 1.2063e+001 1.0000e+003-2.8997e+000 2.1583e-001 3.2329e-006 4.1000e+001-2.3709e+000 2.5629e-001 6.8300e+000 4.2200e+002-2.8997e+000 2.1583e-001 3.2329e-006 4.1000e+001-2.0594e+000 2.7379e-001 1.2063e+001 1.0000e+003改变x0,程序见附序（di1tix0.m），因太过繁琐，只输出最后x的值，输出：ans =-2.8956e+000 2.1618e-001 4.6001e-004 4.9000e+001-2.9377e+000 2.1295e-001 1.0877e+000 4.6600e+002-2.8956e+000 2.1618e-001 4.6001e-004 4.9000e+001-1.4106e+000 2.9837e-001 2.9482e+001 1.0000e+003-2.8956e+000 2.1618e-001 4.6001e-004 4.9000e+001-2.9377e+000 2.1295e-001 1.0877e+000 4.6600e+002-2.8956e+000 2.1618e-001 4.6001e-004 4.9000e+001-1.4106e+000 2.9837e-001 2.9482e+001 1.0000e+0034）程序见（exam07052grad.m， Untitled.m），输出结果：-1.9000e+000 1.0000e+000 2.0000e+000 5.0213e+002 1.6000e+001-1.9000e+000 1.0000e+000 2.0000e+000 5.0213e+002 1.6000e+001-1.9000e+000 1.0000e+000 2.0000e+000 5.0213e+002 1.6000e+001-1.9000e+000 1.0000e+000 2.0000e+000 5.0213e+002 1.6000e+001-1.9000e+000 1.0000e+000 2.0000e+000 5.0213e+002 1.6000e+001-1.9000e+000 1.0000e+000 2.0000e+000 5.0213e+002 1.6000e+001-1.9000e+000 1.0000e+000 2.0000e+000 5.0213e+002 1.6000e+001-1.9000e+000 1.0000e+000 2.0000e+000 5.0213e+002 1.6000e+001改变初值x0后程序见Untitled1.m，输出结果：-1.9000e+000 2.0000e+000 2.0000e+000 2.9923e+002 1.7000e+001-1.9000e+000 2.0000e+000 2.0000e+000 2.9923e+002 1.7000e+001-1.9000e+000 2.0000e+000 2.0000e+000 2.9923e+002 1.7000e+001-1.9000e+000 2.0000e+000 2.0000e+000 2.9923e+002 1.7000e+001-1.9000e+000 2.0000e+000 2.0000e+000 2.9923e+002 1.7000e+001 -1.9000e+000 2.0000e+000 2.0000e+000 2.9923e+002 1.7000e+001 -1.9000e+000 2.0000e+000 2.0000e+000 2.9923e+002 1.7000e+001 -1.9000e+000 2.0000e+000 2.0000e+000 2.9923e+002 1.7000e+001 结论：从2）4）输出观察和比较数据可以看出改变x0,最优解随之改变，而bfgs 公式，混合2,3次插值，求得的局部最优解最接近全局最优解。