3 基本几何体的投影解析

几何体的投影在几何学中，投影是指由三维空间中的一个物体到一个二维平面上的映射。

几何体的投影可以帮助我们更好地理解其形状和特征，并在实际应用中起到重要的作用。

本文将介绍几何体的投影原理、常见几何体的投影特征以及投影在不同领域的应用。

一、投影原理几何体的投影是指将三维物体的每个点沿着一个特定的方向映射到一个平面上的点。

这个过程可以类比为日光通过云层投射在地面上形成的阴影。

在几何学中，常用的投影方法有平行投影和透视投影。

1. 平行投影平行投影是指将几何体的每个点沿着平行于投影平面的方向进行投影。

在平行投影中，我们可以得到一个保持距离和角度不变的二维投影。

例如，当我们将一个立方体进行平行投影时，其投影形状将仍然是一个正方形。

2. 透视投影透视投影是指将几何体的每个点沿着一个特定的方向进行投影，使得远离观察平面的点被投影到平面上的点集更远离观察点的呈现更小。

透视投影是模拟人眼在观察物体时产生的效果。

在透视投影中，远离观察平面的部分将更小，而靠近观察平面的部分将更大。

二、常见几何体的投影特征不同的几何体在投影过程中会呈现出不同的特征和形状。

下面将介绍一些常见几何体的投影特征。

1. 点的投影点是几何学中最简单的几何体，其投影将落在投影平面上的一个点。

由于点本身没有具体的形状和大小，其投影将保持与原点位置相同的特点。

2. 直线的投影直线在投影平面上的投影将是一条直线，与原直线平行。

这是由于投影过程中直线的每个点都会在投影平面上形成一个对应的投影点。

3. 平面的投影平面的投影将在投影平面上形成一个与原平面平行的平面。

由于平面本身没有体积，其投影将保持原平面的形状和大小。

4. 三角形的投影三角形投影的特点是在投影平面上形成一个与原三角形相似的三角形。

其形状和大小取决于观察角度和投影方向。

5. 立方体的投影立方体在平行投影中的投影形状将是一个正方形，其边长与原立方体的边长相等。

在透视投影中，立方体的投影将呈现出近大远小的效果，与实际观察到的立方体形状一致。

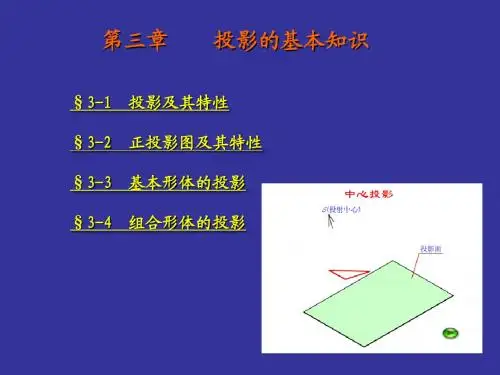
第三章投影的基本知识§3-1投影及其特性§3-2正投影图及其特性§3-3基本形体的投影§3-4组合形体的投影投影法的基本概念一、投影的基本概念二、投影法分类把空间形体表示在平面上，是以投影法为基础的。

投影法源出于日常生活中光的投射成影这个物理现象。

例如，当电灯光照射室内的一张桌子时，必有影子落在地板上；如果把桌于搬到太阳光下，那么，必有影子落在地面上。

§3-1投影及其特性假设要画出一个房屋形体的图形（图a），可在形体前面设置一个光源S （例如电灯），在光线的照射下，形体将在它背后的平面P 上投落一个灰黑的多边形的影。

这个影能反映出形体的轮廓，但表达不出形体各部分的形状。

假设光源发出的光线，能够透过形体而将各个顶点和各根侧棱都在平面P上投落它们的影，这些点和线的影将组成一个能够反映形体各部分形状的图形（图b），这个图形称为形体的投影。

光源S称为投射中心。

投影所在的平面P称为投影面。

连接投射中心与形体上各点的直线称为投射线。

通过一点的投射线与投影面P相交，所得交点就是该点在平面P上的投影。

作出形体投影的方法，称为投影法。

S投影中心投射线A空间点投影ba投影面P B空间点投影的基本概念投影三条件：①投影中心及投射线②投影面（不通过投影中心）③表达对象（空间几何元素或几何形体）投影——通过表达对象的一系列投射线与投影面的交点的总和。

投影法——获得投影的方法。

投影法的分类：投影中心投影平行投影斜投影正投影斜投影正投影投影面P中心投影中心投影法S 投射中心cba投射线A CB表达对象投影中心S 距投影面P 有限远中心投影法当投影中心S距投影面P为有限远时，所有的投射线都从投影中心一点出发（如同人眼观看物体或电灯照射物体），这种投影方法称为中心投影法。

用中心投影法获得的投影通常能反应表达对象的三维空间形态，立体感强，但度量性差。

这种图习惯上称之为透视图。

分析上图，我们可以得到中心投影的两条基本特性：1）直线的投影，在一般情况下仍为直线；2）点在直线上，则该点的投影必位在该直线的投影上。

数学知识点：空间几何体的三视图_知识点总结光由一点向外散射形成的投影叫做中心投影，其投影的大小随物体与投影中心间距离的变化而变化。

平行投影：在一束平行光线照射下形成的投影叫做平行投影。

在平行投影中，投影线正对着投影面时，叫做正投影，否则叫做斜投影。

空间几何体的三视图：光线从几何体的前面向后面正投影，得到投影图，叫做几何体的正视图；光线从几何体的左面向右面正投影，得到投影图，叫做几何体的侧视图；从几何体的上面向下面正投影，得到投影图,高考地理，叫做几何体的俯视图。

几何体的正视图、侧视图、俯视图统称为几何体的三视图。

注：正视图反映了物体上下、左右的位置关系，即反映了物体的高度和长度；俯视图反映了物体左右、前后的位置关系，即反映了物体的长度和宽度；侧视图反映了物体上下、前后的位置关系，即反映了物体的高度和宽度。

平行投影与中心投影的区别和联系:①平行投影的投射线都互相平行，中心投影的投射线是由同一个点发出的．如图所示，②平行投影是对物体投影后得到与物体等大小、等形状的投影；中心投影是对物体投影后得到比原物体大的、形状与原物体的正投影相似的投影．③中心投影和平行投影都是空间图形的基本画法，平行投影包括斜二测画法和三视图．中心投影后的图形与原图形相比虽然改变较多，但直观性强，看起来与人的视觉效果一致，最像原来的物体．④画实际效果图时，一般用中心投影法，画立体几何中的图形时一般用平行投影法．画三视图的规则:①画三视图的规则是正侧一样高，正俯一样长，俯侧一样宽．即正视图、侧视图一样高，正视图、俯视图一样长，俯视图、侧视图一样宽;②画三视图时应注意：被挡住的轮廓线画成虚线，能看见的轮廓线和棱用实线表示，不能看见的轮廓线和棱用虚线表示，尺寸线用细实线标出；D表示直径，R表示半径；单位不注明时按mm计;③对于简单的几何体，如一块砖，向两个互相垂直的平面作正投影，就能真实地反映它的大小和形状．一般只画出它的正视图和俯视图（二视图）．对于复杂的几何体，三视图可能还不足以反映它的大小和形状，还需要更多的投射平面．。

第三章　基本几何体的投影通常所说的基本几何体，包括棱柱体、棱锥体、圆柱体、圆锥体、球体和环等。

前两种立体的表面都是平面，称为平面立体；其余四种的表面是回转面或回转面与平面，称为回转体。

本章主要研究这些基本几何体的投影特性及其作图方法。

§3－1　平面立体的投影一、棱柱体的投影图３－１是五棱柱体和它的投影图。

该五棱柱体的顶面和底面均处于水平位置，其水平投影反映实形，正面和侧面投影均积聚成水平直线。

棱柱的五个侧棱面中最后的棱面DEE１D１处于正平面的位置，其正面投影反映实形，是不可见的面，故DD１、EE１两条棱线的正面投影d′d′１、e′e′１画成虚线，该棱面的水平投影和侧面投影积聚成直线。

其余四个侧棱面均为铅垂面，它们的水平投影都积聚成直线，正面投影和侧面投影为比实形小的矩形（类似形）。

图３－１　五棱柱体的投影画图时，一般先画反映底面实形的那个投影（即水平投影），然后再画正面和侧面投影，如图３－１ｂ所示。

在实际生产中所用的图纸都不必画出投影轴，如图３－１ｃ所示，但三个投影必须保持左右、上下、前后的对应关系，即V 、H 两面投影左右对正，V 、W 两面投影上下平齐，H 、W 两面投影前后相等。

二、棱锥体的投影图３－２是正三棱锥体和它的投影图。

该三棱锥体的底面处于水平位置，其水平面投影反映实形，正面和侧面投影积聚成水平直线。

三棱锥的右侧棱面SBC 为正垂面，其正面投影s ′b ′c ′积聚成直线，水平面投影sbc 和侧面投影s ″b ″c ″为类似形。

前棱面SAB 和后棱面SAC 均为一般位置平面，因而，它们的三面投影均为类似形（正面投影两个三角形重合）。

图３－２　正三棱锥体的投影画图时，先画出底面三角形ABC 和锥顶S 的投影，然后顺次连接各棱线SA 、SB 、SC 的同面投影，如图３－２ｂ所示。

通过棱柱和棱锥体的投影分析，可归纳如下几点：１）由于平面立体的棱线是直线，所以画平面立体的投影图就是先画出各棱线交点的投影，然后顺次连线，并注意区分可见性。

立体几何体的投影投影是立体几何学中的一个重要概念，它可以帮助我们将三维的物体映射到二维空间中，从而更好地理解和分析这些物体。

本文将介绍立体几何体的投影原理、常见的投影方法，并结合实例详细说明。

一、投影原理在立体几何学中，投影是指将一个物体上的点映射到一个平面上的过程。

我们通常使用视点和投影平面来进行投影操作。

视点是观察者的位置，而投影平面是观察者所处的平面。

根据视点和投影平面的位置不同，投影可以分为正射投影和透视投影两种常见方式。

1. 正射投影正射投影是指当视点距离物体足够远时，物体的投影基本上保持原有的形状和大小，只是发生了平移。

在正射投影中，投影平面与视平面平行，通过物体上的每个点与投影平面的垂直线，将点投影到投影平面上。

2. 透视投影透视投影是指当视点较近物体时，物体的投影会发生透视变形。

在透视投影中，投影平面与视平面不平行。

根据视点与投影平面的距离不同，透视投影可以分为近大远小和近小远大两种情况。

近大远小是指当视点离物体较近时，物体在投影平面上的投影会比实际物体大。

近小远大则是指当视点离物体较远时，物体在投影平面上的投影会比实际物体小。

二、常见的投影方法1. 正交投影正交投影是指通过将物体上的每个点与投影平面的垂线相交的方式进行投影。

在正交投影中，平行于投影平面的线段在投影过程中会保持平行，不会出现透视变形。

正交投影常用于工程制图和设计中。

2. 透视投影透视投影是指通过从视点到物体上每个点的视线来进行投影。

透视投影可以更真实地模拟人眼观察物体时的效果，使得投影具有透视变形的特点。

透视投影常用于艺术绘画和建筑设计中。

三、实例说明以一个立方体为例，来说明不同投影方式的应用。

1. 正射投影当投影平面与立方体的一条边平行时，可得到立方体在投影平面上的正射投影。

在这种投影中，所有的线段保持平行，且长度相等，不会发生透视变形。

2. 透视投影当投影平面不与立方体的任何一条边平行时，可得到立方体在投影平面上的透视投影。