基本几何体的投影
- 格式:ppt
- 大小:3.98 MB
- 文档页数:46



空间几何体的投影计算投影是几何学中的一个重要概念,它可以帮助我们理解和分析三维空间中的几何体。
本文将讨论如何计算空间几何体的投影,并介绍常见几何体的投影计算方法。
1. 直线的投影计算在三维空间中,一条直线可以用参数方程表示为:x = x0 + t * ay = y0 + t * bz = z0 + t * c其中(x0, y0, z0)为直线上的一点,(a, b, c)为直线的方向向量,t为参数。
直线在平面上的投影可以通过将直线的参数方程代入平面的方程来计算。
设平面方程为Ax + By + Cz + D = 0,则直线在平面上的投影为:x = x0 + t * a - (a * Ax0 + b * Ay0 + c * Az0 + D) * a / (a^2 + b^2 + c^2)y = y0 + t * b - (a * Ax0 + b * Ay0 + c * Az0 + D) * b / (a^2 + b^2 +c^2)z = z0 + t * c - (a * Ax0 + b * Ay0 + c * Az0 + D) * c / (a^2 + b^2 + c^2)2. 球体的投影计算球体在三维空间中的投影是一个圆。
以球心为原点建立球坐标系,球心到球上任意一点的向量可以表示为:x = r * sinθ * cosφy = r * sinθ * sinφz = r * cosθ其中r为球的半径,θ为极角,φ为方位角。
球体在平面上的投影也是一个圆,其圆心和半径可以通过球坐标系中的坐标转换得到。
设平面方程为Ax + By + Cz + D = 0,球的投影圆的半径为R,则圆心在球坐标系中的极角和方位角可以通过以下公式计算:cosθ = -D / √(A^2 + B^2 + C^2)sinθ * cosφ = -A / √(A^2 + B^2 + C^2)sinθ * sinφ = -B / √(A^2 + B^2 + C^2)圆心在球坐标系中的三维坐标为:x = R * sin(π/2 - θ) * cos(π - φ)y = R * sin(π/2 - θ) * sin(π - φ)z = R * cos(π/2 - θ)3. 长方体的投影计算长方体在三维空间中的投影是一个矩形。






第六节几何体的投影机器上的零件,不论形状多么复杂,都可以看作是由基本几何体按照不同的方式组合而成的。
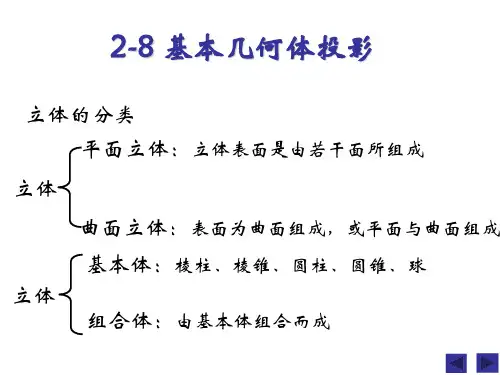
1、基本几何体——表面规则而单一的几何体。
按其表面性质,可以分为平面立体和曲面立体两类。
2、平面立体——立体表面全部由平面所围成的立体,如棱柱和棱锥等。
2、曲面立体——立体表面全部由曲面或曲面和平面所围成的立体,如圆柱、圆锥、圆球等。
曲面立体也称为回转体。
一、平面立体的投影及表面取点1、棱柱棱柱由两个底面和棱面组成,棱面与棱面的交线称为棱线,棱线互相平行。
棱线与底面垂直的棱柱称为正棱柱。
本节仅讨论正棱柱的投影。
(1)棱柱的投影以正六棱柱为例。
如图(a)所示为一正六棱柱,由上、下两个底面(正六边形)和六个棱面(长方形)组成。
设将其放置成上、下底面与水平投影面平行,并有两个棱面平行于正投影面面。
上、下两底面均为水平面,它们的水平投影重合并反映实形,正面及侧面投影积聚为两条相互平行的直线。
六个棱面中的前、后两个为正平面,它们的正面投影反映实形,水平投影及侧面投影积聚为一直线。
其他四个棱面均为铅垂面,其水平投影均积聚为直线,正面投影和侧面投影均为类似形。
(a)立体图(b)投影图正六棱柱的投影及表面上的点总结正棱柱的投影特征:当棱柱的底面平行某一个投影面时,则棱柱在该投影面上投影的外轮廓为与其底面全等的正多边形,而另外两个投影则由若干个相邻的矩形线框所组成。
(2)棱柱表面上点的投影方法:利用点所在的面的积聚性法。
(因为正棱柱的各个面均为特殊位置面,均具有积聚性。
)平面立体表面上取点实际就是在平面上取点。
首先应确定点位于立体的哪个平面上,并分析该平面的投影特性,然后再根据点的投影规律求得。
举例:如图(b)所示,已知棱柱表面上点M的正面投影m′,求作它的其他两面投影m、m″。
因为m′可见,所以点M必在面ABCD上。
此棱面是铅垂面,其水平投影积聚成一条直为可见,故m″也为可见。
特别强调:点与积聚成直线的平面重影时,不加括号。