完整word版有限元分析轴对称问题

有限元分析大作业报告试题1：一、问题描述及数学建模图示无限长刚性地基上的三角形大坝，受齐顶的水压力作用，试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析，并对以下几种计算方案进行比较：（1）分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算；（2）分别采用不同数量的三节点常应变单元计算；（3）当选常应变三角单元时，分别采用不同划分方案计算。

该问题属于平面应变问题，大坝所受的载荷为面载荷，分布情况及方向如图所示。

二、采用相同单元数目的三节点常应变单元和六节点三角形单元计算1、有限元建模（1）设置计算类型：两者因几何条件和载荷条件均满足平面应变问题，故均取Preferences 为Structural（2）选择单元类型：三节点常应变单元选择的类型是Solid Quad 4 node182；六节点三角形单元选择的类型是Solid Quad 8 node183。

因研究的问题为平面应变问题，故对Element behavior（K3）设置为plane strain。

（3）定义材料参数：弹性模量E=2.1e11，泊松比σ=0.3（4）建几何模型：生成特征点；生成坝体截面（5）网格化分：划分网格时，拾取lineAB和lineBC，设定input NDIV 为15；拾取lineAC，设定input NDIV 为20，选择网格划分方式为Tri+Mapped，最后得到600个单元。

（6)模型施加约束：约束采用的是对底面BC 全约束。

大坝所受载荷形式为Pressure ，作用在AB 面上，分析时施加在L AB 上，方向水平向右，载荷大小沿L AB 由小到大均匀分布。

以B 为坐标原点，BA 方向为纵轴y ，则沿着y 方向的受力大小可表示为：}{*980098000)10(Y y g gh P -=-==ρρ2、 计算结果及结果分析 （1） 三节点常应变单元三节点常应变单元的位移分布图三节点常应变单元的应力分布图（2）六节点三角形单元六节点三角形单元的变形分布图六节点三角形单元的应力分布图①最大位移都发生在A点，即大坝顶端，最大应力发生在B点附近，即坝底和水的交界处，且整体应力和位移变化分布趋势相似，符合实际情况；②结果显示三节点和六节点单元分析出来的最大应力值相差较大，原因可能是B点产生了虚假应力，造成了最大应力值的不准确性。

肯定有bug。

仅供参考。

1401052200隐式方法与显式方法：==静态隐式方法：不适用于短时高速下的大变形。

基于虚功原理，一般需要迭代（除迭代法外还有直接法）。

可能遇到迭代过程不收敛，以及方程组病态无确定解的问题。

ANSYS默认使用的方法。

动态显式方法：可用于短时、高速下的大变形。

基于动力学方程，每步计算形成新的刚度矩阵，无需迭代，不存在收敛性问题。

LS-DYDA模块（ANSYS中也包含）默认使用。

如何判断有限元的分析结果是正确的？1.有限元分析的结果能否与模型简化后存在的解析解对应；2.有限点处的计算结果与实验结果吻合；3.结果收敛；4.与实际经验吻合；……【结合书上P168】力学应力、温度热学分析提倡使用对称性，但不是所有的情况都能使用对称性，比如结构件的振动。

有限元方法：求解偏微分方程，基础为加权残值法。

求解有限元方程本质为解线性方程组。

ADD：要求所ADD的为同一种材料。

低阶单元：只有角节点，没有边中点或面内点的单元。

（目前已不使用面内点）高阶单元：不但有角节点，还有边中点或面内点的单元。

静态小变形使用高阶单元。

动态大变形使用低阶单元。

连续介质单元：求解得到位移。

结构单元：求解得到位移和转角。

求解结果的位移精度大于应力精度。

网格类型：三角形，四边形；四面体（三棱锥），五面体（三棱柱），六面体。

根据自由度关系，单元节点间存在铰接（自由度不同）和刚接（自由度相同）的关系。

连续介质单元也有一维单元（如接触关系）。

工字钢既可以使用梁单元，也可以使用连续介质单元。

对于直接法的求解效率：带宽解法：ANSYS的默认求解法；尽量减小单元内节点号差值从而减小带宽。

波阵解法：ABAQUS的默认求解法；尽量减小绕一节点所连接的单元号的差值从而减小波阵宽。

节点编号，从角节点开始，逆时针。

==使用子结构，可减少对内存的占用，但会增加时间消耗。

连续介质单元剖分后，只在节点上存在关系，公共边上位移相同，不出现重叠或分离。

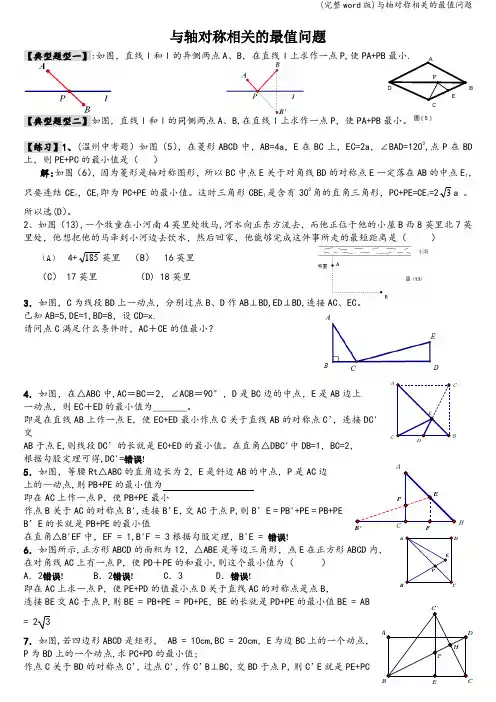
图（5）CEDPBA 与轴对称相关的最值问题【典型题型一】:如图，直线l 和l 的异侧两点A 、B ，在直线l 上求作一点P,使PA+PB 最小.【典型题型二】如图，直线l 和l 的同侧两点A 、B,在直线l 上求作一点P ，使PA+PB 最小。

【练习】1、(温州中考题）如图（5），在菱形ABCD 中，AB=4a ，E 在BC 上，EC=2a ，∠BAD=1200,点P 在BD 上，则PE+PC 的最小值是（ ）解:如图（6），因为菱形是轴对称图形，所以BC 中点E 关于对角线BD 的对称点E 一定落在AB 的中点E 1，只要连结CE 1，CE 1即为PC+PE 的最小值。

这时三角形CBE 1是含有300角的直角三角形，PC+PE=CE 1=23a 。

所以选(D ）。

2、如图（13),一个牧童在小河南4英里处牧马,河水向正东方流去，而他正位于他的小屋B 西8英里北7英里处，他想把他的马牵到小河边去饮水，然后回家，他能够完成这件事所走的最短距离是（ ）（A ） 4+185英里 （B ） 16英里（C ） 17英里 （D) 18英里3．如图，C 为线段BD 上一动点，分别过点B 、D 作AB ⊥BD,ED ⊥BD,连接AC 、EC 。

已知AB=5,DE=1,BD=8，设CD=x.请问点C 满足什么条件时，AC ＋CE 的值最小？4．如图，在△ABC 中,AC ＝BC ＝2，∠ACB ＝90°，D 是BC 边的中点，E 是AB 边上 一动点，则EC ＋ED 的最小值为_______。

即是在直线AB 上作一点E ，使EC+ED 最小作点C 关于直线AB 的对称点C ’，连接DC'交 AB 于点E,则线段DC ’的长就是EC+ED 的最小值。

在直角△DBC'中DB=1，BC=2， 根据勾股定理可得,DC'=错误!5．如图，等腰Rt △ABC 的直角边长为2，E 是斜边AB 的中点，P 是AC 边 上的一动点,则PB+PE 的最小值为 即在AC 上作一点P ，使PB+PE 最小 作点B 关于AC 的对称点B',连接B ’E ，交AC 于点P,则B’E = PB'+PE = PB+PE B ’E 的长就是PB+PE 的最小值 在直角△B'EF 中，EF = 1,B'F = 3根据勾股定理，B'E = 错误!6．如图所示,正方形ABCD 的面积为12，△ABE 是等边三角形，点E 在正方形ABCD 内， 在对角线AC 上有一点P ，使PD ＋PE 的和最小,则这个最小值为（ ） A ．2错误! B ．2错误! C ．3 D ．错误!即在AC 上求一点P ，使PE+PD 的值最小点D 关于直线AC 的对称点是点B ，连接BE 交AC 于点P,则BE = PB+PE = PD+PE ，BE 的长就是PD+PE 的最小值BE = AB = 2 37．如图,若四边形ABCD 是矩形， AB = 10cm,BC = 20cm ，E 为边BC 上的一个动点，P 为BD 上的一个动点,求PC+PD 的最小值; 作点C 关于BD 的对称点C ’，过点C'，作C ’B ⊥BC ，交BD 于点P ，则C ’E 就是PE+PCFP B'EＡＣＢＣ'DＡＣＢEPE BCD A H PEC'D ACB的最小值直角△BCD 中，CH = 错误!错误！未定义书签。

轴对称中几何动点最值问题总结轴对称的作用是“搬点移线”，可以把图形中比较分散、缺乏联系的元素集中到“新的图形”中，为应用某些基本定理提供方便。

比如我们可以利用轴对称性质求几何图形中一些线段和的最大值或最小值问题。

利用轴对称的性质解决几何图形中的最值问题借助的主要基本定理有三个：（1）两点之间线段最短；（2）三角形两边之和大于第三边；（3）垂线段最短。

初中阶段利用轴对称性质求最值的题目可以归结为：两点一线，两点两线，点两线三类线段和的最值问题。

下面对三类线段和的最值问题进行分析、讨论。

问题特征：已知两个定点位于一条直线的同一侧，在直线上求一动点的位置，使动点与定点线段和最短。

核心思路：这类最值问题所求的线段和中只有一个动点，解决这类题目的方法是找出任一定点关于直线的对称点，连结这个对称点与另一定点，交直线于一点，交点即为动点满足最值的位置。

方法：1.定点过动点所在直线做对称。

2. 连结对称点与另一个定点，则直线段长度就是我们所求。

变异类型：实际考题中，经常利用本身就具有对称性质的图形，比如等腰三角形，等边三角形、正方形、圆、二次函数、直角梯形等图形，即其中一个定点的对称点就在这个图形上。

1. 如图，直线I和I的同侧两点A B,在直线I上求作一点P，使PA+PB最小。

问题特征：已知一个定点位于平面内两相交直线之间，分别在两直线上确定两个动点使线段和最短核心思路：这类问题实际上是两点两线段最值问题的变式，通过做这一定点关于两条线的对称点，实现“搬点移线”，把线段“移”到同一直线上来解决。

变异类型：1.如图，点P是/ MON内的一点，分别在OM ON上作点A, B。

使△PAB的周长最小。

（3）两点两线的最值问题：（两个动点+两个定点）问题特征：两动点，其中一个随另一个动（一个主动，一个从动），并且两动点间的距离保持不变。

核心思路：用平移方法，可把两动点变成一个动点，转化为“两个定点和一个动点”类型来解。

3 轴对称问题弹性力学空间问题中的轴对称问题是指，物体的几何形状、约束情况及所受的外力都对称于空间的某一根轴，因此在物体中通过该轴的任何平面都是对称面，所有应力、应变和位移也对称于该轴，这类问题称为轴对称问题。

研究轴对称问题时通常采用圆柱坐标系（r，θ，z），以z轴为对称轴。

轴对称问题实例如图3.1所示的受均布内压作用的长圆筒，通过Z轴的一个纵截面就是对称面图3.1受均布内压作用的长圆筒3.1 三角形截面环单元三结点单元位移函数图4-2 三结点单元轴对称问题分析中所使用的三结点单元，在对称面上是三角形，在整个弹性体中是三棱圆环，各单元中圆环形铰相联接。

三角形截面环单元的结点位移在轴对称问题中，弹性体内任意一点上，不存在切向位移，只存在径向位移u 和轴向位移w ，两个位移分量表示为，⎭⎬⎫⎩⎨⎧=w u f }{[][]Tmm j j i iT mT jT iew u w u w u==δδδδ}{单元结点位移轴对称问题的三结点三角形单元位移函数取为，⎭⎬⎫++=++=z r z r u 654321w αααααα⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∆=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧m j i m jim j i m j i u u u c c c b b b a a a 21321ααα根据结点位移，可得：⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∆=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧m j i m jim j i m j i w w w c c c b b b a a a 21654ααα单元形函数jm m j i r z z r a -=mmj ji iz r z r z r 11121=∆mj i z z b -=jm i r r c -=（i ，j ，m ）)(21z c r b a N i i i i ++∆=单元内任一点的位移{}[]{}em jim m j j i i m jim j iN N N w u w u w u N N N N N N w u f δ=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡=⎭⎬⎫⎩⎨⎧=00003.2 应变矩阵（几何矩阵）根据几何方程及单元内位移的表达式，可得：⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧∂∂+∂∂∂∂∂∂=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧r w z u z w ru r u zr z r γεεεθ应变矩阵)(21m m j j i i u b u b u b r u ++∆=∂∂)(21m m j j i i u f u f u f r u ++∆=rcz b r a f i i i ++=（下标轮换）)(21m m j j i i w c w c w c z w ++∆=∂∂)(21m m j j i i u c u c u c z u ++∆=∂∂)(21m m j j i i w b w b w b r w ++∆=∂∂应变矩阵[]{}em ji m m mm m jj jj j ii ii i zr z r B B B b c c f b b c c f b b c c f b δγεεεθ=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∆=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧00000000021),,(00021][m j i b c c f b A B i i i iii ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=3.3 应力矩阵由轴对称问题的物理方程，得到弹性矩阵，⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---------+-=)1(22100011101110111)21)(1()1(][μμμμμμμμμμμμμμμμμE D应力矩阵11A =-μμ2)1(221A =--μμ3)21)(1(4)1(A E=-+-μμμ令：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+-=21111110010101)21)(1()1(][A A A A AA A E D μμμ则弹性矩阵为：]][[][B D S =][][m j iS S S S =),,()(2]][[][2211113m j i b A c A c f b A c A f b A c A f b A B D S i ii i i i ii i i i i i ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++∆==由弹性矩阵[D ]和几何矩阵[B ]可以得到应力矩阵[S ]，由应力矩阵可知，除剪应力为常量，其它三个正应力分量都是r 、z 的函数。