材料力学第二章-11 温度应力和装配应力
- 格式:docx
- 大小:12.57 MB
- 文档页数:6



材料力学应力应变部分材料力学(应力应变部分)→规定载荷作用下,强度要求,就是指构件应有足够的抵抗破坏的能力。
刚度要求,就是指构件应有足够的抵抗变形的能力。
→变形的基本假设:连续性假设,均匀性假设,各向同性假设。
→沿不同方向力学性能不同的材料,称为各向异性材料,如木材、胶合板和某些人工合成材料。
→ 分布力表面力集中力(火车轮对钢轨压力,滚珠轴承对轴的反作用力)体积力是连续分布于物体内各点的力,例如物体的自重和惯性力等。
→动载荷,静载荷→应力p应分解为正应力? ,切应力τ。
26→应力单位pa,1pa=1N/m;常用Mpa,1Mpa=10pa。
第二章拉伸、压缩与剪切2.2 轴向拉伸或压缩时横截面上的内力和应力→习惯上,把拉伸的轴力规定为正,压缩时的轴力规定为负。
→用横截面上的应力来度量杆件的受力程度。
→FN=?A ;?(x)=FN(x)/A(x)2.3 直杆轴向拉伸或压缩时斜截面上的内力和应力α轴向拉伸(压缩)时,在杆件的横截面上,正应力为最大值;在与杆件轴线成45°的斜截面上,切应力为最大值。
最大切应力在数值上等于最大正应力的二分之一。
此外,α=90°时,?α=τα=0 ,这表示在平行于杆件轴线的纵向截面上无任何应力。
(应力,p=F/A,45°斜截面上,力→ ,面积→ 。
) 2.7 安全因数许用应力和安全因数的数值,可以在有关部门的一些规范中查到。
目前一般机械制造中,在静载的情况下,对塑性材料可取ns=1.2~2.5。
脆性材料均匀性较差,且断裂突然发生,有更大的危险性,所以取nb=2~3.5,甚至取到3~9。
2.8 轴向拉伸或压缩时的变形→胡克定律,当应力不超过材料的比例极限时,应力与应变成正比。
?=Eε,弹性模量E的值随材料而不同。
2222=ε=E=AE ;?l=AE ?FFL即,对长度相同,受力相等的杆件,有EA越大则变形Δl越小,所以称EA为杆件的抗拉/压刚度。
→泊松比,当应力不超过比例极限时横向应变ε’与轴向应变ε之比的绝对值是一个常数,即�O�O=μ。





材料力学(应力应变部分)→规定载荷作用下,强度要求,就是指构件应有足够的抵抗破坏的能力。
刚度要求,就是指构件应有足够的抵抗变形的能力。
→变形的基本假设:连续性假设,均匀性假设,各向同性假设。
→沿不同方向力学性能不同的材料,称为各向异性材料,如木材、胶合板和某些人工合成材料。
→ 分布力 表面力集中力(火车轮对钢轨压力,滚珠轴承对轴的反作用力) 体积力是连续分布于物体内各点的力,例如物体的自重和惯性力等。
→动载荷,静载荷→应力p 应分解为正应力σ ,切应力τ 。
→应力单位pa ,1pa=1N/m 2;常用Mpa ,1Mpa=106pa 。
第二章 拉伸、压缩与剪切2.2 轴向拉伸或压缩时横截面上的内力和应力→习惯上,把拉伸的轴力规定为正,压缩时的轴力规定为负。
→用横截面上的应力来度量杆件的受力程度。
→F N =σA ;σ(x)=F N (x)/A(x)2.3 直杆轴向拉伸或压缩时斜截面上的内力和应力 α轴向拉伸(压缩)时,在杆件的横截面上,正应力为最大值;在与杆件轴线成45°的斜截面上,切应力为最大值。
最大切应力在数值上等于最大正应力的二分之一。
此外,α=90°时,σα=τα=0 ,这表示在平行于杆件轴线的纵向截面上无任何应力。
(应力,p=F/A ,45°斜截面上,力→√22,面积→√22。
) 2.7 安全因数许用应力和安全因数的数值,可以在有关部门的一些规范中查到。
目前一般机械制造中,在静载的情况下,对塑性材料可取n s =1.2~2.5。
脆性材料均匀性较差,且断裂突然发生,有更大的危险性,所以取n b =2~3.5,甚至取到3~9。
2.8 轴向拉伸或压缩时的变形→胡克定律,当应力不超过材料的比例极限时,应力与应变成正比。
σ=Eε ,弹性模量E 的值随材料而不同。
∆l l=ε=σE =F AE ;∆l =FLAE即,对长度相同,受力相等的杆件,有EA 越大则变形Δl越小,所以称EA 为杆件的抗拉/压刚度。
《材料力学》课程授课教案课程编号:B03086课程中文名称:材料力学/ Material Mechanics课程总学时/学分: 76/4 (其中理论 60 学时,实验 16 学时)适用专业:过程控制专业、材料成型专业一、课程地位本课程是机械及土木类专业的主要技术基础课,其目的是掌握最基本的杆、杆系、刚架结构的计算原理和方法,了解各类结构的内力分布特征,为机械和土木类工程后续课程如结构力学、弹性力学、机械制造及设计类课程、混凝土结构设计、钢结构等打好力学基础,并培养结构分析与计算方面的能力,该课程须先修完高等数学、工程数学、大学物理、理论力学课程后学习。
二、教材及主要参考资料教材:刘鸿文主编《.材料力学》(I、 II).第四版高等教育出版社 2004年1月主要参考资料:1. 孙训方等编《.材料力学》(I、 II).第四版高等教育出版社2、胡增强编《材料力学学习指导》高等教育出版社3、顾志荣、吴永生编《材料力学学习方法及解题指导》同济大学出版社4、苟文选主编《材料力学导学、导教、导考(上、下册) 》西北工业大学出版社四、课时分配五、考核方式与成绩核定办法1. 考核方式:期末笔试+平时考核2. 成绩核定办法:笔试占70%,平时占30%六、授课方案第一章绪论1. 教学要求了解材料力学的任务,了解杆件变形基本形式。
掌握可变形固体的性质及其基本假设,熟练掌握应力、应变概念,2. 教学重点与难点重点:变形固体的性质及其基本假设、切应变。
难点:切应变概念。
3. 教学策略多媒体加板书讲授、课堂提问、练习,注意受力分析多采用板书讲授为好4. 参考书目:1、胡增强编《材料力学学习指导》高等教育出版社2、顾志荣、吴永生编《材料力学学习方法及解题指导》同济大学出版社3、苟文选主编《材料力学导学、导教、导考(上、下册) 》西北工业大学出版社5. 教学内容:1.1材料力学的任务为保证工程结构或机械的正常工作,构件应有足够的能力负担起应当承受的载荷。
材料力学---2绪论一、是非题1.1 材料力学主要研究杆件受力后变形与破坏的规律。
()1.2 内力只能是力。
()1.3 若物体各点均无位移,则该物体必定无变形。
()1.4 截面法是分析应力的基本方法。
()二、选择题1.5 构件的强度是指(),刚度是指(),稳定性是指()。
A. 在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持其原有的平衡状态的能力C. 在外力作用下构件抵抗破坏的能力1.6 根据均匀性假设,可认为构件的()在各点处相同。
A. 应力B. 应变C. 材料的弹性常数D. 位移1.7 下列结论中正确的是()A. 内力是应力的代数和B. 应力是内力的平均值C. 应力是内力的集度D. 内力必大于应力参考答案:1.1 √ 1.2 × 1.3 √ 1.4 × 1.5 C,A,B 1.6 C 1.7 C轴向拉压一、选择题1.衡。
设杆CD 截面面积为(A) q gA ρ=(B) (C) (D) 2. (A) (C) 3. 在A 和B 和点B (A) 0o ; (C) 45o ; 4. 为A (A)[]2A σ; (C) []A σ;5. (A) (C)6. 三杆结构如图所示。
今欲使杆一种措施?(A) 加大杆3的横截面面积; (B) 减小杆3的横截面面积; (C) (D) 增大α角。
7. 图示超静定结构中,梁AB 示杆1的伸长和杆2(A) 12sin 2sin l l αβ∆=∆; (B) 12cos 2cos l l αβ∆=∆; (C) 12sin 2sin l l βα∆=∆; (D) 12cos 2cos l l βα∆=∆。
8. 图示结构,AC 为刚性杆,杆(A) 两杆轴力均减小; (B) 两杆轴力均增大;(C) 杆1轴力减小,杆2(D) 杆1轴力增大,杆29. 结构由于温度变化,则:(A) (B) (C) (D) 静定结构中将引起应力和变形,超静定结构中将引起应力。
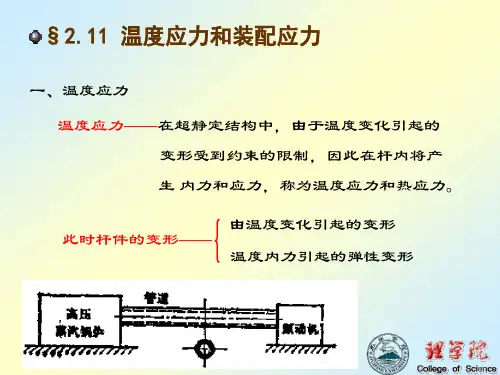
2-11 温度应力和装配应力
一、温度应力
超静定问题用三关系法求解
1、静力学关系
①取AB为研究对象
②变形受压
③列平衡方程
2、物理关系
①轴力引起的变形量
②温度引起的变形量
【分析】温度变化要涨开,轴力变化不允许涨
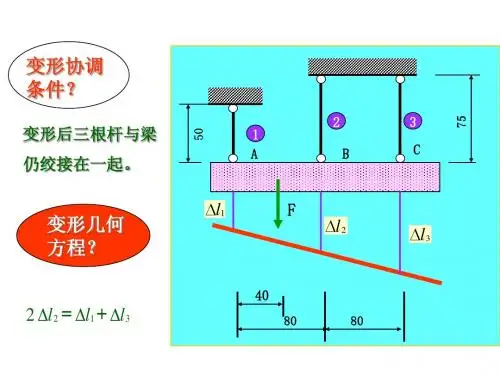
3、协调方程
6、求应力
代入应力=F/A
6、如何防止温度应力
〔一〕、温度不变AC拉伸取正BC压缩取负δ=AC-BC=0.1〔二〕、温度升高30℃
3.δ=△l
衡量受到3个力,3个点构成平面平行力系、两个方程、3个未知数、1次超静定问题
1、静力学关系
①确定研究对象〔安装后的AB横梁〕
N1+N3-N3=0
N1=N3
2、物理关系
△l1=△l3=?
△l2=?
3、协调关系
4、N1l/EA=△-N2l/EA
【练习】
1、静力学问题外载的一半使外面两杆变形量没有超过中间短柱长度1.5mm
2、超静定问题
变形量中的δ不用考虑
1、静力学关系
①-2aN1+3aN2-4aN3=0
2、物理关系
△l1 △l2 △l3
3、协调关系。
材料力学大连理工大学王博装配应力与温度应力典型静不定结构问题1———装配应力 静不定结构 ——?静定结构 ——无装配应力 ! AC BD B C A B C A已知 三杆EA 相同,1杆制造 误差δ, 求 装配内力 解题思路 因制造误差,装配时各杆必须变形,因此产生装配内力判断 一次静不定平衡方程 内力不可任意假设物理方程 胡克定律典型静不定结构问题1———装配应力 例题1几何方程: 12/cos l l αδ∆+∆= A C12 B αα 3D δ l A'⊿l 1 ⊿l 2A F N1 F N2 F N3 1杆伸长,应为拉力;2,3杆缩短 , 应为压力 装配应力是不容忽视的如 δ / l = 0.001 , E = 200GPa , α = 30°σ1 = 113 MPa , σ2 = σ3 = -65.2 MPaA C12 B αα 3D δl A'⊿l 1 ⊿l 2 A F N1 F N2 F N3不好典型静不定结构问题2———温度应力 静不定结构有温度内力 静定结构 无温度内力 A C BT C A C B D T C温度影响之物理方程 t l l tα∆=∆⊿l 1⊿l 2例题 2l a a AB O 1 2 例题: OAB 杆视为刚性,1,2两杆相同, 已知: EA , l , a , ∆ t , 求:温度变化引起1,2杆的内力。
解:1.判断:一次静不定。
2.几何方程:⊿l 2 = 2 ⊿l 13.平衡方程:∑M O =0 , F N1 a + F N2 2a = 0 F N1 = - 2 F N2αA 'B 'l A B O 1 2 a a F N1 F N24.物理方程:5.以上方程联解,得:EA l F t l l 1N 1+∆=∆α ⊿l 2 = 2⊿l 1 EAl F t l l 2N 2+∆=∆α⊿l 1⊿l 2l a a AB O 12 A 'B 't EA F ∆=α512N (拉)t EA F ∆-=α521N (压)t l l t α∆=∆N F F l l EA ∆=求解: 结构的温度应力? 思路: 温度变化引起杆的长度变化 多余约束限制了这个变化 引起温度内力 几何方程: 物理方程: 物理方程代入几何方程: 温度应力为: lAB 例题3t l l t α∆=∆0t F l l l ∆=∆+∆=N F F l l EA ∆=0N F l l l t EA α∆=∆+=N F E t Aσα==-∆总结与思考仅用静力平衡方程不能全部求解 1. 静不定问题 原因:未知量数目多于独立平衡方程数目 2. 解法关键: 建立几何方程 建立物理方程 从而可得补充方程3. 特点: 内力按刚度比分配4. 两个典型静不定问题:装配应力、温度应力5. 注意事项:正确判断静不定次数 变形假设与受力假设协调6. 静不定次数反应结构的冗余度,越大越可靠 AF C1 2 B αα 3D。
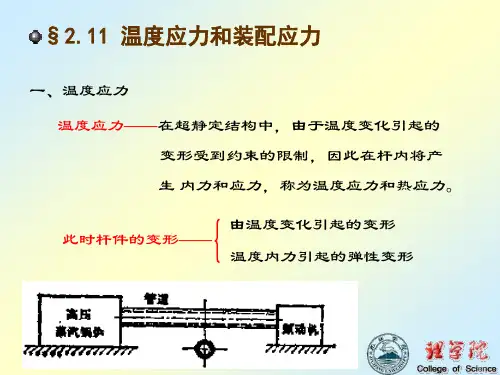
2-11 温度应力和装配应力
一、温度应力
超静定问题用三关系法求解
1、静力学关系
①取AB为研究对象
②变形受压
③列平衡方程
2、物理关系
①轴力引起的变形量
②温度引起的变形量
【分析】温度变化要涨开,轴力变化不允许涨
3、协调方程
6、求应力
代入应力=F/A
6、如何避免温度应力
(一)、温度不变AC拉伸取正BC压缩取负δ=AC-BC=0.1(二)、温度升高30℃
3.δ=△l
衡量受到3个力,3个点构成平面平行力系、两个方程、3
个未知数、1次超静定问题
1、静力学关系
①确定研究对象(安装后的AB横梁)
N1+N3-N3=0
N1=N3
2、物理关系
△l1=△l3=?
△l2=?
3、协调关系
4、N1l/EA=△-N2l/EA
【练习】
1、静力学问题外载的一半使外面两杆变形量没有超过中间短柱长度1.5mm
2、超静定问题
变形量中的δ不用考虑
1、静力学关系
①-2aN1+3aN2-4aN3=0
2、物理关系
△l1 △l2 △l3
3、协调关系。