三角函数的公式+五点作图+奇偶性+周期性

高中三角函数公式汇总与解析【引言】三角函数是高中数学中的一大重点内容，掌握三角函数的公式是学好数学的基础。

本文将对高中三角函数的公式进行汇总与解析，以帮助读者更好地理解和运用这些公式。

【正文】一、角度与弧度的转换在三角函数中，角可以用度数表示，也可以用弧度表示。

两者之间的转换关系如下：1度=π/180弧度1弧度=180/π度二、基本三角函数公式1. 正弦函数（sin）①定义域：实数集R②值域：[-1,1]③周期性：T=2π④奇偶性：a. sin(-x) = -sin(x)b. sin(x+π) = -sin(x)2. 余弦函数（cos）①定义域：实数集R②值域：[-1,1]③周期性：T=2π④奇偶性：a. cos(-x) = cos(x)b. cos(x+π) = -cos(x)3. 正切函数（tan）①定义域：x≠(2k+1)π/2，其中k为整数②值域：实数集R③周期性：T=π④奇偶性：a. tan(-x) = -tan(x)b. tan(x+π) = tan(x)三、和差角公式1.正弦函数：sin(A±B) = sin(A)cos(B)±cos(A)sin(B) 2.余弦函数：cos(A±B) = cos(A)cos(B)∓sin(A)sin(B)tan(A±B) = (tan(A)±tan(B))/(1∓tan(A)tan(B))四、倍角公式1.正弦函数：sin(2A) = 2sin(A)cos(A)2.余弦函数：cos(2A) = cos²(A) - sin²(A) = 2cos²(A) - 1 = 1 - 2sin²(A) 3.正切函数：tan(2A) = (2tan(A))/(1 - tan²(A))五、半角公式1.正弦函数：sin(A/2) = ±√[(1-cos(A))/2]2.余弦函数：cos(A/2) = ±√[(1+cos(A))/2]3.正切函数：tan(A/2) = ±√[(1-cos(A))/(1+cos(A))]六、倒数公式1.正弦函数：csc(A) = 1/sin(A)sec(A) = 1/cos(A)3.正切函数：cot(A) = 1/tan(A)七、和角公式1.正弦函数：sin(A) + sin(B) = 2sin((A+B)/2)cos((A-B)/2)2.余弦函数：cos(A) + cos(B) = 2cos((A+B)/2)cos((A-B)/2)3.正切函数：tan(A) + tan(B) = (sin(A)+sin(B))/(cos(A)+cos(B))【结论】本文对高中三角函数的公式进行了汇总与解析，包括角度与弧度的转换、基本三角函数公式、和差角公式、倍角公式、半角公式、倒数公式和和角公式。

三角函数的图像和性质一、用五点法作正弦函数和余弦函数的简图（描点法）：正弦函数y=sinx ，x ∈[0，2π]的图象中，五个关键点是：(0,0) (2π,1) (,0) (23π,-1) (2,0)余弦函数y=cosx x [0,2]的图像中，五个关键点是：(0,1) (2π,0) (,-1) (23π,0) (2,1)二、正弦函数、余弦函数和正切函数的图象与性质：sin y x = cos y x = tan y x =图象定义域 R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值 当22x k ππ=+时，max 1y =；当22x k ππ=- 时，min 1y =-．当2x k π=时，max 1y =；当2x k ππ=+时，min1y =-．既无最大值也无最小值周期性 2π 2ππ奇偶性奇函数 偶函数 奇函数单调性 在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦上是增函数； 在32,222k k ππππ⎡⎤++⎢⎥⎣⎦上是减函数． 在[]2,2k k πππ-上是增函数； 在[]2,2k k πππ+上是减函数．在,22k k ππππ⎛⎫-+⎪⎝⎭上是增函数．对称性 对称中心(),0k π 对称轴2x k ππ=+对称中心,02k ππ⎛⎫+ ⎪⎝⎭对称轴x k π=对称中心,02k π⎛⎫⎪⎝⎭无对称轴函 数 性 质例作以下函数的简图(1)y=|sinx|，x ∈[0，2π]， (2)y=-cosx ，x ∈[0，2π]例利用正弦函数和余弦函数的图象，求知足以下条件的x 的集合：21sin )1(≥x 21cos )2(≤x3、周期函数概念：关于函数()y f x =，若是存在一个非零常数T ，使适当x 取概念域内的每一个值时，都有：()()f x T f x +=，那么函数()y f x =就叫做周期函数，非零常数T 叫做那个函数的周期。

注意： 周期T 往往是多值的（如sin y x = 2π,4π,…,-2π,-4π,…都是周期）周期T 中最小的正数叫做()y f x =的最小正周期（有些周期函数没有最小正周期）sin y x =, cos y x =的最小正周期为2π （一样称为周期） 正弦函数、余弦函数：ωπ=2T 。

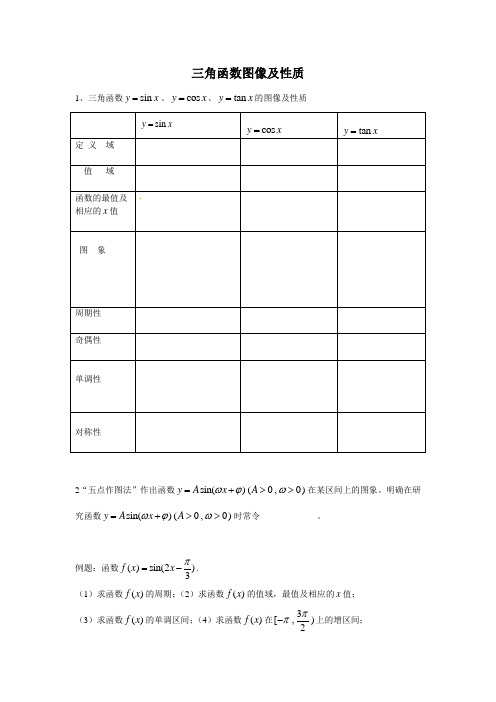
三角函数图像及性质1、三角函数sin y x =、cos y x =、tan y x =的图像及性质2“五点作图法”作出函数sin()(0,0)y A x A ωϕω=+>>在某区间上的图象。

明确在研究函数sin()(0,0)y A x A ωϕω=+>>时常令_____________。

例题：函数()sin(2)3f x x π=-.（1）求函数()f x 的周期；（2）求函数()f x 的值域，最值及相应的x 值； （3）求函数()f x 的单调区间；（4）求函数()f x 在3[,)2ππ-上的增区间；（5）当[0,]2x π∈时，求函数()f x 的取值范围；（6）求函数()f x 的图象的对称中心、对称轴； （7）描述由正弦曲线得到函数()f x 的图象的过程； （8）作出函数()f x 在7[0,)6π上的图象。

3如何求sin()(0,0)y A x A ωϕω=+>>的单调增减区间，对称轴对称中心，最值及取得最值时x 的取值 (1)函数y ＝sin(x ＋4π)在什么区间上是增函数?何时取得最大值？ (2)函数y ＝3sin(3π－2x )在什么区间是减函数? 何时取得最大值？（1）函数y ＝sin （2x ＋25π）图象的对称轴、对称中心的坐标 （2）函数cos(2)2y x π=-图像的对称轴、对称中心(3)函数1tan()24y x π=-的对称中心，单调增区间题型1：周期的应用1、若函数f (x )＝2sin ωx (ω>0)在[－2π3，2π3]上单调递增，则ω的最大值为________．2、若函数f (x )＝2sin ωx (ω>0)在[,]34ππ-上单调递增，则ω的最大值为________3、有一种波，其波形为函数y ＝sin π2x 的图象，若在区间[0，t ]上至少有2个波峰(图象的最高点)，则正整数t 的最小值是________．4、若3sin)(xx f π=，则(1)(2)(3)(2003)f f f f ++++ ＝________。

三角函数的奇偶性与周期性三角函数是数学中重要的函数之一，在数学和物理等领域得到了广泛的应用。

其中，奇偶性与周期性是三角函数的两个重要特征。

本文将对三角函数的奇偶性与周期性进行详细探讨。

一、正弦函数的奇偶性与周期性正弦函数是最基本的三角函数之一，用sin(x)表示。

在单位圆上，正弦函数的值等于对应角度的纵坐标值。

正弦函数具有以下特点：1. 奇偶性：正弦函数是奇函数，即满足sin(-x)=-sin(x)。

这意味着正弦函数关于原点对称，即在原点处取对称轴。

2. 周期性：正弦函数的周期为2π，即在[0,2π]范围内，正弦函数的图像重复出现。

在其他范围内，正弦函数的周期可表示为2π的整数倍。

在图像上，正弦函数的曲线呈现一种波动的形态，无论是在[-2π,2π]范围内还是在其他范围内。

这种周期性的特点使得正弦函数在描述周期性现象时非常有用，如振动、波动等。

二、余弦函数的奇偶性与周期性余弦函数是另一种常见的三角函数，用cos(x)表示。

在单位圆上，余弦函数的值等于对应角度的横坐标值。

余弦函数具有以下特点：1. 奇偶性：余弦函数是偶函数，即满足cos(-x)=cos(x)。

这意味着余弦函数关于y轴对称，即在y轴处取对称轴。

2. 周期性：余弦函数的周期也是2π，与正弦函数相同。

在[0,2π]范围内，余弦函数的图像重复出现。

余弦函数的图像与正弦函数的图像相似，同样呈现一种波动的形态。

但相对于正弦函数，余弦函数的波峰和波谷位置相反，即在同一角度上，正弦函数达到波峰时，余弦函数达到波谷。

三、其他三角函数的性质与周期除了正弦函数和余弦函数，还存在其他几个常见的三角函数，如正切函数、余切函数、正割函数和余割函数。

它们的性质和周期如下：1. 正切函数（tan(x)）：正切函数是奇函数，周期为π。

2. 余切函数（cot(x)）：余切函数是奇函数，周期为π。

3. 正割函数（sec(x)）：正割函数是偶函数，周期为2π。

4. 余割函数（csc(x)）：余割函数是奇函数，周期为2π。

三角函数的周期性与奇偶性三角函数是高中数学中的一个重要部分，它的周期性和奇偶性是在学习三角函数的过程中需要掌握的基本概念。

三角函数中主要包括正弦函数、余弦函数和正切函数。

1. 正弦函数的周期性和奇偶性正弦函数的定义式为y = sin x，其中x为自变量，y为因变量。

正弦函数的图像是一条波形曲线，它的周期为2π，即当x增加一个周期时，y的值会重复一次。

具体来说，正弦函数在[0,2π]区间内的最小正周期为2π。

因此，在对正弦函数进行周期性和奇偶性的分析时，可以把自变量限制在[0,2π]之间。

正弦函数的奇偶性是指当x取反时，y的值是否发生变化。

可以通过正弦函数的定义式来进行验证：sin(-x) = -sin x。

因此，正弦函数是一个奇函数，即在[0,2π]内，正弦函数关于坐标轴的原点对称。

2. 余弦函数的周期性和奇偶性余弦函数的定义式为y = cos x，其中x为自变量，y为因变量。

余弦函数的图像也是一条波形曲线，它的周期也是2π。

与正弦函数类似，余弦函数的最小正周期也为2π。

在对余弦函数进行周期性和奇偶性的分析时，也可以把自变量限制在[0,2π]之间。

余弦函数的奇偶性是指当x取反时，y的值是否发生变化。

通过余弦函数的定义式可以得知：cos(-x) = cos x。

因此，余弦函数是一个偶函数，即在[0,2π]内，余弦函数关于y轴对称。

3. 正切函数的周期性和奇偶性正切函数的定义式为y = tan x，其中x为自变量，y为因变量。

正切函数在定义域内有无数个周期，其最小正周期为π，即当x增加π时，y的值会重复一次。

因此，在对正切函数进行周期性和奇偶性的分析时，需要考虑其多个周期的情况。

正切函数的奇偶性是指当x取反时，y的值是否发生变化。

通过正切函数的定义式可以得知：tan(-x) = -tan x。

因此，正切函数是一个奇函数，即在其每个周期内，正切函数关于坐标轴的原点对称。

综上所述，三角函数的周期性和奇偶性是其在数学中的重要概念之一。

三角函数的周期性和奇偶性三角函数是数学中重要的函数之一，包括正弦函数、余弦函数、正切函数等。

本文将探讨三角函数的周期性和奇偶性，从而帮助读者更好地理解和应用这些函数。

一、周期性1. 正弦函数的周期性正弦函数的周期是2π（或360°），即f(x) = sin(x)在一个周期内的值与下一个周期内的值相同。

换句话说，正弦函数在每个2π的间隔内会重复自身的图像。

例如，f(0) = sin(0) = 0，f(2π) = sin(2π) = 0，f(4π) = sin(4π) = 0，以此类推。

这种周期性特征使得正弦函数在描述周期性现象时非常有用，比如震荡、波动等。

2. 余弦函数的周期性余弦函数的周期同样是2π（或360°），即f(x) = cos(x)在一个周期内的值与下一个周期内的值相同。

与正弦函数类似，余弦函数也在每个2π的间隔内重复自身的图像。

例如，f(0) = cos(0) = 1，f(2π) = cos(2π) = 1，f(4π) = cos(4π) = 1，以此类推。

余弦函数的周期性可以应用于描述周期性运动、振动等现象。

3. 正切函数的周期性正切函数的周期是π（或180°），即f(x) = tan(x)在一个周期内的值与下一个周期内的值相同。

不同于正弦函数和余弦函数，正切函数在每个π的间隔内重复自身的图像。

例如，f(0) = tan(0) = 0，f(π) = tan(π) = 0，f(2π) = tan(2π) = 0，以此类推。

正切函数的周期性可以应用于解决角度相关问题，比如角度变换、角度关系等。

二、奇偶性1. 正弦函数的奇偶性正弦函数的奇偶性体现在函数的对称性上。

具体来说，f(x) = sin(x)是一个奇函数，即f(-x) = -f(x)。

这意味着当自变量的符号取反时，函数值也取反。

例如，f(-π/2) = sin(-π/2) = -1，f(π/2) = sin(π/2) = 1，它们关于y轴对称。

三角函数中的奇偶性与周期性三角函数是数学中非常重要的一类函数，包括正弦函数、余弦函数、正切函数等。

在学习三角函数时，我们会发现它们具有一些特殊的性质，即奇偶性与周期性。

本文将对三角函数中的奇偶性与周期性进行详细的探讨。

一、正弦函数的奇偶性与周期性正弦函数是最基本的三角函数之一，记作sin(x)。

我们来分别讨论正弦函数的奇偶性与周期性。

1. 奇偶性：正弦函数的图像关于y轴对称，即满足f(-x) = -f(x)。

这意味着当x取正值时，正弦函数取相应的正值；当x取负值时，正弦函数取相应的负值。

当x取0时，正弦函数的值为0。

因此，正弦函数是一个奇函数。

2. 周期性：正弦函数的图像在一个周期内重复，一个完整的周期是2π。

也就是说，对于任意实数x，有sin(x + 2π) = sin(x)。

所以正弦函数的周期为2π。

二、余弦函数的奇偶性与周期性余弦函数是三角函数中与正弦函数密切相关的函数，记作cos(x)。

现在我们来研究余弦函数的奇偶性与周期性。

1. 奇偶性：余弦函数的图像关于y轴对称，即满足f(-x) = f(x)。

这意味着当x取正值时，余弦函数取相应的正值；当x取负值时，余弦函数取相应的正值。

当x取0时，余弦函数的值为1。

因此，余弦函数是一个偶函数。

2. 周期性：余弦函数的图像在一个周期内重复，一个完整的周期是2π。

也就是说，对于任意实数x，有cos(x + 2π) = cos(x)。

所以余弦函数的周期为2π。

三、正切函数的奇偶性与周期性正切函数是另一种重要的三角函数，记作tan(x)。

我们来探讨正切函数的奇偶性与周期性。

1. 奇偶性：正切函数不具备奇偶性，即不满足f(-x) = ± f(x)。

也就是说，当x取正值时，正切函数可以是正值或负值；当x取负值时，正切函数也可以是正值或负值。

当x取0时，正切函数的值为0。

因此，正切函数是一个既非奇函数也非偶函数。

2. 周期性：正切函数的图像在一个周期内重复，一个完整的周期是π。

⾼⼀数学三⾓函数基本公式 三⾓函数是⾼中的⼀个重要知识点，是经常要考察的内容，下⾯百分⽹店铺为⼤家整理了⾼⼀数学三⾓函数的基本公式，希望能对⼤家有帮助，更多内容欢迎关注应届毕业⽣⽹！ 公式⼀： 设α为任意⾓，终边相同的⾓的同⼀三⾓函数的值相等： sin（2kπ+α）= sinα cos（2kπ+α）= cosα tan（2kπ+α）= tanα cot（2kπ+α）= cotα 公式⼆： 设α为任意⾓，π+α的三⾓函数值与α的三⾓函数值之间的关系： sin（π+α）= —sinα cos（π+α）= —cosα tan（π+α）= tanα cot（π+α）= cotα 公式三： 任意⾓α与 —α的三⾓函数值之间的关系： sin（—α）= —sinα cos（—α）= cosα tan（—α）= —tanα cot（—α）= —cotα 公式四： 利⽤公式⼆和公式三可以得到π—α与α的三⾓函数值之间的关系： sin（π—α）= sinα cos（π—α）= —cosα tan（π—α）= —tanα cot（π—α）= —cotα 公式五： 利⽤公式—和公式三可以得到2π—α与α的三⾓函数值之间的关系： sin（2π—α）= —sinα cos（2π—α）= cosα tan（2π—α）= —tanα cot（2π—α）= —cotα 公式六： π/2±α及3π/2±α与α的三⾓函数值之间的关系： sin（π/2+α）= cosα cos（π/2+α）= —sinα tan（π/2+α）= —cotα cot（π/2+α）= —tanα sin（π/2—α）= cosα cos（π/2—α）= sinα tan（π/2—α）= cotα cot（π/2—α）= tanα sin（3π/2+α）= —cosα cos（3π/2+α）= sinα tan（3π/2+α）= —cotα cot（3π/2+α）= —tanα sin（3π/2—α）= —cosα cos（3π/2—α）= —sinα tan（3π/2—α）= cotα cot（3π/2—α）= tanα （以上k∈Z） 【拓展】⾼⼀数学三⾓函数的解题思路 第⼀：三⾓函数的重要性，即使你⾼⼀勉强过了，我希望你能在暑假好好学习三⾓函数知识。

三角函数的周期性与奇偶性三角函数是数学中非常重要的一类函数，包括正弦函数sin(x)，余弦函数cos(x)，正切函数tan(x)等。

这些函数在数学、物理、工程等领域中有广泛的应用。

其中，周期性和奇偶性是三角函数的两个重要性质，下面将详细讨论这两个性质。

一、周期性1. 正弦函数sin(x)和余弦函数cos(x)的周期性：正弦函数sin(x)和余弦函数cos(x)都是周期函数，它们的周期都为2π。

也就是说，对于任意实数x，有sin(x+2π) = sin(x)，cos(x+2π) =cos(x)。

这意味着当自变量x增加2π或减少2π时，函数值不变，即函数呈现出周期性的变化规律。

这样的周期性特点使得正弦函数和余弦函数在很多问题中具有重要的意义。

2. 正切函数tan(x)的周期性：正切函数tan(x)也是一个周期函数，它的周期为π。

也就是说，对于任意实数x，有tan(x+π) = tan(x)。

这意味着当自变量x增加π或减少π时，函数值保持不变。

需要注意的是，正切函数在一些特殊点（如π/2，3π/2等）处不定义，因为在这些点上正切函数的值会趋于无穷大，即函数的图像会有垂直渐进线。

二、奇偶性1. 正弦函数sin(x)的奇偶性：正弦函数sin(x)是一个奇函数，它的图像关于原点对称。

也就是说，对于任意实数x，有sin(-x) = -sin(x)。

这意味着当自变量x取相反数时，函数值的相反数与原来的函数值相等，即函数的图像关于y轴对称。

2. 余弦函数cos(x)的奇偶性：余弦函数cos(x)是一个偶函数，它的图像关于y轴对称。

也就是说，对于任意实数x，有cos(-x) = cos(x)。

这意味着当自变量x取相反数时，函数值保持不变，即函数的图像关于y轴对称。

3. 正切函数tan(x)的奇偶性：正切函数tan(x)既不是奇函数也不是偶函数，它的图像既没有关于原点的对称性，也没有关于y轴的对称性。

但是，正切函数有一个特殊的奇偶性质，即tan(-x) = -tan(x)。