清华出版社工程力学答案-第4章 材料力学概述

工程力学（少学时）（第二版）习题册答案第一篇静力学第一章静力学基础知识一、填空：1.机械,运动状态,形状2.牛顿,N3.大小,方向4.矢,带箭头的有向线段,大小,方向,作用点5.形状，大小，保持不变，不存在6.地球，静止，作匀速直线运动7. F或-F , F或-F ,0,08.水平向左,指向右下,垂直向上9.各分力,代数和10.相等,相反,同一直线,两个物体11.相等,相反,同一物体12.二力构件,其两作用点13.矢量14.大小,距离15.力,力臂,逆时针,M O( F ),矩心,N·m 16.相等,相反,平行,力偶臂,力偶作用面17.力的大小,力偶臂,力偶矩, M18.转向,作用面方位二、判断：1.√2.×3.√4.√5.√6.√7.×8.×9.× 10.× 11.× 12.× 13.× 14.√三、选择：1.A2.C3.C4.C5.B6.A7.C8.C9.C 10.C四、简答：1.答：相同点：公理一与公理二中的两个力都是大小相等、方向相反、作用在同一条直线上。

不同点：公理一中的两个力分别作用在两个不同的物体上；公理二中的两个力作用在同一物体上。

2.答:通过B点,由B点指向C点。

因为在主动力F1的作用下, C点的运动趋势方向向上,根据三力平衡汇交定理可知F3的方向是由B点指向C点。

3.答:刚体不会平衡。

因为刚体受两力偶( F1, F1 ')和( F2, F2 ')作用产生顺时针方向转动。

4.答:不对。

力偶矩是由力F '对O点产生的矩平衡的。

5.答:力偶的等效性有: (1)只要保持力偶矩大小和转向不变,力偶可在其作用面内任意移动,而不改变其作用效应。

(2)只要保持力偶矩大小和转向不变,可以同时改变力偶中力的大小和力偶臂的长短,其作用效果不变。

图中d1< d2,若F1×d2= F2×d1,只要F2> F1,丝锥的转动效应会保持不变。

工程力学——课后练习题讲解教师张建平第一章静力学基础课后习题：1. P32习题1-12. P32习题1-23. P33习题1-8图a和b所示分别为正交坐标系Ox解：图（）：F分力：图与解图，两种情形下受力不同，二者的1-2a解图示压路机的碾子可以在推力或拉力作用下滚过）：θ解图第二章力系的简化课后习题：1. P43习题2-12. P43习题2-23. P44习题2-4由作用线处于同一平面内的两个力F和习题图所示一平面力系对A(30)，B(0，图示的结构中，各构件的自重都略去不计。

1图2-4解习题）中的梁∑0,F0,1m习题3-3图解：根据习题3-3第三章附加习题课后习题：1. P69习题3-52. P69习题3-63. P70习题3-74. P71习题3-135. P71习题3-143-14 图示为凸轮顶杆机构，在凸轮上作用有力偶，其力偶矩确定下列结构中螺栓的指定截面Ⅰ－Ⅰ上的内力分量，，产生轴向拉伸变形。

，产生剪切变形。

如习题4-2图所示直杆A、C、B在两端A、B处固定，在C解：首先分析知，该问题属于超静定问题，受力图如图所示：试用截面法计算图示杆件各段的轴力，并画轴力图，单解：(a)题题－3一端固定另一端自由的圆轴承受四个外力偶作用，如5-3解：将轴划分为四个截面扭矩平衡方程im m 扭矩平衡方程+m3-3扭矩平衡方程5-5 试写出图中所示各梁的剪力方程、弯矩方程图3建立坐标系并确定两个控制面，如图左侧为研究对象：−=）取根据力平衡方程和弯矩平衡方程得出4ql弯矩方程：1解建立坐标系，并取两个控制面，如图ql ql1Q。

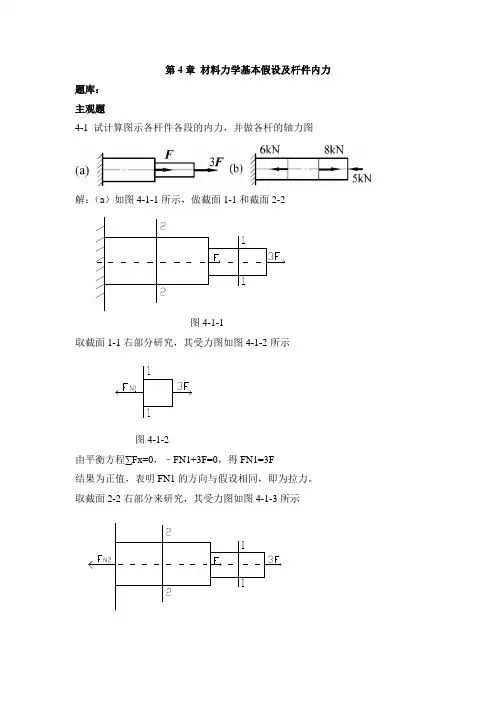
第4章材料力学基本假设及杆件内力题库：主观题4-1 试计算图示各杆件各段的内力，并做各杆的轴力图解：（a）如图4-1-1所示，做截面1-1和截面2-2图4-1-1取截面1-1右部分研究，其受力图如图4-1-2所示图4-1-2由平衡方程∑Fx=0，﹣FN1+3F=0，得FN1=3F结果为正值，表明FN1的方向与假设相同，即为拉力。

取截面2-2右部分来研究，其受力图如图4-1-3所示图4-1-3由平衡方程∑Fx=0，﹣FN2+F+3F=0得FN2=4F结果为正值，表明FN2的方向与假设相同，即为拉力轴力图如图4-1-4所示图4-1-4（b）如图4-1-5所示，做截面1-1、截面2-2和截面3-3图4-1-5取截面1-1右部分来研究，其受力图如图4-1-6所示图4-1-6由平衡方程∑Fx=0，﹣FN1﹣5KN=0，得FN1=-5KN结果为负值，表明FN1的方向与假设相反，即为压力。

取截面2-2右部分来研究，其受力图如图4-1-7所示图4-1-7由平衡方程∑Fx=0，﹣FN2+8KN-5KN=0，得FN2=3KN结果为正值，表明FN2的方向与假设相同，即为拉力。

取截面3-3右部分来研究，其受力图如图4-1-8所示图4-1-8由平衡方程∑Fx=0，﹣FN3﹣6KN+8KN-5KN=0，得FN3=-3KN 结果为负值，表明FN3的方向与假设相反，即为压力。

轴力图如图4-1-9所示：图4-1-9知识点：1．内力，截面法；2. 轴力和轴力图参考页: P72-73学习目标: 2（会用截面法计算法求轴力和轴力图）难度: 1提示一：该题考察知识点：3 内力，截面法；4轴力和轴力图提示二：无提示三：无提示四（同题解）题解：1、用截面法求解每个截面的内力；2、画出每个截面的内力图。

4-2 求图示各梁中指定截面上的剪力和建立图解：（a）计算1-1截面上的剪力Fs和弯矩M1用截面1-1把梁截开，取梁的左段为研究对象如图4-2-1所示图4-2-1由∑Fy=0得：Fs1=-qa（负剪力）由∑Mo1=0得：qa﹒a+M1=0，得M1=-qa2（负弯矩）计算2-2截面上的剪力Fs2和弯矩M2如图4-2-2所示，由∑Fy=0得：Fs2=-qa（负剪力）由∑Mo2=0得M2=-3qa2（负弯矩）图4-2-2计算3-3截面上的剪力Fs3和弯矩M3如图4-2-3所示，由∑Fy=0，-qa-qa-Fs3=0得：Fs3=-2qa（负剪力）由∑Mo3=0，qa﹒4a+qa﹒0.5a+ M3=0得M3=-4.5qa2（负弯矩）图4-2-3（b）计算支座范力选整体梁为研究对象，如图4-2-4所示·图4-2-4由∑MA=0,10KN﹒m+FB×2.5m=0得：FB = -4KN（↓）由∑Fy=0得：FA=-FB=4KN（↑）计算1-1截面上的剪力Fs1和弯矩M1用截面1-1把梁截开，取梁的左段为研究对象如图4-2-5所示图4-2-5由∑Fy=0，FA-Fs1=0,得FA=Fs1=4KN（正剪力）由∑Mo1=0得：-FA·1m+M1=0得M1=4KN·m（正弯矩）计算2-2截面上的剪力Fs2和弯矩M2，如图4-2-6所示图4-2-6由∑Fy=0，FB+Fs2=0,得-FB=Fs2=4KN（正剪力）由∑Mo2=0得：FB·1.5m-M2=0得M2=-6KN·m（负弯矩）（c）计算支座反力选整体梁为研究对象，如图4-2-7所示·图4-2-7由∑Fy=0，FA-5KN+FB=0得FA=3KN（↑）由∑MA=0得：FB·5m-5KN·3m+5KN·m=0得FB=2KN（↑）计算1-1截面上的剪力Fs1和弯矩M1取1-1截面左边部分为研究对象，如图4-2-8所示·图4-2-8由∑Mo1=0得：5KN·m + M1=0，得M1=-5KN·m（负弯矩）由∑Fy=0，FA-Fs1=0,得FA=Fs1=3KN(正剪力)计算2-2的剪力Fs2弯矩M2取2-2截面左边研究对象，如图4-2-9所示·图4-2-9由∑Mo2=0，5KN·m - FA·3m+M2=0，得M2=4KN·m（正弯矩）由∑Fy=0，FA-Fs2=0,得FA=Fs2=3KN(正剪力)计算3-3的剪力Fs3和弯矩M3取3-3截面右边研究对象，如图4-2-10所示图4-2-10由∑Mo3=0，FB·2m-M3=0，得M3=4KN·m（正弯矩）由∑Fy=0，FB+Fs3=0,得-FB=Fs3=-2KN(负剪力)（d）计算支座反力选整体梁为研究对象，如图4-2-11所示图4-2-11由∑MB=0得：qa·25a-FA·2a+qa·a=0,得FA=47qa （↑）由∑Fy=0，FA-2qa+FB=0得FB=41qa （↑）计算1-1截面上的剪力Fs1和弯矩M1取1-1截面左边部分为研究对象，如图4-2-12所示图4-2-12由图知 Fs1=0 M1=0 计算2-2的剪力Fs2弯矩M2取2-2截面左边研究对象，如图4-2-13所示图4-2-13由∑Mo2=0，qa·21a+ M2 =0得M2=-21qa 2（负弯矩）由∑Fy=0，-qa-Fs2=0,得Fs2=-qa(负剪力) 计算3-3的剪力Fs3和弯矩M3取3-3截面右边研究对象，如图4-2-14所示图4-2-14由∑Mo3=0，FB·a-M3=0，得M3=41qa 2（正弯矩）由∑Fy=0，-qa+FB+Fs3=0,得Fs3=43a (正剪力)知识点：1．内力，截面法；2. 轴力和轴力图 参考页: P72-73学习目标: 2（会用截面法计算法求轴力和轴力图） 难度: 1提示一：该题考察知识点：3 内力，截面法；4轴力和轴力图 提示二：无 提示三：无 提示四（同题解） 题解：1、用截面法求解每个截面的内力；2、画出每个截面的内力图。

《工程力学》第4次作业解答（杆件的内力计算与内力图）2008-2009学年第二学期一、填空题1．作用于直杆上的外力（合力）作用线与杆件的轴线重合时，杆只产生沿轴线方向的伸长或缩短变形，这种变形形式称为轴向拉伸或压缩。

2．轴力的大小等于截面截面一侧所有轴向外力的代数和；轴力得正值时，轴力的方向与截面外法线方向相同，杆件受拉伸。

3．杆件受到一对大小相等、转向相反、作用面与轴线垂直的外力偶作用时，杆件任意两相邻横截面产生绕杆轴相对转动，这种变形称为扭转。

4．若传动轴所传递的功率为P 千瓦，转速为n 转/分，则外力偶矩的计算公式为9549P M n=⨯。

5．截面上的扭矩等于该截面一侧（左或右）轴上所有外力偶矩的代数和；扭矩的正负，按右手螺旋法则确定。

6．剪力S F 、弯矩M 与载荷集度q 三者之间的微分关系是()()S dM x F x dx =、()()S dF x q x dx=±。

7．梁上没有均布荷载作用的部分，剪力图为水平直线，弯矩图为斜直线。

8．梁上有均布荷载作用的部分，剪力图为斜直线，弯矩图为抛物线。

9．在集中力作用处，剪力图上有突变，弯矩图上在此处出现转折。

10．梁上集中力偶作用处，剪力图无变化，弯矩图上有突变。

二、问答题1．什么是弹性变形？什么是塑性变形？解答：在外力作用下，构件发生变形，当卸除外力后，构件能够恢复原来的大小和形状，则这种变形称为弹性变形。

如果外力卸除后不能恢复原来的形状和大小，则这种变形称为塑性变形。

2．如图所示，有一直杆，其两端在力F 作用下处于平衡，如果对该杆应用静力学中“力的可传性原理”，可得另外两种受力情况，如图（b ）、（c ）所示。

试问：（1）对于图示的三种受力情况，直杆的变形是否相同？（2）力的可传性原理是否适用于变形体？解答：（1）图示的三种情况，杆件的变形不相同。

图（a ）的杆件整体伸长变形，图（b ）的杆件只有局部伸长变形，图（c ）的杆件是缩短变形。

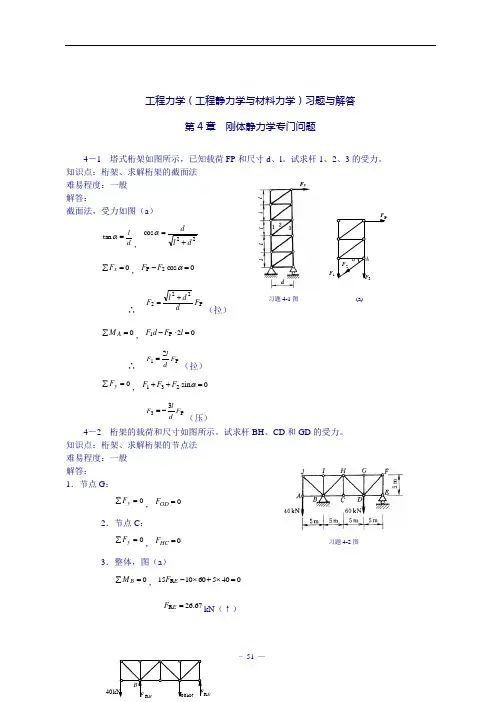
习题4-2图工程力学（工程静力学与材料力学）习题与解答第4章 刚体静力学专门问题4－1 塔式桁架如图所示，已知载荷FP 和尺寸d 、l 。

试求杆1、2、3的受力。

知识点：桁架、求解桁架的截面法 难易程度：一般 解答：截面法，受力如图（a ）d l =αtan ，22cos d l d +=α0=∑x F ，0cos 2P =-αF F∴ P222F d d l F +=（拉）0=∑A M ，02P 1=⋅-l F d F ∴ P 12F d l F =（拉）=∑y F ，0sin 231=++αF F FP 33F d lF -=（压）4－2 桁架的载荷和尺寸如图所示。

试求杆BH 、CD 和GD 的受力。

知识点：桁架、求解桁架的节点法 难易程度：一般 解答：1．节点G ：=∑y F ，0=GD F2．节点C ：=∑y F ，0=HC F3．整体，图（a ）0=∑B M ，0405601015R =⨯+⨯-E F 67.26R =E F kN （↑）习题4-4图习题4-3图4．截面法，图（b ）0=∑H M ，067.26106055=⨯+⨯--CD F 67.6-=CD F kN （压）=∑y F ，067.266022=+--BH F1.47-=BH F kN4－3 试判断图示结构中所有零杆。

知识点：桁架、零杆与零杆的判断 难易程度：一般 解答：由节点C 知，F1 = F4 = 0再由节点E 知，F10 = 0由节点D 知，F7 = 0 由节点B 知，F13 = 0 再由节点A 知，F11 = 04－4 图示桁架的两部分用铰链K 连接，在铰链K 上作用有集中载荷FP = 10kN 。

试求各杆受力。

解：1．由结构和载荷对称性，只需考虑一半桁架即可。

由节点D ，FDF = 0 再由节点F ，FHF = 0再由节点H ，FHJ = 0 再由节点J ，FKJ = FJF = 0 再由节点F ，FFB = 0 2．节点K （图（a ））=∑y F ，030cos 2P =+︒F F KH77.53P -=-=F F KH kN （受压）∴ 77.5-======CA GC KG DB HD KH F F F F F F kN （压）其余各杆受力均为零。

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。

（a）（b）（c）（d）（e）（f）（g）1-2 试画出图示各题中AC杆（带销钉）和BC杆的受力图（a）（b）（c）（a）1-3 画出图中指定物体的受力图。

所有摩擦均不计，各物自重除图中已画出的外均不计。

（a）（b）（c）（d）（e）（f）（g）第二章 平面力系2-1 电动机重P=5000N ，放在水平梁AC 的中央，如图所示。

梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆与水平梁的夹角为30 0。

如忽略撑杆与梁的重量，求绞支座A 、B 处的约束反力。

题2-1图解得: N P F F B A 5000===2-2 物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞车D 上，如图所示。

转动绞车，物体便能升起。

设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为铰链连接。

当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。

题2-2图解得: P F PF AB BC 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线，下垂距离CD =f =1m ，两电线杆间距离AB =40m 。

电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力。

题2-3图以AC 段电线为研究对象，三力汇交2-4 图示为一拔桩装置。

在木桩的点A 上系一绳，将绳的另一端固定在点C ，在绳的点B 系另一绳BE ，将它的另一端固定在点E 。

然后在绳的点D 用力向下拉，并使绳BD 段水平，AB 段铅直；DE 段与水平线、CB 段与铅直线成等角α=0.1rad （弧度）（当α很小时，tan α≈α）。

如向下的拉力F=800N ，求绳AB 作用于桩上的拉力。

题2-4图作BD 两节点的受力图 联合解得：kN F F F A 80100tan 2=≈=α2-5 在四连杆机构ABCD 的铰链B 和C 上分别作用有力F 1和F 2，，机构在图示位置平衡。

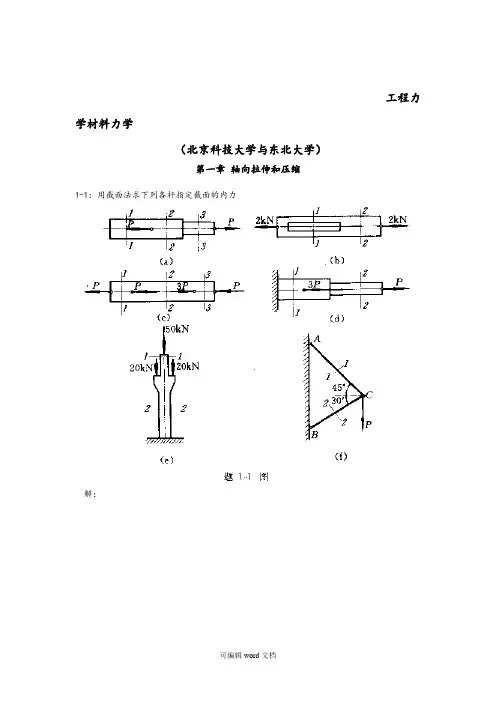
工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。

解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。

解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。

已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。

解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知 材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC AC LNL EA EA σε===1.59*104,CB CB CB LNL EA EA σε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa. 解:NllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。

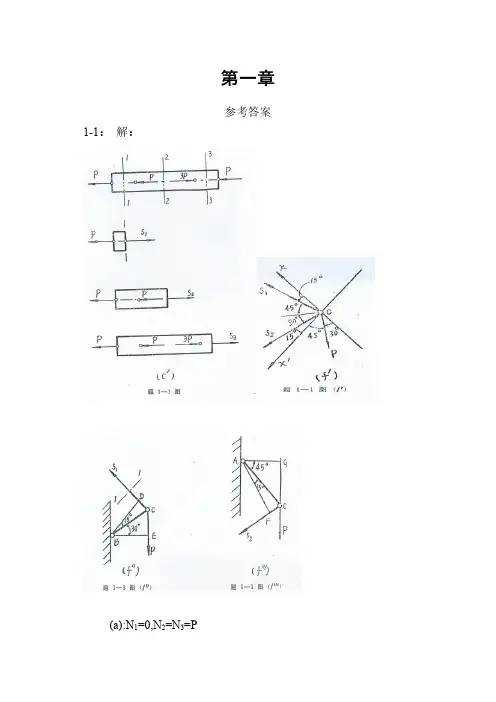
第一章参考答案1-1：解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3=-P(d):N1=-2P,N2=P(e):N1=-50N,N2=-90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2PS =8.72MPa上端双螺孔截面：σ3=3PS =9.15Mpa∴σmax =15.4Mpa1-4：解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5MPa1-5：解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm2∴σmax=2FS =38.1MPa1-6:解:(1)σAC =-20MPa,σCD =0,σDB =-20MPa;△l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2)∴AB l ∆=-0.02mm1-7:解:31.8127AC AC CB CB P MPa S P MPa S σσ====AC AC AC L NL EA EA σε===1.59*104,CB CB CB L NL EA EA σε===6.36*1041-8:解: Nll EAl l ε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：解：208,0.317E GPa ν==1-10：解：[][]max59.5MPa σσ=<1-11：解：（1）当45o α=，[]11.2σσ=>强度不够（2）当60o α=，[]9.17σσ=<强度够1-12：解：[]360,200200200*1013.3100*150*10Y p kNS P kNS MPa A σσ-==∴=====<∑1-13：解：[]max 200213MPa MPaσ=<1-14：解： 1.78, 1.26d cm d cm==拉杆链环1-15解：BC F ==70.7kN70.70.505140F S FS σσ=∴=== 查表得：45*45*31-16解：(1)[]2401601.5s s n σσ===MPa [][]24P S P dσσπ≤∴≤24.4D mm∴=(2)2119.51602P P MPa MPaS d σπ===≤⎛⎫ ⎪⎝⎭1-17解：（1）2*250*6154402D F P A N π⎛⎫=== ⎪⎝⎭78.4AC F MPa S σ==300 3.8378.4s n σσ∴===[][]''''60*3.14*15*1542390F SF S Nσσ===='61544014.521542390F n F ===≈1-18解：P=119kN1-19解：::3:4:535()44AB BC AB BC S P S S P S P =∴==拉，[][][]112841123484AB AB S A kN S P kNP kN σ=====同理所以最大载荷84kN1-20解：P=33.3kN1-21解：71,,12123A B C P F F P F P ===1-22解：10MAX MPaσ=-1-23解：A B X R R R=∴==∑t r l l ∆=∆t AB l l tα∆=21211111223533131.3cd R AC DB CD AC CD CD AF CD MAX Rl Rl l l l l EA EA Rl Rl Rl l EA EA EA EA t EA t R l S MPa A ααασ∆=∆+∆+∆=+=+=∴====第二章习题2-1一螺栓连接如图所示，已知P=200kN ，=2cm ，螺栓材料的许用切应力[τ]=80Mpa，试求螺栓的直径。