初中奥数系列：.图形初步B级.第02讲角.学生版

《角的初步认识》讲义一、角的定义在数学中，角是由两条有公共端点的射线组成的几何图形。

这两条射线叫做角的边，它们的公共端点叫做角的顶点。

比如说，我们常见的三角板，它的每一个角都是由两条边和一个顶点组成的。

角的大小与边的长短无关，而是与两条边张开的程度有关。

两条边张开得越大，角就越大；两条边张开得越小，角就越小。

为了更准确地表示角，我们通常用数字或者三个大写字母来表示。

比如，角 AOB ，其中 O 是顶点，A 和 B 分别是角的两条边所经过的点。

二、角的度量要衡量角的大小，我们需要用到度量工具——量角器。

量角器是一个半圆形的工具，上面标有刻度。

量角的步骤如下：1、把量角器的中心与角的顶点重合。

2、把量角器的零刻度线与角的一条边重合。

3、角的另一条边所对的量角器上的刻度，就是这个角的度数。

需要注意的是，在读角的度数时，要注意是看的内圈刻度还是外圈刻度。

角按照度数的大小可以分为以下几类：1、锐角：小于 90 度的角。

2、直角：等于 90 度的角。

3、钝角：大于 90 度小于 180 度的角。

4、平角：等于 180 度的角。

5、周角：等于 360 度的角。

三、角的画法接下来，我们学习一下如何画角。

1、先画一条射线，作为角的一条边。

2、将量角器的中心与射线的端点重合，零刻度线与射线重合。

3、在量角器上找到要画的角的度数，对应的刻度线的地方点一个点。

4、以射线的端点为端点，通过刚才点的点，再画一条射线，这就是角的另一条边。

四、角在生活中的应用角在我们的日常生活中有着广泛的应用。

比如，我们常见的钟表，时针和分针之间就会形成不同的角。

在整点的时候，时针和分针会形成直角（3 点和 9 点）或者平角（6 点）。

建筑中也常常会用到角的知识。

比如，屋顶的倾斜角度，门窗的开合角度等，都需要精确的设计和计算。

在体育运动中，角也很常见。

比如，足球场上球员射门的角度，篮球运动员投篮的角度等，都会影响比赛的结果。

五、角的相关练习为了更好地掌握角的知识，我们来做一些练习题。

角的初步认识讲课角是我们学习数学的重要概念之一，它在几何学中有着重要的作用。

通过对角的初步认识，我们可以更好地理解和应用它在实际问题中的用途。

本文将介绍角的定义、性质以及常见的角度单位，并结合具体例子来帮助读者更好地理解。

一、角的定义与分类角可以被定义为由两条射线共享一个公共起点所形成的图形。

这个共享的起点称为角的顶点，两条射线则称为角的边。

根据角的大小和形状，我们可以将角分为以下三类：1. 锐角：角度小于90度，尖锐的形状。

2. 直角：角度为90度，形状为一个正方形的内角。

3. 钝角：角度大于90度，形状较为钝圆。

通过对不同种类角的认识，我们可以更好地理解和应用它们在几何学中的特性。

二、角的性质1. 角的度量单位：角的大小可以用度（°）来度量。

一圆周角等于360度，而直角等于90度。

我们可以通过使用度数来测量和记录角的大小。

2. 角的对立角：对于任何角，它的对立角是通过顶点将整个平面分成两个互补的角。

对立角的和总是等于180度。

3. 角的相等性：如果两个角的度数相等，则它们是相等角。

相等角具有相同的大小，无论它们的形状和位置如何。

4. 角的补角和余角：两个角的和等于90度时，这两个角互为补角。

而两个角的和等于180度时，这两个角互为余角。

通过对角的性质的理解，我们可以更加灵活地运用它们来解决实际问题。

三、角度单位的转换在实际问题中，不仅仅使用度数来度量角的大小，还有其他常见的角度单位，如弧度。

1. 弧度：弧度是角度的另一种度量单位。

一圆周角等于2π弧度，而直角等于π/2弧度。

弧度与度之间的转换关系为：180度= π弧度。

2. 角度与弧度的转换：如果要将角度转换为弧度，可以使用以下公式：角度 = 弧度* (180/π)。

反之，如果要将弧度转换为角度，可以使用以下公式：弧度 = 角度* (π/180)。

通过角度单位的转换，我们可以在不同的数学问题中更加方便地进行计算。

综上所述，角的初步认识对于学习几何学和解决实际问题都至关重要。

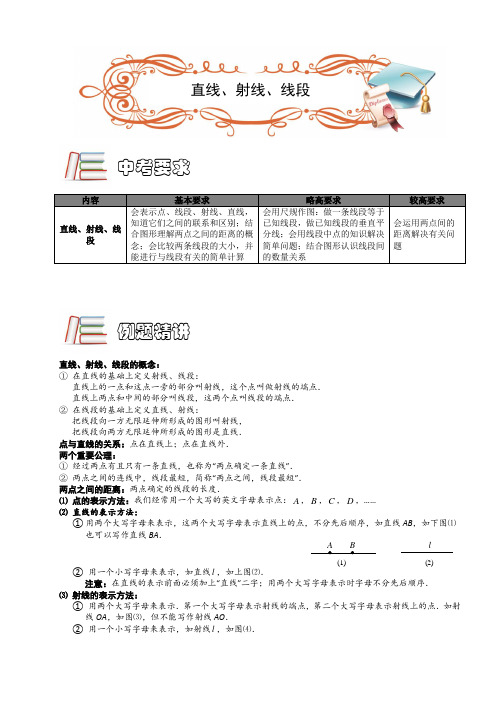
内容 基本要求略高要求较高要求 直线、射线、线段 会表示点、线段、射线、直线，知道它们之间的联系和区别；结合图形理解两点之间的距离的概念；会比较两条线段的大小，并能进行与线段有关的简单计算会用尺规作图：做一条线段等于已知线段，做已知线段的垂直平分线；会用线段中点的知识解决简单问题；结合图形认识线段间的数量关系会运用两点间的距离解决有关问题直线、射线、线段的概念：① 在直线的基础上定义射线、线段：直线上的一点和这点一旁的部分叫射线，这个点叫做射线的端点． 直线上两点和中间的部分叫线段，这两个点叫线段的端点． ② 在线段的基础上定义直线、射线：把线段向一方无限延伸所形成的图形叫射线， 把线段向两方无限延伸所形成的图形是直线． 点与直线的关系：点在直线上；点在直线外． 两个重要公理：① 经过两点有且只有一条直线，也称为“两点确定一条直线”． ② 两点之间的连线中，线段最短，简称“两点之间，线段最短”． 两点之间的距离：两点确定的线段的长度．⑴ 点的表示方法：我们经常用一个大写的英文字母表示点：A ，B ，C ，D ，…… ⑵ 直线的表示方法：① 用两个大写字母来表示，这两个大写字母表示直线上的点，不分先后顺序，如直线AB ，如下图⑴ 也可以写作直线BA ．(1) (2)lA B② 用一个小写字母来表示，如直线l ，如上图⑵．注意：在直线的表示前面必须加上“直线”二字；用两个大写字母表示时字母不分先后顺序． ⑶ 射线的表示方法：① 用两个大写字母来表示．第一个大写字母表示射线的端点，第二个大写字母表示射线上的点．如射线OA ，如图⑶，但不能写作射线AO ．② 用一个小写字母来表示，如射线l ，如图⑷．中考要求例题精讲直线、射线、线段(3) (4)lA O注意：在射线的表示前面必须加上“射线”二字．用两个大写字母表示射线时字母有先后顺序，射线的端点在前．⑷ 线段的表示方法：① 用两个大写字母来表示，这两个大写字母表示线段的两个端点，无先后顺序之分，如线段AB ，如图⑸，也可以写作线段BA ．② 也可以用一个小写字母来表示：如线段l ，如图⑹．(5) (6)AB注意：在线段的表示前面必须加上“线段”二字．用两个大写字母表示线段时字母不分先后顺序．中点：模块一 直线、射线、线段的概念【例1】 下列说法正确的是（ ）A. 直线上一点一旁的部分叫做射线B. 直线是射线的2倍C. 射线AB 与射线BA 是同一条射线D. 过两点P Q 、可画出两条射线【巩固】下列说法中正确的是（ ）A. 直线的一半是射线B. 延长线段AB 至C ，使BC AB =C. 从北京到上海火车行驶的路程就是这两地的距离D. 三条直线两两相交，有三个交点【例2】 下列语句准确规范的是( )A. 直线a b 、相交于一点mB. 延长直线ABC. 反向延长射线AO (O 是端点)D. 延长线段AB 到C ，使BC AB =【巩固】下面说法中错误的是( )A. 直线AB 和直线BA 是同一条直线B. 射线AB 和射线BA 是同一条射线C. 线段AB 和线段BA 是同一条线段D. 把线段AB 向两端无限延伸便得到直线BA【巩固】下列叙述正确的是（ ）A ．孙悟空在天上画一条十万八千里的直线B ．笔直的公路是一条直线C ．点A 一定在直线A B 上D ．过点A 、B 可以画两条不同的直线，分别为直线A B 和直线B A【例3】 根据直线、射线、线段各自的性质，如下图，能够相交的是（ ）D.C.B.B AA.【巩固】下列四个图形中各有一条射线和一条线段，它们能相交的是（ ）C.B.A.【巩固】下列叙述正确的是( )A ．可以画一条长5cm 的直线B ．一根拉紧的线是一条直线C ．直线AB 经过C 点D ．直线AB 与直线BA 是不同的直线【例4】 如图所示根据要求作图：⑴连结AB ；⑵作射线AC ；⑶作直线BC ．ABC模块二 直线公理公理：两点确定一条直线【例5】 如图，图中共有 条线段.EDFCA【巩固】平面上有三个点，经过两点画一条直线，则可以画几条直线?模块三 线段的相关计算【例6】 如图所示，M 是线段A B 的中点，则1______2A M =，2_____2_____A B ==．【巩固】判断：若3c m A BB C ==，则说明B 是A C 的中点．【巩固】判断：已知A ，B ，C 三点在同一条直线上，12AC AB =，那么C 是A B 的中点．【例7】 如图，已知线段AB 上依次有三个点C D E ，，把线段AB 分成2:3:4:5四个部分，56AB =，求BD 的长度.E【巩固】已知14cm AD =，B C ，是AD 上顺次两点，且::2:3:2AB BC CD =，E 为AB 的中点，F 为CD的中点，求EF 的长.E【例8】 如图，已知线段A B 上依次有三个点,,C D E 把线段A B 分成2:3:4:5四个部分，,,,M P Q N 分别是,,,A C C D D E E B的中点，若21,M N =求P Q 的长度. EQDPA【巩固】摄影组从A 市到B 市有一天的路程，计划上午比下午多走100千米到C 市吃饭，由于堵车，中 午才赶到一个小镇，只行驶了原计划的三分之一，过了小镇，汽车赶了400千米，傍晚才停下来休息，司机说，再走从C 市到这里路程的二分之一就到达目的地了，问A B ，两市相距多少千米？模块四 两点之间线段最短【例9】 从家到学校共有条路可以走，如图所示，若想走最近的路，应选择 （填序号）.这是根据 ．学校家【例10】 如图，已知A B ，在直线的两侧，在l 上求一点P ，使PA PB +最小；B l图1【巩固】如图，有一个正方体的盒子1111ABCD A B C D -，在盒子内的顶点A 处有一只蜘蛛，而在对角的顶点1C 处有一只苍蝇。

小升初奥数几何部分教案第一章：几何基础1.1 几何图形概述学习平面几何的基本概念，如点、线、面、角等。

理解并掌握直线、射线、线段的概念及性质。

学习多边形的定义及其性质。

1.2 角的性质角的分类：锐角、直角、钝角、平角、周角。

角的度量：度、分、秒的换算。

邻补角、对顶角、补角、余角的概念及性质。

第二章：三角形2.1 三角形的分类等边三角形、等腰三角形、普通三角形的定义及性质。

理解全等三角形的概念及判定方法。

2.2 三角形的角边关系内角和定理：三角形内角和为180度。

外角定理：三角形的外角等于不相邻的两个内角之和。

三角形的中线、高线、角平分线、中垂线的性质。

第三章：四边形3.1 四边形的分类矩形、平行四边形、梯形、菱形、正方形的定义及性质。

理解四边形的不稳定性。

3.2 四边形的角边关系矩形、平行四边形的对边平行且相等。

梯形的上底和下底平行。

菱形的对角线互相垂直平分。

正方形的性质：四边相等，四个角都是直角。

第四章：圆4.1 圆的基本概念圆的定义、圆心、半径、直径。

弧、扇形的定义及性质。

4.2 圆的性质圆的对称性：轴对称和中心对称。

圆周率的概念及计算。

圆的周长、面积的计算公式。

第五章：几何证明5.1 几何证明的基本方法综合法和分析法。

直接证明和反证法。

5.2 几何证明的定理和性质同角三角函数的基本关系。

相似三角形的性质。

平行线的性质：同位角相等、内错角相等、同旁内角互补。

第六章：相似三角形6.1 相似三角形的定义与性质理解相似三角形的概念：对应角相等，对应边成比例。

掌握相似三角形的性质：面积比、边长比、对应角相等。

6.2 相似三角形的应用使用相似三角形解决实际问题，如放大或缩小图形、计算未知边长等。

学习使用相似三角形证明两三角形相似。

第七章：比例线段与三角形7.1 比例线段的概念与性质学习比例线段的概念：线段之间的比例关系。

掌握比例线段的性质：比例线段相等、比例线段成比例。

7.2 利用比例线段解题使用比例线段解决几何问题，如计算未知线段长度、证明线段比例关系等。

角一、本节学习指导本节概念比较多，属于基础知识，只要我们多画图出来观察，还是挺容易理解的。

二、知识要点1、角：有公共端点的两条射线组成的图形叫做角，两条射线的公共端点叫做这个角的顶点，这两条射线叫做这个角的边。

或：角也可以看成是一条射线绕着它的端点旋转而成的。

2、平角和周角：一条射线绕着它的端点旋转，当终边和始边成一条直线时，所形成的角叫做平角，如图6。

终边继续旋转，当它又和始边重合时，所形成的角叫做周角，如图7。

3、角的表示：①用数字表示单独的角，如∠1，∠2，∠3等。

②用小写的希腊字母表示单独的一个角，如∠α，∠β，∠γ，∠θ等。

③用一个大写英文字母表示一个独立（在一个顶点处只有一个角）的角，如∠B，∠C等。

④用三个大写英文字母表示任一个角，如∠BAD，∠BAE，∠CAE等。

注意：用三个大写英文字母表示角时，一定要把顶点字母写在中间，边上的字母写在两侧。

用一副三角板，可以画出15°，30°，45°，60°，75°，90°，105°，120°，135°，150°，165°4、角的度量角的度量有如下规定：把一个平角180等分，每一份就是1度的角，单位是度，用“°”表示，1度记作“1°”，n度记作“n°”。

把1°的角60等分，每一份叫做1分的角，1分记作“1’”。

把1’ 的角60等分，每一份叫做1秒的角，1秒记作“1””。

5、角的性质（1）角的大小与边的长短无关，只与构成角的两条射线的幅度大小有关。

（2）角的大小可以度量，可以比较（3）角可以参与运算。

6、角的平分线【重要】从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线。

如上图，∵OB平分∠AOC∴∠AOB=∠BOC=1/2∠AOC（或者∠AOC=2∠AOB=2∠BOC）7、余角和补角【重要】①如果两个角的和是一个直角，这两个角叫做互为余角，简称互余，其中一个角是另一个角的余角。