解析圆曲线坐标及其放样方法
- 格式:doc
- 大小:19.54 KB
- 文档页数:2





[摘要]在实际的工程应用当中,如果曲线较长,地形变化大,放样曲线的三个主点已不能满足设计和施工的需要,还需要按照一定的桩距,在曲线上测设整桩和加桩。
这个过程称为圆曲线的详细测设。
偏角法是进行圆弧曲线放样的一种最重要的方法。
[关键词]偏角法放样圆弧曲线当路线由一个方向转到另一个方向时,必须用曲线来连接。
曲线的形式较多,其中,圆曲线是最基本的的一种平面曲线。
偏角根据所测右角计算;圆曲线半径R根据地形条件和工程要求选定。
根据偏角和半径,可以计算其他各个元素。
圆曲线的测设分两步进行,先测设曲线上起控制作用的主点;依据主点再测设曲线上每隔一定距离的里程桩,详细地标顶曲线位置。
为了在实地测设圆曲线的主点,需要知道切线长、曲线长及外距,这些元素称为主点测设元素。
一般情况下,当地形变化不大,曲线长度小于40m时,测设曲线的三个主点已经能够满足设计和施工的需要。
如果曲线较长,地形变化大,则除了测定三个主点以外,还需要按照一定的桩距,在曲线上测设整桩和加桩,这个过程称为圆曲线的详细测设。
圆曲线详细测设的方法很多,有极坐标法、直角坐标法、偏角法等。
其中偏角法是最基本、最重要的方法,也是在实际工程中广泛应用的一种方法。
用偏角法测设圆曲线上的细部点是以曲线的起点(或终点)作为测站,计算出测站至曲线上任一细部点的弦线与切线的夹角——弦切角(称为偏角)和弦长或相邻细部点的弦长,据此确定点的位置。
曲线上的细部点即曲线上的里程桩,一般按曲线半径R规定弧长为lo的整桩。
lo一般规定为5m,10m和20m,R越小,lo也越小。
用偏角法测设圆曲线的细部点,因测设距离的方法不同,分为长弦偏角法和短4偏角法两种。
前者测设测站至细部点的距离(长弦),适合于用经纬仪加测距仪(或用全站仪);后者测社设相邻细部点之间的距离(短弦),适合于用经纬仪加钢尺。
在实际的工程实践当中,为了追求美观,为了与当地的环境与自然相协调,为了有一定的美学价值,一些旅游建筑、大型的公共建筑和标志性建筑往往把其外轮廓立面做成圆弧形。


公路圆曲线简易放样方法在高速公路曲线路段施工中,如何既保证平面曲线放样精度又缩短放样时间呢?这是工程技术人员和施工班组经常遇到的问题。
诚然,测量组可以根据施工需要将每20m 中桩和路线边桩放样出来,但由于点多面广任务量大,局部加密桩一般要由现场技术员和施工班组来完成。
这里以永武A6合同段为例,介绍一个圆曲线简易放样方法,可能会给现场技术员和施工班组节省很多宝贵的时间。
永武A6合同段路线全长28.95公里,其中直线段5.11公里,曲线段23.84公里,曲线段占主线总长度的82.3%,如果把互通区匝道统计在内,则曲线所占的比例更大。
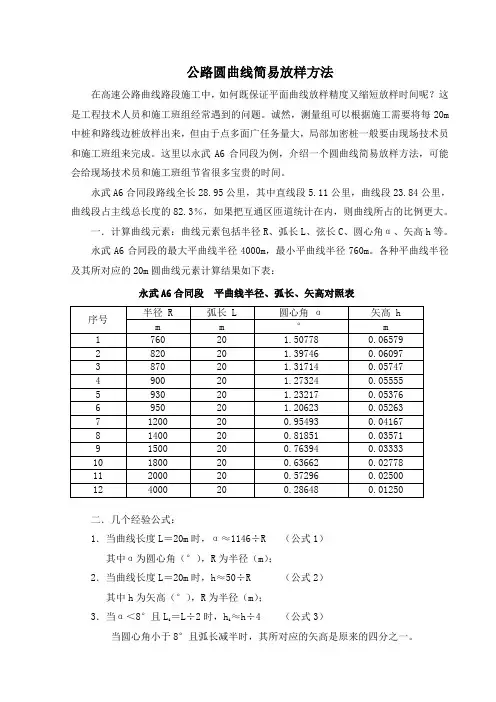
一.计算曲线元素:曲线元素包括半径R、弧长L、弦长C、圆心角α、矢高h等。
永武A6合同段的最大平曲线半径4000m,最小平曲线半径760m。
各种平曲线半径及其所对应的20m圆曲线元素计算结果如下表:永武A6合同段平曲线半径、弧长、矢高对照表二.几个经验公式:1.当曲线长度L=20m时,α≈1146÷R (公式1)其中α为圆心角(°),R为半径(m);2.当曲线长度L=20m时,h≈50÷R (公式2)其中h为矢高(°),R为半径(m);3.当α<8°且Li =L÷2时,hi≈h÷4 (公式3)当圆心角小于8°且弧长减半时,其所对应的矢高是原来的四分之一。
三.准备放样工具:钢尺(50m)1把,测量距离用;尼龙线绳50m以上,挂线用;手锤(2~3p)1把,钉子若干,确定点位用。
四.曲线桩加密方法:举一个路基边沟曲线段加密的例子。
为了简便,放样时以设计半径代替边沟曲线半径。
严格来说,由于边沟位于路基的两侧,其曲线半径与路基中线的曲线半径并不相等,但通过计算可知,20m路段两者矢高之差在0~5mm之间,施工中可以忽略不计。
本人多年前在浆砌边沟施工放样时用加密曲线点的方法逐段缩小矢高数值,当加密到曲线的矢高小于10mm时,边沟外观线形圆滑顺畅,令人满意。



工程测量实验教学指导书(圆曲线放样)课程名称:工程测量学(2)课程编码:66121548学时数;4学时开课单位:资建学院适用专业:测绘BG1、实验课的性质与任务本课程是测绘工程、工程测量的专业课。
本课程的任务是通过教学使学生获得工程测量方面的基本知识、基本理论和基本技能,培养学生分析问题和解决问题的能力,为以后走向工作岗位从事测绘工程奠定重要基础。
2、实验目的与要求2.1工程放样目的;通过放样掌握放样数据计算,放样方法选择,放样精度分析预计以及放样工作设计。
2.2放样数据计算。
要求计算准确,并进行精度预计,写出设计内容。
2.3实地放样。
要求操做认真,培养学生动手能力和分析问题,解决问题能力。
2.4在JD点立仪器,放出T距离,定点ZY。
在曲线起点放样出各点,一直到QZ点重合,并量出闭合差。
2.5每20米一点放样。
3、实验项目及内容提要在实训基地进行。
采用极坐标法放养点位,在两个实训基地进行。
坐标值如下;实验课;曲线放样各组根据自己的选好的已知点可以在操场上放样标出。
放样圆曲线,65人分为12个组,指导教师;顾德元周洪华赵琴霞4、实验报告的格式按学校统一格式5、本课程考核方式、方法及实验成绩评定方法考核方式采取现场考核检查与编写报告相结合方式。
各占50%。
成绩为;优,良,中,及格,不及格:不及格者不允许参加期末考试。
6、实验应配套的主要仪器设备及台(套)数(以一个实验教学班为标准)经纬仪一台,花杆两只,测钎10个,皮尺一个。
以上为每5人一组确定。
7、大纲有关说明实验报告要根据内容调整,不统一。
一个项目一样。
大纲撰写人:顾德元大纲审阅人:负责人:2012年 08月27日。
铁路隧道施工测量——偏角法圆曲线放样摘要测量方法种类繁多,因为坐标法放样应用范围比较广泛,人们应用的也比较多。
在隧道施工测量放样中,由于大多数情况下并不需要放样具体点位,仅需放样出线路中线,偏角法也被广泛应用。
两者各有长短,只有结合使用,才能发挥出最大的工作效率。
关键词铁路隧道测量圆曲线偏角法测量方法种类繁多,因为坐标法放样应用范围比较广泛,人们应用的也比较多。
在隧道施工测量放样中,由于大多数情况下并不需要放样具体点位,仅需放样出线路中线,偏角法也被广泛应用。
1偏角法原理已知圆曲线上A、B两点位置及AB弧长,也知道BC弧长,放样C点位置。
如图1所示:切线切线图1AB6 1=ZBOD=arcsin通过图1不难得出:科技论文一铁路隧道施工测量在圆曲线半径足够大的情况下,我们用弧长代替弦长,即用弧长AB代替线段AB。
皿一,°.弧长AB贝|3 1=ZBOD=arcsin ------2 R同样地,我们可以推出弧长BC6 2=arcsln -------2 R在实际施工放样中,A、B两点是我们事先埋设的导线控制点(在线路中线上),C点是我们需要样的里程的中点,弧长AB变成了A、B两点的里程差,弧长BC变成了8、C两点的里程差。
经纬仪架设于B点,后视A点,如果曲线是右曲线,照准部顺时针拨6= 6 1+ 6 2+180°,如果曲线是左曲线,照准部逆时针拨6= 6 1+ 6 2+180°,仪器望远镜十字划丝即对准C点方向,C点的里程用钢尺拉即可。
2偏角法误差分析在以上原理论述中提到的用弧长代替弦长、用钢尺拉放样位置里程以及要求A、B两点都在曲线中线上都有可能产生误差,误差有多大呢,我们分析一下。
2.1里程代替距离误差分析在上述中,弧长代替弦长前提是半径足够大的情况下,就一般情况来说,产生的误差有多大呢?福厦铁路客运专线一般的曲线半径为4500米,假设后视距离100米,前视距离50米,用46表示偏角误差。
圆曲线放样一:极坐标放样步骤:1.安置经纬仪于ZY 点,瞄准JD1,变换水平读盘读数为: 0°00′00″2.顺时针方向转动照准部,使水平读盘读数为△1,从ZY 点在经纬仪所指方向上用钢尺测设C1,得到P1的位置,用测钎标出;3.再顺时针方向转动照准部,使水平读盘读数为△2,从P1点用钢尺测设弦长C0,与经纬仪所指方向相交,得到P2点的位置,也用测钎标出,以此类推,测设各桩。
4.曲线总长较短时,也可根据经纬仪所指偏角方向,从曲线起点量弦长Ci ,得到点Pi 的位置.测设至圆曲线终,YZ 可作检核;YZ 的偏角应等于α/2,从曲线上最后一点量至YZ 应等于其计算的弦长。
如果两者不符合,其闭合差不应超过如下规定:半径方向(横向):±0.1m 切线方向(纵向)±L/1000 注意事项 :(1)本指导书是根据常规放样方法编写的,放样人员必须根据实际情况,如精度要求、控制点分布、现有仪器、现场条件、计算工具等来选择测站点和放样点的测设方法。
(2)各类工程及同一工程的不同阶段、不同部位对放样点的精度要求不同,所以对测站点和放样点的精度要求也不相同。
(3)作业时要严格执行行业规则和技术规范要求的限差。
如果设计上有特殊要求,要按设计要求执行。
二:偏角法(1)在A 点安置电子经纬仪,照准D 点,转45°对准C 点做校核。
(2)转动照准部,使视线与A 点的切线成1°角( ф=2°),存视线方向上用钢尺量出弦长a ,即可得m 第一点1。
(3)转动照准部,使视线与A 点的切线成2°角,在视线方向上用钢尺量出弦长得出第二点2,同时由l 点量取a ,使其终点落在视线的方向线上进行校核。
(4)用同样的方法放样其他各点,至c 点做校核。
(5)同理,在BJ 安置电子经纬仪,放样另外半圆。
三:弦线支距法⑴ 曲中法:以曲中为原点,弦线O-YZ 为X 轴的方向,过O 点垂直弦线O-YZ 的直线方向为Y 轴,建立直角坐标系--X 1OY 1坐标系见图3。
-108-中国科技信息2006年第2期 CHINA SCIENCE AND TECHNOLOGY INFORMATION Jan.2006工 程 论 坛在道路工程建设中,经常遇有圆曲线施工放样。
常规的放样法有直角坐标法、偏角法和延长弦线法等,这些方法都要利用事先制好的表格查阅有关数据,然后用测量仪器进行放样。
这样,非技术人员难予掌握,而且容易出现差错,特别是在市政道路工程中,常有障碍物阻挡视线,必须将测量仪器移位,换算角度和尺寸,十分不便。
尤其在复曲线的施工放样时,由于不同圆心、不同半径、不同角度交错在一起,更易发生错误。
本人参加多项市政道路工程的圆曲线施工放样,在实践中总结出一种简易的方法,并应用在龙岩市解放路南、中两地段(街心花园至北环路交叉口),取得良好的效果,特别是在北环路交叉口,由四种不同圆心、不同半径和不同角度的复曲线组成,在放样中更显示了简易法优越性,其使用简单,不易差错,误差在允许范围内,值得推广应用。
曲线施工放样可用歌诀表达,即:圆弧曲线难放样,简易方法帮你忙。
连接首尾为旧弦,量出矢高找中点。
首中再连为新弦,新为旧矢半半长。
依次再接新定点,新旧矢比亦半半。
转弯角度小百二,包你成功不变样。
(注:半半为一半之一半,即1/4)。
在工地放样时,实际操作为(如图):1、A、B、E主点为设计已知点。
用钢卷尺量出AB线的中点D,连DE并延长成OX线,DE为矢高a。
2、找出AE1的中点D1,作垂直平分线并延长成OX1线,取D1E1=a1=1/4・a,从而定出E1点,此点为圆曲线的另一点。
3、找出AE1的中点D2,作垂直平分线并延长成OX2线,取D2E2=a2=1/4・a1,从而定出E2点,此点为圆曲线上的又一点。
4、用同样方法可以定出圆曲线上的其余点,将它们用圆滑曲线连成,即为所要放样的圆曲线。
简易法的要点是后一个矢高值为前一个矢高值的1/4,它的理论推导如下(如图所示):点A、E、B为圆曲线上的主点,R为圆曲线的半径,4α为圆曲线的中心角,弧为欲求的圆曲线。
圆曲线放样方法及步骤
圆曲线放样方法及步骤如下:
1.确定圆曲线的几何参数。
包括曲线起点坐标、曲线终点坐标、曲
线半径和曲线方向。
2.根据圆曲线的几何参数,计算出曲线的圆心坐标。
3.将曲线按等分的方式进行分段。
确定放样点的数量和位置。
4.根据放样点的数量。
计算出每个放样点之间的曲线长度。
5.以曲线起点为原点,建立直角坐标系。
并将仪器安置于圆曲线起
点上,后视JD点,并将水平度盘置于零,拨角∠PB1,在此方向上量取d1,得1点。
6.再拨角∠PB2,钢尺零点对准1点,以d为半径,摆动钢尺到经
纬仪方向线上,得2点。
7.再拨角∠PB3,钢尺零点对准2点,以d为半径,摆动钢尺到经
纬仪方向线上,得3点。
8.依此类推,直到放样完成。
解析圆曲线坐标及其放样方法
圆曲线坐标是一种特殊的几何坐标系,它是由一条曲线经过的坐标点组成的。
圆曲线是几何学中的概念,它是一种更贴近自然环境的曲线形状。
其定义是,某一点到曲线所经过的其它点的距离和曲线上某一点到原点O的距离的乘积,此乘积总是常数。
圆曲线坐标的概念是,只要点所形成的距离可以满足圆曲线坐标的定义,它们就是圆曲线坐标。
因此,可以建立一组具有该坐标定义的点,这些点就构成了一条圆曲线。
二、圆曲线坐标的放样方法
圆曲线放样方法是将圆曲线上的点按照一定的规律分布以得到一个平面、立体的效果的技术方法。
通常,圆曲线放样方法分为两种:一种是空间放样法,另一种是平面放样法。
空间放样法是将圆曲线上的点放置在一个三维空间中,通过空间放样可以将一条圆曲线变成贴近自然环境的曲线形状。
这种放样方法可以得到更加真实的效果。
平面放样法是把圆曲线上的点放置在一个二维平面上,从而组成一个半圆形。
此外,还可以利用软件进行放样,把圆曲线以图像的形式在屏幕上重现出来,从而得到一个真实的效果。
三、应用
圆曲线坐标及其放样方法在工程设计中有着广泛应用。
比如,由于具有平滑曲线的独特特点,它们常常被用来作为管道设计,机械设计和船舶设计等工程设计中的基础几何形状。
此外,它也被用
作绘制几何图形的参数化方案,从而能够方便的计算出几何图形的形状参数,进而更加精确地绘制几何图形。
四、总结
圆曲线坐标及其放样方法可以帮助我们设计出更加平滑的几何图形,从而更加真实地绘制几何图形。
此外,它还被广泛应用于工程设计中,用于管道设计、机械设计和船舶设计等工程设计中的基础几何形状。
综上所述,圆曲线坐标及其放样方法可被广泛应用到几何图形的设计和工程设计以及其它领域。